Повторение учебного материала (10 /1)
|
|
|
201
|
1.Рациональные неравенства.
(урок закрепления знаний и умений)
|
|
|
Решение неравенств, содержащих модуль.
Равносильное преобразование неравенств.
|
Знать: правила и алгоритм решения неравенства, содержащего модуль, определение модуля.
Понимать: роль теоретических знаний в создании и решении математической модели.
|
Основываясь на теоретический материал решать линейные неравенства с одной переменной неравенств, содержащих модуль.
|
1)Аргументировать подходы к выполнению заданий.
2) Обосновывать суждения.
3) Планировать и последовательно выполнять алгоритм при совместной работе.
|
-текущий
-взаимоконтроль
Цель: определение уровня усвоения теоретических знаний
Т. 1
|
|
|
202
|
2.Иррациональные числа.
(урок закрепления знаний и умений и отработка навыков).
|
|
|
Выделение квадрата двучлена из выражения, содержащего иррациональное число
;свойства степени: 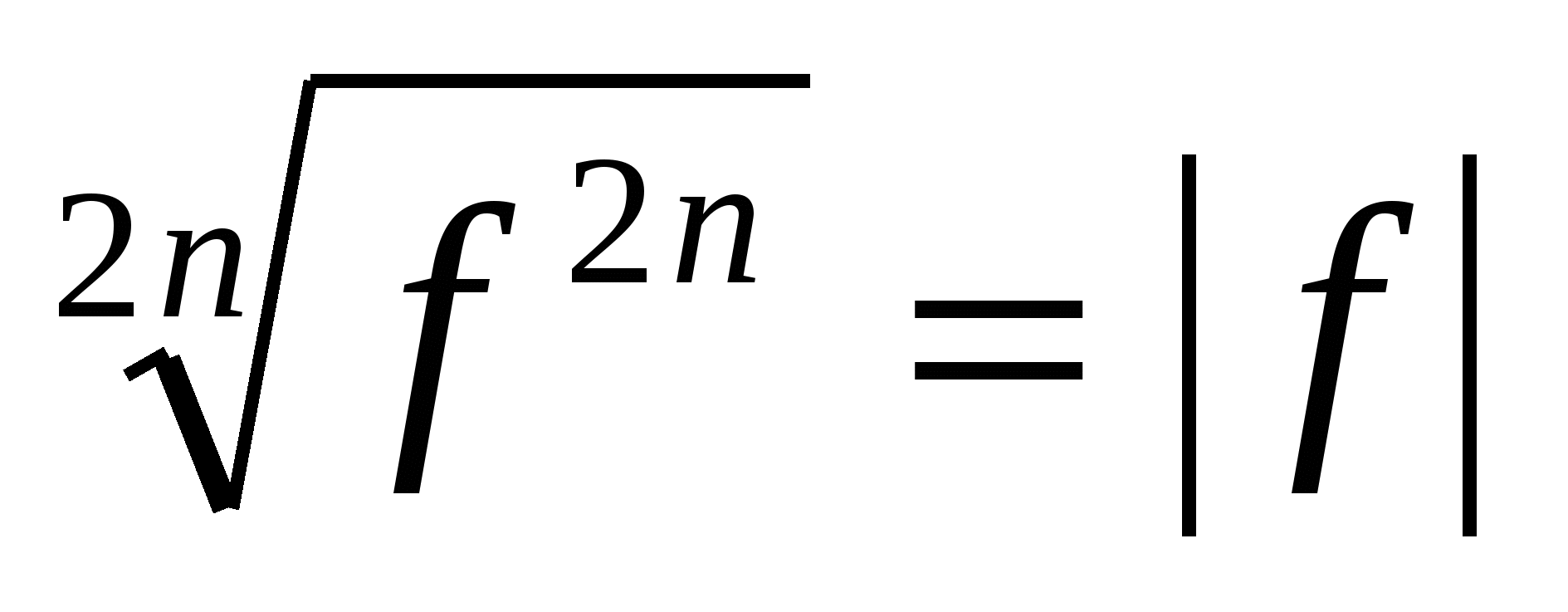
|
Знать: формулы сокращенного умножения; определение числа сопряженного данному.
Понимать: роль полученных ЗУ при нахождении и упрощении выражения, содержащего иррациональные числа.
|
Использовать формулы сокращенного умножения при преобразовании выражений, содержащих иррациональные числа; вести оценку и прикидку значения иррационального выражения.
|
1) Обоснование суждения и конструирование алгоритма решения задач на доказательство.
2) Оценивание необходимости применения изученного материала в практической деятельности и при изучении других предметов.
3) Аргументирование этапов рассуждения.
|
-тематический.
-внешний
Цель: определения уровня усвоения.
С.Р.№3.1
|
|
|
203.
|
3.Модуль действительного числа.
(урок закрепления знаний, умений и отработка навыков).
|
|
|
Определение модуля,
Свойства модуля.
|
Знать: определение и свойства модуля
Понимать: геометрическое изображение аналитической трактовки модуля, действительного числа
|
Применять изученные свойства при нахождении значения иррационального выражения, преобразования выражений, содержащих степень
|
1)Отыскание связи между условием задачи и теоретическим обоснованием
2)Аргументирование и создание аналитической модели решение уравнений и неравенств, содержащих модуль графическим изображением
|
-вводный контроль,
-самоконтроль
Цель: определить уровень ранее (8кл) изученного теоретического материала.
Т. 2
|
|
|
204.
|
4.Свойства функции.
(урок систематизации и обобщения знаний).
|
|
|
Определение изученных свойств функции. Алгоритм исследования функции.
|
Знать: изученные определения; алгоритм исследования функции.
Понимать: использование определений, свойств, при исследовании функции;
возможность графического представления, как средства описания моделей реальных процессов.
|
Использовать полученные знания при исследовании функции по алгоритму;
«читать» графики функций.
|
1) Планирование и осуществление алгоритмической деятельности при построении графиков;
2) Проведение логического обоснования суждений и этапов построения;
3) Проверка и оценка результатов графического представления задания, соотношения их с поставленной задачей.
|
-итоговый
-внешний
Цель: определение уровня ЗУН.
С.Р.№11.2
|
|
|
205.
|
5. Преобразование сумм тригонометрических выражений в произведение.
(урок комплексного применения З.У.Н.)
|
|
|
Изучение формул ;применение формул при доказательстве тождеств; преобразование тригонометрических выражений и нахождение их значений.
|
Знать: формулы.
Понимать: применение изученных формул и перенос знаний в новую нестандартную ситуацию.
(уровень «В2 и «С» в формате ЕГЭ)
|
Применять полученные знания при выполнении практических заданий.
|
1)Отыскание связи между условием задания и изученным теоретическим материалом.
2)Обоснование суждения и конструирование алгоритма решения задач на доказательство.
3) Аргументирование этапов рассуждения.
|
- текущий
- внешний
Цель: определить уровень понимания учебного материала и выявления причинно-следственных связей.
С.Р.№24.3
|
|
|
206.
|
6.Методы решения тригонометрических
уравнений.
(урок систематизации знаний)
(консультация)
|
|
|
Решение уравнений с помощью
преобразования тригонометрических выражений и
универсальных
подстановок.
|
Знать: формулы
преобразования и
методы решения.
Понимать :применение
полученных знаний
при решении
уравнений.
|
Решать уравнения
универсальными
подстановками и с
помощью
изученных формул.
|
. 1)Оценивание необходимости
применения формул в решении
уравнений.
2) Обоснование
суждений в применении
алгоритма доказательства.
|
-текущий
-самоконтроль
Цель: определить
уровень усвоения
учебного
материала.
Т.3
|
|
|
207.
|
7.Вычисление производных.
(урок комплексного применения ЗУН) (практикум)
|
|
|
Правила и формулы при нахождении производных.
|
Знать: основные определения, правила, формулы при нахождении производной функции.
Понимать: роль изученных теоретических знаний в математическом анализе.
|
Находить производные функции, находить скорость изменения функции в точке х=х0 .
|
1)Отыскание связей между теорией и практикой.
2) Выполнение математических действий на основе правил и формул.
3) Умение вести доказательство на основе сравнения, сопоставления и классификации по некоторым критериям.
|
-итоговый
-внешний.
Цель: определить уровень понимания и применения знаний в нестандартных ситуациях.
У.О.
|
|
|
208.
|
8Решение геометрических задач (урок закрепления знаний, умений).
|
|
|
Взаимное расположение прямых и плоскостей в пространстве.
|
Знать: Определение, алгоритм построения.
Понимать: роль правильного выполнения чертежа при решении геометрических задач.
|
Применение полученные теоретические знания при отыскание величин в тетраэдре.
|
1).Развитие абстрактного мышления.
2)Установление причинно- следственных связей по условию задачи
3) Вести доказательство поэтапных рассуждений.
|
итоговый
-внешний.
Цель: определить уровень понимания и применения знаний в нестандартных ситуациях.
|
|
|
209
|
9.Решение геометрических задач (урок закрепления знаний, умений).
|
|
|
Определение тетраэдра, его элементов. Виды тетраэдра (наглядная иллюстрация). Пространственное изображение тетраэдра. Алгоритм построения. Построение сечений.
|
Знать: Определение, алгоритм построения.
Понимать: роль правильного выполнения чертежа при решении геометрических задач.
|
Применение полученные теоретические знания при отыскание величин в тетраэдре.
|
1).Развитие абстрактного мышления.
2)Установление причинно- следственных связей по условию задачи
3) Вести доказательство поэтапных рассуждений.
4)Развитие математической монологической речи.
|
- текущий
- самопроверка
Цель: выявить уровень воспроизведения знаний учащихся
У.О.
|
|
|
210
|
|
|
|
10. Итоговая контрольная работа
|
|
|
 Скачать 2.27 Mb.
Скачать 2.27 Mb.