Тема: «Исследование функции с помощью производной и построение графика»
 Скачать 124.74 Kb. Скачать 124.74 Kb.
|
| Тема: «Исследование функции с помощью производной и построение графика». Цели урока: 1. Образовательная – отработать умения систематизировать, обобщать при исследовании функции ее свойства, применять знания производной при построении графиков функции; 2. Развивающая – развитие мыслительных операций посредством наблюдений, сравнений, сопоставлений, обобщений, развитие зрительной памяти, математической речи учащихся. 3. Воспитательные – воспитание познавательной активности, чувства ответственности, уважения друг другу, взаимопонимания, воспитание культуры общения. Оборудование: презентация, карточки – математическое лото. Тип урока: урок обобщения и систематизации знаний. Ход урока. I.Организационный момент Здравствуйте ребята! Сегодня на уроке мы продолжим изучение применения производной функции для построения графиков различных функций. Так как урок сегодня необычный, то начать я хочу его с необыкновенных слов. «Музыка может возвышать или умиротворять душу, живопись – радовать глаз, поэзия – пробуждать чувства, философия – удовлетворять потребности разума, инженерное дело – совершенствовать материальную сторону жизни людей, а математика способна достичь всех этих целей!» Морис Клайн II. Мотивация
Успешное изучение этой темы поможет вам хорошо сдать государственный экзамен по математике.
А работать мы будем под девизом: « Знания имей отличные, исследуя функции различные». Оценочный лист:
Учащиеся оценивают выполненную ими домашнюю работу. «Кто смолоду делает и думает сам, тот становиться потом, надежнее, крепче, умнее» В. Шукшин. Учащиеся оценивают выполнение ими домашнее задание.
Оцените, пожалуйста, ребята долю своего участия в устной работе. Активно поднимали руку, и вам удалось ответить правильно оценка «5», ваши ответы были правильными, но вы сомневались и стеснялись «4», были неточности «3», вы были пассивны «2».
1. Функция возрастает на [-7; 2) и (2; 8], значит, она возрастает на [-7; 8]. Верно ли? 2. Производная функции в точке х0 равна 0, значит х0 - критическая точка. Верно ли? 3. Производная функции не существует в точке х0, значит х0 - критическая точка. Верно ли? 4. Критическая точка является точкой экстремума. Верно ли? 5. Точка экстремума является критической точкой. Верно ли? Проверка; Проверка, 5 правильных ответов оценка «5», 4-«4», 3-«3», 2-0 оценка «2».
Правильные ответы
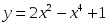 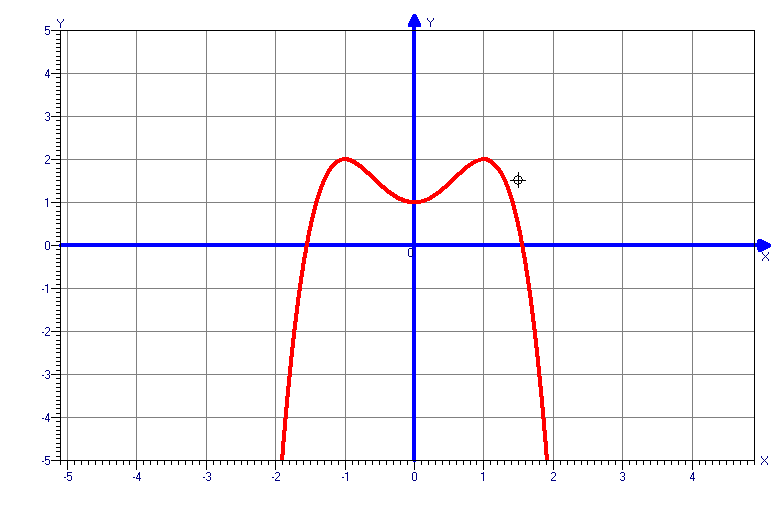 Карточка №1.
Неправильные ответы .
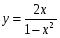 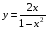 Карточка №2. Карточка №2.
y= f/ ( x) Правильные ответы.
Неправильные ответы
Карточка № 3.
Неправильные ответы .
Правильные ответы
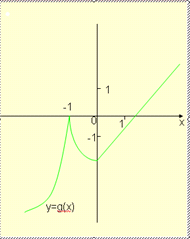 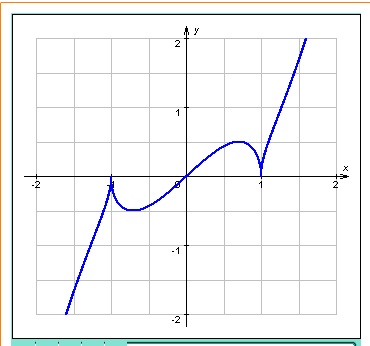 у = f (x)
(Ферма Пьер (1601—1665), французский математик. Математика всегда оставалась для Ферма лишь хобби, и тем не менее он заложил основы многих её областей — аналитической геометрии, исчисления бесконечно малых, дифференциальных уравнений, теории вероятностей). -Кто эти учёные? Слайд 11. Задание: Найти экстремумы функции. 1 группе 1) y = x3 + 6x2 - 15x - 3 2) y = 2х - x² 3) y = x/4 + 9/x 5) y = x – х4/4 7) у = х³-6х²
2 группе 1) y =2 x3 + 3x2 - 12x +5 2) y = 3x² - 4х 3) y = x/4 + 4/x 5) y = 8x – х4/4 7) у = х³+ 3х²
3 группа работает по карточкам-инструкциям
Слайд 12. Первая женщина математик С. В. Ковалевская сказала: « Математик должен быть поэтом в душе». И, следуя ее словам, мы на нашем уроке откроем литературную страничку «Графики функций – пословицы». Подберите к графикам функций, изображенных на слайдах, пословицы, которые раскрывают суть процессов функции: 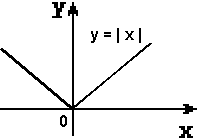 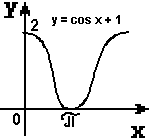 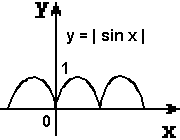 "Как аукнется, так и откликнется". "Повторение - мать учения". "Любишь с горы кататься, люби и саночки возить»
|
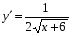
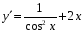
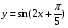
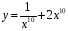
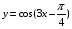
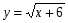
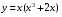
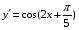
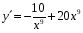
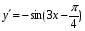
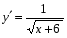
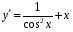

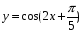
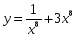
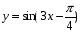
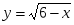
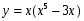
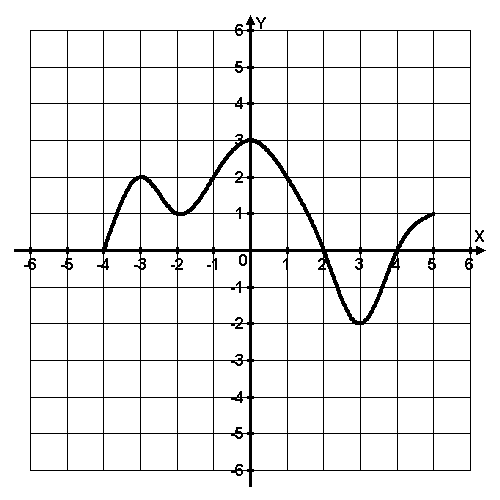
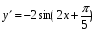
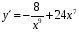
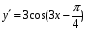
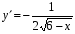
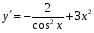
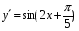
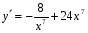
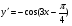
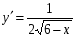
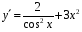
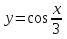
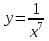 + 4 х 8
+ 4 х 8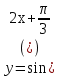
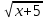
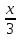
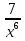 + 4x7
+ 4x7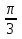 )
)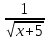
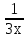 + x
+ x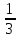 sin
sin 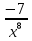 + 32x7
+ 32x7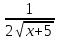
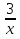 + 1
+ 1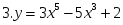
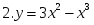
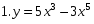 (самопроверка )
(самопроверка )