Элективный курс «Модуль числа. Решение задач, содержащих модуль»
 Скачать 284.36 Kb. Скачать 284.36 Kb.
|
| Управление образования и молодёжной политики администрации Лысковского муниципального района МОУ СОШ №3 г.Лысково Нижегородской области Педагогический проект Элективный курс «Модуль числа. Решение задач, содержащих модуль» Выполнила: учитель математики МОУ СОШ №3 Чехлова О.Ю. г.Лысково 2010 г. СОДЕРЖАНИЕ
1.Аналитико прогностическое обоснование проекта Основная задача обучения математике в школе – обеспечить прочное и сознательное овладение учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену общества, достаточных для изучения смежных дисциплин и продолжения образования. Но программа курса математики в школе не может в полной мере охватить все её разделы. А новая форма итоговой аттестации в форме ЕГЭ требует от учащихся не только знаний на базовом уровне, но и умений выполнять задания повышенной и высокой сложности. Как быть учителю в этой ситуации? На помощь приходят различные формы внеурочной работы с учащимися: ИГЗ, факультативы, кружки, элективные курсы. Ряд тем курса математики средней школы можно более глубоко и детально рассмотреть именно на этих занятиях. При изучении темы «Модуль числа. Уравнения и неравенства, содержащие модуль» в 8 классе у ребят возникали трудности в усвоении понятия модуля, при решении стандартных задач. Так как задания имеют свою специфику, а на изучение темы отводилось лишь 2 учебных часа, то результаты самостоятельных работ показали, что 23% учащихся 8 «А» и 22% учащихся 8 «Б» классов не усвоили материал. (Приложение 1) Учащиеся хотели бы получить более глубокие знания по теме, учитывая, что новая структура экзаменационной работы в форме ЕГЭ так же использует нестандартные задания с модулями, но жесткие рамки программы не дают такой возможности Именно поэтому я взяла для проекта разработку элективного курса по данной теме. Для работы в выбранном направлении имеются все необходимые средства: УМК, дидактические материалы по теме «Модуль числа. Решение задач, содержащих модуль», комплекс ИКТ, время и место для проведения элективного курса. 2.Концепция проекта Успех в современном мире во многом определяется способностью человека организовать свою жизнь как проект: определить дальнюю и ближайшую перспективу, найти и привлечь необходимые ресурсы, наметить план действий и, осуществив его, оценить, удалось ли достичь поставленных целей. Многочисленные исследования, проведенные как в нашей стране, так и за рубежом, показали, что большинство современных лидеров в политике, бизнесе, искусстве, спорте — люди, обладающие проектным типом мышления. Сегодня в школе есть все возможности для развития проектного мышления с помощью особого вида деятельности — проектной деятельности. Педагогический проект представляет собой описание комплекса взаимосвязанных мероприятий, обеспечивающих в течение заданного периода времени создание и распространение или внедрение педагогических новшеств в области содержания образования, образовательных технологий, технологий управления. Образовательной диагностики и т. п. и гарантирующих достижение необходимых эффектов. При этом структура педагогического проекта включает в себя следующие пункты:
Целью данного проекта является разработка элективного курса по теме «Модуль числа. Решение задач, содержащих модуль». Цель определила следующие задачи проекта: - изучить особенности организации элективных курсов в условиях предпрофильной подготовки в 9 классе средней школы; - подобрать необходимый теоретический и дидактический материал по теме «Модуль числа»; - разработать содержание программы элективного курса с учетом индивидуальных способностей и возможностей учащихся, развивая и поддерживая устойчивый интерес к математике. Концепция модернизации российского образования определила основные направления развития отечественной школы. Одним из важнейших шагов на пути к новой школе является введение профильного обучения в старших классах. Предпрофильной подготовкой учащихся основной школы перед предстоящим выбором профилирующего направления собственной деятельности являются элективные курсы по выбору. Элективные курсы – форма учебной работы, состоящая в развитии способностей и интересов учащихся в сочетании с общеобразовательной подготовкой; зарождение интереса к математике на первичном уровне. Целью организации элективных курсов является расширение кругозора учащихся, развитие математического мышления, формирование активного познавательного интереса к предмету, воспитание мировоззрения и ряда личностных качеств средствами углублённого изучения математики. Основная задача элективных курсов: учитывая интересы и склонности учащихся, расширить и углубить знания по предмету, обеспечить усвоение ими программного материала, ознакомить школьников с некоторыми общими идеями современной математики, раскрыть приложения математики на практике. Занятия элективных курсов играют большую роль в совершенствовании школьного, в том числе математического образования. Они позволяют производить поиск и экспериментальную проверку нового содержания, новых методов обучения, в широких пределах варьировать объём сложности изучаемого материала. Программы элективных курсов должны существенно связывать теоретический материал общего характера с приложениями математики, вовлекая в процесс обучения знания, умения, характерные для этапов формирования и интерпретации. Примечательной особенностью элективного курса является то, что программа курса для класса составлена из ряда основных тем, содержание которых непосредственно примыкает к общему курсу математики. Однако содержание учебной работы учащихся на занятиях определяется не только математическим содержанием изучаемых тем и разделов, но и различными методическими факторами:
При выборе методов и приёмов обучения на данных занятиях необходимо учитывать содержание элективного курса, уровень развития и подготовленности учащихся, их интерес к тем или иным разделам программы. Одним из важнейших требований к методам является активизация мышления учащихся, развитие самостоятельности в различных формах её проявления. Элективные курсы могут использоваться разнообразные формы проведения занятий: лекции, практические работы, обсуждение заданий по дополнительной литературе, доклады учеников, составление рефератов, экскурсии. Применение лекционно-семинарской системы при изучении ряда тем курса позволяет излагать учебный материал крупными блоками. При этом важной составляющей занятий является самостоятельная работа учащихся по закреплению и углублению теоретического материала, изложенного на лекции. На практических занятиях проводится целенаправленная работа по выработке у учащихся умений и навыков решения основных типов задач. Семинарские занятия посвящены повторению, углублению и обобщению пройденного материала. По своим дидактическим целям они служат также приобретению новых знаний, обучению самостоятельному применению знаний в нестандартных ситуациях. Полезная форма работы - подготовка рефератов. Выполнение таких заданий важно прежде всего в отношении развития навыков самообразования, удовлетворение индивидуальных интересов учеников. Одновременно индивидуальное задание должно иметь ценность для всех участников группы. Очень большое значение для успешности усвоения материала имеет подбор задач. Хотелось ещё отметить, что занятия должны быть интересными, увлекательными. Хорошо известно, что занимательность изложения помогает раскрытию содержания сложных научных понятий и проблем. Занимательность поможет школьникам освоить элективный курс, содержащиеся в нём идеи и методы математической науки, логику и приёмы творческой деятельности. В этом отношении цель учителя – добиться понимания учениками того, что они подготовлены к работе над сложными проблемами, но для этого необходима заинтересованность предметом, трудолюбие, владение навыками организации своей работы. При организации элективных курсов должны выполняться некоторые общие требования взаимосвязанного построения занятий и уроков по математике:
Учителя и методисты большое значение придают вопросам организации самостоятельной работы на занятиях элективных курсов. Важным фактором для формирования устойчивого интереса учащихся к изучению математики является взаимосвязь (по содержанию) уроков и элективных курсов. Один из эффективных приёмов - это показ новых идей и методов в действии, в применении к задачам, которые “программными” методами решаются гораздо сложнее. Данное условие необходимо для успешного функционирования элективного курса. Причем процесс обучения должен строиться как совместная исследовательская деятельность учащихся — математическая истина (определённое правило, теорема, свойство) не сообщается ученикам “в готовом виде”, а открывается ими самими. Этот процесс начинается с наблюдений, высказывания догадок, суждений о возможном способе решения, о возможном содержании теоремы, правила, после чего следует проверка, поиски дедуктивного обоснования выводов, обобщение, анализ прикладных возможностей. Исследовательская или проблемная структура изучения математики хорошо отвечает развивающим целям обучения элективных курсов. Без определённой подготовки надеяться включить учащихся в успешную многоэтапную творческую поисковую деятельность нереально. Этот успех надо готовить. Для успешного функционирования элективных курсов предусматриваются следующие условия:
Организация математических элективных курсов как осуществление профильной дифференциации даёт возможность всестороннего развития учащихся как личности, как специалистов будущего. Для рассмотрения предлагается элективный курс по теме «Модуль числа. Решение задач, содержащих модуль» Данный элективный курс дает примерный объем знаний, умений и навыков, которым должны овладеть школьники. В этот объем, безусловно, входят те знания, умения и навыки, обязательное приобретение которых предусмотрено требованиями программы общеобразовательной школы: однако предполагается более высокое качество их сформированности. Учащиеся должны научиться решать задачи более высокой по сравнению с обязательным уровнем сложности, овладеть рядом технических и интеллектуальных умений на уровне их свободного использования. Одна из целей преподавания данного курса ориентационная – помочь осознать ученику степень значимости своего интереса к математике и оценить свои возможности, поэтому интерес и склонность учащегося к занятиям на курсах должны всемерно подкрепляться и развиваться. Элективный курс рассчитан на учащихся 9 классов и посвящен систематическому изложению материала, связанного с понятием модуля числа и его применения при решении задач на экзаменах. Материал данного курса содержит «нестандартные» методы, которые позволяют более эффективно решать широкий класс заданий, содержащих модуль, и, безусловно, может использоваться учителем как на занятиях элективного курса, так и на уроках математики в 8-9 классах. Программа курса включает 17 учебных часов. Цели курса: – помочь повысить уровень понимания и практической подготовки в таких вопросах, как: а) преобразование выражений, содержащих модуль; б) решение уравнений и неравенств, содержащих модуль; в) построение графиков элементарных функций, содержащих модуль; – создать в совокупности с основными разделами курса базу для развития способностей учащихся; – помочь осознать степень своего интереса к предмету и оценить возможности овладения им с точки зрения дальнейшей перспективы. Задачи курса: Образовательная: – научить разным методам решения задач, в которых присутствует модуль числа. Развивающая: – развивать умения преодолевать трудности при решении задач разного уровня сложности. Воспитательная: – помочь ученику оценить свой потенциал с точки зрения образовательной перспективы, формировать логическое, абстрактное, эвристическое мышление. Содержание элективного курса
Содержание программы Приложение 2. 3. Стратегия и тактика проектных действий
4. Ожидаемые результаты и способы их оценки В результате изучения курса учащиеся должны уметь: – точно и грамотно формулировать теоретические положения и излагать собственные рассуждения в ходе решения заданий; – применять изученные алгоритмы для решения соответствующих заданий; – преобразовывать выражения, содержащие модуль; – решать уравнения и неравенства, содержащие модуль; – строить графики элементарных функций, содержащих модуль. На занятиях элективного курса развиваются коммуникативные качества обучающихся, чему способствует работа в парах, группах, выступления с докладами, коллективное обсуждение решений. Развивается потребность в самообразовании, совершенствуется самостоятельная работа учащихся. Для успешного анализа и самоанализа определим формы и способы оценки ожидаемых результатов. Динамику можно проследить, используя диагностические работы. (Приложение 3) В результате работы над программой педагог повышает своё профессиональное мастерство, самосовершенствуется и самореализуется. Данная тема может стать основой для продолжения работы, а результаты педагогической деятельности в выбранном направлении могут быть представлены на заседаниях ШМО и РМО. Методические разработки можно использовать не только на факультативных занятиях, но и на уроках. 5. Ресурсная база проекта Для внедрения данного проекта существуют все необходимые ресурсы: - кадровые ресурсы – учитель математики I категории; - информационные – интернет – ресурсы, которые содержат необходимую информацию по данной теме; - материально – технические ресурсы - кабинет математики с необходимым оборудованием; - программно – методические ресурсы представлены следующей литературой:
6. Возможные риски проекта и способы их преодоления Проект полностью реализуется согласно тематическому планированию, которое возможно необходимо будет корректировать в связи с объективными причинами. Так как курс не является обязательным, и учащиеся посещают занятия по своему выбору, то необходимо создать устойчивый интерес к рассматриваемой теме. Опыт показывает, что при выборе элективных курсов занятия математического направления выбирает около 70% учащихся, так как экзамен по математике в 9 классе является обязательным. При этом следует отметить, что требования к знаниям и умениям ни в коем случае не должны быть завышены. Чрезмерность требований порождает перегрузку и ведёт к угасанию интереса. 7. Необходимая поддержка проекта Расходы: - оплата труда учителя руб. - бумага для ксерокса, картридж для копировальной техники, чертежная бумага формата А3 для таблиц, маркеры 1000 руб. Итого руб. Приложение 1. Результаты самостоятельных работ по теме «Модуль числа. Уравнения и неравенства, содержащие модуль» Самостоятельная работа №1.
Результаты самостоятельной работы №1
Самостоятельная работа №2.
Результаты самостоятельной работы № 2.
Приложение 2. Содержание программы 1 тема: Модуль действительного числа. История его происхождения . 2 тема: Основные свойства модуля числа. Геометрический смысл модуля числа. • Основные свойства модуля числа
3 тема: Модуль числа в алгебраических преобразованиях Задания для практики. Упростить выражения  ; ; 4 тема: Решение уравнений вида: │х│= а, │х - b│= а, │f(х)│= а, │f(х)│= g(х) Задания для практики. Решить уравнения
5 тема: Решение уравнений вида│х – b│+ │х – с│= а Задания для практики. Решите уравнения.
5 тема. Урок одной задачи: Решите уравнение 1 способ: ( по определению). Имеем 4 системы по три: 1 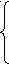 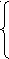 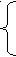 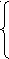 ) х – 3 ≥ 0 х – 3 ≥ 0 х - 3 < 0 х - 3 < 0 ) х – 3 ≥ 0 х – 3 ≥ 0 х - 3 < 0 х - 3 < 0х – 1 ≥ 0 х – 1< 0 х - 1> 0 х - 1< 0 х – 3 – х + 1= 0 х – 3 + х + 1= 0 –х + 3 – х + 1= 0 –х +3 + х - 1= 0  2х = 2 - 2х = - 4 2х = 2 - 2х = - 4 0 = 2 х = 1 х = 2 0 = - 2     • •′ ′ ′ ′ ′ ′ ′ ◦ •′ ′ ′ ′ ′ ′ ′ •′ ′ ′ ′ ◦ ′ ′ ′ ′◦ ◦ • •′ ′ ′ ′ ′ ′ ′ ◦ •′ ′ ′ ′ ′ ′ ′ •′ ′ ′ ′ ◦ ′ ′ ′ ′◦ ◦1 3 х 1 3 х 1 3 х 1 3 х нет решений нет решений х = 2 нет решений Ответ: х = 2.   2 способ: Метод интервалов. 1) х < 1 2) 1 < х < 3 2 способ: Метод интервалов. 1) х < 1 2) 1 < х < 3   3 – х – 1 + х = 0 3 – х – х + 1 = 0 3 – х – 1 + х = 0 3 – х – х + 1 = 0 1 3 0 = - 2 - 2х = - 4  нет решений х = 2 нет решений х = 23) х > 3 х – 3 + 1 - х = 0 -2=0 нет решений Ответ: х = 2. 3 способ: Возведение в квадрат. │х - 3│² =│х - 1│² (х – 3) ² =( х – 1)² х² - 6 х + 9 = х² - 2х + 1 - 4х = - 8 х = 2. Ответ: 2. 4 способ: Способ перебора. 1) 0 ∙ х = 2 2х = 4 нет решений х = 2. 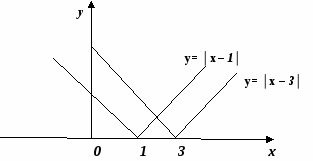 5 способ: Графический. у = │х – 3│ у = │х – 1│ Ответ: 2 Подводя итог занятия, спросить учащихся: Какой способ самый эффективный?; Самый трудный?; Самый простой? Попросить их придумать и решить аналогичные уравнения. 6 тема: Решаем неравенства вида │х │≤ а, │х│≥а Задания для практики. Решите неравенства.
7 тема: Построение множества точек на координатной прямой, плоскости, содержащих знак модуля числа. Задания для практики. Постройте множество точек на координатной плоскости.
8 тема: Построение графиков функций: у=│х│, у= а│х │, у = а│х - m│+b, у = │f( х) │ Задания для практики. Построить графики функций.
9 тема : Итоговое занятие « Математический бой» – соревнование двух команд в решении математических задач. 1.Команды получают условия задач, на решение которых отводится определённое время. При решении задач команда может использовать любую литературу. 2.По истечении времени начинается собственно бой, когда команды рассказывают друг другу решения задач. 3.Одна из команд рассказывает решение, другая выступает в качестве оппонента, т.е. ищет в решении ошибки или недочёты. 4.Выступления оппонента и докладчика оцениваются в баллах жюри (учителя математики, ученики 10, 11 кл.). 5.Победителем боя объявляется команда, которая в итоге наберёт большее количество баллов. Схема боя: 1)Бой состоит из нескольких раундов; 2)Одна из команд вызывает другую; 3) Вызванная команда принимает или не принимает вызов ( 1 минута ); Если принимает, ставит докладчика, вызвавшая команда – оппонента; Если не принимает, то вызывавшая команда выставляет докладчика, а другая оппонента. Происходит проверка корректности вызова. Задания для математического боя: I уровень: 1) Раскрыть модуль: а)│π – 3│, б) │ д) │3² - π²│. 2) Вычислите: а) в) │- 4│∙│- 8│∙│10│:│- 5│, г) (44:│- 11│+│- 3│)∙│ 3) Решите уравнения: а) │х│= 3, б) │у│= 0, в) │а│= - 3, г)│х - 3│= 4, д) │5 - х│= 2, е) │х + 2│= 7, ж) │у + 1│= 0, з) │х - 7│= 2, и) │15 - у│= - 3. 4) Решите неравенства.И изобразите на прямой множества решений: а) │х│> 3, б) │х│≤4, в) │х│≤ 0, д) │х +2│≥ 1. II уровень. 1) Решите уравнения: а)│х² - х - 5│= 1, б)│х² - х - 1│= 1, в) х│х│+ 8х –7 = 0, д) │х² +5 х + 6│= 2, е) х² -│х│ - 2 = 0, ж) │х² - 4х│= 4, з) │х - 3│+│х - 4│=5, и) │х│+│х - 2│+ 2│х- 5│= 6, к) │х - 2│+│х - 4│= 3. 2) Решите неравенство, используя формулу: │х│< а, ( а > 0) <=> - а < х < а. а) │х - а│< 0, б)│2х + 1│≤ - 3, в) │3 - 2х│< х, г) │3х² - 4│≥ х² - 4. 3) Постройте графики функций: а) у = │2х│, б) у = - 2│х│, в) у = - 2│х+ 3│ г) у = - 2│х + 3│- 5, д) у = │х + 1│, е) у = - 3│х - 1│+ 4. Цели, которые должны быть достигнуты при проведении математического боя: • школьники приобретают навыки самостоятельного решения сложных нестандартных задач; • у учащихся формируется умение работать в группе, рассказывать своё решение товарищам, совместно устранять недочёты в решении; • формируются навыки организации групповой работы; • при рассказе решения задачи совершенствуются навыки монологической речи и приобретаются умения видеть и исправлять недочёты своего доклада. • в процессе оппонирования школьники развивают критическое мышление, учатся отличать верные математические утверждения от правдоподобных, но неверных, чётко и лаконично формулировать вопрос. Приложение 3. Диагностическая работа №1 проводится на первом занятии курса. Задача проведения работы: выявление уровня знаний, умений и навыков по теме «Модуль числа» Содержание диагностической работы № 1: 1. Упростить выражение 2. Решить уравнение: │х + 4│= 5. 3. Решить уравнение: 3│х² + 4х + 2│= 5х + 16. 4. Решить неравенство: │2х - 4│≥ 6. 5. Решить неравенство: │3х + 5│< 2, изобразить множество решений на координатной оси. 6. Построить график функции у = 2│х + 2│- 3. Диагностическая работа №2 проводится на третьем занятии 8-ой темы курса. Задача проведения работы: выявление знаний, умений учеников полученных в результате изучения элективного курса. Содержание диагностической работы № 2. 1. Упростите выражение:  . .2. Решите уравнение: │х +4│= 2х – 5. 3. Решите уравнение: │5х² - 10х + 25│= 10х – 5. 4. Решите неравенство: │х - 12│> х +3. 5. Решите неравенство и изобразите множество решений на координатной прямой: 3│х² - 4│≤ 3 6. Построить график функции: у = 2│х - 2│+ 5. 7. Построить график функции: у = ││х │- 3│. Критерии оценки Правильно выполненные и аргументированные решения - 1 балл. Задания, выполненные с ошибкой, но логически верные - 0,5 балла. Не выполненные задания - 0. Уровень знаний оценивается по следующим критериям:
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||