Рабочая программа по математике 5 класс срок реализации программы один год
 Скачать 3.17 Mb. Скачать 3.17 Mb.
|
| Результаты обучения Результаты обучения представлены в Требованиях к результатам обучения и освоения курса математики основной школы и задают систему итоговых результатов обучения, достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Требования распределены по основным содержательным линиям курса и характеризуют тот безусловный минимум, которого должны достигать все учащиеся. Требования к результатам обучения и освоения курса математики основной школы В результате изучения курса математики основной школы ученик должен: знать/понимать
Арифметика уметь:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Алгебра уметь:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, ТЕОРИИ ВЕРОЯТНОСТЕЙ И СТАТИСТИКИ уметь:
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
ГЕОМЕТРИЯ уметь:
использовать приобретённые знания и умения в практической деятельности и повседневной жизни для:
Содержание обучения (алгебра, 9 класс) 1. Свойства функций. Квадратичная функция. Функция. Свойства функций. Квадратный трёхчлен. Разложение квадратного трёхчлена на множители. Функция у = ах2 + bх + с, её свойства и график. Степенная функция. Основная цель: расширить сведения о свойствах функций, ознакомить учащихся со свойствами и графиком квадратичной функции. В начале темы систематизируются сведения о функциях. Повторяются основные понятия: функция, аргумент, область определения функции, график. Даются понятия о возрастании и убывании функции, промежутках знакопостоянства. Тем самым создается база для усвоения свойств квадратичной и степенной функций, а также для дальнейшего углубления функциональных представлений при изучении курса алгебры и начал анализа. Подготовительным шагом к изучению свойств квадратичной функции является также рассмотрение вопроса о квадратном трёхчлене и его корнях, выделении квадрата двучлена из квад ратного трёхчлена, разложении квадратного трёхчлена на множители. Изучение квадратичной функции начинается с рассмотрения функции у=ах2, её свойств и особенностей графика, а также других частных видов квадратичной функции – функций у=ах2+n, у=а(х-m)2. Эти сведения используются при изучении свойств квадратичной функции общего вида. Важно, чтобы обучающиеся поняли, что график функции у = ах2 + bх + с может быть получен из графика функции у = ах2 с помощью двух параллельных переносов. Приёмы построения графика функции у = ах2 + bх + с отрабатываются на конкретных примерах. При этом особое внимание следует уделить формированию у обучающихся умения указывать координаты вершины параболы, ее ось симметрии, направление ветвей параболы. При изучении этой темы дальнейшее развитие получает умение находить по графику промежутки возрастания и убывания функции, а также промежутки, в которых функция сохраняет знак. Учащиеся знакомятся со свойствами степенной функции у=хn при четном и нечетном натуральном показателе n.. Вводится понятие корня n-й степени. Учащиеся должны понимать смысл записей вида 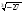 , , 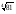 . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется. . Они получают представление о нахождении значений корня с помощью калькулятора, причем выработка соответствующих умений не требуется.2. Уравнения и неравенства с одной переменной. Целые уравнения. Дробные рациональные уравнения. Неравенства второй степени с одной переменной. Метод интервалов. Основная цель: систематизировать и обобщить сведения о решении целых и дробных рациональных уравнений с одной переменной. Сформировать умение решать неравенства вида ах2 + bх + с > 0 или ах2 + bх + с < 0, где а ≠ 0. В этой теме завершается изучение рациональных уравнений с одной переменной. В связи с этим проводится некоторое обобщение и углубление сведений об уравнениях. Вводятся понятия целого рационального уравнения и его степени. Обучающиеся знакомятся с решением уравнений третьей степени и четвертой степени с помощью разложения на множители и введения вспомогательной переменной. Метод решения уравнений путем введения вспомогательных переменных будет широко использоваться в дальнейшем при решении тригонометрических, логарифмических и других видов уравнений. Расширяются сведения о решении дробных рациональных уравнений. Обучающиеся знакомятся с некоторыми специальными приёмами решения таких уравнений. Формирование умений решать неравенства вида ах2 + bх + с >0 или ах2 + bх + с < 0, где а ≠ 0, осуществляется с опорой на сведения о графике квадратичной функции (направление ветвей параболы, её расположение относительно оси Ох). Обучающиеся знакомятся с методом интервалов, с помощью которого решаются несложные рациональные неравенства. 3. Уравнения и неравенства с двумя переменными. Уравнение с двумя переменными и его график. Системы уравнений второй степени. Решение задач с помощью систем уравнений второй степени. Неравенства с двумя переменными и их системы. Основная цель: выработать умение решать простейшие системы, содержащие уравнение второй степени с двумя переменными, и текстовые задачи с помощью составления таких систем. В данной теме завершается изучение систем уравнений с двумя переменными. Основное внимание уделяется системам, в которых одно из уравнений первой степени, а другое второй. Известный учащимся способ подстановки находит здесь дальнейшее применение и позволяет сводить решение таких систем к решению квадратного уравнения. Ознакомление обучающихся с примерами систем уравнений с двумя переменными, в которых оба уравнения второй степени, должно осуществляться с достаточной осторожностью и ограничиваться простейшими примерами. Привлечение известных учащимся графиков позволяет привести примеры графического решения систем уравнений. С помощью графических представлений можно наглядно показать учащимся, что системы двух уравнений с двумя переменными второй степени могут иметь одно, два, три, четыре решения или не иметь решений. Разработанный математический аппарат позволяет существенно расширить класс содержательных текстовых задач, решаемых с помощью систем уравнений. Изучение темы завершается введением понятий неравенства с двумя переменными и системы неравенств с двумя переменными. Сведения о графиках уравнений с двумя переменными используются при иллюстрации множеств решений некоторых простейших неравенств с двумя переменными и их систем. 4. Прогрессии. Арифметическая и геометрическая прогрессии. Формулы n-го члена и суммы первых n членов прогрессии. Бесконечно убывающая геометрическая прогрессия. Основная цель: дать понятия об арифметической и геометрической прогрессиях как числовых последовательностях особого вида. При изучении темы вводится понятие последовательности, разъясняется смысл термина «n-й член последовательности», вырабатывается умение использовать индексное обозначение. Эти сведения носят вспомогательный характер и используются для изучения арифметической и геометрической прогрессий. Работа с формулами n-го члена и суммы первых n членов прогрессий, помимо своего основного назначения, позволяет неоднократно возвращаться к вычислениям, тождественным преобразованиям, решению уравнений, неравенств, систем. Рассматриваются характеристические свойства арифметической и геометрической прогрессий, что позволяет расширить круг предлагаемых задач. 5. Элементы комбинаторики и теории вероятностей. Комбинаторное правило умножения. Перестановки, размеще ния, сочетания. Относительная частота и вероятность случайного события. Основная цель: ознакомить учащихся с понятиями перестановки, размещения, сочетания и соответствующими формулами для подсчета их числа; ввести понятия относительной частоты и вероятности случайного события. Изучение темы начинается с решения задач, в которых требуется составить те или иные комбинации элементов и. подсчитать их число. Разъясняется комбинаторное правило умножения, которое исполнятся в дальнейшем при выводе формул для подсчёта числа перестановок, размещений и сочетаний. При изучении данного материала необходимо обратить внимание обучающихся на различие понятий «размещение» и «сочетание», сформировать у них умение определять, о каком виде комбинаций идет речь в задаче. В данной теме учащиеся знакомятся с начальными сведениями из теории вероятностей. Вводятся понятия «случайное событие», «относительная частота», «вероятность случайного события». Рассматриваются статистический и классический подходы к определению вероятности случайного события. Важно обратить внимание обучающихся на то, что классическое определение вероятности можно применять только к таким моделям реальных событий, в которых все исходы являются равновозможными. 6. Повторение. Основная цель: повторение, обобщение и систематизация знаний, умений и навыков за курс алгебры основной общеобразовательной школы. Содержание обучения (геометрия, 9 класс) 1. Подобие фигур. Понятие о гомотетии и подобии фигур. Подобие треугольников. Признаки подобия треугольников. Подобие прямоугольных треугольников. Центральные и вписанные углы и их свойства. Основная цель: усвоить признаки подобия треугольников и отработать навыки их применения. Данная тема фактически завершает изучение главнейших вопросов курса геометрии: признаки равенства треугольников, сумма углов треугольника, теорема Пифагора. Свойства подобных треугольников будут многократно применяться в дальнейших темах курса, поэтому значительное внимание уделяется решению задач, направленных на формирование умений доказывать подобие треугольников с использованием соответствующих признаков и вычислять элементы подобных треугольников. В данной теме разбирается вопрос об углах, вписанных в окружность. 2. Решение треугольников. Теоремы синусов и косинусов. Решение треугольников. Основная цель: познакомить учащихся с основными алгоритмами решения произвольных треугольников. В данной теме знания учащихся о признаках равенства треугольников, о построении треугольника по трём элементам дополняются сведениями о методах вычисления всех элементов треугольника, если заданы три его определенных элемента. Таким образом обобщаются представления учащихся о том, что любой треугольник может быть задан тремя независимыми элементами. В начале темы доказываются теоремы синусов и косинусов, которые вместе с теоремой о сумме углов треугольника составля ют аппарат решения треугольников. Применение теорем синусов и косинусов закрепляется в решении задач, воспроизведения доказательств этих теорем можно от учащихся не требовать. Среди задач на решение треугольников основными являются три, соответствующие признакам равенства треугольников: решение треугольника по двум сторонам и углу между ними, по стороне и двум углам, по трём сторонам. При их решении в первую очередь следует уделить внимание формированию умений применять теоремы синусов и косинусов для вычисления неизвестных элементов треугольника. Усвоение основных алгоритмов решения произвольных треугольников происходит в ходе решения задач с числовыми данными. При этом широко привлекаются алгебраический аппарат, методы приближенных вычислений, использование тригонометрических таблиц или калькуляторов. Тем самым важные практические умения учащихся получают дальнейшее развитие. 3. Многоугольники. Ломаная. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники. Окружность, вписанная в правильный многоугольник. Окружность, описанная около правильного многоугольника. Длина окружности. Длина дуги окружности. Радианная мера угла. Основная цель: расширить и систематизировать сведения о многоугольниках и окружностях. Сведения о многоугольниках обобщают известные учащимся факты о треугольниках и четырёхугольниках: теорема о сумме углов многоугольника — обобщение теоремы о сумме углов треугольника, равносторонний треугольник и квадрат — частные случаи правильных многоугольников. Изучение формул, связывающих стороны правильных многоугольников с радиусами вписанных в них и описанных около них окружностей, решение задач на вычисление элементов правильных многоугольников, длин окружностей и их дуг подготавливают аппарат решения задач, связанных с многогранниками и телами вращения в стереометрии. Особое внимание следует уделить изучению частных видов многоугольников: правильному треугольнику, квадрату, правильному шестиугольнику. 4. Площади фигур. Площадь и её свойства. Площади прямоугольника, треугольника, параллелограмма, трапеции. Площади круга и его частей. Основная цель: сформировать у учащихся общее представление о площади и умение вычислять площади фигур. Понятие площади и её основные свойства изучаются с опорой на наглядные представления учащихся и их жизненный опыт. В теме доказывается справедливость формулы для вычисления площади прямоугольника, на основе которой выводятся формулы площадей других плоских фигур. Это доказательство от учащихся можно не требовать. Вычисление площадей многоугольников и круга является составной частью решения задач на многогранники и тела вращения в курсе стереометрии. Поэтому при изучении данной темы основное внимание следует уделить формированию практических навыков вычисления площадей плоских фигур в ходе решения соответствующих задач. 5. Элементы стереометрии. Аксиомы стереометрии. Параллельность и перпендикулярность прямых и плоскостей в пространстве. Многогранники. Тела вращения. Основная цель: дать начальное представление о телах и поверхностях в пространстве, о расположении прямых и плоскостей в пространстве. В начале темы дается определение предмета стереометрии, приводится система аксиом стереометрии и пример доказательства с их помощью теорем. Рассматриваются различные случаи расположения прямых и плоскостей в пространстве. Определение простейших многогранников и тел вращения проводится на основе наглядных пред ставлений. 5. Обобщающее повторение курса планиметрии. Основная цель: повторение, обобщение и систематизация знаний, умений и навыков за курс планиметрии 7-9 класса. АЛГЕБРА 9 КЛАСС: 3часа в неделю; всего 102 часа (1 вариант)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||