Рабочая программа по математике 5 класс срок реализации программы один год

Название	Рабочая программа по математике 5 класс срок реализации программы один год
страница	5/18
Дата	05.04.2016
Размер	3.17 Mb.
Тип	Рабочая программа

1 2 3 4 5 6 7 8 9 ... 18

Промежуточная аттестация проводится в форме зачётов и контрольных работ.

Авторское планирование составлено на 34 учебных недели, а базисный учебный план предусматривает 35 учебных недель, поэтому в конце учебного года в раздел повторении добавлено часов из них на алгебру 2 часа и 1 часа на геометрию

Календарно-тематическое планирование составлено на 105 уроков из них 70 часа алгебры и 35 часов геометрии.
УМК

Алгебра, учебник для 8 класса для общеобразовательных учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И.Нешков, С.Б. Суворова : Просвещение, 20011.

Геометрия, 7 – 9. Учебник для общеобразовательных учреждений / Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.: Просвещение, 2009.
Изучение алгебры в 7 – 9 классах. Книга для учителя. / Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение, 2008.
Изучение геометрии в 7 – 9 классах. Методические рекомендации к учебнику. Книга для учителя / Л.С. Атанасян, В.Ф. Бутузов, Ю.А. Глазков: Просвещение, 2004.
Дидактические материалы по алгебре для 8 класса / В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк: Просвещение 2008.
Дидактические материалы по геометрии в8классе. Зив Б.Г. Просвещение 2011год.

Содержание курса
Рациональные дроби

Рациональная дробь. Основное свойство дроби, сокращение дробей. Тождественные преобразования рациональных выражений. Функция у = к/х и ее график.

Понятия дробного выражения, рациональной дроби. Основное свойство дроби. Правило об изменении знака перед дробью. Правила сложения, вычитания дробей с одинаковыми и с разными знаменателями. Правила умножения, деления дробей, возведения дроби в степень. Понятие тождества, тождественно равных выражений, тождественных преобразований выражения. Рациональные выражения и их преобразования. Свойства и график функции

у =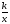

при k > 0; при k < 0.

Четырехугольники . Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции; равнобедренная трапеция

Квадратные корни .

Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближенного значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция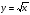

ее свойства и график.

Понятие рационального, иррационального, действительно числа, определение арифметического корня, теоремы о квадратном корне из произведения, из дроби, тождество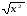

= |x|.

Площадь. Площадь прямоугольника. Площадь параллелограмма, треугольника и трапеции (основные формулы

Теорема Пифагора. Признаки равенства прямоугольных треугольников. Синус, косинус, тангенс, котангенс острого угла прямоугольного треугольника и углов от 0° до 180°; приведение к острому углу. Решение прямоугольных треугольников.

Квадратные уравнения.

Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.

Треугольники. Признаки подобия треугольников.

Соотношения между сторонами и углами прямоугольного треугольника (5 ч). Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Теорема косинусов и теорема синусов; примеры их применения для вычисления элементов треугольника.

Неравенства.

Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.

Окружность. Центр, радиус, диаметр. Дуга, хорда. Центральный, вписанный угол; величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности; равенство касательных, проведенных из одной точки. Метрические соотношения в окружности: свойства секущих, касательных, хорд.

Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные четырехугольники. Вписанные и описанные окружности правильного многоугольника.

Степень с целым показателем. Элементы статистики.

Степень с целым показателем и ее свойства. Стандартный вид числа. Приближенный вычисления.

Повторение.
Требования к математической подготовке учащихся 8 класса
В результате изучения алгебры ученик должен
знать/понимать

существо понятия математического доказательства; примеры доказательств;

существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

уметь
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;

применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами;

нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими

В результате изучения геометрии ученик должен
Уметь объяснить, какая фигура называется многоугольником, назвать его элементы; знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу формулами при исследовании несложных практических ситуаций; суммы углов выпуклого многоугольника и решать задачи типа 364 – 370.

Уметь находить углы многоугольников, их периметры.

Знать определения параллелограмма и трапеции, виды трапеций, формулировки свойств и признаки параллелограмма и равнобедренной трапеции, уметь их

доказывать и применять при решении задач

Уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки; используя свойства параллелограмма и равнобедренной трапеции уметь доказывать некоторые утверждения.

Уметь выполнять задачи на построение четырехугольников.

Знать определения частных видов параллелограмма: прямоугольника, ромба и квадрата, формулировки их свойств и признаков.

Уметь доказывать изученные теоремы и применять их при решении задач типа 401 – 415.

Знать определения симметричных точек и фигур относительно прямой и точки.

Уметь строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.

Знать основные свойства площадей и формулу для вычисления площади прямоугольника. Уметь вывести формулу для вычисления площади прямоугольника

Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу, и уметь применять все изученные формулы при решении задач

Уметь применять все изученные формулы при решении задач, в устной форме доказывать теоремы и излагать необходимый теоретический материал.

Знать теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки. Уметь доказывать теоремы и применять их при решении задач

Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника.

Уметь определять подобные треугольники, находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач

Знать признаки подобия треугольников, определение пропорциональных отрезков. Уметь доказывать признаки подобия и применять их при решении задач

Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике.

Уметь доказывать эти теоремы и применять при решении задач, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение

Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30, 45 и 60, метрические соотношения. Уметь доказывать основное тригонометрическое тождество, решать задачи

Уметь применять все изученные формулы, значения синуса, косинуса, тангенса, метрические отношения при решении задач

Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной.

Уметь их доказывать и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.

Знать определение центрального и вписанного углов, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.

Уметь доказывать эти теоремы и применять при решении задач

Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.

Уметь доказывать эти теоремы и применять их при решении задач.

Уметь выполнять построение замечательных точек треугольника.

Знать, какая, окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырехугольников.

Уметь доказывать эти теоремы и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.

Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.

Уметь доказывать эти теоремы и применять при решении задач

Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.

Уметь доказывать эти теоремы и применять их при решении задач.

Уметь выполнять построение замечательных точек треугольника.

Знать определения вектора и равных векторов.

Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному, решать задачи

Знать законы сложения векторов, определение разности двух векторов; знать, какой вектор называется противоположным данному; уметь объяснить, как определяется сумма двух и более векторов; уметь строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов двумя способами.

Знать, какой вектор называется произведением вектора на число, какой отрезок называется средней линией трапеции.

Уметь формулировать свойства умножения вектора на число, формулировать и доказывать теорему о средней линии трапеции.

Календарно тематическое планирование уроков математики в 8классе.

VІІ вид.

Алгебра – 8 класс (2 часа в неделю, всего 70 часа) М.Ю.Макарычев и др.

	№ урока	Наименование разделов и тем.	Кол-во часов	Дата проведения	Примеча- ние
№ По порядку	№ урока	Наименование разделов и тем.	Кол-во часов		Примеча- ние
ГЛАВА I. РАЦИОНАЛЬНЫЕ ДРОБИ. 17
§1. РАЦИОНАЛЬНЫЕ ДРОБИ И ИХ СВОЙСТВА.			3
1	1	Рациональные выражения, п.1.	1
4 5	2 3	Основное свойство дроби. Сокращения дробей, п.2.	2
§2. СУММА И РАЗНОСТЬ ДРОБЕЙ.			4
7	4	Сложение и вычитание дробей с одинаковыми знаменателями, п.3.	1
8 10 11	5 6 7	Сложение и вычитание дробей с разными знаменателями, п.4.	3
13	8	Контрольная работа №1 «Сложение и вычитание рациональных дробей», п.1-4.	1
§3. ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ.			8
14 16	9 10	Умножение дробей. Возведение дроби в степень, п.5.	2
17 18	11 12	Деление дробей, п.6.	2
19 21	13 14	Преобразование рациональных выражений, п.7.	2
22	15	Функция y=k/x и ее график, п.8.	1
24	16	Контрольная работа №3 «Умножение и деление рациональных дробей», п.5-9.	1
ГЛАВА II. КВАДРАТНЫЕ КОРНИ. 15
§4. ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА.			2
25	17	Рациональные числа. п. 10,	1
27	18	Иррациональные числа. п. 11	1
§5. АРИФМЕТИЧЕСКИЙ КВАДРАТНЫЙ КОРЕНЬ.			5
28	19	Квадратные корни. Арифметический квадратный корень, п.12.	1
30 31	20 21	Уравнение x²=а, п.13.	2
33	22	Нахождение приближенных значений квадратного корня, п.14.	1
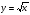34	23	Функция и ее график, п.15.	1
§6. СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ.			3
36 37	24 25	Квадратный корень из произведения и дроби, п.16.	2
39	26	Квадратный корень из степени, п.17.	1
40	27	Контрольная работа №4 «Свойства арифметического квадратного корня», п.10-17.	1
§7. ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ.			3
42	28	Вынесение множителя из-под знака корня. Внесение множителя под знак корня, п.18.	1
43 45	29 30	Преобразование выражений, содержащих квадратные корни, п.19.	2
46	31	Контрольная работа №6 «Преобразование выражений, содержащих квадратные корни», п.18-20.	1
ГЛАВА III. КВАДРАТНЫЕ УРАВНЕНИЯ 13
§8. КВАДРАТНОЕ УРАВНЕНИЕ И ЕГО КОРНИ.			7
48	32	Определение квадратного уравнения. Неполные квадратные уравнения, п.21.	1
49 51	33 34	Формула корней квадратного уравнения, п.22.	2
52 54 55	35 36 37	Решение задач с помощью квадратных уравнений, п.23.	3
57	38	Теорема Виета, п.24.	1
58	39	Контрольная работа №8 «Квадратные уравнения», п.21-24.	1
§9. ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ.			4
60 61 63	40 41 42	Решение дробных рациональных уравнений, п.25.	3
64	43	Решение задач с помощью рациональных уравнений, п.26.	1
66	44	Контрольная работа №9 «Дробные рациональные уравнения», п.25-27.	1
ГЛАВА IV. НЕРАВЕНСТВА. 14
§10. ЧИСЛОВЫЕ НЕРАВЕНСТВА И ИХ СВОЙСТВА.			4
67	45	Числовые неравенства, п..28.	1
69	46	Свойства числовых неравенств, п.29.	1
70	47	Сложение и умножение числовых неравенств, п.30.	1
72	48	Погрешность и точность приближения, п.31.	1
73	49	Контрольная работа №10 «Свойства числовых неравенств», п.28-31.	1
§11. НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ.			8
75	50	Пересечение и объединение множеств, п.32.	1
76	51	Числовые промежутки, п.33.	1
78 80 81	52 53 54	Решение неравенств с одной переменной, п.34.	3
83 84 86	55 56 57	Решение систем неравенств с одной переменной, п.35.	3
87	58	Контрольная работа №13 «Решение неравенств и систем неравенств с одной переменной», п.32-36.	1
ГЛАВА V. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ. ЭЛЕМЕНТЫ СТАТИСТИКИ. 6
§12. СТЕПЕНЬ С ЦЕЛЫМ ПОКАЗАТЕЛЕМ И ЕЕ СВОЙСТВА.			3
89	59	Определение степени с целым отрицательным показателем, п.37.	1
90	60	Свойства степени с целым показателем, п.38.	1
91	61	Стандартный вид числа. п.39.	1
92	62	Контрольная работа №12 «Степень с целым показателем», п.37-39.	1
§13. ЭЛЕМЕНТЫ СТАТИСТИКИ.			2
93	63	Сбор и группировка статистических данных, п.40.	1
96	64	Наглядное представление статистической информации, п.41.	1
ПОВТОРЕНИЕ 5
97	65 66	Квадратные уравнения.	2
99	67	Решение неравенств с одной переменной	1
100	68	Решение неравенств с одной переменной	1
102	69	Итоговый зачёт	1
105	70	Итоговая контрольная работа	1

1 2 3 4 5 6 7 8 9 ... 18