Программа по математикедля 6 класса составлена на основе Программы «Математика. 5-6 классы / авт сост. И. И. Зубарева, А. Г. Мордкович. М. Мнемозина, 2011.»
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
Контрольная работа №1Вариант 1 1. Отметьте на координатной прямой числа: 2; –3,7; 3,5; –1,5. Запишите: а) наибольшее число; б) наименьшее число; в) число, имеющее наибольший модуль; г) число, имеющее наименьший модуль. 2. Запишите число, противоположное данному: а) 0,5; б) –7; в) 0. 3. Запишите x , если: а) –х = 5; б) х = – 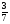 ; в) х = 0. ; в) х = 0.4О. Сравните числа и их модули: а) –5,8 и –0,1; б) – 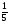 и – и –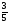 . .5О. Вычислите: а) – 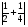 ; б) ; б) 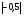 – – 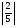 . .Вариант 2 1. Отметьте на координатной прямой числа: –2; 2,5; 3; –4. Запишите: а) наибольшее число; б) наименьшее число; в) число, имеющее наибольший модуль; г) число, имеющее наименьший модуль. 2. Запишите число, противоположное данному: а) –10; б) 0; в) 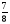 . .3. Запишите x , если: а) х = 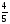 ; б) х = 0; в) –х = –5,2. ; б) х = 0; в) –х = –5,2.4О. Сравните числа и их модули: а) –8,3 и –3,8; б) – 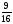 и – и –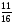 . .5О. Вычислите: а) 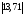 + + 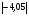 ; б) ; б) 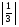 – – 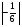 . .Контрольная работа №2Вариант 11. Найдите значение выражения:
2. Вычислите: а) 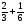 ; б) – ; б) –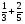 ; в) ; в) 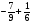 . .3. Найдите значение алгебраической суммы –4,1 + (–8,3) – (–7,3) – (+1,9). 4О. В магазин завезли 700 кг овощей, которые были проданы за 3 дня. В первый день было продано 40% овощей, во второй – 58% остатка. Определите массу овощей, проданных в третий день. 5О. Предприниматель закупил партию сахара, которая была продана за три дня. В первый день было продано 36 ц, что составило 40% всей партии, во второй день – 35% остатка. Определите массу сахара, проданного в третий день. Вариант 21. Найдите значение выражения:
2. Вычислите: а) 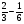 ; б) ; б) 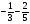 ; в) ; в) 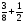 . .3. Найдите значение алгебраической суммы –8,9 + (+18) – (+1,1) – (–12). 4О. Туристический теплоход был в пути три дня. В первый день он прошел 210 км, что составило 35% всего пути, а во второй – 40% оставшегося расстояния. Сколько километров прошел теплоход в третий день? 5О. Предприятием по изготовлению пластиковой тары было изготовлено 5000 бутылок, которые были проданы за три дня. В первый день было продано 30% этого количества, а во второй – 70% остатка. Какое количество бутылок было продано в третий день? Контрольная работа №3Вариант 1 1. Вычислите: а) –0,4 7,1; б) 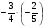 ; в) ; в) 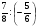 . .2. Отметьте на координатной плоскости точки A(–7;–2), B(2;4), C(1;–5), D(–3;–1). Запишите координаты точки пересечения отрезка AB и прямой CD. 3 О. Найдите значение выражения (2,4 + 0,78) (–0,5) – (8,57 – 19,826) : 2,01. 4О. Дана аналитическая модель числового промежутка: –4 х 3. Постройте его геометрическую модель и составьте соответствующую символическую запись. Вариант 2 1. Вычислите: а) 2,4 (–0,8); б) 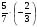 ; в) ; в) 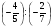 . .2. Отметьте на координатной плоскости точки: A(–5;1), B(5;5), C(–2;8), D(4;–7). Запишите координаты точки пересечения отрезка AB и прямой CD. 3 О. Найдите значение выражения (4,3 – 6,58) 2,5 + (–16,8 + 70,98) : (–8,4). 4О. Дана аналитическая модель числового промежутка: х –4. Постройте его геометрическую модель и составьте соответствующую символическую запись. Контрольная работа №4Вариант 11. Упростите выражение 6(3a – b) – 2(a – 3b). 2. Решите уравнение 10 – 2(3x + 5) = 4(x – 2). 3. В городе два овощных склада. По ошибке на один из них завезли в 4 раза больше картофеля, чем на другой. Чтобы уравнять количество картофеля на обоих складах, пришлось с первого склада перевезти на второй 630 т картофеля. Сколько тонн картофеля было завезено на каждый склад первоначально? 4О. Вычислите: 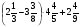 . .5О. Цена яблок – 30 р., а цена груш – 40 р. за 1 кг. а) На сколько процентов груши дороже яблок? б) На сколько процентов яблоки дешевле груш? Вариант 21. Упростите выражение 5(4x – y) – 3(y + 2x). 2. Решите уравнение 7(x – 5) + 1 = 2 – 3(2x –1). 3. В результате ошибки, при комплектовании составов пассажирских поездов один состав оказался в полтора раза длиннее другого. Чтобы уравнять число вагонов в обоих поездах, от первого состава отцепили 4 вагона и прицепили их ко второму составу. Сколько вагонов было в каждом составе первоначально? 4 О. Вычислите: 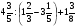 . .5О. Зимние ботинки стоят 2000 р., а осенние 1500 р. а) На сколько процентов зимние ботинки дороже осенних? б) На сколько процентов осенние ботинки дешевле зимних? Контрольная работа №5Вариант 11. Считая, что = 3,14, определите длину окружности и площадь круга, если радиус R = 5 см. 2. Кукурузой занято 84 га, что составляет 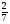 площади всего поля. Определите площадь поля. площади всего поля. Определите площадь поля.3. Площадь поля 84 га, из них 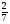 занято картофелем. Определите площадь, занятую картофелем. занято картофелем. Определите площадь, занятую картофелем.4О. В первый день Маша прочитала 36% книги, а во второй 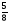 остатка, после чего ей осталось прочитать 48 страниц. Сколько страниц в книге? остатка, после чего ей осталось прочитать 48 страниц. Сколько страниц в книге?5О. Вычислите: 8 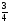 2 2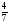 – 10 – 10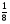 3 3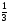 . .Вариант 21. Считая, что = 3,14, определите длину окружности и площадь круга, если радиус R = 7 см. 2. Площадь поля 75 га, из них 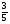 занято картофелем. Определите площадь, занятую картофелем. занято картофелем. Определите площадь, занятую картофелем. 3. Картофелем занято 75 га, что составляет 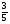 площади всего поля. Определите площадь поля. площади всего поля. Определите площадь поля.4О. За первый месяц со склада было вывезено 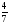 хранившегося там запаса муки, а за второй 15% оставшейся муки, после чего на складе осталось 76.5 т муки. Сколько муки было заложено на хранение на склад? хранившегося там запаса муки, а за второй 15% оставшейся муки, после чего на складе осталось 76.5 т муки. Сколько муки было заложено на хранение на склад?5О. Вычислите: –10 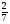 : 1 : 1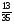 + 3 + 3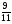 : 1 : 1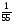 . .Контрольная работа №6Вариант 11. Даны числа 1724, 3965, 7200, 1134. Выберите те из них, которые делятся: а) на 2; б) на 3; в) на 5. 2. Используя признаки делимости, сократите дробь: а) 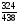 ; б) ; б) 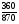 . .3. Можно ли сделать три одинаковых букета из 42 тюльпанов, 21 нарцисса и 6 веточек мимозы? 4О. Найдите частное: 18ab : (6a). 5О. На двух складах хранилось 450 т овощей. После того как с одного склада перевезли на другой 75 т овощей, на втором складе овощей стало в 2 раза больше, чем на первом. Сколько тонн овощей было на каждом складе первоначально? Вариант 21. Даны числа 8141, 3615, 4833, 3240. Выберите те из них, которые делятся: а) на 3; б) на 5; в) на 9. 2. Используя признаки делимости, сократите дробь: а) 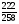 ; б) ; б) 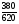 . .3. Имеется 18 карандашей, 36 ручек и 5 блокнотов. Можно ли из них сделать 9 одинаковых наборов? 4О. Найдите частное: 15xy : (5x) 5О. В двух кабинетах было 68 стульев. После того как из одного кабинета в другой перенесли 9 стульев, в первом кабинете стульев оказалось в 3 раза меньше, чем во втором. Сколько стульев было в каждом кабинете первоначально? Контрольная работа №7Вариант 1 1. Разложите на простые множители числа: а) 126; б) 84. 2. Найдите: а) НОД (126; 84); б) НОК(126; 84). 3. Сократите дробь 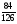 . .4О. Вычислите: 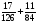 . .5О. Найдите значение выражения 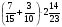 + 1 + 1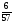 : : 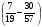 . .Вариант 2 1. Разложите на простые множители числа: а) 105; б) 924. 2. Найдите: а) НОД (105; 924); б) НОК(105; 924). 3. Сократите дробь 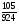 . .4О. Вычислите: 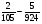 . .5О. Найдите значение выражения 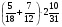 + 1 + 1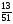 : : 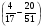 . .Контрольная работа №8Вариант 1 1. Для изготовления сплава взяли золото и серебро в отношении 2 : 3. Определите, сколько килограммов каждого металла в слитке этого сплава массой 7,5 кг. 2. Перед посадкой семена моркови смешивают с песком в отношении 2 : 5. Определите массу семян, если песка потребовалось 200 г. 3. Для изготовления 12 деталей требуется 0,48 кг металла. Сколько деталей можно изготовить из 0,8 кг металла? 4О. Вычислите: 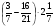 + + 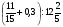 . .5О. Двигаясь со скоростью 64 км/ч, автобус прибыл в пункт назначения через 3,5 ч. На сколько меньше времени ему потребовалось бы на этот путь, если бы он двигался со скоростью 89,6 км/ч? Вариант 2 1. Для изготовления 42 кг земляной смеси использовали песок и чернозем в отношении 2 : 5. Определите массу песка и массу чернозема в этой смеси. 2. Для приготовления опары смешали молоко и муку в отношении 3 : 2. Сколько взяли молока (в килограммах), если муки было взято 5 кг? 3. Расход бензина на 760 км составил 49,4 л. Сколько бензина потребуется на 1140 км? 4О. Вычислите: 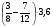 + + 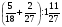 . .5О. 18 самосвалов одинаковой грузоподъемности могут вывезти грунт за 200 поездок. Сколько самосвалов надо добавить, чтобы сократить число поездок до 150? Итоговая контрольная работа за курс 6 класса Вариант 1 1. Вычислите: 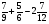 . .2. Выполните действия: 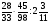 . .3. Упростите выражение 5(3 + 2x) – 2(12 – 8x). 4. В одной цистерне в 4 раза меньше нефти, чем во второй. После того как в первую цистерну добавили 20 т нефти, а из второй откачали 19 т, нефти в обеих цистернах стало поровну. Сколько тонн нефти было в каждой цистерне первоначально? 5. Туристы были в пути 3 дня. В первый день они преодолели 36% всего расстояния, во второй 52% оставшегося, а в третий – 54 км. Найдите длину всего пути. Вариант 2 1. Вычислите: 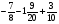 . .2. Выполните действия: 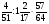 . .3. Упростите выражение –7(6x + 3) – 5(4 – x). 4. На одном складе было в 2,5 раза меньше овощей, чем на второй. После того как на первый склад завезли 180 т овощей, а на второй 60 т, овощей на обоих складах стало поровну. Сколько тонн овощей было на каждом складе первоначально? 5. Поле, площадью 18 га вспахали за 3 дня. В первый день вспахали 35% всего поля, а во второй 40% оставшейся площади. Сколько гектаров вспахали в третий день? Критерии и нормы оценки знаний, умений и навыков обучающихся по математике. 1. Оценка письменных контрольных работ обучающихся по математике. Ответ оценивается отметкой «5», если:
Отметка «4» ставится в следующих случаях:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий. 2. Оценка устных ответов обучающихся по математике. Ответ оценивается отметкой «5», если ученик:
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
Отметка «3» ставится в следующих случаях:
Отметка «2» ставится в следующих случаях:
|