А1. Упростите
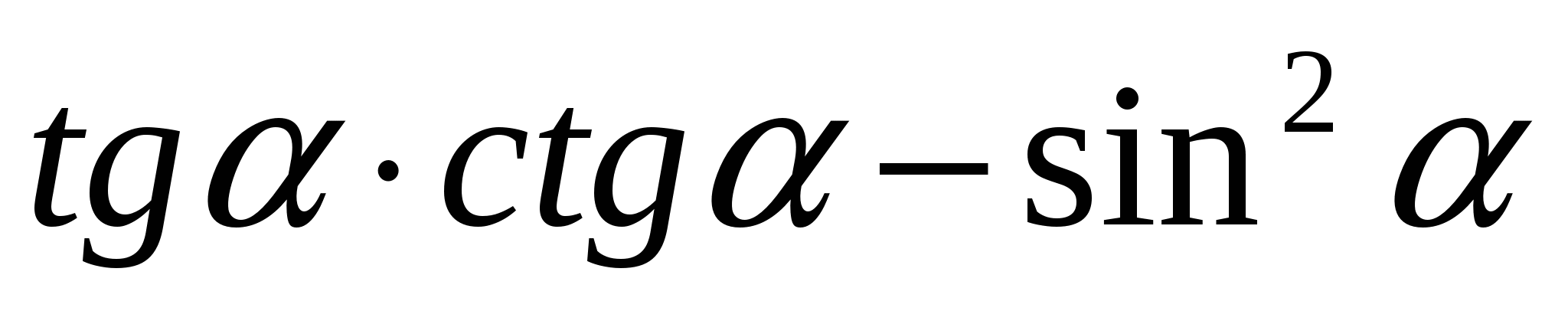
А2. Найдите значение выражения
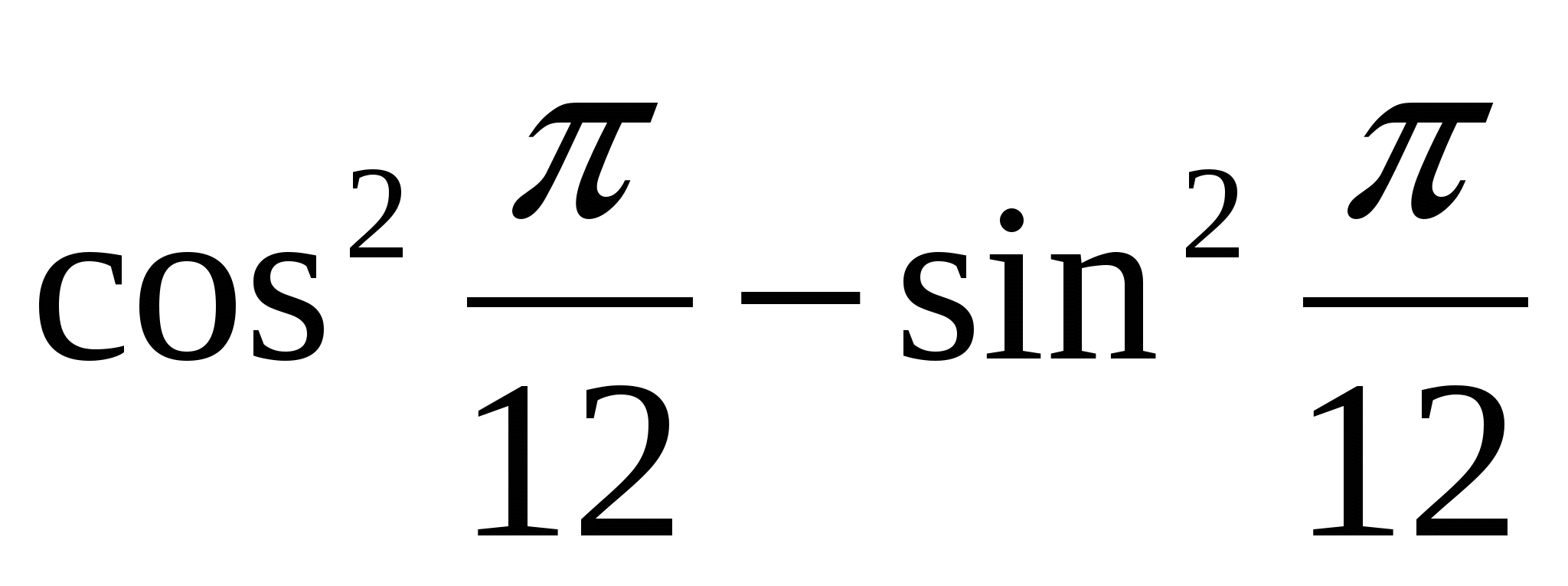
А3. Решить уравнение:
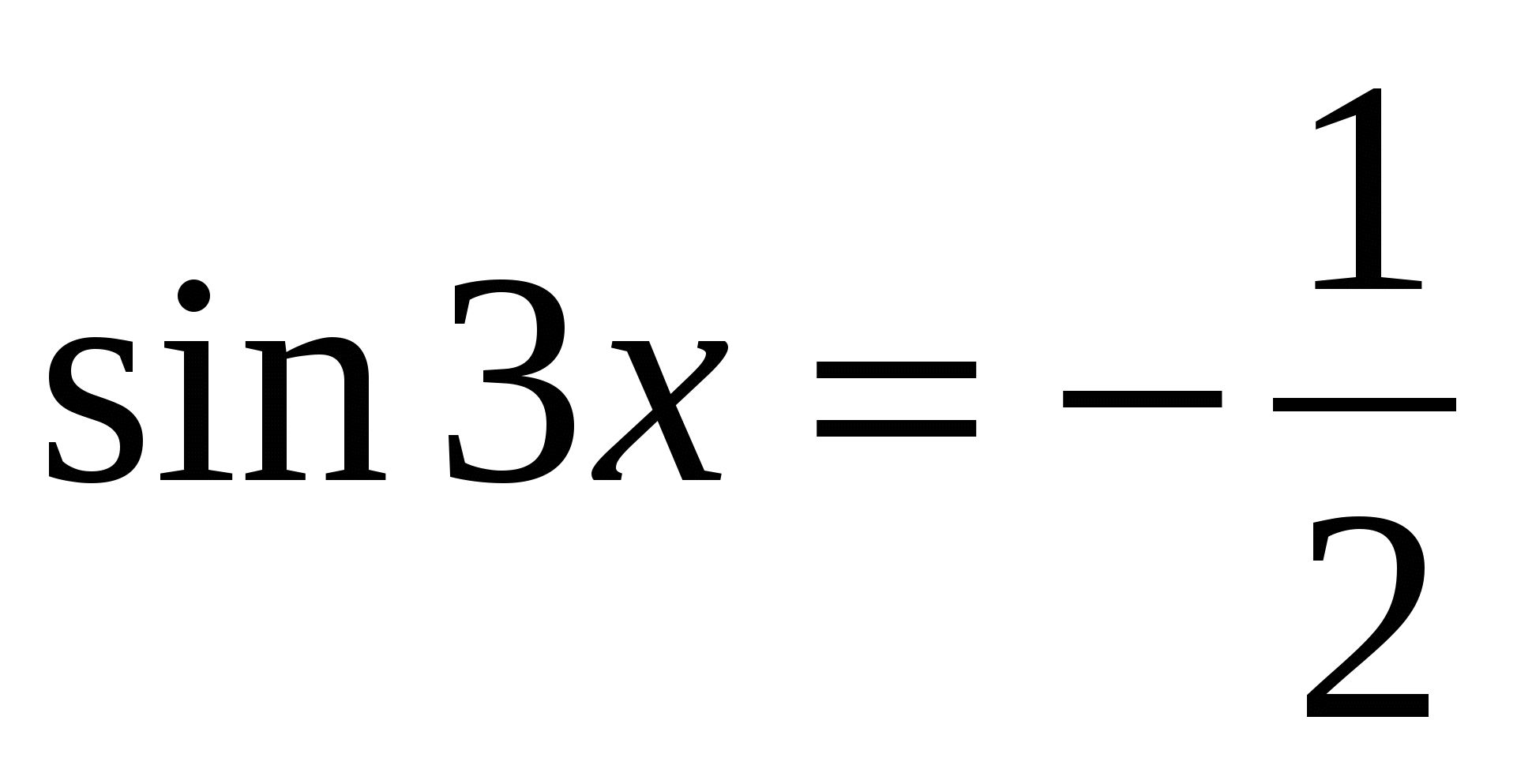
А3. Сколько точек минимума имеет функция на отрезке 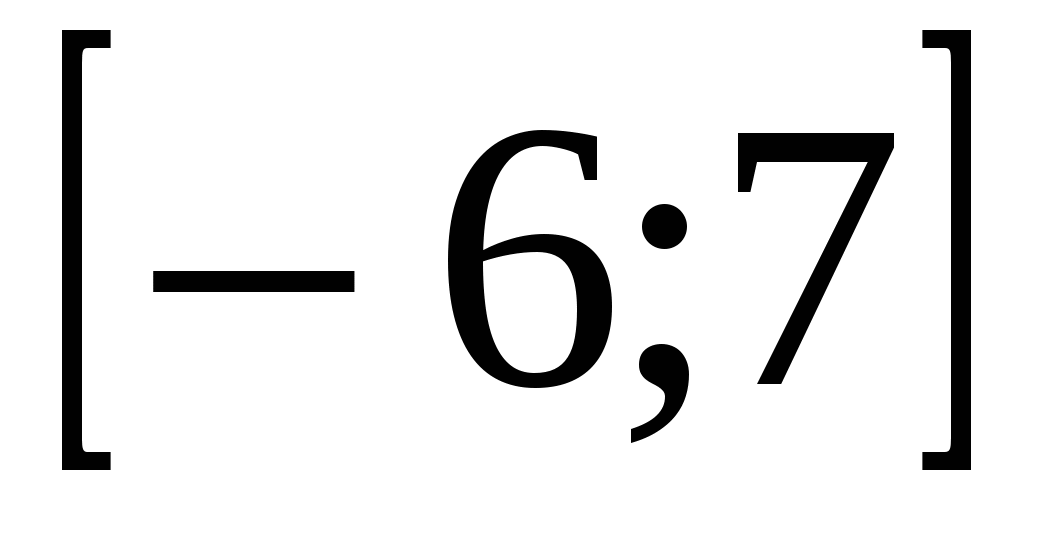 ? ?
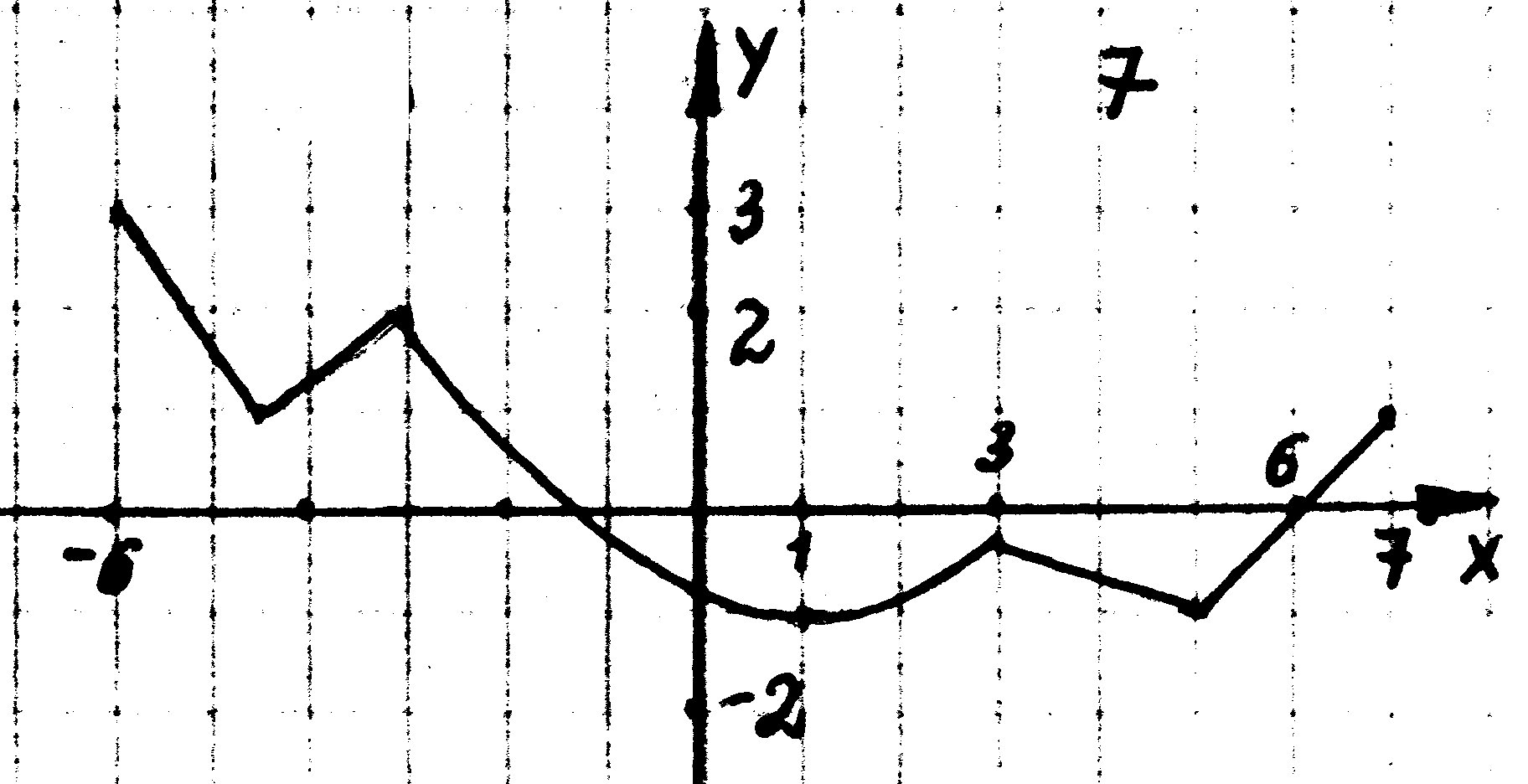
А5. Найдите область значений функции

А6. Найдите производную функции
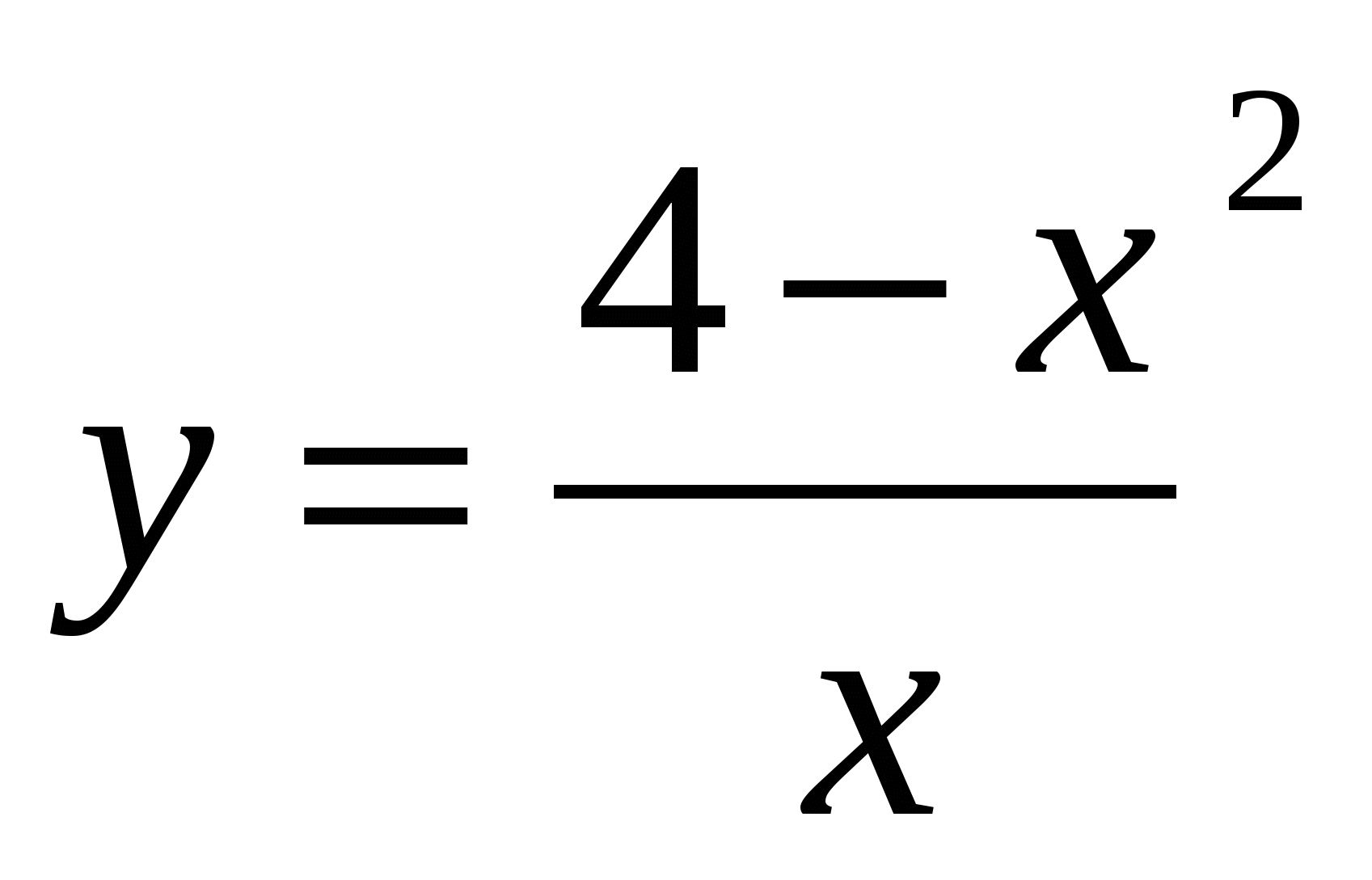
А7. Найдите производную функции
у=х 2– sinx в точке 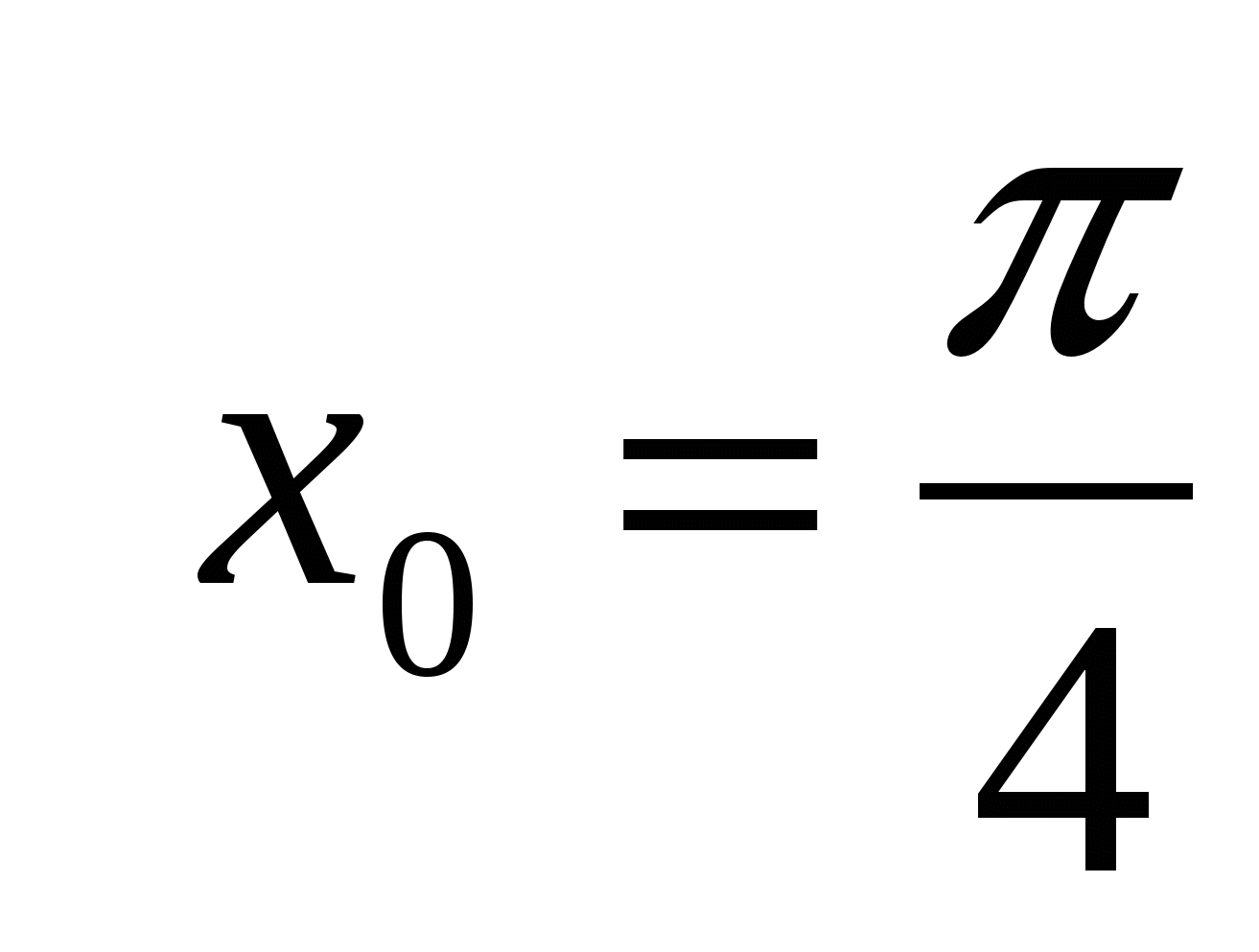
А8. Через точку графика функции 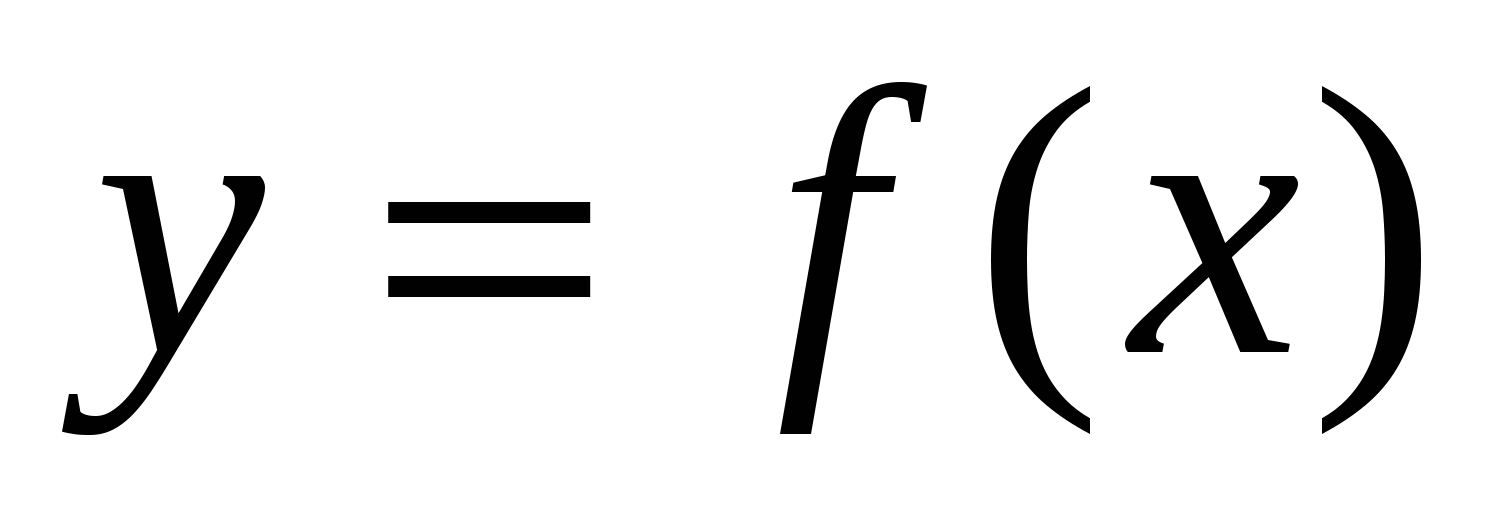 с абсциссой с абсциссой 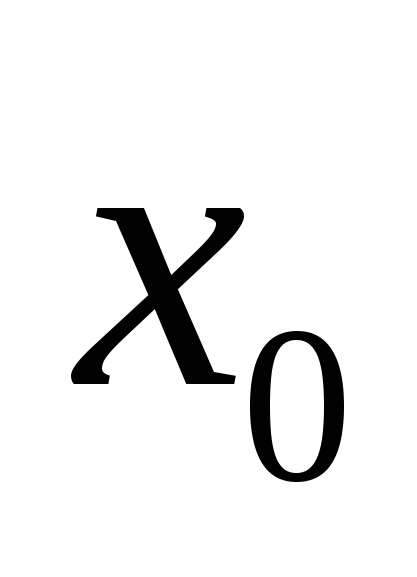 проведена касательная. Найдите тангенс угла наклона касательной к оси абсцисс, если проведена касательная. Найдите тангенс угла наклона касательной к оси абсцисс, если 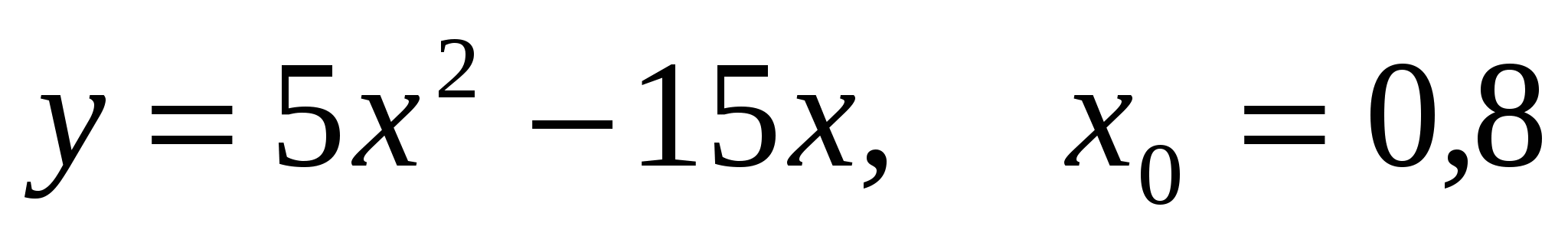
|
А9.Функция 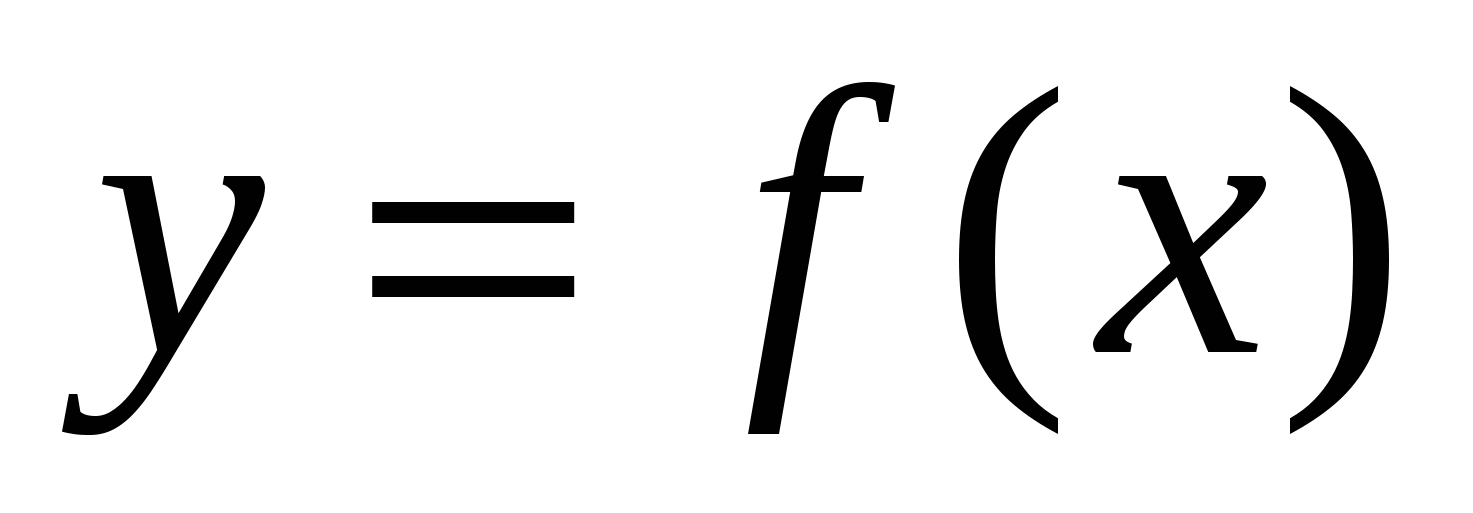 определена на промежутке определена на промежутке 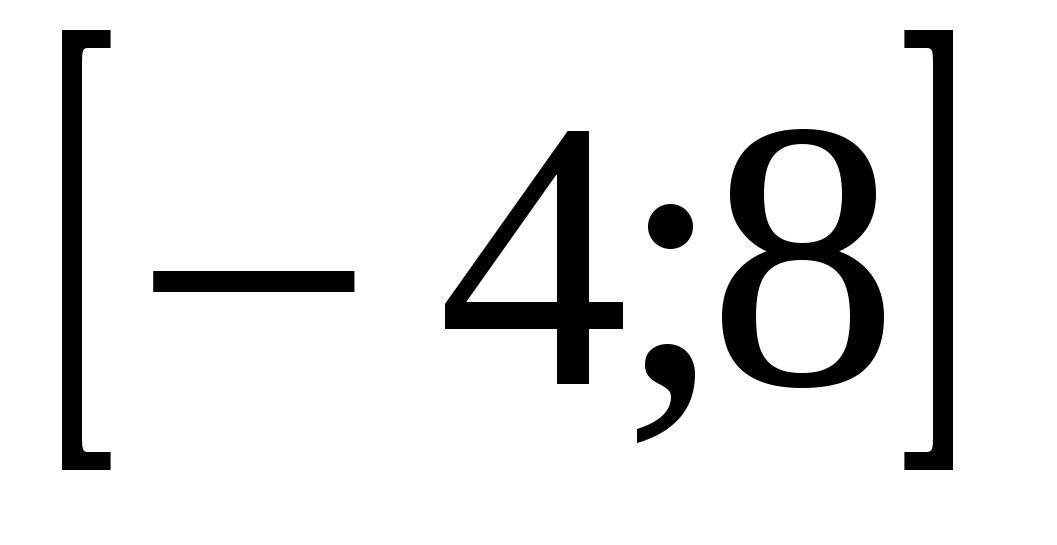 . .
График ее производной изображен на рисунке.
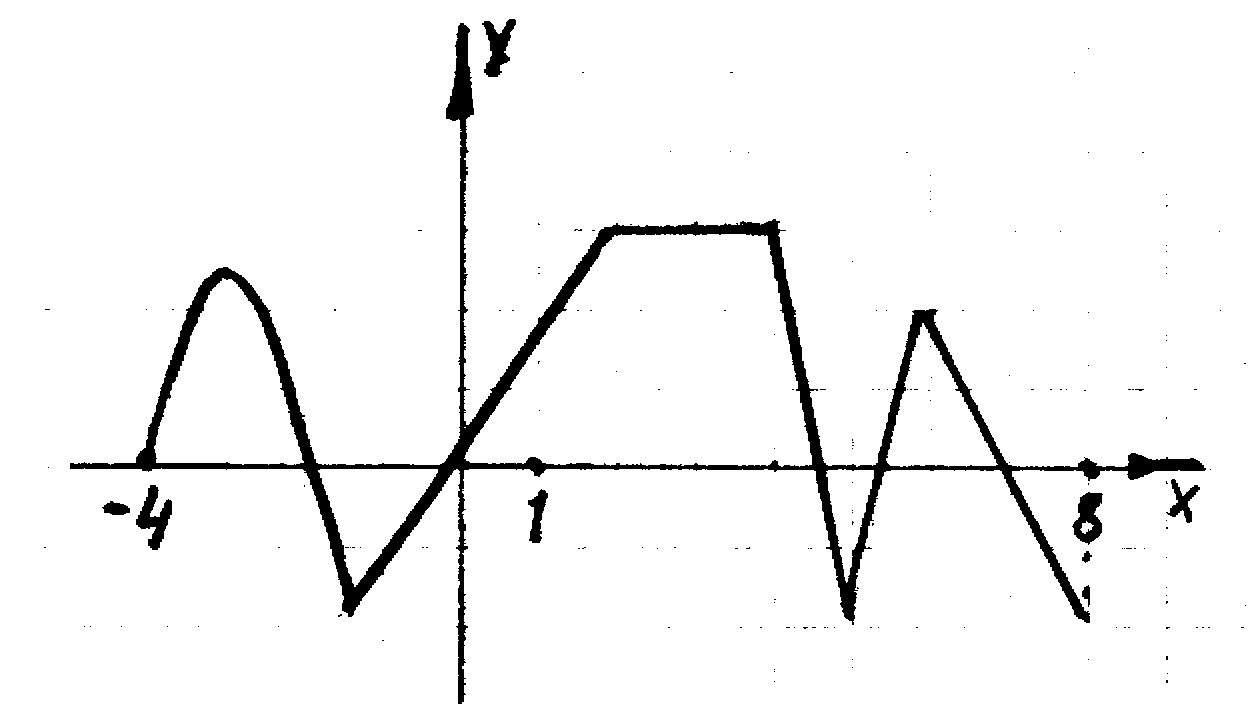
Укажите число промежутков возрастания функции.
А10.Точка движется по координатной прямой согласно закону 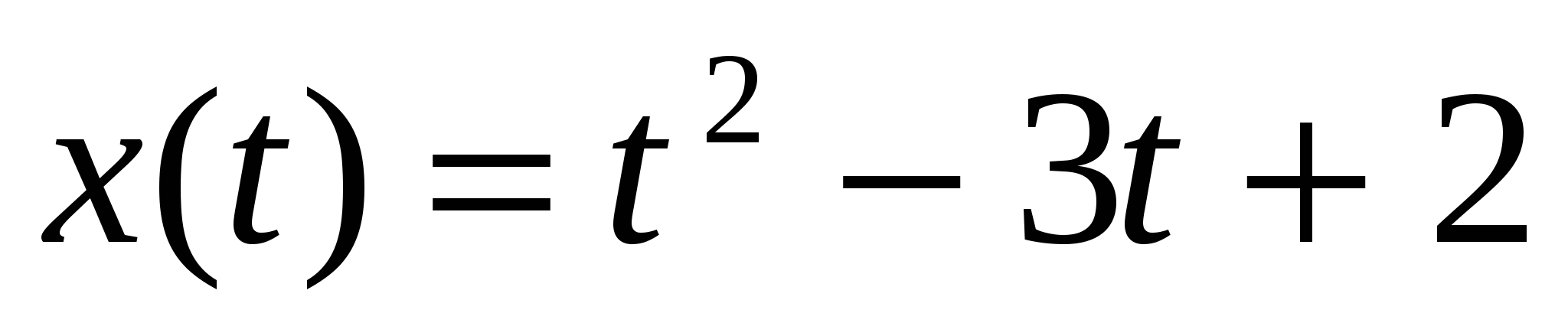 , где , где 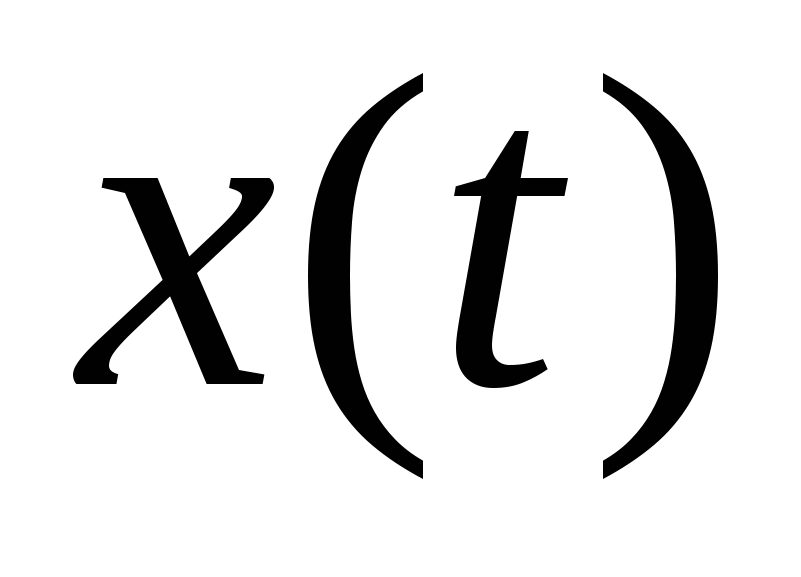 – координата точки в момент времени t. В какой момент времени скорость точки будет равна 7? – координата точки в момент времени t. В какой момент времени скорость точки будет равна 7?
В1.Найдите tgх, если cosx = –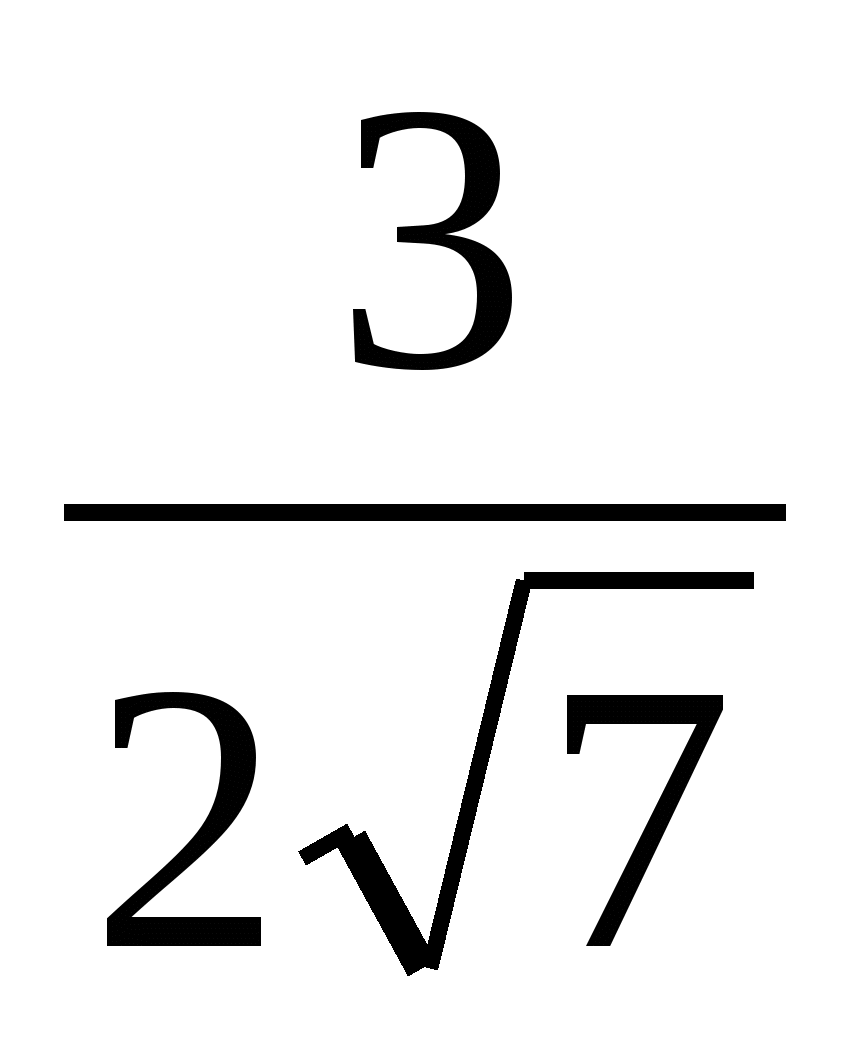 , ,
х  ( (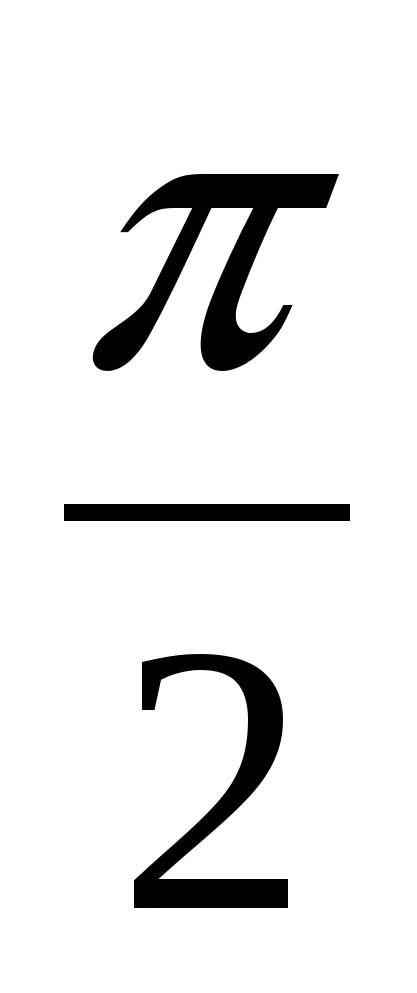 ; ; ). ).
В2. Найдите минимум функции 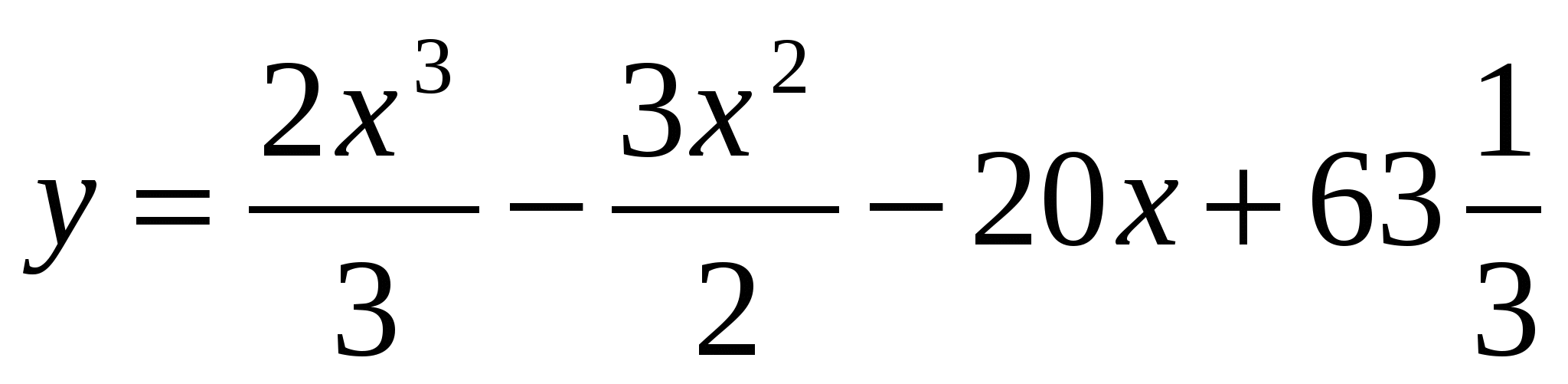
|
В3.Касательные к графику функции 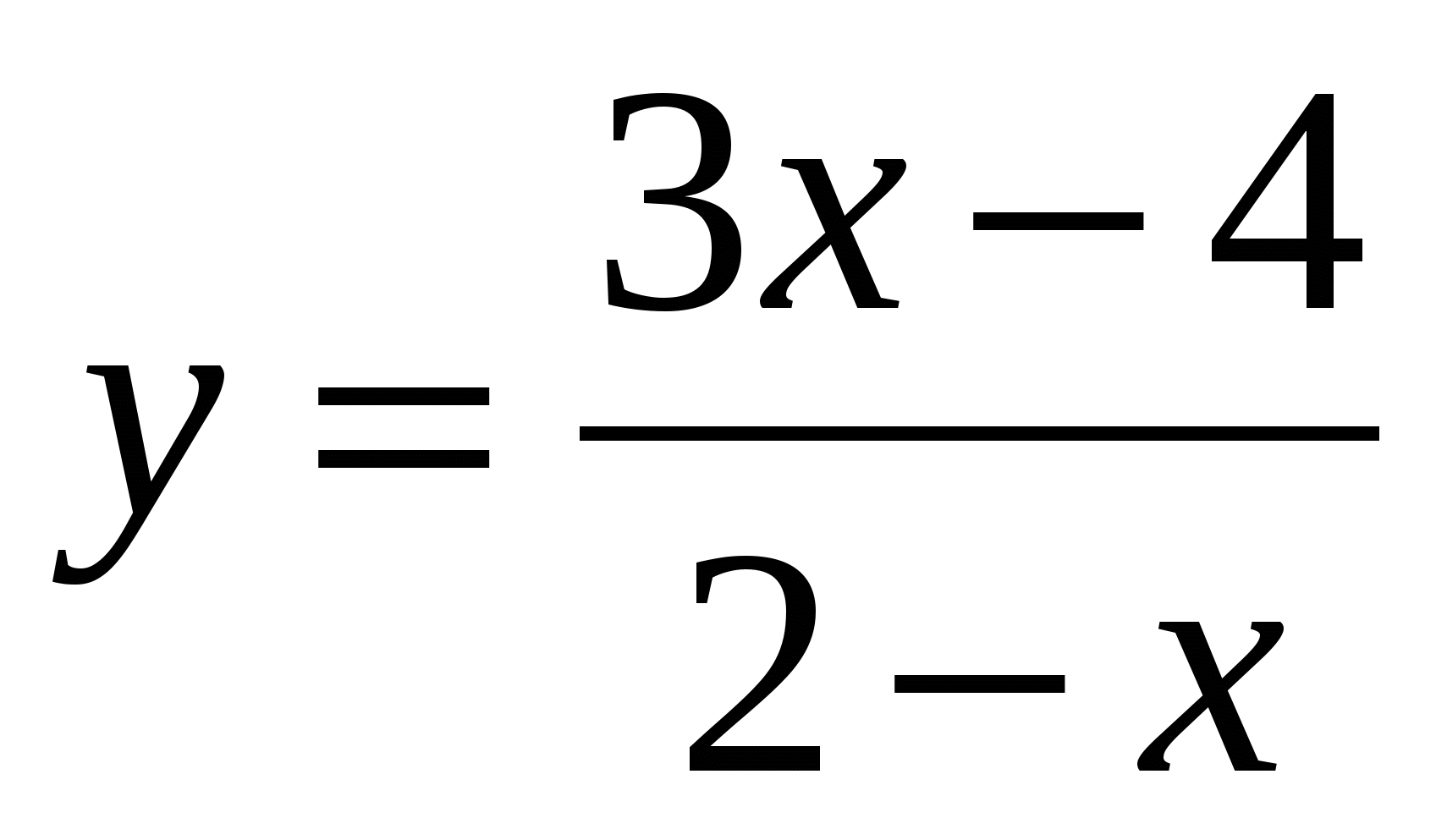 образуют с осью ОХ угол 450 в точках, сумму абсцисс которых нужно найти. образуют с осью ОХ угол 450 в точках, сумму абсцисс которых нужно найти.
В4. Найдите значение выражения 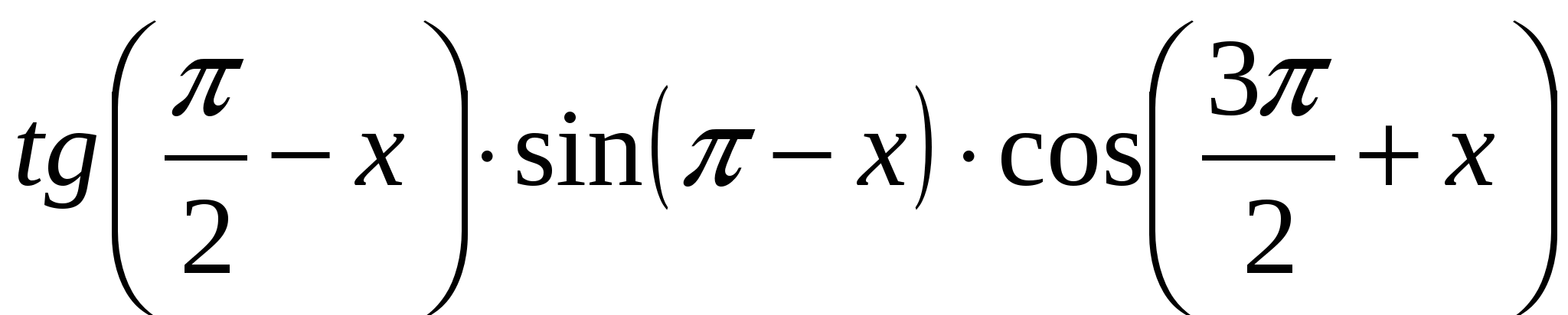 при при 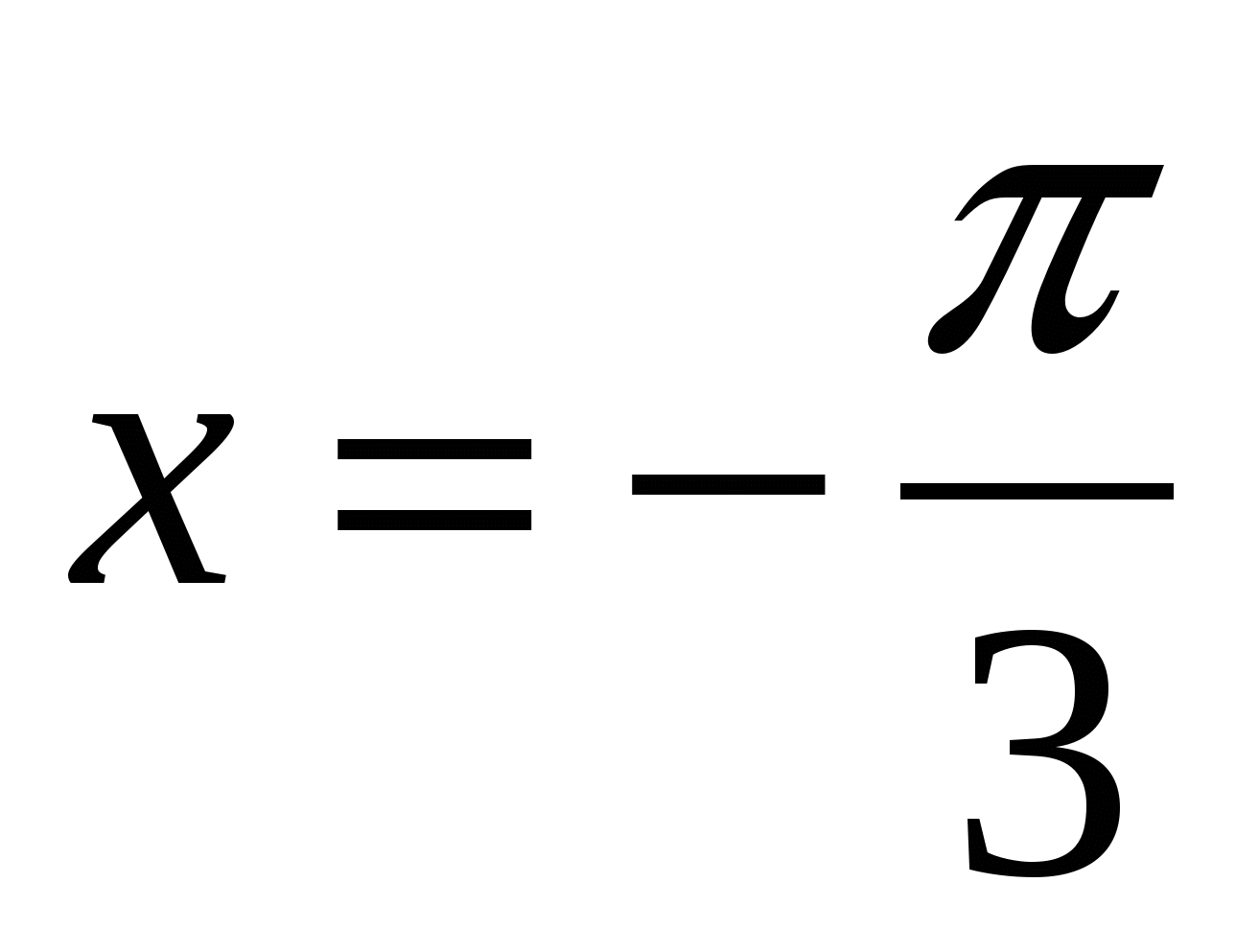 . .
В5. Найдите наибольшее значение функции
у = 2,5cosx на отрезке [– 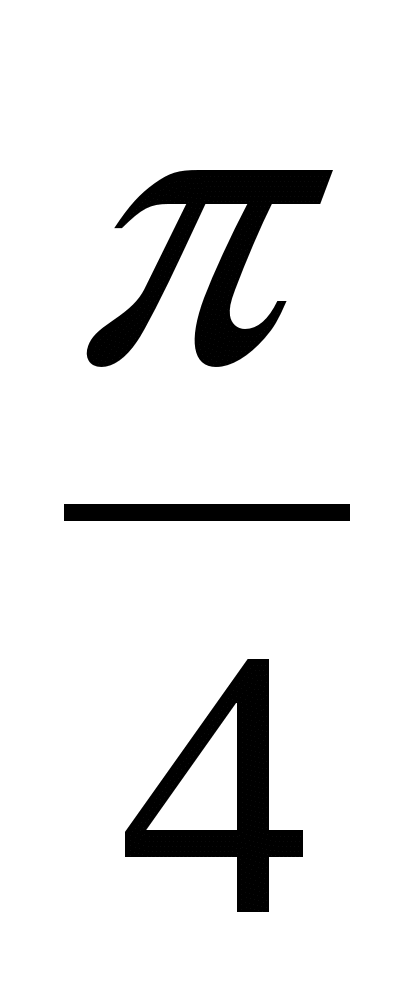 ; ; 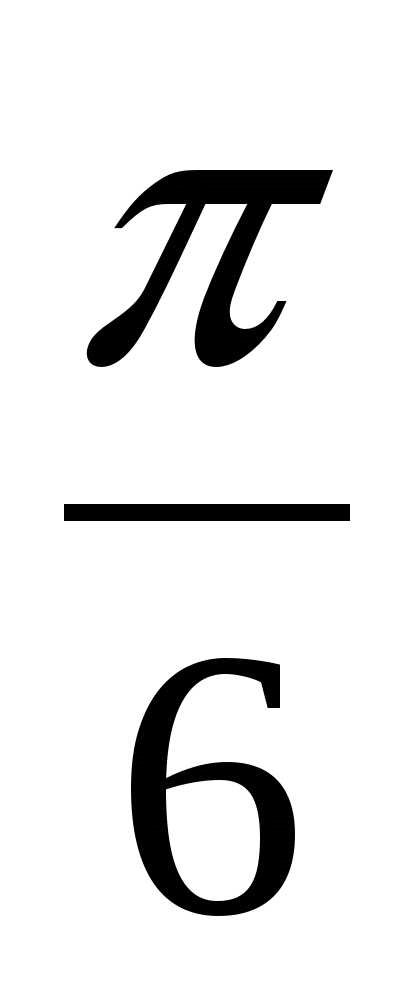 ]. ].
С1. Решите уравнение
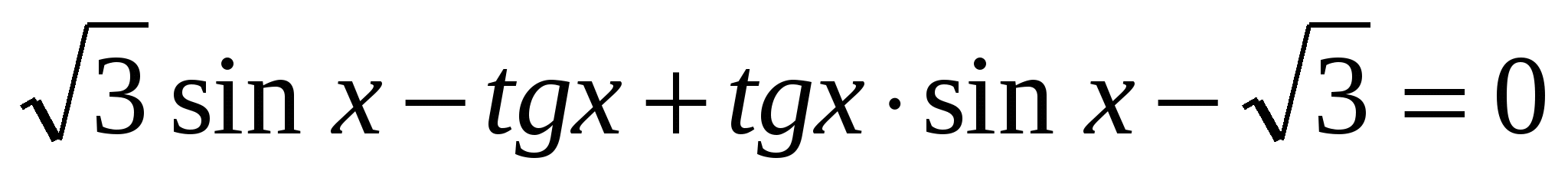 , найти корни, принадлежащие промежутку � , найти корни, принадлежащие промежутку �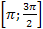 � �
С2. При каком значении к функция у= кх2+6х-1 имеет максимум в точке х=3?
С3. В треугольник с основанием 18 и высотой 12 вписан прямоугольник так, что одна его сторона принадлежит основанию треугольника. Чему равна наибольшая площадь такого прямоугольника?
|
 Скачать 16.15 Kb.
Скачать 16.15 Kb.