№
|
Изучаемый материал
|
Кол-во часов
|
Характеристика основных видов деятельности ученика (на уровне учебных действий)
|
Алгебра 9 класс (102 часа).
Рациональные неравенства и их системы
Цель:
- иметь представление о понятиях: линейное, квадратное, рациональное неравенство; область допустимых значений неравенств;
- овладеть умениями: определять область допустимых значений; решать линейные, квадратные, рациональные неравенства и неравенства с модуле; решать неравенства методом интервалов.
|
1-3
|
Линейные и квадратные неравенства
|
3
|
Распознавать линейные и квадратные неравенства, решать линейные неравенства и квадратные неравенства с одной переменной, дробно-рациональные неравенства, неравенства, содержащие модуль.
Понимать простейшие понятия теории множеств, приводить примеры конечных и бесконечных множеств, задавать множества, находить объединение и пересечение конкретных множеств.
Описывать множество целых чисел, множество рациональных чисел, множество действительных чисел, соотношение между этими множествами.
Решать системы линейных и квадратных неравенств, системы рациональных неравенств, двойные неравенства.
|
4-8
|
Рациональные неравенства
|
5
|
9-10
|
Множества и операции над ними
|
2
|
11-13
|
Системы рациональных неравенств
|
3
|
14
|
Обобщающий урок по теме: Рациональные неравенства и их системы
|
1
|
15
|
Контрольная работа № 1. Неравенства и системы неравенств.
|
1
|
16
|
Анализ контрольной работы.
|
1
|
Системы уравнений
Цель:
- иметь представление о системе рациональных уравнений, о составлении математической модели;
- овладеть умениями: выполнять равносильные преобразования, решая уравнения и системы уравнений с двумя переменными; решать уравнения и системы уравнений различными методами: графическим, подстановкой, алгебраического сложения, введения новых переменных; излагать информацию, интерпретируя факты, разъясняя значение и смысл теории.
|
17-20
|
Системы рациональных уравнений. Основные понятия
|
4
|
Иметь понятие о решении системы уравнений и неравенств, знают равносильные преобразования уравнений и неравенств с двумя переменными.
Уметь определять понятия, приводить доказательства.
Решать системы уравнений, простые нелинейные системы уравнений двух переменных различными методами.
Строить графики уравнений с двумя переменными;
применять графический метод, метод подстановки, метод алгебраического сложения и метод введения новой переменной при решении практических задач.
Решать неравенства и системы неравенств, используя графические представления.
Использовать функционально – графическое представление для решения и исследования уравнений и систем
составлять математические модели реальных ситуаций и работать с составленной моделью.
|
21-24
|
Методы решения систем уравнений
|
4
|
25-28
|
Системы уравнений как математические модели реальных ситуаций
|
4
|
29
|
Обобщающий урок. Системы рациональных уравнений.
|
1
|
30
|
Контрольная работа № 2. Системы рациональных уравнений
|
1
|
31
|
Анализ контрольной работы. Решение систем уравнений.
|
1
|
Числовые функции
Цель:
овладеть навыками нахождения области определения функции;
овладеть умениями: задания функции различными способами; построения графика функции по словесной модели;
иметь представление о таких фундаментальных понятиях математики, как функция, ее область определения, область значений, о различных способах задания функции: аналитическом, графическом, табличном, словесном;
овладеть умениями: применять понятия четности и нечетности, ограниченности, непрерывности, монотонности функций; строить и читать графики функций; находить наибольшее и наименьшее значения на заданном промежутке, решая практические задачи.
|
32-35
|
Определение числовой функции. Область определения, область значений функции
|
4
|
Находить значения функции, заданной формулой, таблицей, графиком, по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей.
Исследовать функцию на монотонность, определять наибольшее и наименьшее значение функции, ограниченность, выпуклость, четность, нечетность, область определения и множество значений; понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; распознавать виды изучаемых функций. Показывать схематически положение на координатной плоскости графиков функций вида у = С, у = kx + m, y= kx 2, y = k/x, y =  , y = |x|, y = ax 2 + bx + c в зависимости от значений коэффициентов, входящих в формулы. , y = |x|, y = ax 2 + bx + c в зависимости от значений коэффициентов, входящих в формулы.
Описывать свойства изученных функций, строить их графики.
Применять графические представления при решении уравнений, систем, неравенств.
|
36-38
|
Способы задания функций
|
3
|
39-42
|
Свойства функций
|
4
|
43-44
|
Четные и нечетные функции
|
2
|
45-46
|
Административная контрольная работа
|
2
|
47
|
Анализ административной контрольной работы.
|
1
|
48
|
Решение задач по теме: Числовые функции
|
1
|
49
|
Обобщающий урок по теме «Числовые функции. Свойства функции»
|
1
|
50
|
Контрольная работа № 3. Свойства функции
|
1
|
51-52
|
Анализ контрольной работы. Функция у = хn(n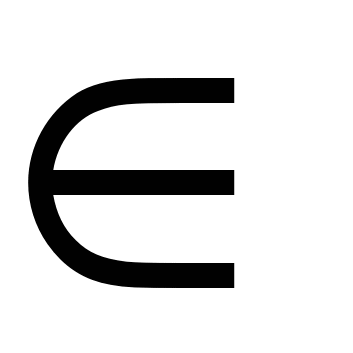 N), их свойства и графики N), их свойства и графики
|
2
|
53-54
|
Функция у = х-n(n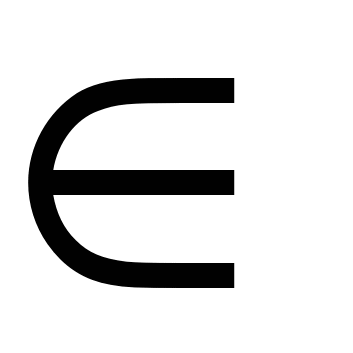 N), их свойства и графики N), их свойства и графики
|
2
|
55
|
Функция 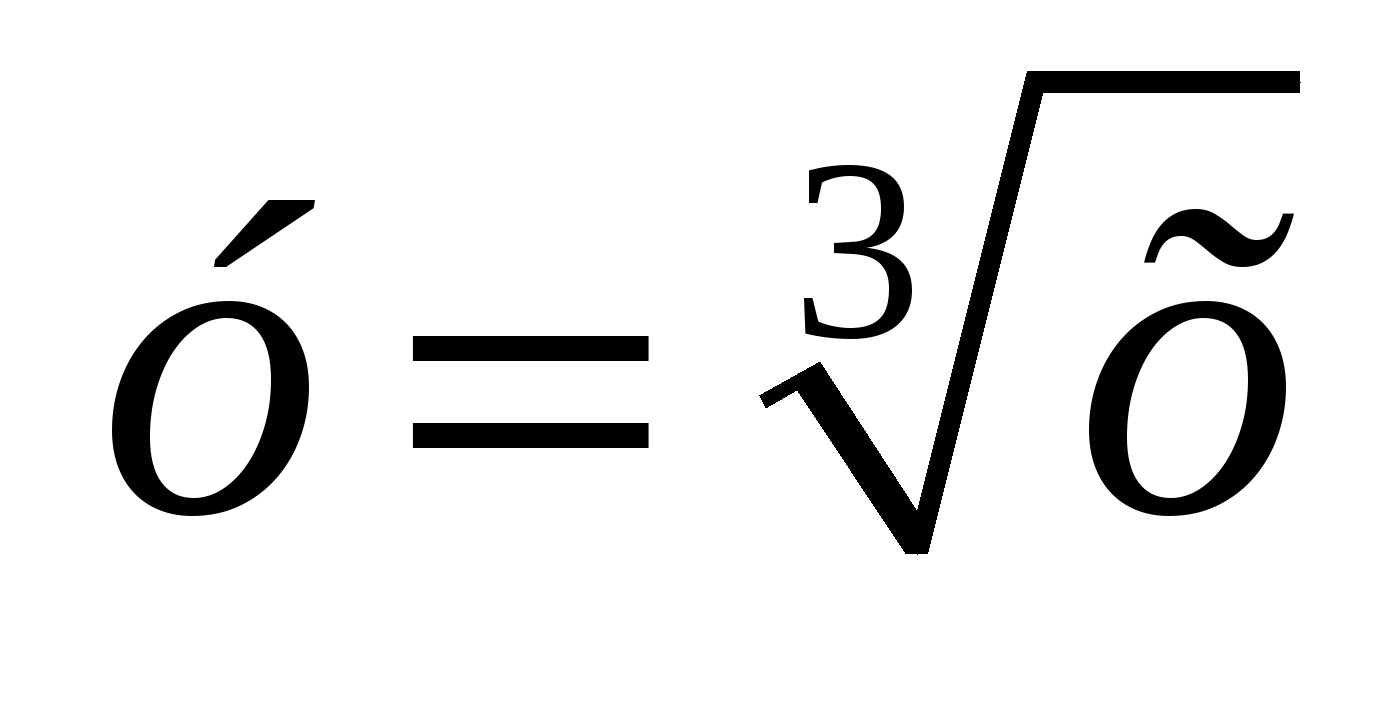 , ее свойства и график , ее свойства и график
|
1
|
56
|
Контрольная работа № 4. Числовые функции.
|
1
|
Прогрессии.
Цель:
- иметь представление о числовой последовательности, арифметической прогрессии и геометрической прогрессии, как частных случаях числовых последовательностей, о трех способах задания последовательности: аналитическом, словесном и рекуррентном;
- овладеть умениями: формулировать и обосновывать ряд свойств арифметической профессии, геометрической профессии, сводить их в одну таблицу;
- овладеть умениями: решать текстовые задачи, используя свойства арифметической прогрессии и геометрической прогрессии;
- овладеть умениями: выводить характеристическое свойство арифметической прогрессии и геометрической прогрессии применять их при решении математических задач.
|
57-61
|
Анализ контрольной работы. Числовые последовательности
|
5
|
Применять индексные обозначения, строить речевые высказывания с использованием терминологии, связанной с понятием последовательности.
Вычислять члены последовательностей, заданных формулой n-го члена или рекуррентной формулой. Устанавливать закономерность в построении последовательности, если известны первые несколько ее членов. Изображать члены последовательности точками на координатной плоскости.
Распознавать арифметическую и геометрическую прогрессии при разных способах задания. Выводить на основе доказательных рассуждений формулы общего члена арифметической и геометрической прогрессий, суммы первых п членов арифметической и геометрической прогрессий; решать задачи с использованием этих формул.
Рассматривать примеры из реальной жизни, иллюстрирующие изменение в арифметической прогрессии, в геометрической прогрессии; изображать соответствующие зависимости графически.
Решать задачи на сложные проценты, в том числе задачи из реальной практики (с использованием калькулятора)
Решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи.
|
62-65
|
Арифметическая прогрессия
|
4
|
66-69
|
Геометрическая прогрессия
|
4
|
70
|
Обобщающий урок по теме. Арифметическая и геометрическая прогрессии.
|
1
|
71
|
Контрольная работа № 5. Прогрессии.
|
1
|
72
|
Анализ контрольной работы
|
1
|
Элементы комбинаторики, статистики и теории вероятностей
Цель:
- иметь представление о комбинаторных задачах, элементах комбинаторики: перестановке, перемещении, сочетании; о понятии «среднее арифметическое», размахе ряда чисел, моде ряда чисел, о медиане произвольного ряда;
- иметь представление о новом математическом направлении – теории вероятностей, о понятии множества и операции над ними, о простейших вероятностных задачах;
|
73-75
|
Комбинаторные задачи
|
3
|
Проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений.
Использовать примеры для иллюстрации и контр примеры для опровержения утверждений.
Извлекать информацию, представленную в таблицах, на диаграммах графиках, составлять таблицы, строить диаграммы и графики.
Решать комбинаторные задачи путем систематического перебора возможных вариантов, а также с использованием правила умножения.
Находить размах, моду, среднее значение;
находить частоту события, используя собственные наблюдения и готовые статистические данные.
Приводить примеры достоверных и невозможных событий
находить вероятности случайных событий в простейших случаях
|
76-77
|
Статистика – дизайн информации
|
2
|
78-80
|
Простейшие вероятностные задачи
|
3
|
81-82
|
Экспериментальные данные и вероятности событий
|
2
|
83
|
Обобщающий урок по теме. Элементы комбинаторики, статистики и теории вероятностей.
|
1
|
84
|
Контрольная работа № 6. Элементы комбинаторики, статистики и теории вероятностей.
|
1
|
85-89
|
Множества. Элементы логики
|
5
|
Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение множеств. Приводить примеры несложных классификаций.
Использовать теоретико-множественную символику и язык при решении задач в ходе изучения различных разделов курса.
Иллюстрировать математические понятия и утверждения примерами. Использовать примеры и контр примеры в аргументации.
Конструировать математические предложения с помощью связок если…, то…, в том и только том случае, логических связок и, или
|
90-102
|
Итоговое повторение Итоговая контрольная работа
|
13
|
|
|
|
102
|
|
 Скачать 2.09 Mb.
Скачать 2.09 Mb.