|
|
№ п/п
|
Тема
|
Кол-во
часов
|
Характеристика основных видов деятельности ученика (на уровне учебных действий).
|
|
Геометрия 7 класс (68 часов).
Начальные геометрические сведения.
Цель: систематизировать знаний учащихся об основных свойствах простейших геометрических фигур, ввести понятие равенства фигур.
|
|
1
|
Прямая и отрехок. Луч и угол.
Сравнение отрезков и углов.
Измерение отрезков. Измерение углов.
Перпендикулярные прямые.
Решение задач.
Контрольная работа №1.
|
11
|
Формулировать определения и иллюстрировать понятия отрезка, луча; угла, прямого, острого, тупого и развернутого углов; вертикальных и смежных углов; биссектрисы угла.
Формулировать определения перпендикулярных прямых; перпендикуляра и наклонной к прямой; серединного перпендикуляра к отрезку; распознавать и изображать их на чертежах и рисунках.
|
|
Треугольники.
Цель: сформировать умение доказывать равенство треугольников, опираясь на изученные признаки; отработать навыки решения простейших задач на построение с помощью циркуля и линейки.
|
|
2
|
Первый признак равенства треугольников.
Медианы, биссектрисы и высоты треугольника.
Второй и третий признаки равенства треугольников.
Задачи на построение.
Решение задач.
Контрольная работа №2.
|
18
|
Формулировать определения прямоугольного, остроугольного, тупоугольного, равнобедренного, равностороннего треугольников; высоты, медианы, биссектрисы; распознавать и изображать их на чертежах и рисунках.
Формулировать определение равных треугольников. Формулировать и доказывать теоремы о признаках равенства треугольников.
Решать задачи на построение с помощью циркуля и линейки.
Находить условия существования решения, выполнять построение точек, необходимых для построения искомой фигуры. Доказывать, что построенная фигура удовлетворяет условиям задачи (определять число решений задачи при каждом возможном выборе данных)
Решать задачи на построение, доказательство и вычисления.
Выделять в условии задачи условие и заключение. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Опираясь на данные условия задачи, проводить необходимые рассуждения. Интерпретировать полученный результат и сопоставлять его с условием задачи
|
|
Параллельные прямые
Цель: дать систематические сведения о параллельных прямых; ввести аксиому параллельных прямых.
|
|
3
|
Признаки параллельности двух прямых.
Аксиома параллельных прямых.
Решение задач.
Контрольная работа №3.
|
12
|
Формулировать определения параллельных прямых; углов, образованных при пересечении двух параллельных прямых секущей; распознавать и изображать их на чертежах и рисунках.
|
|
Соотношения между сторонами и углами треугольника
Цель: расширить знаний учащихся о треугольниках.
|
|
4
|
Сумма углов треугольника.
Соотношения между сторонами и углами треугольника.
Контрольная работа №4.
Прямоугольные треугольники.
Построение треугольника по трём элементам.
Решение задач.
Контрольная работа №5.
|
18
|
Объяснять и иллюстрировать неравенство треугольника.
Формулировать и доказывать теоремы о свойствах и признаках равнобедренного треугольника, соотношениях между сторонами и углами треугольника, сумме углов треугольника, внешнем угле треугольника,
Исследовать свойства треугольника с помощью компьютерных программ.
Решать задачи на построение, доказательство и вычисления. Выделять в условии задачи условие и заключение. Моделировать условие задачи с помощью чертежа или рисунка, проводить дополнительные построения в ходе решения. Опираясь на данные условия задачи, проводить необходимые рассуждения. Интерпретировать полученный результат и сопоставлять его с условием задачи.
|
|
5
|
Повторение. Решение задач.
|
9
|
Знать материал, изученный в курсе математики за 7 класс.
Владеть общим приемом решения задач.
Уметь применять полученные знания на практике.
Уметь логически мыслить, отстаивать свою точку зрения и выслушивать мнение других, работать в команде.
|
|
|
Итого:
|
68
|
|
№
|
Изучаемый материал
|
Кол-во часов
|
Характеристика основных видов деятельности ученика (на уровне учебных действий)
|
Алгебра 8 класс (102 часа).
Алгебраические дроби
Цель:
иметь представление о понятиях: алгебраическая дробь, область допустимых значений, основное свойство алгебраической дроби, рациональное выражение;
овладеть умениями: сокращать дроби; приводить алгебраические дроби к общему знаменателю; складывать и вычитать алгебраические дроби с одинаковыми знаменателями.
|
1
|
Основные понятия
|
1
|
Иметь представление о числителе, знаменателе алгебраической дроби, о значении алгебраической дроби и о значении переменной, при которой алгебраическая дробь не имеет смысла.
Уметь находить рациональным способом значение алгебраической дроби, обосновывать свое решение, устанавливать, при каких значениях переменной алгебраическая дробь не имеет смысла, аргументировано отвечать на поставленные вопросы, осмысливать и устранять ошибки. Формулировать основное свойство алгебраической дроби и применять его для преобразования дробей.
Выполнять действия с алгебраическими дробями. Представлять целое выражение в виде многочлена, дробное — в виде отношения многочленов; доказывать тождества.
Формулировать определение степени с целым показателем. Формулировать, записывать в символической форме и иллюстрировать примерами свойства степени с целым показателем; применять свойства степени для преобразования выражений и вычислений.
|
2-3
|
Основное свойство алгебраической дроби.
|
2
|
4-5
|
Сложение и вычитание алгебраических дробей с одинаковыми знаменателями
|
2
|
6-9
|
Сложение и вычитание алгебраических дробей с разными знаменателями
|
4
|
10
|
Контрольная работа № 1
|
1
|
11-12
|
Умножение и деление алгебраических дробей. Возведение алгебраических дробей в степень
|
2
|
13-15
|
Преобразование рациональных выражений
|
3
|
16-17
|
Первые представления о решении рациональных уравнений
|
2
|
18-20
|
Степень с отрицательным целым показателем
|
3
|
21
|
Контрольная работа № 2
|
1
|
Функция 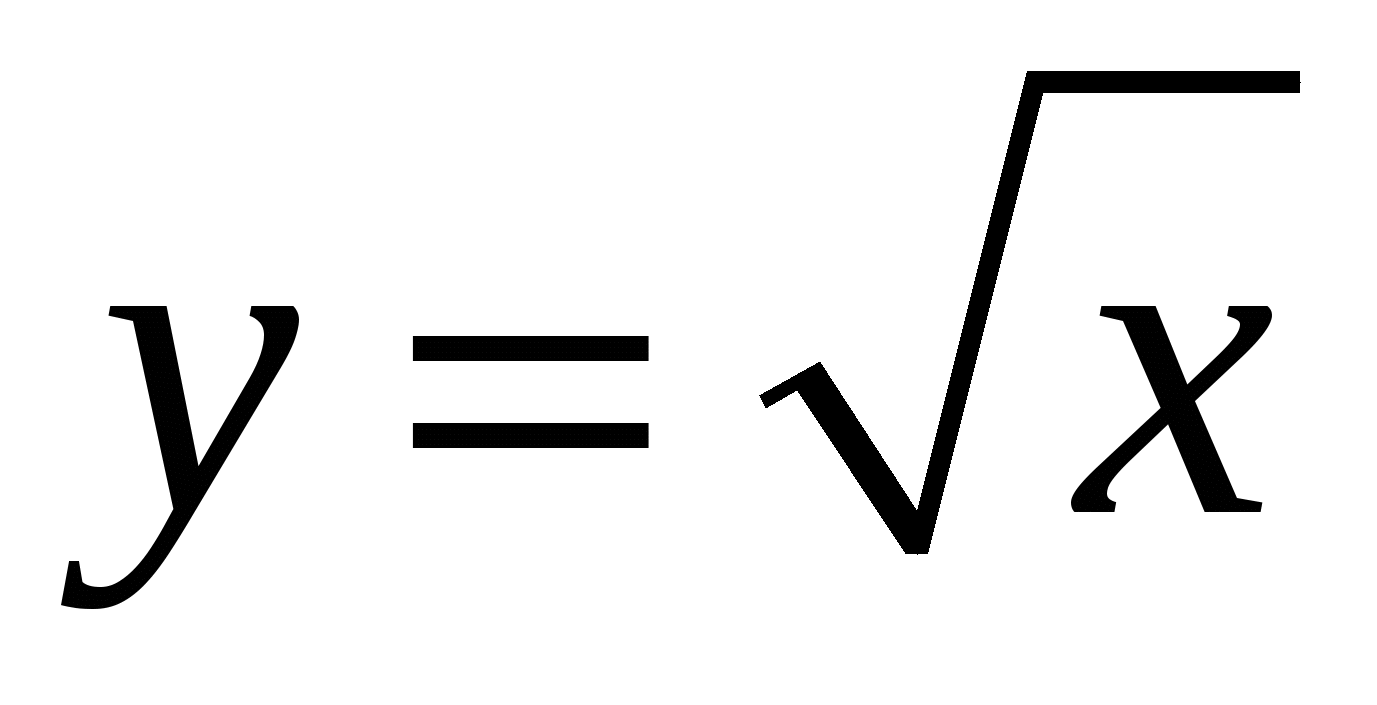 . Свойства квадратного корня
Цель:
иметь представление о квадратном корне, квадратном корне из неотрицательного числа, о подкоренном выражении, об иррациональных числах, о кубическом корне из неотрицательного числа, о корне n-й степени из неотрицательного числа;
овладеть умениями: извлекать квадратный корень и корень n-й степени из неотрицательного числа; строить и читать график функции у = √х; использовать алгоритм извлечения квадратного корня
|
22-23
|
Рациональные числа
|
2
|
Приводить примеры иррациональных чисел; распознавать рациональные и иррациональные числа; изображать числа точками координатной прямой.
Находить десятичные приближения рациональных и иррациональных чисел.
Сравнивать и упорядочивать действительные числа.
Описывать множество действительных чисел.
Использовать в письменной математической речи обозначения и графические изображения числовых множеств, теоретико-множественную символику.
Формулировать определение квадратного корня из числа.
Использовать графики функции у = х2 и 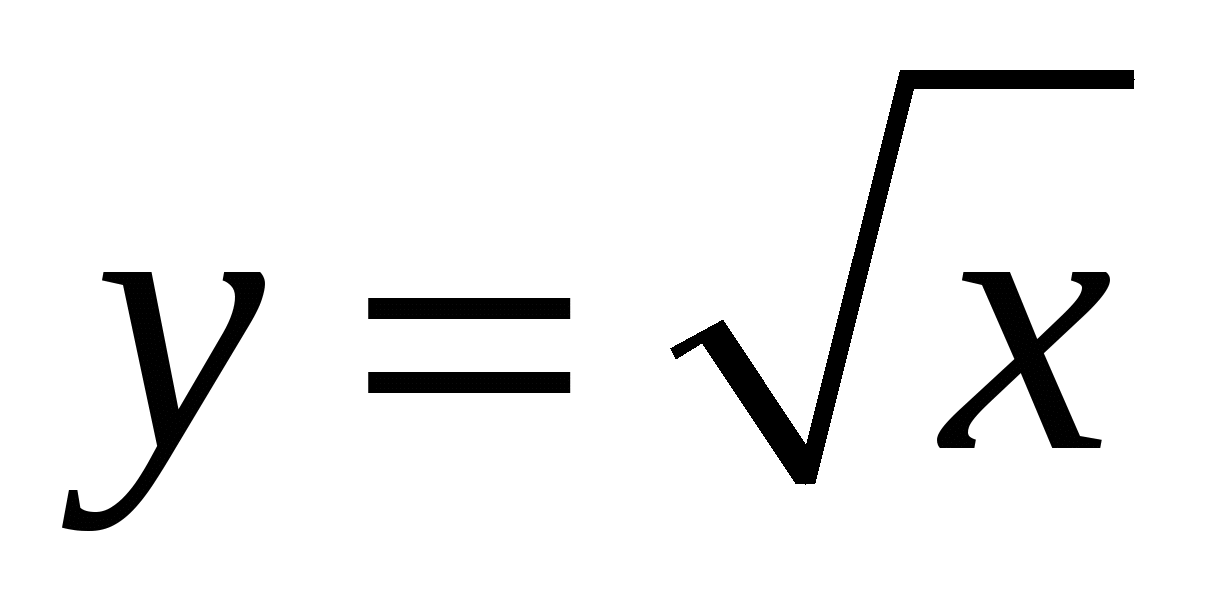 для нахождения квадратных корней. Вычислять точные и приближенные значения корней, используя при необходимости калькулятор; проводить оценку квадратных корней.
Доказывать свойства арифметических квадратных корней; применять их для преобразования выражений.
Вычислять значения выражений, содержащих квадратные корни; выражать переменные из геометрических и физических формул.
Исследовать уравнение вида 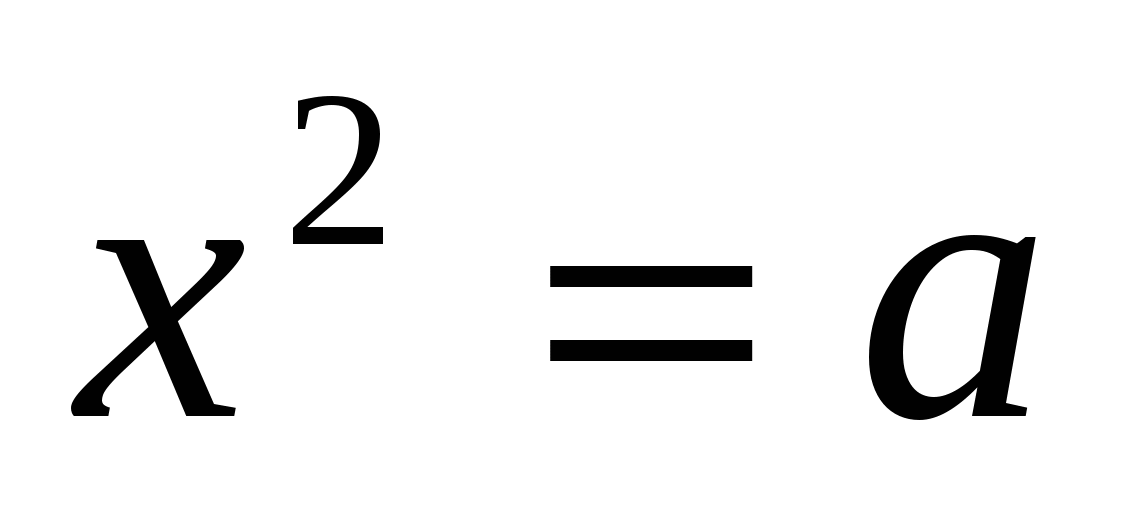 ; находить точные и приближенные корни при а > 0
|
24-25
|
Понятие квадратного корня из неотрицательного числа
|
2
|
26
|
Иррациональные числа
|
1
|
27
|
Множество действительных чисел
|
1
|
28-29
|
Функция 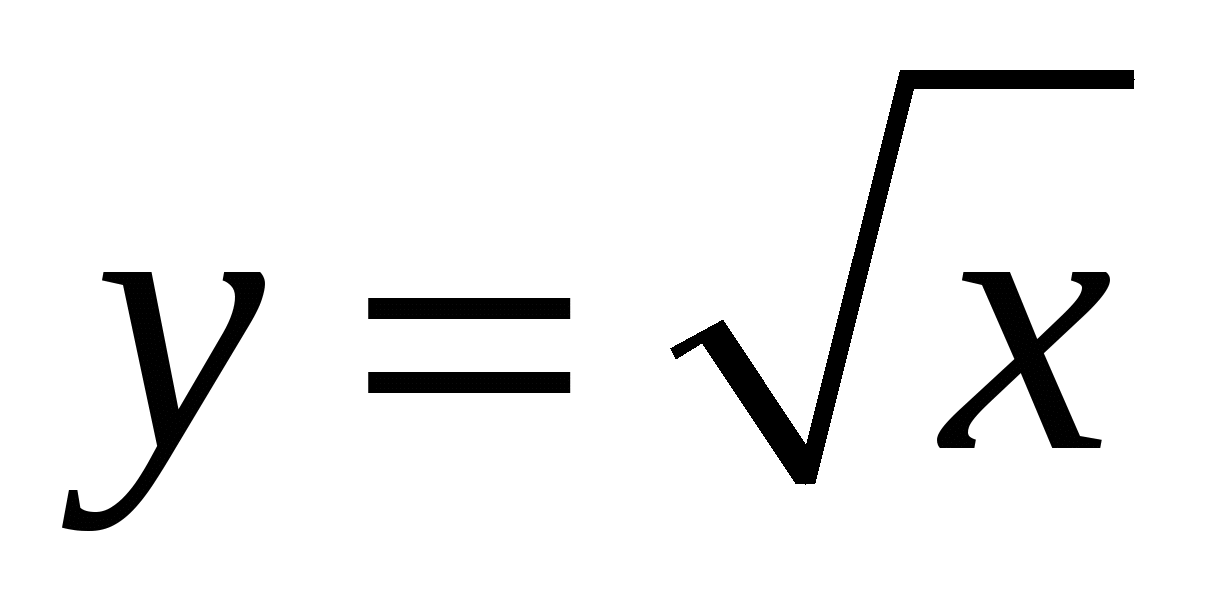, ее свойства и график.
|
2
|
30-31
|
Свойства квадратных корней
|
2
|
32-35
|
Преобразование выражений, содержащих операцию извлечения квадратного корня
|
4
|
36
|
Контрольная работа № 3
|
1
|
37-39
|
Модуль действительного числа
|
3
|
Квадратичная функция. Функция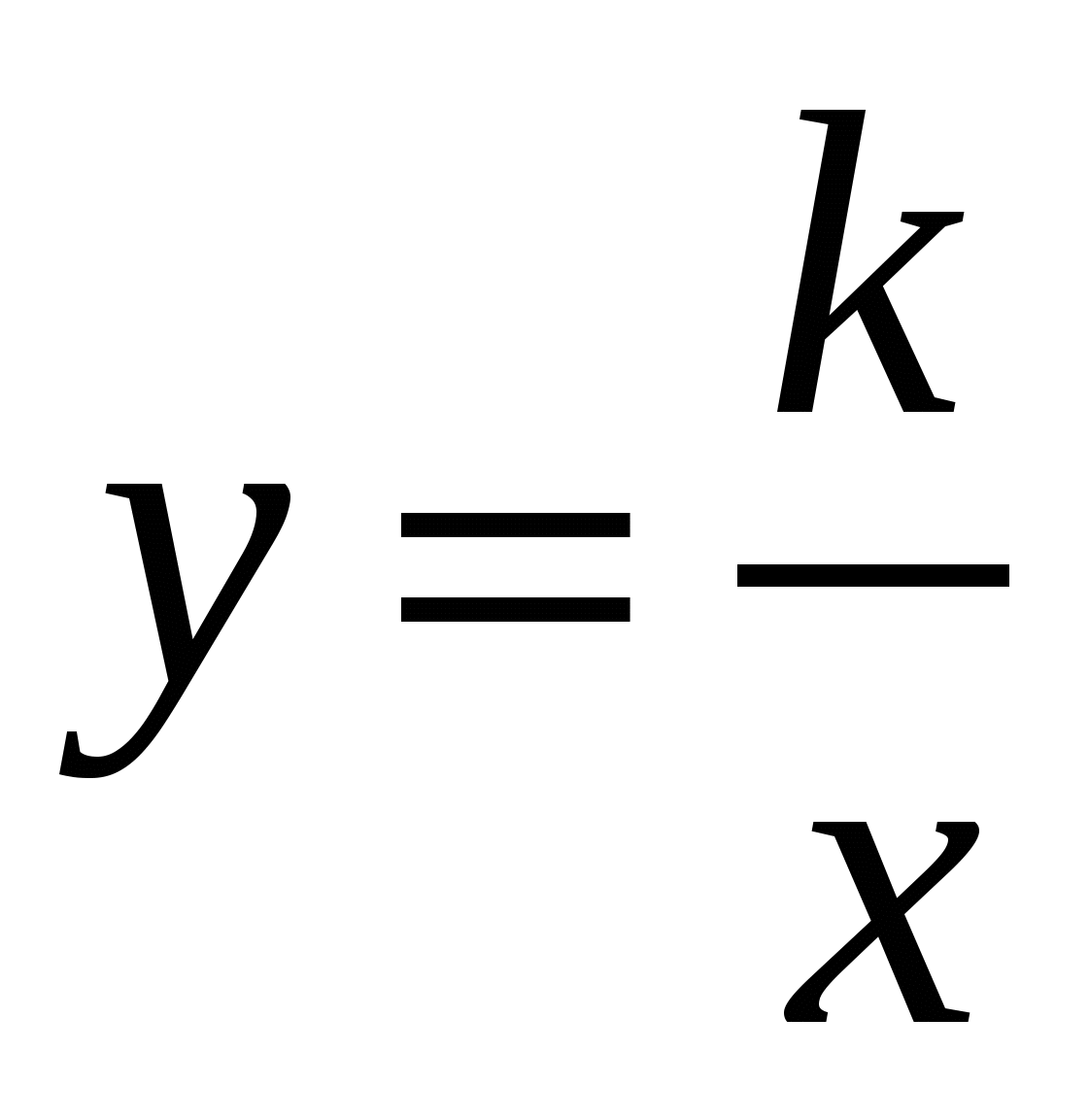 
Цель:
изучить функции у = кх2, у =k/x , их свойства и графики;
иметь представление о кусочно-заданных функциях, контрольных точках графика, параболе, оси симметрии параболы, асимптотах, оси симметрии гиперболы, об обратной пропорциональности, области значений функции, окрестности точки, о точках максимума и минимума;
овладеть умениями: построения графиков функций у = кх2, у = k/x и описания их свойств; использования алгоритма построения графиков функций у = f(x + l) + m, у = f(x + l), y = f(x)±m путем преобразования функции 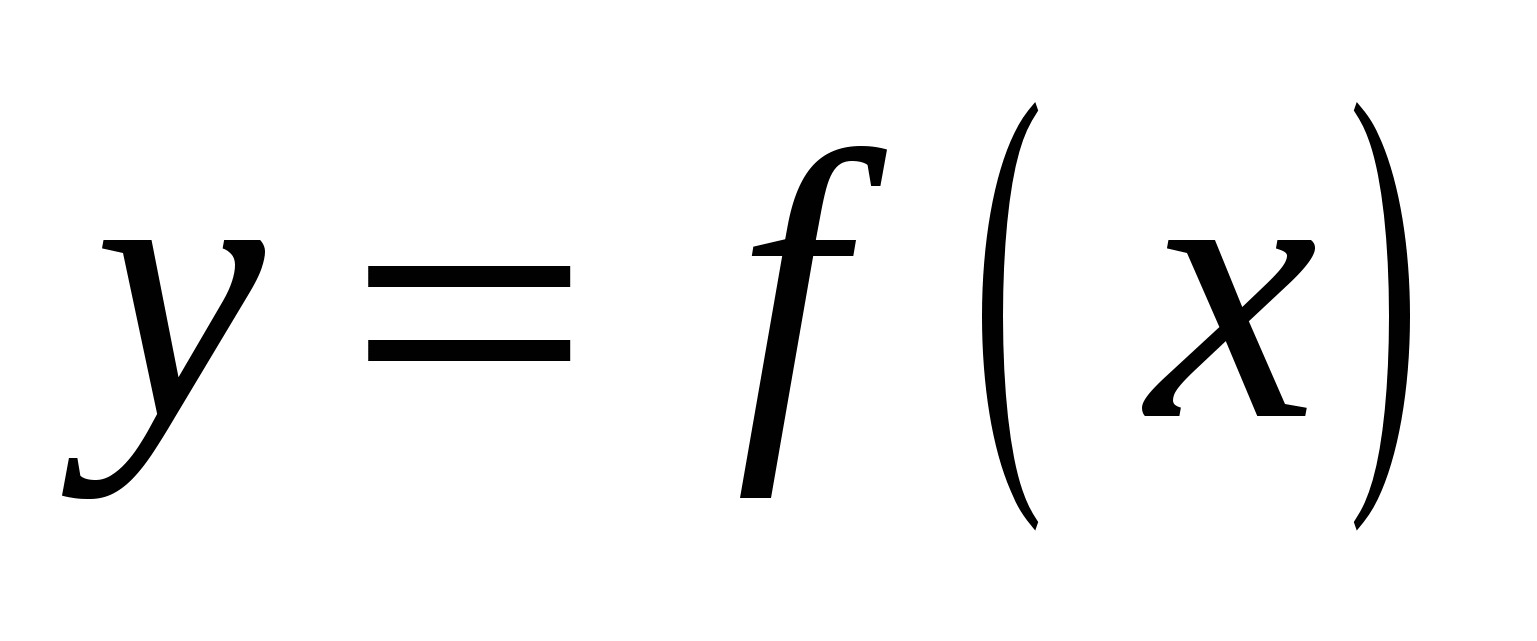 параллельным переносом вправо (влево)
|
40-42
|
Функция 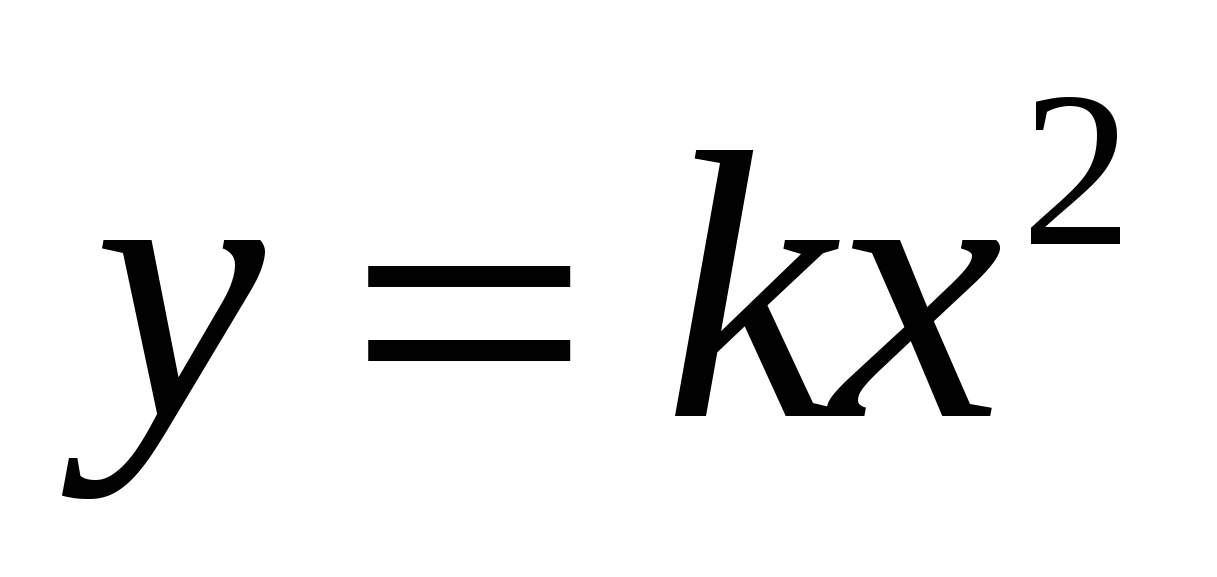 , ее свойства и график.
|
3
|
Знать, как строить график функции у = кх2, свойства функции.
Уметь упрощать функциональные выражения, строить графики кусочно-заданных функций, осуществлять проверку выводов, положений, закономерностей, теорем, работать с чертежными инструментами.
|
43-44
|
Функция 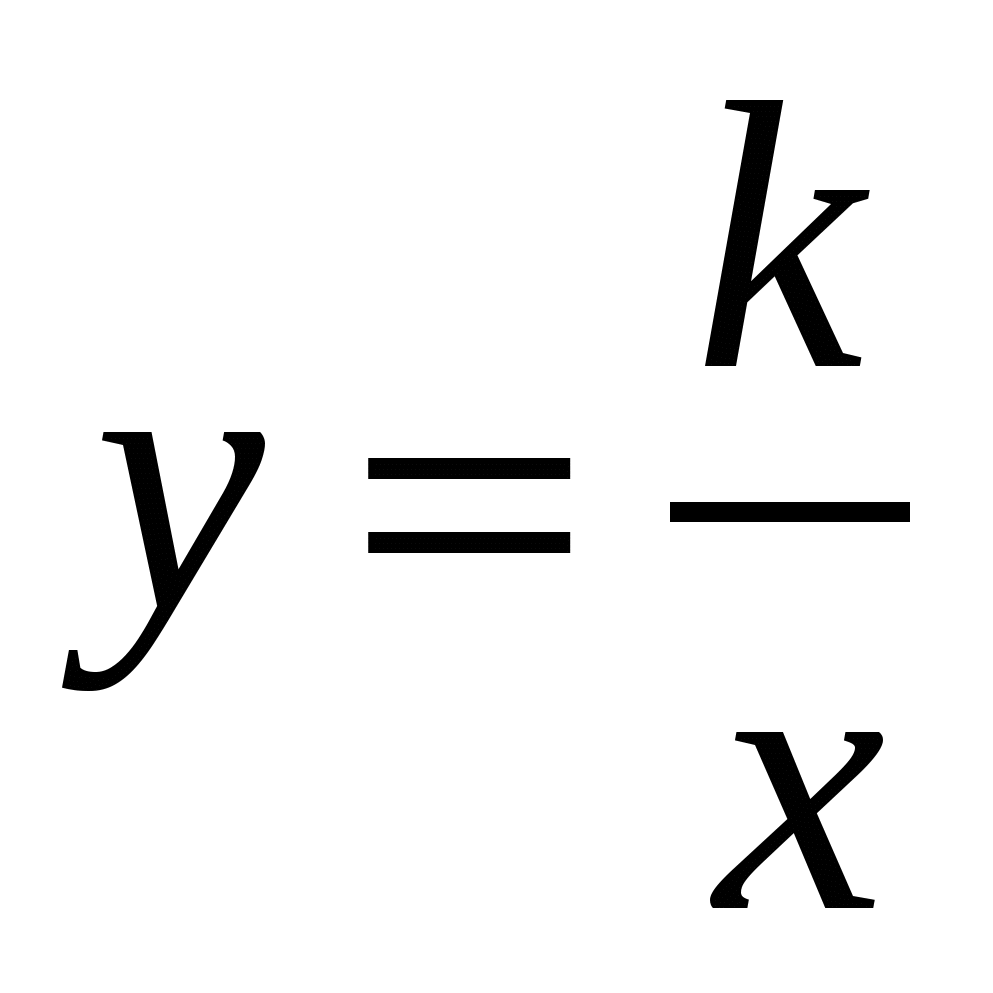 , ее свойства и график.
|
2
|
Иметь представление о функции вида у = k/x, о ее графике и свойствах.
Уметь графически решать уравнения и системы уравнений, определять число решений системы уравнений с помощью графического метода, решать нетиповые задачи, выполняя продуктивные действия эвристического типа.
|
45
|
Контрольная работа № 4
|
1
|
46-47
|
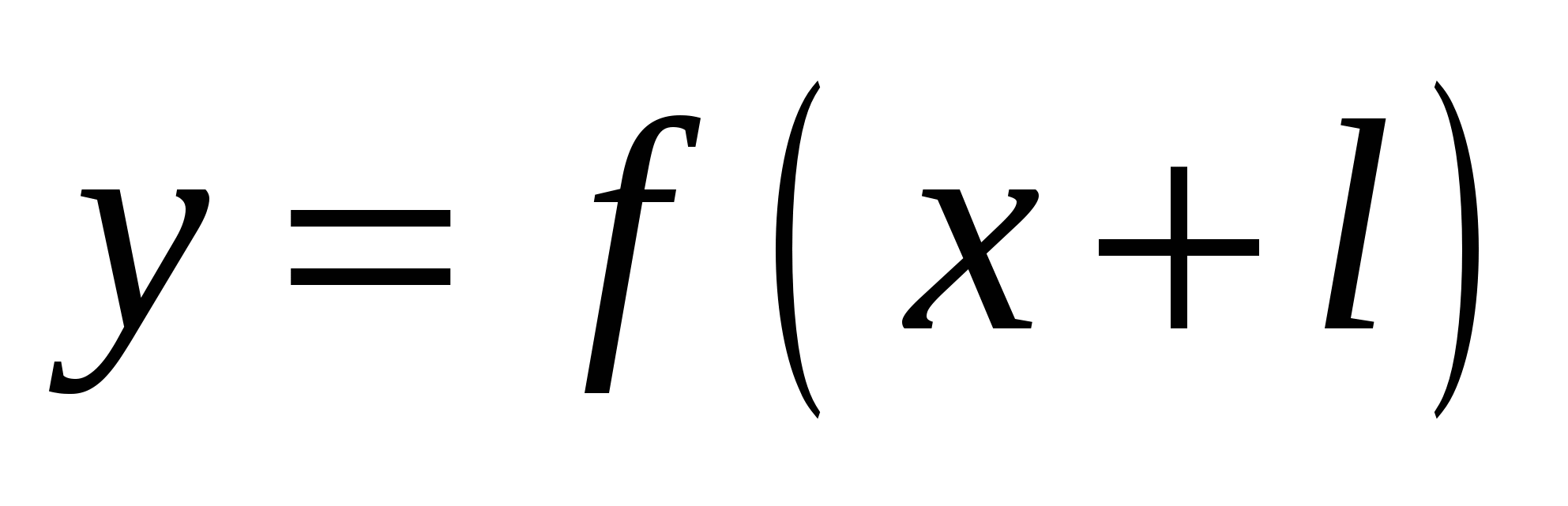Как построить график функции  , если известен график функции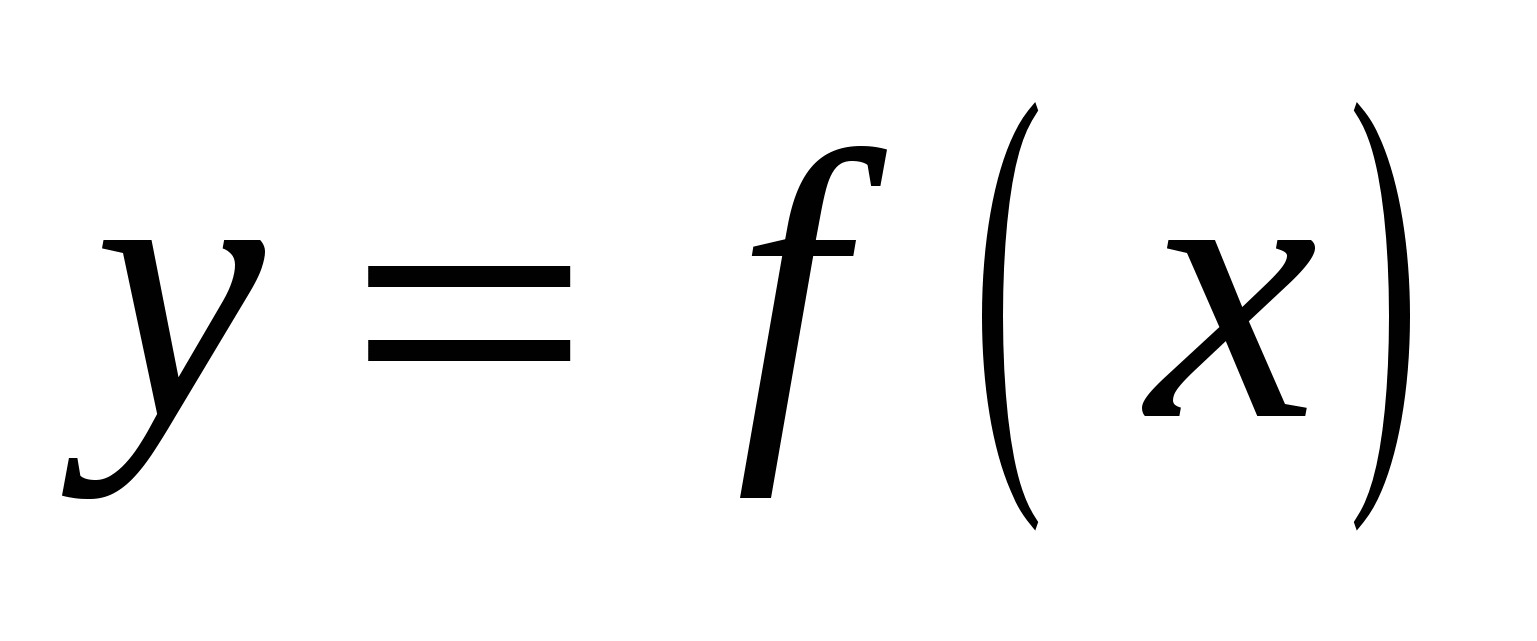
|
2
|
Иметь представление, как с помощью параллельного переноса вправо или влево построи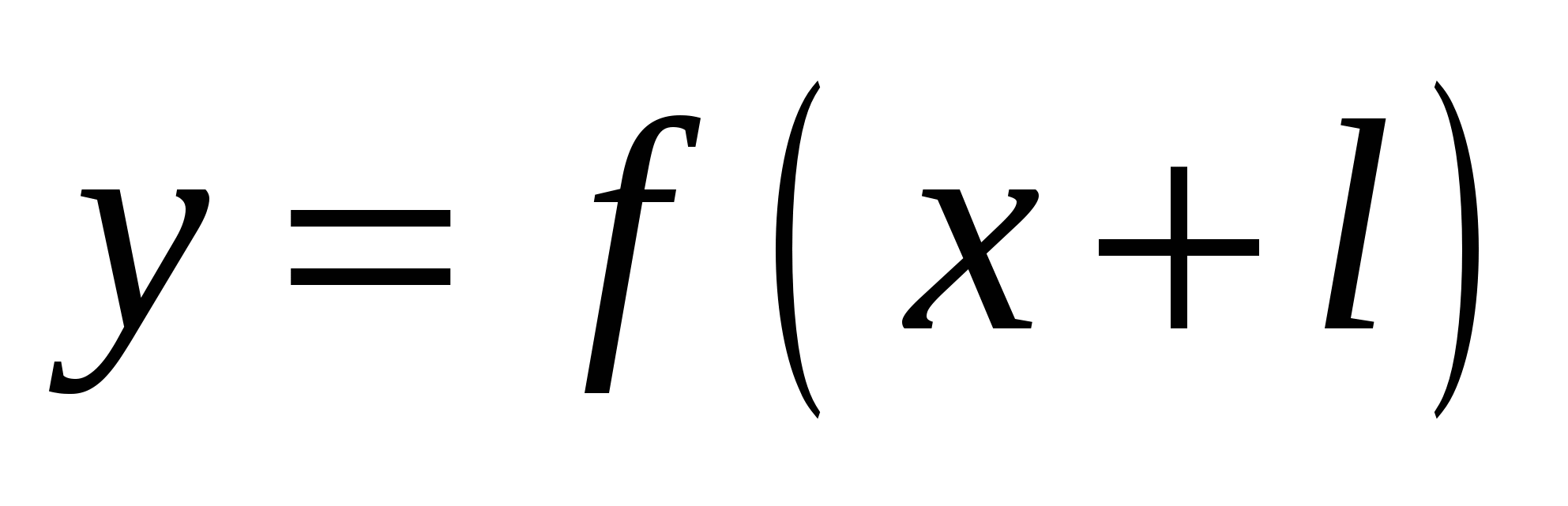ть график функции . Уметь по алгоритму построить график функции 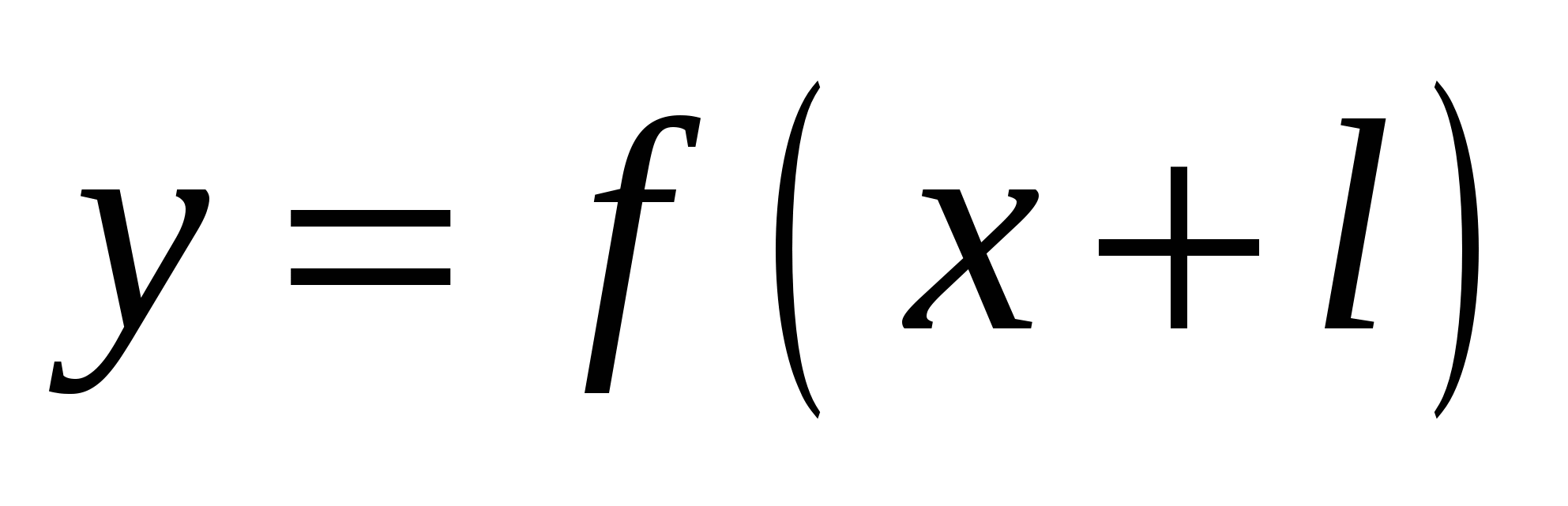, читать и описывать
свойства графика, уверенно действовать в нетиповой, незнакомой ситуации, самостоятельно исправляя допущенные ошибки или неточности.
|
48-49
|
Как построить график функции 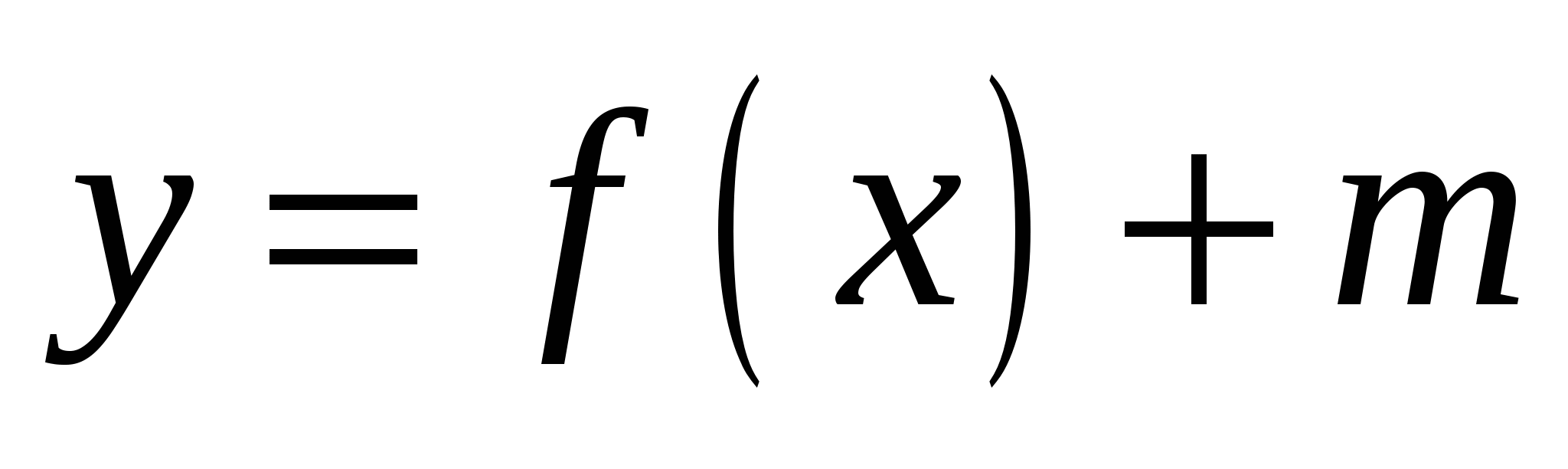 , если известен график функции
|
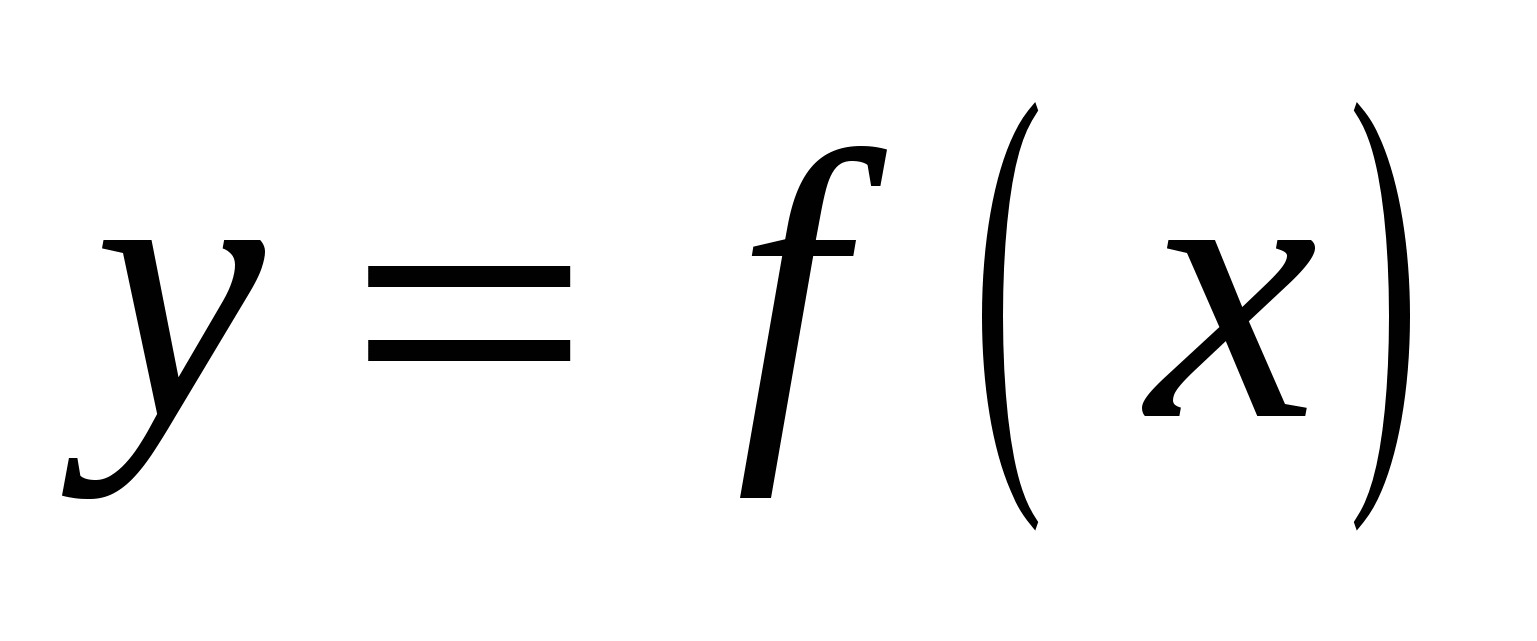
2
|
Иметь представление, как с помощью параллельного переноса вверх или вниз 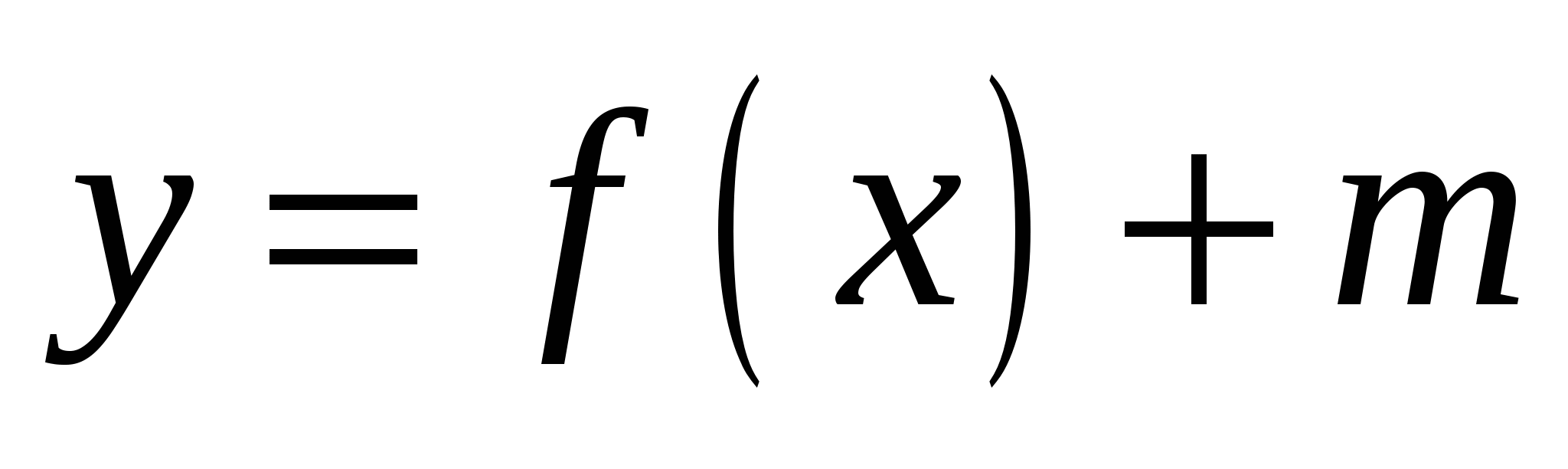построить график функции . Уметь по алгоритму построить график функции 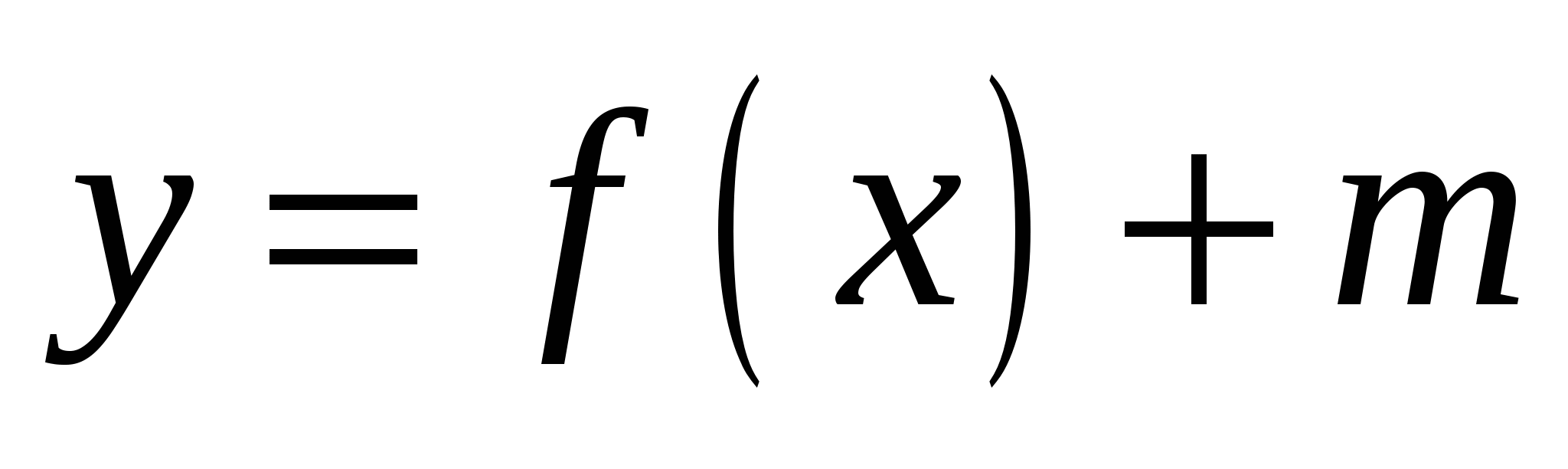, прочитать его и описать свойства функции, принять участие в диалоге, подобрать аргументы для объяснения ошибки.
|
50-51
|
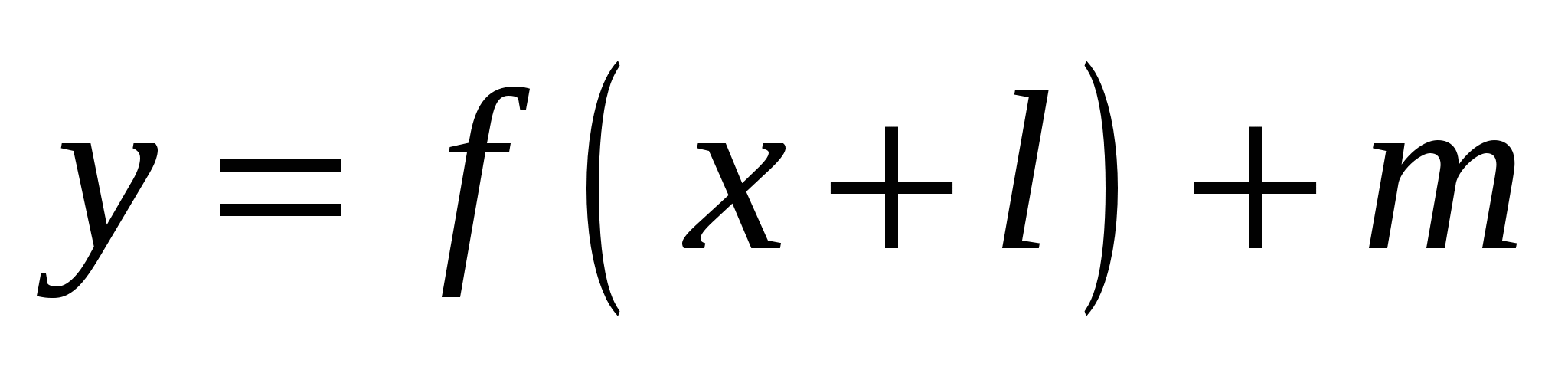Как построить график функции  , если известен график функции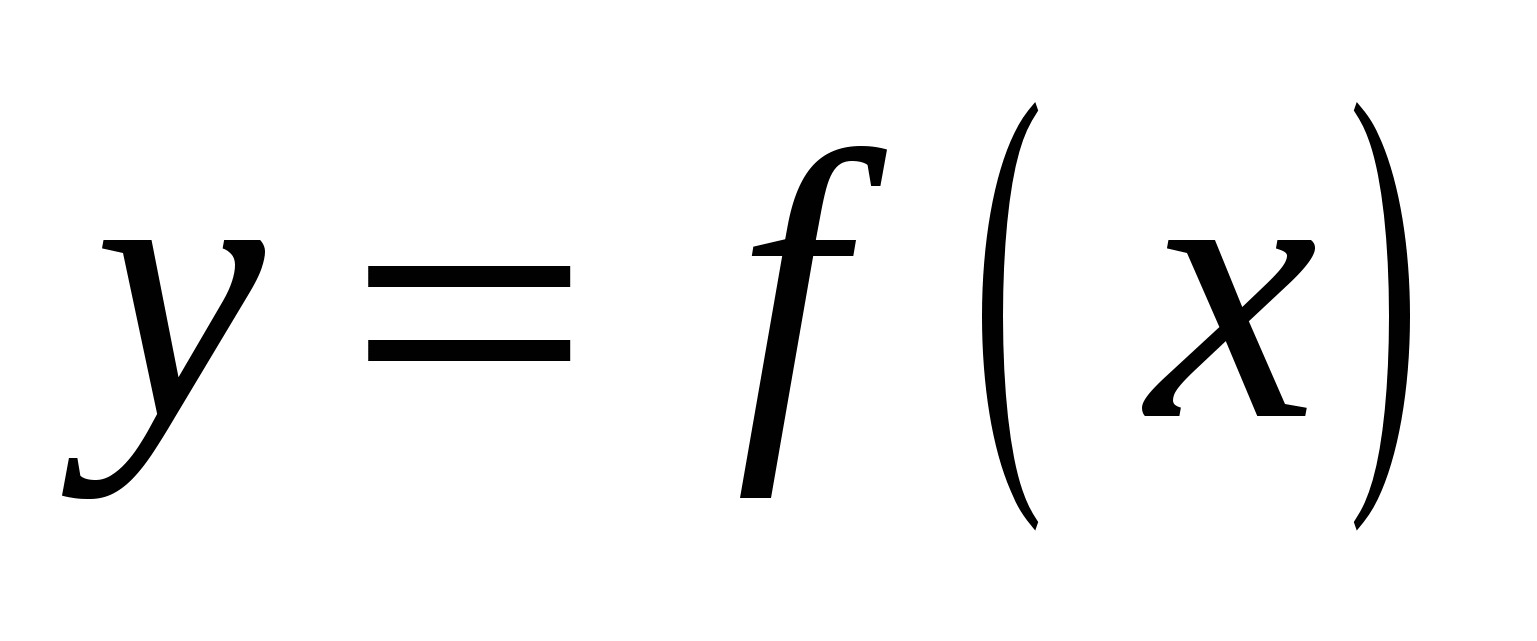
|
2
|
Иметь представление, как с помощью параллельного переноса вверх или вниз построить график функции у = f(x + l) + m . Уметь по алгоритму построить график функции у = f(x + l) + m , прочитать его
и описать свойства функции.
Уметь строить кусочно-заданные функции, осуществлять проверку выводов, положений, закономерностей, теорем.
|
52-54
|
Функция 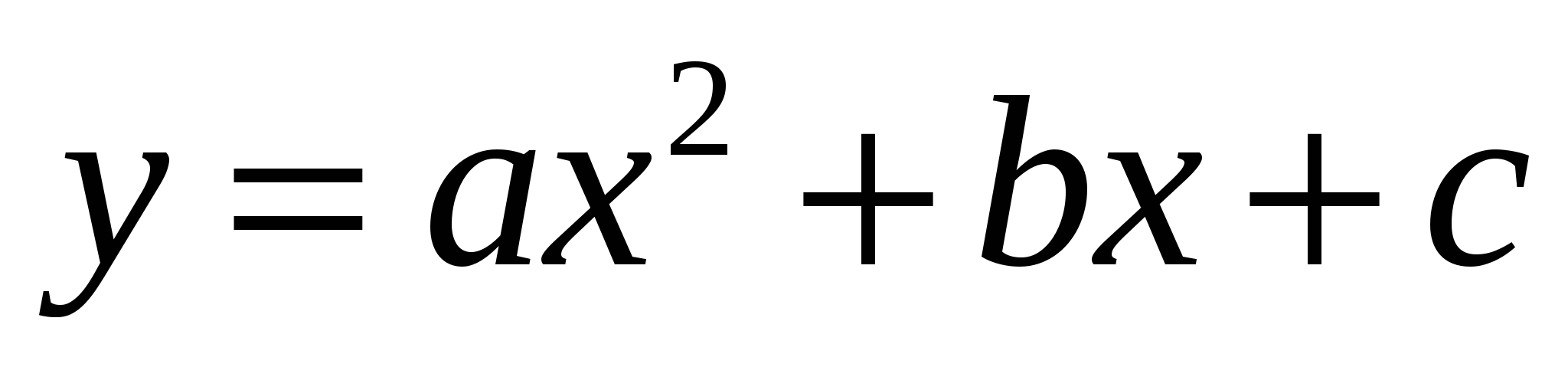 , ее свойства и график
|
3
|
Иметь представление о функции 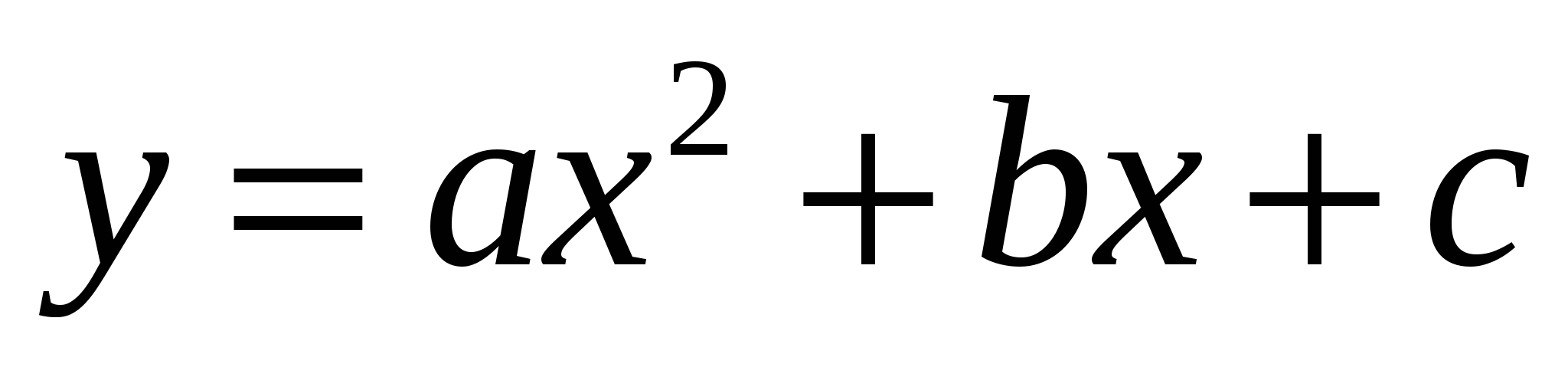, ее графике и свойствах.
Уметь переходить с языка формул на язык графиков и наоборот, определять число корней уравнения и системы уравнений, приводить примеры, подбирать аргументы, формулировать выводы.
|
55-56
|
Графическое решение квадратных уравнений
|
2
|
Знать способы решения квадратных уравнений, применяют их на практике.
Уметь свободно применять несколько способов графического решения уравнений, формировать вопросы, задачи, создавать проблемную ситуацию.
|
57
|
Контрольная работа № 5
|
1
|
Квадратные уравнения
Цель:
- иметь представление о квадратном уравнении, о старшем коэффициенте, втором коэффициенте, о свободном члене, о приведенном квадратном уравнении, полном квадратном уравнении, неполном квадратном уравнении, о корне квадратного уравнения, дискриминанте квадратного уравнения;
овладеть умениями:
- овладеть умениями: решать квадратные уравнения;
- овладеть умениями: выводить формулы корней квадратного уравнения;
- применять правила решения квадратного уравнения: полного, неполного и приведенного
|
58-59
|
Основные понятия
|
2
|
Распознавать линейные и квадратные уравнения, целые и дробные уравнения.
Решать квадратные уравнения, а также уравнения, сводящиеся к ним; решать дробно-рациональные уравнения.
Иметь представление о полном и неполном квадратном уравнении, о решении неполного квадратного уравнения.
Исследовать квадратные уравнения по дискриминанту и коэффициентам.
Решать текстовые задачи алгебраическим способом: переходить от словесной формулировки условия задачи к алгебраической модели путем составления уравнения; решать составленное уравнение; интерпретировать результат.
|
60-62
|
Формулы корней квадратного уравнения
|
3
|
63-65
|
Рациональные уравнения
|
3
|
66
|
Контрольная работа № 6
|
1
|
67-70
|
Рациональные уравнения, как математические модели реальных ситуаций
|
4
|
Иметь представление о теореме Виета и об обратной теореме Виета, о симметрических выражениях с двумя переменными. Уметь составлять квадратные уравнения по их корням, раскладывать на множители квадратный трехчлен, составлять конспект, проводить сравнительный анализ, сопоставлять, рассуждать.
Уметь, не решая квадратного уравнения, вычислять выражения, содержащие корни этого уравнения в виде неизвестных, применяя обратную теорему Виета; обосновывать суждения, давать определения, приводить доказательства, примеры.
Знают, как решать иррациональные уравнения методом возведения в квадрат обеих частей уравнения, применяя свойства равносильных преобразований. Уметь решать иррациональные уравнения, совершая равносильные переходы в преобразованиях, проверять корни, получившиеся при неравносильных преобразованиях
|
71-72
|
Еще одна формула корней квадратного уравнения
|
2
|
73-74
|
Теорема Виета
|
2
|
75
|
Контрольная работа № 7
|
1
|
76-78
|
Иррациональные уравнения
|
3
|
Неравенства
Цель:
- иметь представление о свойстве числовых неравенств, о неравенствах одинакового смысла, неравенствах противоположного смысла, о среднем арифметическом, среднем геометрическом, неравенстве Коши;
овладеть умениями: решения линейных неравенств с одной переменной; решения системы линейных неравенств; применения метода интервалов для решения квадратных неравенств.
|
79-81
|
Свойства числовых неравенств
|
3
|
Формулировать свойства числовых неравенств, иллюстрировать их на координатной прямой, доказывать алгебраически; применять свойства неравенств при решении задач.
Распознавать линейные неравенства. Решать линейные неравенства, системы линейных неравенств.
Приводить примеры конечных и бесконечных множеств. Находить объединение и пересечение множеств.
Приводить примеры несложных классификаций.
Имеют представление о возрастающей, убывающей, монотонной функции на промежутке.
Исследуют и строят различные функции на монотонность, решать уравнения, используя свойство монотонности, осуществляют проверку выводов, положений, закономерностей, теорем.
и исследовать на монотонность функции: линейную, квадратную, обратной пропорциональности, функцию корня.
Исследуют кусочно-заданные функции на монотонность, решать уравнения и неравенства, используя свойство монотонности, составлять конспект, проводить сравнительный анализ, сопоставлять, рассуждать.
Использовать теоретико-множественную символику и язык при решении задач в ходе изучения различных разделов курса.
Иллюстрировать математические понятия и утверждения примерами. Использовать примеры и контр примеры в аргументации.
Конструировать математические предложения с помощью связок если ..., то ..., в том и только том случае, логических связок и, или.
Находить, анализировать, сопоставлять числовые характеристики объектов окружающего мира.
Использовать разные формы записи приближенных значений; делать выводы о точности приближения по записи приближенного значения.
Выполнять вычисления с реальными данными.
Выполнять прикидку и оценку результатов вычислений.
|
82-84
|
Исследование функций на монотонность
|
3
|
85-86
|
Решение линейных неравенств
|
2
|
87-89
|
Решение квадратных неравенств
|
3
|
90
|
Контрольная работа № 8
|
1
|
91-92
|
Приближенные значения действительных чисел, погрешность приближения, приближение по недостатку и избытку
|
2
|
93
|
Стандартный вид числа
|
1
|
94-97
|
Решение задач
|
4
|
Знать материал, изученный в курсе математики за 8 класс
Уметь применять полученные знания на практике.
Уметь логически мыслить, отстаивать свою точку зрения и выслушивать мнение других, работать в команде.
|
98
|
Итоговая контрольная работа
|
1
|
99-102
|
Теория вероятности
|
4
|
Извлекать информацию из таблиц и диаграмм, выполнять вычисления по табличным данным. Определять по диаграммам наибольшие и наименьшие данные, сравнивать величины.
Представлять информацию в виде таблиц, столбчатых и круговых диаграмм, в том числе с помощью компьютерных программ.
Приводить содержательные примеры использования средних для описания данных (уровень воды в водоеме, спортивные показатели, определение границ климатических зон)
|
|
Итого часов
|
102
|
| |
|
|
Скачать 2.09 Mb.