Программа основного общего образования по математике. Математика 5-6, Алгебра 7-9 А. Г. Мордкович
 Скачать 2.09 Mb. Скачать 2.09 Mb.
|
| Программа основного общего образования по математике. Математика 5-6, Алгебра 7-9 А.Г.Мордкович Геометрия 7-9 Л.С.Атанасян 1. Пояснительная записка Программа составлена в соответствии с требованиями Федерального государственного образовательного стандарта второго поколения основного общего образования, примерной программы основного общего образования по математике. Серия «Стандарты второго поколения». Программа подготовлена в рамках проекта «Разработка, апробация и внедрение Федеральных государственных стандартов общего образования второго поколения», реализуемого Российской академией образования по заказу Министерства образования и науки Российской Федерации и Федерального агентства по образованию. Руководители проекта: вице- президент РАО А.А. Кузнецов, академик - секретарь Отделения общего образования РАО М.В. Рыжаков, член президиума РАО А.М. Кандаков; базисного учебного плана образовательного учреждения на 2013-2017 уч/года и обеспечена УМК для 5–9-го классов автора А.Г. Мордкович и др., УМК 7-9-го классов автор Л.С. Атанасян, В.Ф.Бутузов, С.Б.Кадомцев. Математика является одним из основных, системообразующих предметов школьного образования. Такое место математики среди школьных предметов обусловливает и её особую роль с точки зрения всестороннего развития личности учащихся. В основу настоящей программы положены педагогические и дидактические принципы (личностно ориентированные; культурно - ориентированные; деятельностно - ориентированные и т.д.) вариативного развивающего образования, и современные дидактико-психологические тенденции, связанные с вариативным развивающим образованием и требованиями ФГОС. Личностно ориентированные принципы: принцип адаптивности; принцип развития; принцип комфортности процесса обучения. Культурно - ориентированные принципы: принцип целостной картины мира; принцип целостности содержания образования; принцип систематичности; принцип смыслового отношения к миру; принцип ориентировочной функции знаний; принцип опоры на культуру как мировоззрение и как культурный стереотип. Деятельностно - ориентированные принципы: принцип обучения деятельности; принцип управляемого перехода от деятельности в учебной ситуации к деятельности в жизненной ситуации; принцип перехода от совместной учебно-познавательной деятельности к самостоятельной деятельности учащегося (зона ближайшего развития); принцип опоры на процессы спонтанного развития; принцип формирования потребности в творчестве и умений творчества. Программа задает перечень вопросов, которые подлежат обязательному изучению в основной школе. Она так же является логическим продолжением курса математики начальной школы (принцип преемственности). В основе курса лежит авторская идея А.Г.Мордковича; программа позволяет обеспечивать формирование как предметных умений, так и универсальных учебных действий школьников; программа позволяет обеспечивать достижение целей в направлении личностного развития, в метапредметном направлении и предметном направлении. Обучение математике в основной школе направлено на достижение следующих целей:
Целью изучения курса математики в 5-6 классах является систематическое развитие понятия числа, выработка умений выполнять устно и письменно арифметические действия над числами, переводить практические задачи на язык математики, подготовка учащихся к изучению систематических курсов алгебры и геометрии. Курс строится на индуктивной основе с привлечением элементов дедуктивных рассуждений. В ходе изучения курса учащиеся развивают навыки вычислений с натуральными числами, овладевают навыками с обыкновенными и десятичными дробями, положительными и отрицательными числами, получают представление об использовании букв для записи выражений и свойств арифметических действий, составлении уравнений, продолжают знакомство с геометрическими понятиями, приобретают навыки построения геометрических фигур. Целью изучения курса алгебры в 7 - 9 классах является развитие вычислительных умений до уровня, позволяющего уверенно использовать их при решении задач математики и смежных предметов, усвоение аппарата уравнений и неравенств как основного средства математического моделирования задач, осуществление функциональной подготовки школьников. Курс характеризуется повышением теоретического уровня обучения, постепенным усилием роли теоретических обобщений и дедуктивных заключений. Прикладная направленность раскрывает возможность изучать и решать практические задачи. Целью изучения курса геометрии в 7-9 классах является систематическое изучение свойств геометрических фигур на плоскости, формирование пространственных представлений, развитие логического мышления и подготовка аппарата, необходимого для изучения смежных дисциплин и курса стереометрии в старших классах. В основе построения данного курса лежит идея гуманизации обучения, соответствующая современным представлениям о целях школьного образования и уделяющая особое внимание личности ученика, его интересам и способностям. Предлагаемый курс позволяет обеспечить формирование, как предметных умений, так и универсальных учебных действий школьников, а также способствует достижению определённых во ФГОС личностных результатов, которые в дальнейшем позволят учащимся применять полученные знания и умения для решения различных жизненных задач. 2. Общая характеристика учебного предмета «Математика» Настоящая программа основного общего образования по математике составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам общего образования, представленных в федеральном государственном образовательном стандарте общего образования, с учетом преемственности с Примерными программами для начального общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования. Содержание математического образования применительно к основной школе представлено в виде следующих содержательных разделов. Это арифметика; алгебра; функции; вероятность и статистика; геометрия. Наряду с этим в содержание основного общего образования включены два дополнительных методологических раздела: логика и множества; математика в историческом развитии, что связано с реализацией целей общеинтеллектуального и общекультурного развития учащихся. Содержание каждого из этих разделов разворачивается в содержательно-методическую линию, пронизывающую все основные разделы содержания математического образования на данной ступени обучения. При этом первая линия — «Логика и множества» — служит цели овладения учащимися некоторыми элементами универсального математического языка, вторая — «Математика в историческом развитии» — способствует созданию общекультурного, гуманитарного фона изучения курса. Содержание раздела «Арифметика» служит базой для дальнейшего изучения учащимися математики, способствует развитию их логического мышления, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. Развитие понятия о числе в основной школе связано с рациональными и иррациональными числами, формированием первичных представлений о действительном числе. Завершение числовой линии (систематизация сведений о действительных числах, о комплексных числах), так же как и более сложные вопросы арифметики (алгоритм Евклида, основная теорема арифметики), отнесено к ступени общего среднего (полного) образования. Содержание раздела «Алгебра» способствует формированию у учащихся математического аппарата для решения задач из разных разделов математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей процессов и явлений реального мира. В задачи изучения алгебры входят также развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики, овладение навыками дедуктивных рассуждений. Преобразование символьных форм вносит специфический вклад в развитие воображения учащихся, их способностей к математическому творчеству. В основной школе материал группируется вокруг рациональных выражений, а вопросы, связанные с иррациональными выражениями, с тригонометрическими функциями и преобразованиями, входят в содержание курса математики на старшей ступени обучения в школе. Содержание раздела «Функции» нацелено на получение школьниками конкретных знаний о функции как важнейшей математической модели для описания и исследования разнообразных процессов. Изучение этого материала способствует развитию у учащихся умения использовать различные языки математики (словесный, символический, графический), вносит вклад в формирование представлений о роли математики в развитии цивилизации и культуры. Раздел «Вероятность и статистика» — обязательный компонент школьного образования, усиливающий его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования у учащихся функциональной грамотности — умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах. При изучении статистики и вероятности обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления. Цель содержания раздела «Геометрия» — развить у учащихся пространственное воображение и логическое мышление путем систематического изучения свойств геометрических фигур на плоскости и в пространстве и применения этих свойств при решении задач вычислительного и конструктивного характера. Существенная роль при этом отводится развитию геометрической интуиции. Сочетание наглядности со строгостью является неотъемлемой частью геометрических знаний. Материал, относящийся к блокам «Координаты» и «Векторы», в значительной степени несет в себе межпредметные знания, которые находят применение как в различных математических дисциплинах, так и в смежных предметах. Особенностью раздела «Логика и множества» является то, что представленный в нем материал преимущественно изучается при рассмотрении различных вопросов курса. Соответствующий материал нацелен на математическое развитие учащихся, формирование у них умения точно, сжато и ясно излагать мысли в устной и письменной речи. Раздел «Математика в историческом развитии» предназначен для формирования представлений о математике как части человеческой культуры, для общего развития школьников, для создания культурно-исторической среды обучения. На него не выделяется специальных уроков, усвоение его не контролируется, но содержание этого раздела органично присутствует в учебном процессе как своего рода гуманитарный фон при рассмотрении проблематики основного содержания математического образования. Данная программа по математике для основной школы является логическим продолжением программы для начальной школы и вместе с ней составляет описание непрерывного курса математики с 1-го по 9-й класс общеобразовательной школы. 3.Место предмета «Математика» в учебном плане. В соответствии с требованиями Федерального государственного образовательного стандарта основного общего образования предмет «Математика» изучается с 5-го по 9-й класс в виде следующих учебных курсов: 5–6 класс – «Математика», 7–9 класс – «Алгебра» и «Геометрия». Общее количество уроков в неделю с 5 по 9 класс составляет 25 часов (5–6 класс – по 5 часов в неделю, 7–9 класс – алгебра по 3 часа в неделю, геометрия – по 2 часа в неделю.) Распределение учебного времени между этими предметами представлено в таблице.
4. Личностные, метапредметные и предметные результаты освоения учебного предмета «Математика» Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы. Обучение математике в основной школе направлено на достижение следующих результатов:
Взаимосвязь результатов освоения предмета «Математика» можно системно представить в виде схемы. При этом обозначение ЛР указывает, что продвижение учащихся к новым образовательным результатам происходит в соответствии с линиями развития средствами предмета. 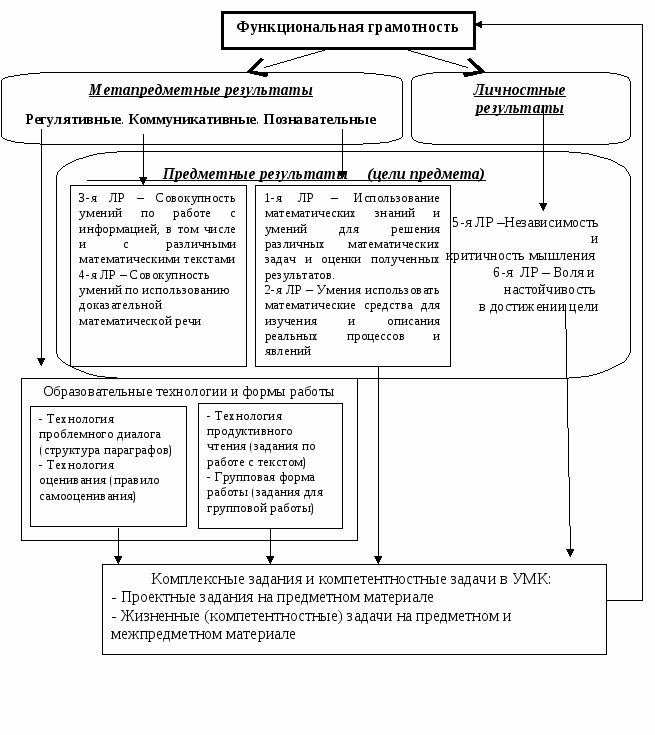 | ||||||||||||||