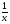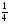Решение задач с помощью дробно-рациональных уравнений
 Скачать 76.85 Kb. Скачать 76.85 Kb.
|
| Логинова Алевтина Владимировна учитель математики МБОУ Березовская СОШ ХМАО Тюменской области Класс: 8 Тема урока: Решение задач с помощью дробно-рациональных уравнений. Слайд 1. Урок обобщения знаний. Деятельностная цель: формирование способности учащихся обобщать и систематизировать знания при решении задач с помощью рациональных уравнений. Образовательная цель: отработка навыков работы составления уравнений по условию задач. Задачи: Образовательные: выработать умение решать задачи с помощью дробно – рациональных уравнений. Развивающие: вовлечь в активную практическую деятельность, совершенствовать навыки общения. Воспитательные: формирование уважительного отношения к малой Родине, чувства патриотизма к родной земле, желания трудиться на ней и приносить пользу. Личностные УУД: ценностное отношение к умению удерживать учебную задачу, осознание учащимися практической и личностной значимости результатов каждого этапа урока, ответственное отношение к результатам своей деятельности. Регулятивные УУД: умение принимать и сохранять цель урока, умение планировать, контролировать и оценивать свои действия, умение провести рефлексию своих действий на уроке. Коммуникативные УУД: умение слушать собеседника и вести диалог, высказывать свою точку зрения, правильно говорить, умение преодолевать трудности в учении, используя для этого проблемную ситуацию, умение анализировать, сравнивать, обобщать изучаемый материал. Используемое оборудование: интерактивная доска, учебник «Алгебра» 8 класс «Просвещение» авторы Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова, под редакцией С.А.Теляковского. Ход урока. Вступительное слово учителя. Здравствуйте, ребята! Сегодняшний урок будет посвящён решению текстовых задач. Жизнь вообще перед нами ставит множество задач. Не все они решаются алгебраическим способом, но научившись решать математические задачи, вы сможете всегда прийти к верному решению какой – либо проблемы. На уроке мы посетим некоторые предприятия нашего поселка Березово и попробуем решить ряд производственных задач, которые возникают перед их работниками. Слайд 2. Стадия вызова. С помощью каких типов задач можно решать эти проблемы? Что же все эти задачи объединяет? (Учитель записывает варианты ответов.) В конце урока мы снова попытаемся ответить на этот вопрос. Для успешного решения алгебраических задач необходимо знать многие математические понятия. Актуализация. Слайд 3. Каждая группа должна составить кластер: «Что надо знать для того, чтобы решить задачу?» В течение 3 минут вы будете составлять кластер, отвечая на этот вопрос. Какая группа за 3 минуты перечислит как можно больше понятий, связанных с темой «ЗАДАЧА», тот выиграет этот конкурс. (Оценивает сам учитель: 5 баллов - каждому из группы победителей и 4 балла остальным). Проверка кластеров. Слайд 4. Помним цель нашего урока! У нас с вами уже накоплен опыт по решению текстовых задач, как правило, они решаются с помощью… Ученик: уравнений. Что такое уравнение? Ученик: Уравнение-равенство, содержащее переменную. Как называются уравнения, которыми мы последнее время используем на уроках? Ученик: Дробно-рациональные уравнения. Чем они отличаются от уравнений другого класса? Ученик: Тем, что переменная стоит в знаменателе. Поэтому, что надо учитывать при решении рациональных уравнений? Ученик: ОДЗ. Слайд 5. А мы сегодня затронем 3 вида задач: на работу, на движение и на концентрацию. Каждой группе достанется один из этих видов. Практическая работа. Представитель от каждой группы, назовем его - ДОВЕРЕННОЕ ЛИЦО, выходит и делает свой выбор. Доверенные лица вытягивают карточки с надписями: «Технологи »; « Предприниматели», «Дальнобойщики». Каждая группа получает задачу, и оформляют решение на плакатах. Они могут воспользоваться памятками при оформлении решения задач для защиты. Технологи. В лаборатории Березовского рыбоконсервного комбината в водный раствор соли, предназначенный для засолки рыбы «сырок» добавили 100 г воды. В результате концентрация соли в растворе понизилась на 1%. Определите первоначальную массу раствора, если известно, что в нем содержалось 30 г соли. Слайд 6. Решение. Пусть было x (г) раствора, тогда концентрация соли в растворе 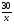 ·100%. После добавления 100 г воды, масса раствора стала x+100 (г) и концентрация соли ·100%. После добавления 100 г воды, масса раствора стала x+100 (г) и концентрация соли  ·100%. По условию задачи ·100%. По условию задачи 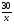 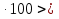  ·100% на 1%. По смыслу задачи x ·100% на 1%. По смыслу задачи x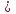 0.Составим уравнение: 0.Составим уравнение: 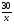 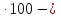  ·100% =1%. ·100% =1%. 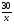   =0,01; ОДЗ: x =0,01; ОДЗ: x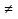 0; x 0; x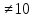 0. 0.30(x+100) – 30x =0,01x(x+100); 30x+3000 – 30x =0,01 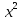 +x; +x;0,01 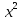 +x – 3000=0; +x – 3000=0;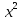 +100x – 300000=0; +100x – 300000=0;D= 2500+300000=302500=  ; ;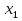 =-50-550=-600-не удовлетворяет условию задачи; =-50-550=-600-не удовлетворяет условию задачи;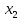 =-50+550=500 =-50+550=500Ответ: 500 г. Предприниматели. Две швейные мастерские «Шторы» и «Татьяна» получили заказ на пошив оконных штор. Известно, что мастерская «Шторы» на выполнение заказа затрачивает на 6 часов больше, чем мастерская «Татьяна». За сколько часов может выполнить это задание каждая мастерская, если при совместной работе им потребуется для этого 4 часа? Слайд 7. Решение.
По смыслу задачи x 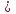 0 0Составим уравнение: 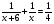 ; ОДЗ: x ; ОДЗ: x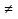 0; x 0; x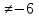 . .4x + 4(x+6) = x(x+6); 4x + 4x + 24 = 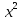 + 6x; + 6x;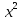 - 2x – 24 = 0; - 2x – 24 = 0;D = 25; 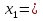 6; 6;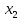 = - 4 – не удовлетворяет условию задачи. = - 4 – не удовлетворяет условию задачи.Ответ: 4 и 6 часов. Дальнобойщики. Две фуры выезжают одновременно из п. Березова в Ханты-Мансийск. Скорость первого на 10 км/ч больше скорости второго, и поэтому первый автомобиль приезжает на место на 1 час раньше второго. Найдите скорость каждого автомобиля, зная, что расстояние между городами равно 560 км. Слайд 8. Решение.
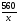 > > на 1. По смыслу задачи x на 1. По смыслу задачи x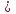 0. 0.Составим уравнение: 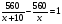 ; ОДЗ: x ; ОДЗ: x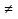 0; x 0; x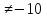 . .560x - 560(x+10) = x(x+10); 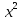 + 10x +5600 = 0; + 10x +5600 = 0;D = 5625; 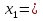 70; 70;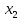 = - 80 – не удовлетворяет условию задачи. = - 80 – не удовлетворяет условию задачи.Ответ: 70 и 80 км/ч. Время выполнения -12 минут. Оценивает меру участия каждого члена в решении задачи - доверенное лицо по 5 бальной системе. Перед защитой проведем физкультминутку. Поза «Квазимоды»: поднять плечи максимально вверх, подержать немного и опустить. Затем свободное вращение головой в одну и другую сторону. Упражнение для лица: сильно нахмуриться (свести брови), задержаться и расслабиться. Сильно удивиться (поднять брови), задержаться и расслабиться. Максимально широко улыбнуться, задержать «улыбку» и расслабиться. Защита решенных задач. Переходим к защите решенных задач. Слушая выступление доверенного лица, попытайтесь составить схему уравнения через обозначение величин. Оценка выступления выставляется группами после обсуждения. Максимальный балл – 5. В ходе обсуждения приходим к выводу: «Все рассмотренные нами задачи имеют одинаковую математическую модель». Рефлексия. Вы сегодня хорошо потрудились и оказались в роли работников предприятий нашего родного поселка и увидели, как ваш математический опыт может пригодиться в жизненных ситуациях. А теперь подведите итог и к каждой букве слова «модель» подберите существительные, которые были использованы на уроке и отражали бы математические понятия по теме нашего урока. Количество баллов равно количеству записанных слов. Оценочные листы и слова сдаются учителю. Слайд 9. Домашнее задание. На оценку «5»: № 714, 715; на оценку «4»: № 714. Задание на «любителя»: составить по уравнению задачу: 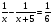 . Слайд 10. . Слайд 10.Каждый учащийся сдает свой оценочный лист учителю для выставления результата работы в журнал. Оценочный лист ФИ учащегося
«5» - 18 - 20 баллов; «4» - 14 - 17 баллов; «3» - 10 - 13 баллов. |