|
Закономерности окружающего мира 7 класс Тема Алгебра событий и основные правила вычисления вероятностей
 Закономерности окружающего мира – 7 класс
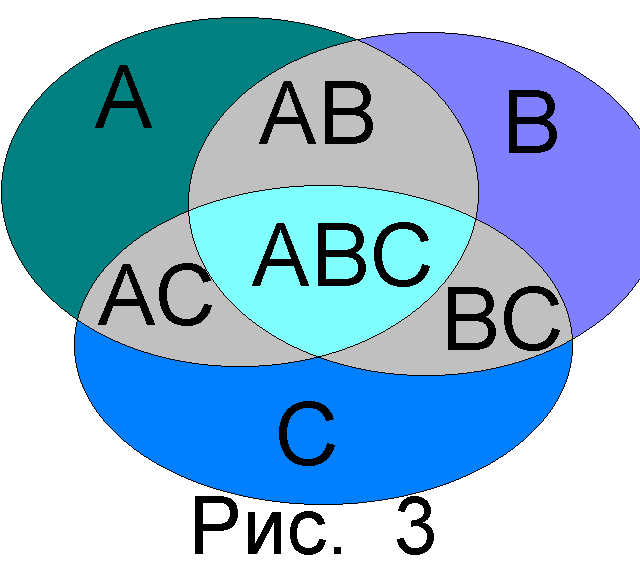
Тема 9. Алгебра событий и основные правила вычисления вероятностей.
урок на тему Правило сложения вероятностей несовместных событий
задачи урока: познакомить школьников с основными правилами вычисления вероятностей
оборудование урока: таблицы по математике, иллюстрирующие правила сложения
содержание урока:
Организация школьников на урок.
Изучение нового материала:
Формула включения – исключения.
Вероятность суммы двух событий равна сумме вероятностей этих событий без вероятности их совместного наступления
-
P(A+B) = P(A) + P(B) - P(AB)
|
Для случая трех событий
-
P(A+B+С) = P(A)+P(B)+P(C)-P(AB)-P(AC)-P(BC)+P(ABC)
|
ПРИМЕР. Опыт состоит в случайном извлечении карты из колоды в 52 карты. Чему равна вероятность того, что это будет или туз, или карта масти треф?
|
Решение.
Определим события: А - "Извлечение туза", В - "Извлечение карты трефовой масти". Р(А) = 4/15, Р(В) = 13/52; вероятность их пересечения - извлечение трефового туза - Р(АВ) = 1/52.
Событие B ->
|
Треф
|
Бубны
|
Пики
|
Червы
|
Туз
|
Туз
|
Туз
|
Туз
|
Король
Дама
Валет
10
...
2
|
Король
Дама
Валет
10
...
2
|
Король
Дама
Валет
10
...
2
|
Король
Дама
Валет
10
...
2
|
|
|
Нас интересует вероятность суммы событий А и В.
P(A+B) = 4/52 + 13/52 - 1/52 = 16/52 = 1/2.
|
Ответ:
1/2.
|
|
|
|
Несовместные события.
Два события называются несовместными, если они не пересекаются.
Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий.
Для несовместных событий А, В
P(A+B) = P(A) + P(B)
|
Правило сложения вероятностей справедливо и для конечного числа n попарно несовместных событий
P(A1+A2+A3+...+An) = P(A1) + P(A2) + P(A3) +...+P(An)
ПРИМЕР.Компания производит 40000 холодильников в год. которые ревлизуются в различных регионах России. Из них 10000 экспортируются в страны СНГ, 8000 продаются в регионах Европейской части России, 7000 продаются в страны дальнего зарубежья, 6000 в Западной Сибири, 5000 в Восточной Сибири, 4000 в Дальневосточном районе. Чему равна вероятность того , что определенный холодильник будет: а)произведен на экспорт; б)продан в России?
|
Решение.
Обозначим события: А - "Холодильник будет продан в странах СНГ";
Р(А) = 10000/40000 = 0,25;
В - "Холодильник будет продан в Европейской части России";
P(B) = 8000/40000 = 0,2;
С - "Холодильник будет продан в страны дальнего зарубежья";
P(C) = 7000/40000 = 0/175;
D - "Холодильник будет продан в Восточной Сибири";
P(D) = 6000/40000 = 0,15;
E - "Холодильник будет продан в Западной Сибири";
P(E) = 5000/40000 = 0,125;
F - "Холодильник будет продан в Дальневосточном районе"; P(F) = 4000/40000 = 0,1.
События А, B, C, D, E, F - несовместные. а) P(холодильник произведен на экспорт) = P(A+B) = P(A) + P(B) = 0,25 + 0,175 = 0,425.
б )P(холодильник будет продан в России) = P(B+D+E+F) = P(B) + P(D) + P(E) + P(F) = 0,2 + 0,15 + 0,125 + 0,1 = 0,575.
|
Ответ:
P(холодильник произведен на экспорт) = 0,425.
P(холодильник будет продан в России) = 0,575.
|
|
|
|
Закрепление знаний. Решение задач 1,2, с.266
Домашнее задание: п.9.1
|
|
|
Скачать 34.72 Kb.