|
Протокол №1 от «27» августа 20 12 г. «Согласовано» Заместитель директора по увр
«Рассмотрено»
Руководитель ШМО
_____/_Харина Т. П._/
ФИО
Протокол № _1__ от
«_27_» _августа_ 20 12г.
|
«Согласовано»
Заместитель
директора по УВР
МОУ «СОШ № _1_»
______ /_Жигаева Л. А. /
ФИО
«_27_» _августа_ 2012г.
|
«Утверждаю»
Директор
МОУ «СОШ № _1_»
______ /_Кузнецов А.С._/
ФИО
Приказ № _____ о/д__ от
«_31_» _августа_ 20 12г.
|
РАБОЧАЯ ПРОГРАММА
учебного предмета
___________________МОУ СОШ №1__________________
наименование ОУ
Харина Татьяна Павловна , первая
Ф.И.О. учителя, категория
по ____________математике_______________________________
предмет
______________________ 8А,8Б_____________________________
класс
Рассмотрено на заседании
педагогического совета
протокол № __1_____ от
«_31_» __августа___ 2012г.
2012-2013 учебный год
Учебно-тематическое планирование
по математике .
предмет
Классы 8А,8Б
Учитель Харина Татьяна Павловна
Количество часов
Всего 210 час; в неделю 6 час.
Плановых контрольных уроков 15 , тестов 2 ч.;
Административных контрольных уроков 4 ч.
Планирование составлено на основе Программы общеобразовательных учреждений. Алгебра.и геометрия 7-9 классы. Составитель: Бурмистрова Т.А. – М.: Просвещение, 2009 г.
с учетом требований федерального компонента Государственного стандарта общего образования.
.
Учебник Алгебра для 8 кл. общеобразоват. учреждений /Ю.Н,Макарычев, Н,Г,Миндюк и др/
название, автор, издательство, год издания
М.: Просвещение,2011.; Алгебра для 8 кл. общеобразоват. Учреждений( с углубленным изучением математики) /Ю.Н,Макарычев, Н,Г,Миндюк и др/ М.: Просвещение,2011.; Геометрия 7-9 / Л.С.Атанасян, Б.Ф.Бутузов и др./ М: Просвещение,2004.
Дополнительная литература дидактика по геометрии 8 кл./Б.Г.Зив, В.М.Мейлер/, .
название, автор, издательство, год издания
М.: «Просвещение»,2011; дидактический материал по алгебре 8 кл./В.И.Жохов, Ю.Н.Макарычев,Н.Г.МиндюкМ: «Просвещение»2009, дидактический материал по алгебре и геометрии 8кл./А.П.Ершова,В.В.Голобородько/ М.: «Илекса»,2010; КИМы 8 класс Алгебра (Л.Ю. Бабошкина)М.: «ВАКО», 2011
Информационное обеспечение Уроки математики с применением информационных технологий. Методическое пособие с электронным приложением /Л.И.Горохова и др.-2-оеизд., М.: Издательство «Глобус», 2010.
Пояснительная записка
Статус документа
Рабочая программа по математике составлена на основе федерального компонента государственного стандарта основного общего образования.
Данная рабочая программа ориентирована на учащихся 8 классов и реализуется на основе следующих документов:
Федеральный компонент государственного образовательного стандарта начального общего, основного общего и среднего (полного) общего образования (Приказ МО РФ от 05.03.2004 №1089).
Федеральный базисный учебный план для среднего (полного) общего образования .
Примерная программа основного общего образования по математике, «Дрофа», 2004г.
Рабочая программа конкретизирует содержание предметных тем образовательного стандарта и дает примерное распределение учебных часов по разделам курса.
Примерная программа выполняет две основные функции.
Информационно-методическая функция позволяет всем участникам образовательного процесса получить представление о целях, содержании, общей стратегии обучения, воспитания и развития учащихся средствами данного учебного предмета.
Организационно-планирующая функция предусматривает выделение этапов обучения, структурирование учебного материала, определение его количественных и качественных характеристик на каждом из этапов, в том числе для содержательного наполнения промежуточной аттестации учащихся.
Структура документа
Рабочая программа включает три раздела: пояснительную записку; основное содержание с примерным распределением учебных часов по разделам курса; требования к уровню подготовки выпускников.
Общая характеристика учебного предмета
Математическое образование в основной школе складывается из следующих содержательных компонентов (точные названия блоков): арифметика; алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.
Арифметика призвана способствовать приобретению практических навыков, необходимых для повседневной жизни. Она служит базой для всего дальнейшего изучения математики, способствует логическому развитию и формированию умения пользоваться алгоритмами.
Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей реальности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. Одной из основных задач изучения алгебры является развитие алгоритмического мышления, необходимого, в частности, для освоения курса информатики; овладение навыками дедуктивных рассуждений. Преобразование символических форм вносит свой специфический вклад в развитие воображения, способностей к математическому творчеству. Другой важной задачей изучения алгебры является получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов (равномерных, равноускоренных, экспоненциальных, периодических и др.), для формирования у учащихся представлений о роли математики в развитии цивилизации и культуры.
Геометрия – один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Элементы логики, комбинаторики, статистики и теории вероятностей становятся обязательным компонентом школьного образования, усиливающим его прикладное и практическое значение. Этот материал необходим, прежде всего, для формирования функциональной грамотности – умений воспринимать и анализировать информацию, представленную в различных формах, понимать вероятностный характер многих реальных зависимостей, производить простейшие вероятностные расчеты. Изучение основ комбинаторики позволит учащемуся осуществлять рассмотрение случаев, перебор и подсчет числа вариантов, в том числе в простейших прикладных задачах.
При изучении статистики и теории вероятностей обогащаются представления о современной картине мира и методах его исследования, формируется понимание роли статистики как источника социально значимой информации и закладываются основы вероятностного мышления.
Таким образом, в ходе освоения содержания курса учащиеся получают возможность:
развить представления о числе и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
развить пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами;
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
развить логическое мышление и речь – умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Задачи
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельности;
освоение компетенций: учебно-познавательной, коммуникативной, рефлексивной, личностного саморазвития, ценностно-ориентационной и профессионально-трудового выбора.
Место предмета в федеральном базисном учебном плане
Согласно федеральному базисному учебному плану для образовательных учреждений Российской Федерации на изучение математики на ступени основного общего образования в 8 классах отводится 175 ч из расчета 5 ч в неделю.
Рабочая программа является модифицированной. В соответствии с учебным планом на изучение математики в 8 классах выделено 6 часов в неделю, всего 210 ч. (1час в неделю из школьного компонента). Добавленные часы направлены на расширение и углубление некоторых тем программы:
«Рациональные дроби» дополнена 3 часами на изучение темы «Представление дроби в виде суммы дробей».
В главе «Квадратные корни» на изучение темы «Арифметический квадратный корень» дополнительно отводится 3 часа с целью изучения темы «Преобразование двойных радикалов», свойств арифметического квадратного корня.
Глава «Квадратные уравнения» дополнена 13 часами на изучение тем «Уравнения, сводящиеся к квадратным», «Выражения, симметрические относительно корней квадратного уравнения», «Разложение квадратного трехчлена на множители», «Решение уравнений с параметрами», «Решение дробно – рациональных уравнений с параметрами».
При изучении темы «Неравенства с одной переменной и их системы» выделено 2 часа для изучения темы «Решение простейших неравенств с модулем».
На изучение дополнительной главы «Функции и графики» отводится 10 часов.
Дополнительно выделено 4 часа для решения задач по теме «Соотношения между сторонами и углами и углами прямоугольного треугольника» с целью углубления умений и навыков при решении задач, развития творческой и прикладной стороны мышления.
В данном классе ведущими методами обучения предмету являются: поисковый, объяснительно-иллюстративный и репродуктивный. На уроках используются элементы следующих технологий: личностно ориентированное обучение, обучение с применением опорных схем, ИКТ.
Контрольных работ за год – 15. Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных и математических диктантов.
Общеучебные умения, навыки учащихся по математике на начало учебного года.
В результате изучения курса алгебры 7-го класса учащиеся должны уметь:
бегло и уверенно выполнять арифметические действия с рациональными числами; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления;
выполнять тождественные преобразования выражений: приведение подобных слагаемых, раскрытие скобок со знаком «плюс» или «минус» пред скобками;
решать уравнения с одним неизвестным и применять уравнения к решению текстовых задач; решать системы линейных уравнений;
строить графики функций 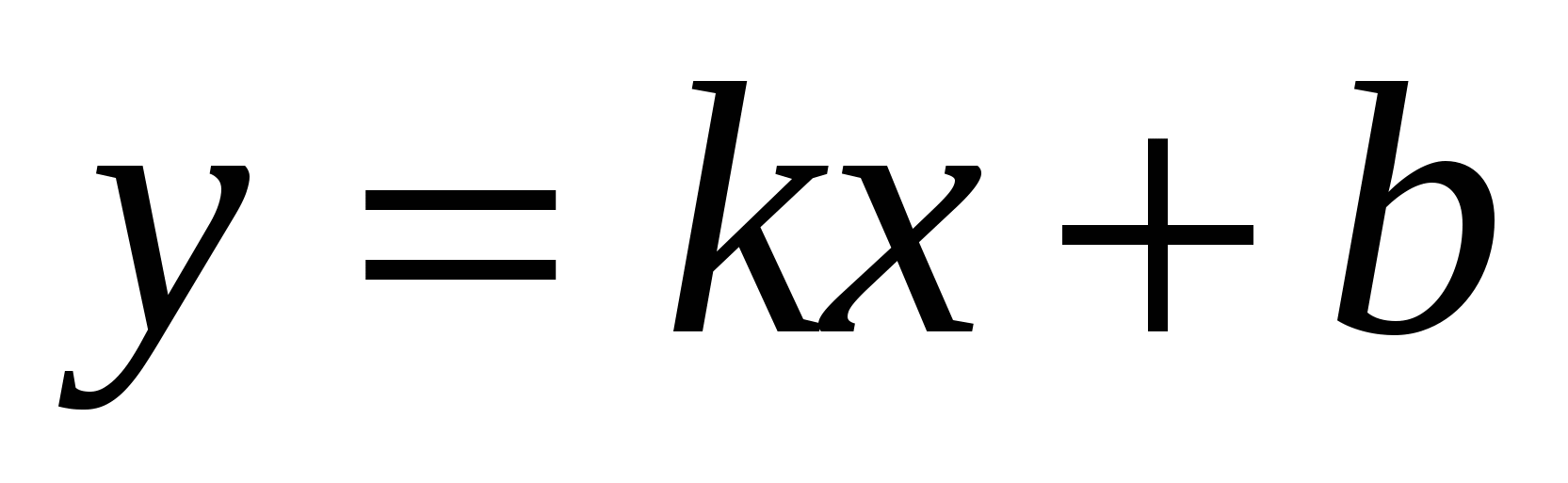 , (b≠0), , (b≠0), 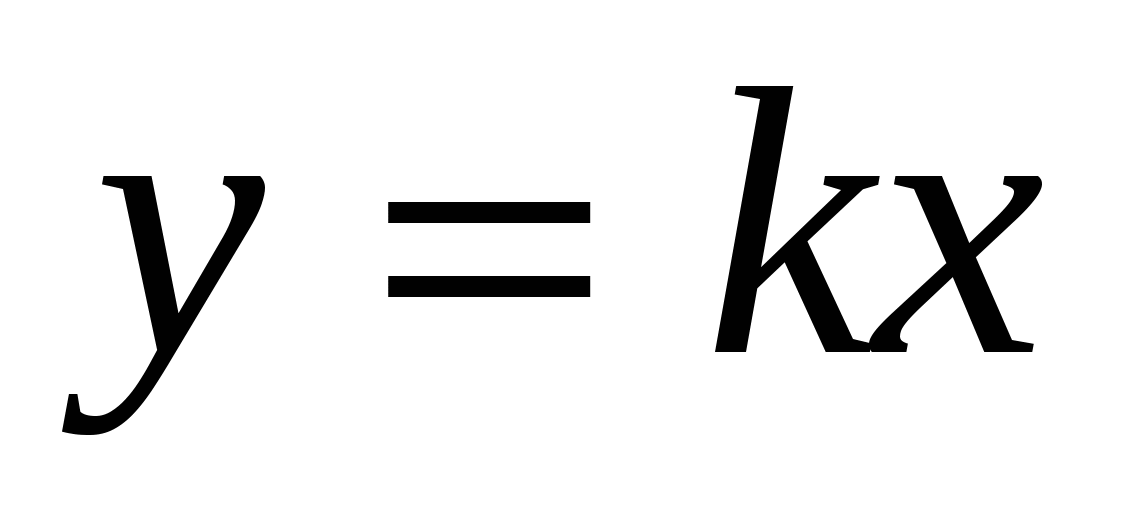 ; понимать как влияет знак коэффициента k на расположение в координатной плоскости графика функции ; понимать как влияет знак коэффициента k на расположение в координатной плоскости графика функции 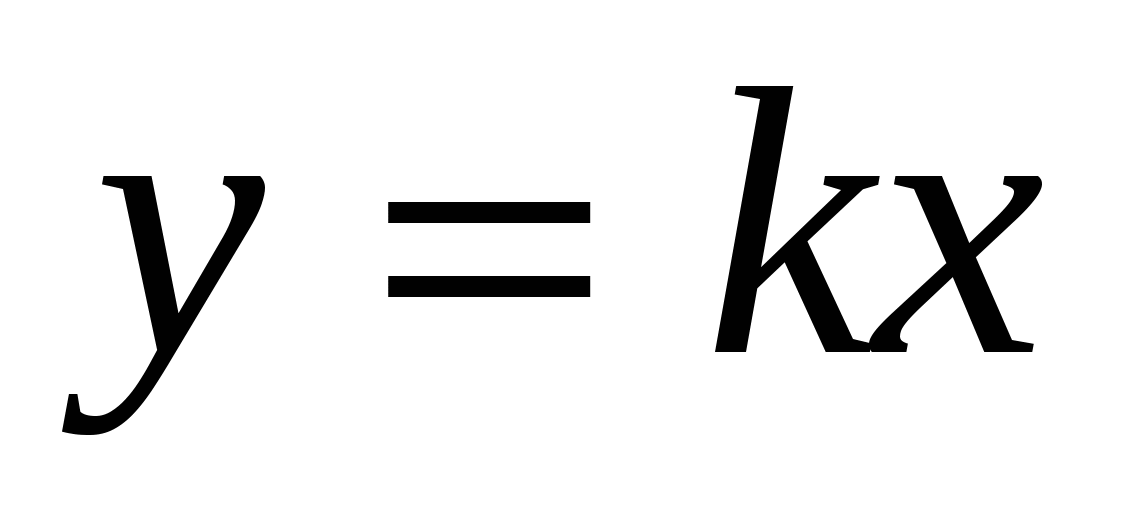 , где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида , где k≠0, как зависит от значений k и b взаимное расположение графиков двух функций вида 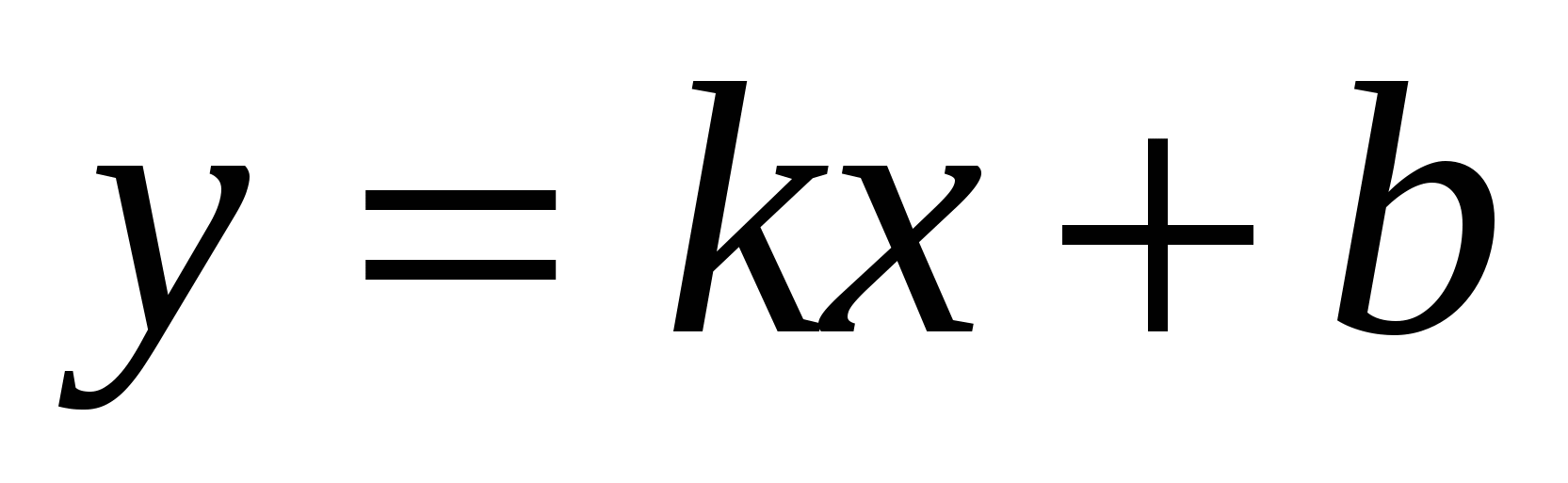 ; видеть эту зависимость, ; видеть эту зависимость,
выполнять основные действия со степенями с натуральным показателем, с многочленами; выполнять разложение многочленов на множители;
понимать графическую интерпретацию решения уравнений и систем уравнений;
понимать содержательный смысл важнейших свойств функции; по графику функции отвечать на вопросы, касающиеся её свойств; строить графики функций – линейной, квадратичной функции и функции 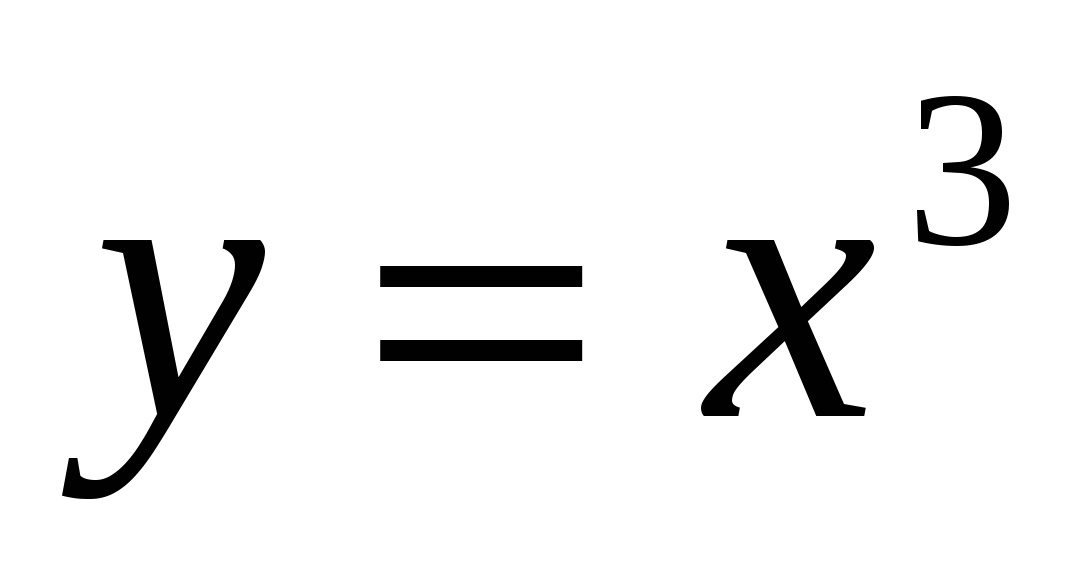 ; ;
использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе с использованием при необходимости справочной литературы, калькулятора, компьютера;
устной прикидки, и оценки результата вычислений, проверки результата вычислений выполнением обратных действий;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
интерпретации графиков реальных зависимостей между величинами.
В результате изучения курса геометрии 7-го класса учащиеся должны уметь:
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать на чертежах и моделях геометрические фигуры (отрезки, углы, треугольники и их частные виды), различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразование фигур;
вычислять значения геометрических величин (длин отрезков, градусную меру углов);
решать геометрические задания, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический аппарат;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве.
использовать приобретенные знания, умения, навыки в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
решения практических задач;
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Общеучебные умения, навыки и способы деятельности.
В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся, оканчивающие основную школу, и достижение которых является обязательным условием положительной аттестации ученика за курс основной школы. Эти требования структурированы по трем компонентам: «знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни». При этом последние два компонента представлены отдельно по каждому из разделов содержания.
ТРЕБОВАНИЯ К УРОВНЮ
ПОДГОТОВКИ ВЫПУСКНИКОВ
В результате изучения математики ученик должен
знать/понимать1
существо понятия математического доказательства; приводить примеры доказательств;
существо понятия алгоритма; приводить примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
Арифметика
уметь
выполнять устно арифметические действия: сложение и вычитание двузначных чисел и десятичных дробей с двумя знаками, умножение однозначных чисел, арифметические операции с обыкновенными дробями с однозначным знаменателем и числителем;
переходить от одной формы записи чисел к другой, представлять десятичную дробь в виде обыкновенной и в простейших случаях обыкновенную в виде десятичной, проценты — в виде дроби и дробь – в виде процентов; записывать большие и малые числа с использованием целых степеней десятки;
выполнять арифметические действия с рациональными числами, сравнивать рациональные и действительные числа; находить в несложных случаях значения степеней с целыми показателями и корней; находить значения числовых выражений;
округлять целые числа и десятичные дроби, находить приближения чисел с недостатком и с избытком, выполнять оценку числовых выражений;
пользоваться основными единицами длины, массы, времени, скорости, площади, объема; выражать более крупные единицы через более мелкие и наоборот;
решать текстовые задачи, включая задачи, связанные с отношением и с пропорциональностью величин, дробями и процентами;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения несложных практических расчетных задач, в том числе c использованием при необходимости справочных материалов, калькулятора, компьютера;
устной прикидки и оценки результата вычислений; проверки результата вычисления, с использованием различных приемов;
интерпретации результатов решения задач с учетом ограничений, связанных с реальными свойствами рассматриваемых процессов и явлений.
Алгебра
уметь
составлять буквенные выражения и формулы по условиям задач; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления, осуществлять подстановку одного выражения в другое; выражать из формул одну переменную через остальные;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним, системы двух линейных уравнений и несложные нелинейные системы;
решать линейные и квадратные неравенства с одной переменной и их системы,
решать текстовые задачи алгебраическим методом, интерпретировать полученный результат, проводить отбор решений, исходя из формулировки задачи;
изображать числа точками на координатной прямой;
определять координаты точки плоскости, строить точки с заданными координатами; изображать множество решений линейного неравенства;
распознавать арифметические и геометрические прогрессии; решать задачи с применением формулы общего члена и суммы нескольких первых членов;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, для составления формул, выражающих зависимости между реальными величинами; для нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследовании построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами, при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Геометрия
уметь
пользоваться геометрическим языком для описания предметов окружающего мира;
распознавать геометрические фигуры, различать их взаимное расположение;
изображать геометрические фигуры; выполнять чертежи по условию задач; осуществлять преобразования фигур;
распознавать на чертежах, моделях и в окружающей обстановке основные пространственные тела, изображать их;
в простейших случаях строить сечения и развертки пространственных тел;
проводить операции над векторами, вычислять длину и координаты вектора, угол между векторами;
вычислять значения геометрических величин (длин, углов, площадей, объемов); в том числе: для углов от 0 до 180° определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них, находить стороны, углы и площади треугольников, длины ломаных, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;
решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними, применяя дополнительные построения, алгебраический и тригонометрический аппарат, соображения симметрии;
проводить доказательные рассуждения при решении задач, используя известные теоремы, обнаруживая возможности для их использования;
решать простейшие планиметрические задачи в пространстве;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания реальных ситуаций на языке геометрии;
расчетов, включающих простейшие тригонометрические формулы;
решения геометрических задач с использованием тригонометрии
решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);
построений геометрическими инструментами (линейка, угольник, циркуль, транспортир).
Элементы логики, комбинаторики,
статистики и теории вероятностей
уметь
проводить несложные доказательства, получать простейшие следствия из известных или ранее полученных утверждений, оценивать логическую правильность рассуждений, использовать примеры для иллюстрации и контрпримеры для опровержения утверждений;
извлекать информацию, представленную в таблицах, на диаграммах, графиках; составлять таблицы, строить диаграммы и графики;
решать комбинаторные задачи путем систематического перебора возможных вариантов и с использованием правила умножения;
вычислять средние значения результатов измерений;
находить частоту события, используя собственные наблюдения и готовые статистические данные;
находить вероятности случайных событий в простейших случаях;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выстраивания аргументации при доказательстве и в диалоге;
распознавания логически некорректных рассуждений;
записи математических утверждений, доказательств;
анализа реальных числовых данных, представленных в виде диаграмм, графиков, таблиц;
решения практических задач в повседневной и профессиональной деятельности с использованием действий с числами, процентов, длин, площадей, объемов, времени, скорости;
решения учебных и практических задач, требующих систематического перебора вариантов;
сравнения шансов наступления случайных событий, для оценки вероятности случайного события в практических ситуациях, сопоставления модели с реальной ситуацией;
понимания статистических утверждений.
ОСНОВНОЕ СОДЕРЖАНИЕ
(Математика 210ч)
Глава 1. Рациональные дроби .
Рациональная дробь. Основное свойство дроби, сокращение дробей. Сложение, вычитание, умножение
и деление дробей. Преобразования рациональных выражений. Функция y=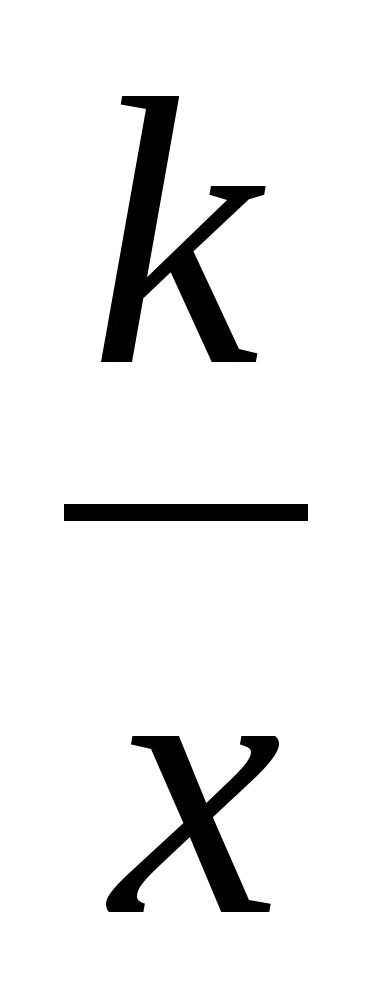 и ее график. и ее график.
Знать:
определение целых, дробных и рациональных выражений;
определение допустимых значений переменных;
определение рациональной дроби;
основное свойство дроби;
определение тождества;
правила сложения и вычитания дробей с одинаковыми знаменателями;
правила сложения и вычитания дробей с разными знаменателями;
правила умножения и деления дробей, возведения дроби в степень;
определение обратной пропорциональности.
Уметь:
находить значения рациональных выражений;
определять целые, дробные и рациональные выражения;
находить допустимые значения переменной;
находить область определения функции;
сокращать дроби;
складывать и вычитать дроби с одинаковыми знаменателями;
складывать и вычитать дроби с разными знаменателями;
умножать и делить дроби, возводить дроби в степень;
преобразовывать рациональные выражения;
строить график функции y= k / x;
строить графики дробно – линейных функций;
представлять дробь в виде суммы дробей.
Глава 2. Четырехугольники
Понятия многоугольника, выпуклого многоугольника. Параллелограмм и его признаки и свойства. Трапеция. Прямоугольник, ромб, квадрат и их свойства. Осевая и центральная симметрии.
Знать:
понятия многоугольника и его элементов, выпуклого многоугольника;
формулу суммы углов выпуклого многоугольника;
понятие четырехугольника и его элементов;
чему равна сумма углов выпуклого четырехугольника;
определение, свойства и признаки параллелограмма;
определение трапеции, виды трапеции, свойства и признаки равнобедренной трапеции;
теорему Фалеса;
определение, свойства и признак прямоугольника;
определение, свойства и признак ромба;
определение и свойства квадрата;
понятия осевой и центральной симметрии.
Уметь:
находить сумму углов выпуклого многоугольника;
решать задачи, применяя свойства и признаки прямоугольника, параллелограмма, ромба, трапеции, квадрата;
строить и распознавать четырехугольники;
строить симметричные фигуры;
Глава 3. Квадратные корни
Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция y = 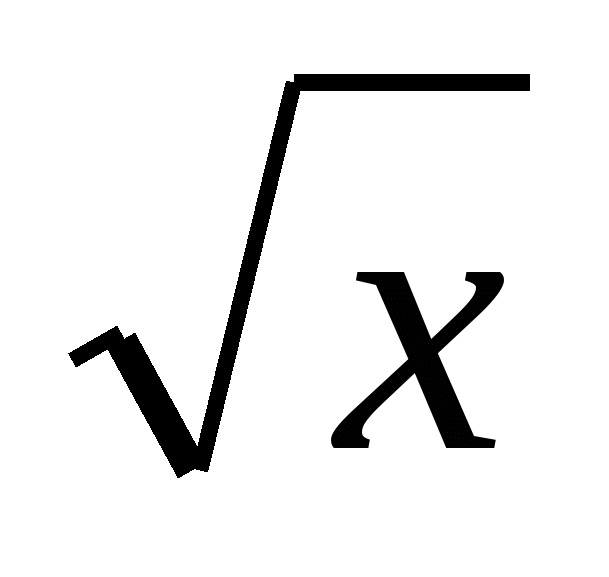 , ее свойства и график. , ее свойства и график.
Знать:
определение натуральных, целых и рациональных чисел;
определение иррациональных и действительных чисел;
определение квадратного и арифметического квадратного корня из числа;
свойства функции y = 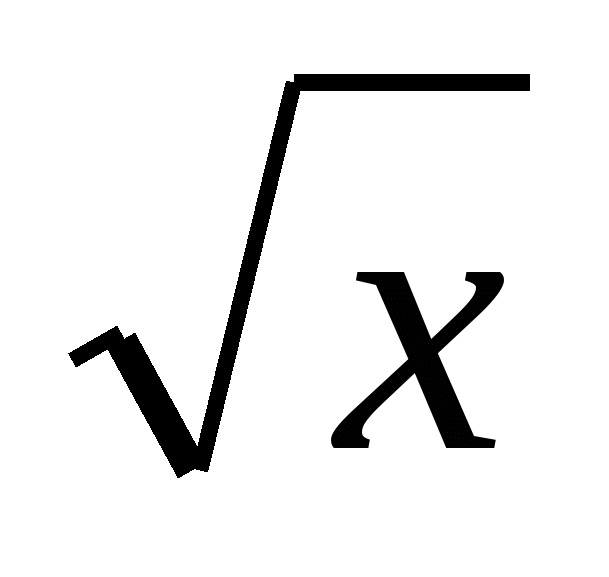 ; ;
правила вычисления квадратного корня из произведения и дроби;
правила вычисления квадратного корня из степени.
Уметь:
сравнивать рациональные числа;
представлять рациональные числа в виде бесконечной десятичной дроби;
сравнивать иррациональные и действительные числа;
вычислять квадратные корни;
решать уравнения вида: x2 = a;
находить приближенное значение квадратного корня;
строить график функции y = 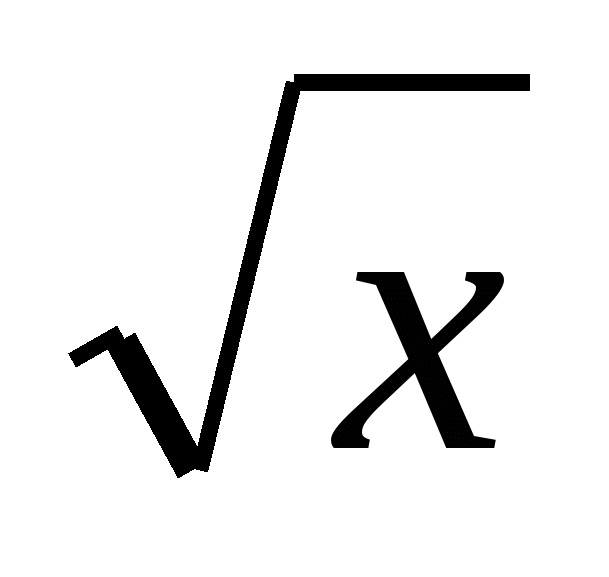 ; ;
вычислять квадратный корень из произведения и дроби;
вычислять квадратный корень из степени;
выносить множитель из-под знака корня;
вносить множитель под знак корня;
преобразовывать выражения, содержащие квадратные корни.
Преобразовывать двойные радикалы
Глава 4. Площади фигур
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
Знать:
понятие площади многоугольника;
единицы измерения площадей;
свойства площадей;
формулу площади квадрата;
теорему и формулу площади прямоугольника;
теорему и формулу площади параллелограмма;
теорему и формулу площади треугольника;
следствия из теоремы о площади треугольника;
теорему об отношении площадей треугольников, имеющих равные углы;
теорему и формулу площади трапеции;
теорему Пифагора и ей обратную.
Уметь:
вычислять площади квадрата, прямоугольника, параллелограмма, ромба, треугольника, трапеции;
применять теорему Пифагора и ей обратную при решении задач.
Глава 5. Квадратные уравнения
Квадратное уравнение. Формулы корней квадратного уравнения. Теорема Виета. Решение рациональных уравнений. Решение задач, приводящих к квадратным и рациональным уравнениям.
Знать:
определение квадратного уравнения;
определение неполного квадратного уравнения;
формулы полных и неполных квадратных уравнений;
определение приведенного квадратного уравнения;
определение дискриминанта квадратного уравнения;
формулу дискриминанта квадратного уравнения;
формулы корней квадратного уравнения;
правило решения квадратного уравнения;
теорему Виета и обратную ей теорему;
определение целых и дробных рациональных уравнений;
правило решения дробных рациональных уравнений.
Уметь:
решать неполные квадратные уравнения;
решать квадратные уравнения выделением квадрата двучлена() также задачи на известные учащимся зависимости между величинами ;
решать квадратные уравнения по формуле;
решать уравнения, сводящиеся к квадратным
решать задачи с помощью квадратных уравнений;
применять теорему Виета и обратную теорему;
раскладывать квадратный трехчлен на множители
Раскладывать многочлена на множители
решать дробные рациональные уравнения;
решать задачи с помощью рациональных уравнений;
решать графически уравнения.
Решать уравнения с параметрами
Глава 6. Подобные треугольники
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника.
Знать:
определение отношения отрезков;
определение подобных треугольников;
теорему об отношении площадей подобных треугольников;
три признака подобия треугольников;
определение средней линии треугольника;
теорему о средней линии треугольника;
свойство медиан треугольника;
определение среднего пропорционального двух отрезков;
свойство высоты и катета прямоугольного треугольника;
определения синуса, косинуса и тангенса острого угла прямоугольного треугольника;
основное тригонометрическое тождество.
Уметь:
применять теорему об отношении площадей подобных треугольников при решении задач;
решать задачи, применяя признаки подобия треугольников;
решать задачи на построение, используя метод подобия;
решать задачи, применяя метод подобия;
решать задачи на среднюю линию треугольника;
решать задачи, применяя соотношения между сторонами и углами прямоугольного треугольника.
Глава 7. Неравенства
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной.
Знать:
определение сравнения чисел;
свойства числовых неравенств;
теоремы о почленном сложении и умножении числовых неравенств;
все виды числовых промежутков;
определение пересечения и объединения множеств
определение решения неравенства;
свойства, используемые при решении неравенств;
определение линейного неравенства с одной переменной;
определение решения системы неравенств с одной переменной.
Уметь:
доказывать неравенства;
применять свойства числовых неравенств;
оценивать значения выражений;
складывать, вычитать, умножать и делить почленно числовые неравенства;
изображать на координатной прямой числовые промежутки;
записывать промежутки, изображенные на рисунке;
решать линейные неравенства с одной переменной;
решать системы неравенств с одной переменной.
Решать простейшие неравенства с модулем
Глава 8. Степень с целым показателем
Степень с целым показателем и ее свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями.
Знать:
определение степени с целым отрицательным показателем;
свойства степени с целым показателем;
определение стандартного вида числа.
Уметь:
вычислять степени с целым отрицательным показателем;
применять свойства степени с целым показателем;
записывать числа в стандартном виде;
выполнять действия с числами, записанными в стандартном виде;
Глава 9. Статистические исследования.
Сбор и группировка статистической информации. Наглядное представление статистической информации (графики, диаграммы, частоты).
Знать:
способы сбора и группировки статистической информации.
Приемы наглядного представления статистической информации (графики, диаграммы, частоты).
Уметь:
Читать статистическую информацию по диаграммам, графикам, гистограммам.
Глава 10. Окружность
Касательная к окружности и ее свойства. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
Знать:
три случая взаимного расположения прямой и окружности;
определение касательной к окружности;
теорему о свойстве касательной к окружности;
свойство отрезков касательных к окружности;
теорему, обратную теореме о свойстве касательной (признак касательной);
определение полуокружности;
определение центрального угла;
как определяется градусная мера дуги окружности;
определение вписанного угла;
теорему о вписанном угле и два следствия;
теорему о произведении отрезков пересекающихся хорд;
теорему о биссектрисе угла и следствие;
определение серединного перпендикуляра к отрезку;
теорему о серединном перпендикуляре к отрезку и следствие;
теорему о пересечении высот треугольника;
четыре замечательные точки;
определение вписанной окружности;
теорему об окружности, вписанной в треугольник;
свойство сторон четырехугольника, в который можно вписать
окружность;
определение описанной окружности;
теорему об окружности, описанной около треугольника;
свойство углов четырехугольника, около которого можно описать окружность;
в какой четырехугольник можно вписать окружность и около какого четырехугольника можно описать окружность.
Уметь:
строить окружность с помощью циркуля;
строить касательную к окружности;
решать задачи на нахождение расстояния от центра окружности до прямой;
решать задачи, применяя теорему о свойстве касательной;
находить градусную меру дуги окружности;
находить градусную меру вписанного угла;
решать задачи, применяя теорему о биссектрисе, серединном перпендикуляре, о высотах треугольника;
строить вписанные и описанные окружности.
Глава11. Функции и графики
Функция, область определения и область значений функции. Растяжение и сжатие графиков. Параллельный перенос графиков функций. Функции у=х-1 и у=х-2.. Дробно – линейная функция и ее график Графики функций, содержащих модуль.
Знать:
понятие область определения, область значений функции.
Уметь:
выполнять преобразования графиков функций;
строить графики дробно – линейных функций и функций, содержащих модуль.
Повторение.
Цель: повторение и систематизация полученных в течение учебного года знаний.
Знать:
Математические термины и формулы;
Различные методы решения задач, уравнений и неравенств, систем уравнений и неравенств;
Графики основных элементарных функций и их свойства;
Преобразования выражений.
Уметь:
Правильно употреблять математические термины и формулы;
Применять различные методы при решении задач, уравнений и неравенств, систем уравнений и неравенств;
Выполнять преобразования различных выражений;
Выполнять действия с числами, корнями, степенями, многочленами, алгебраическими дробями, приближенными значениями;
Осуществлять в выражениях и формулах числовые подстановки, выполнять соответствующие вычисления;
Выражать из формул одни переменные через другие;
Строить графики основных элементарных функций; опираясь на графики, описывать свойства этих функций.
|
|
|
 Скачать 1.11 Mb.
Скачать 1.11 Mb.