Графики и модуль
 Скачать 27.05 Kb. Скачать 27.05 Kb.
|
  МЕТОДИЧЕСКАЯ РАЗРАБОТКА УЧИТЕЛЬ МАТЕМАТИКИ КАЗАНЦЕВА Т.А. ГИМНАЗИЯ №13 г. ТОМСК Занятие элективного курса по теме: Графики и модуль. Цель занятия: повторить приёмы построения графиков элементарных функций и научить учащихся строить графики, содержащие модуль. Ход занятия:
 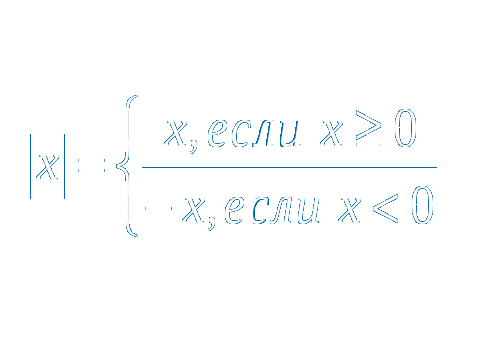 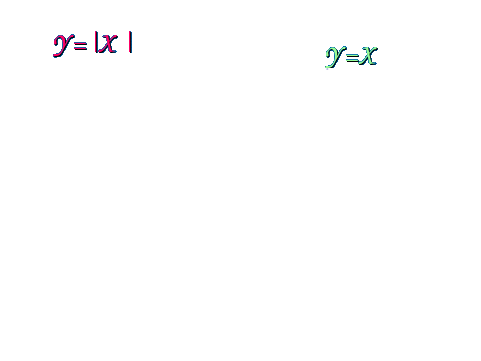
у =
Рассмотрим примеры построения графиков функций с использованием слайдов компьютерной презентации. Пример 1. Построение: 1. Строим график функции у = х-3. 2. График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ. 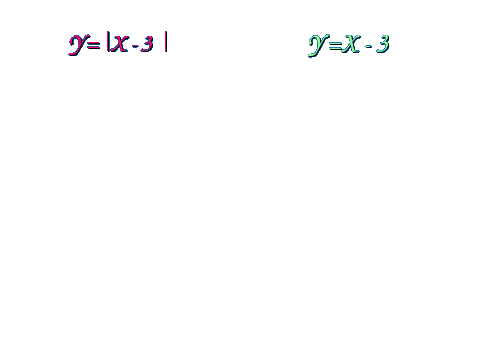 Пример 2. Построение: 1. Строим график функции у = х2-2. 2. График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ. 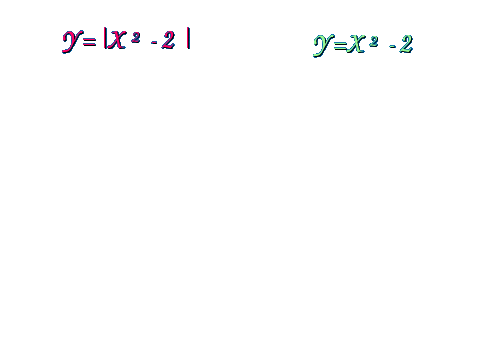 Пример 3. Построение: 1. Строим график функции у = - (х + 3)2 +2 2. График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ. 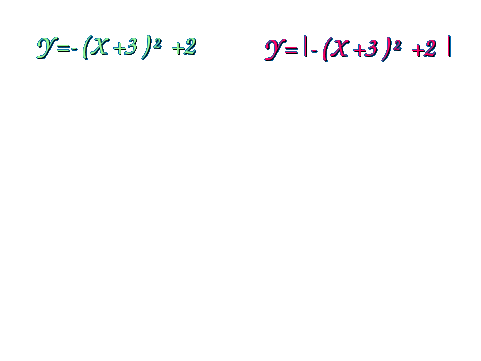 Пример 4. Построение: 1. Строим график функции у = х2 - 5х + 6 2. График нижней полуплоскости отображаем вверх симметрично относительно оси ОХ. 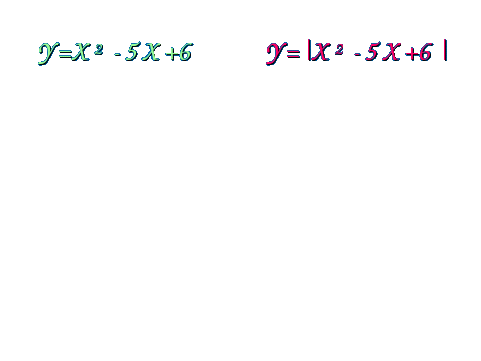 Пример 5. Построение: 1 способ. у = 3 |х| -6 2 способ. Строим график функции у = 3х-6 для х >0. Достраиваем его левую часть для х < 0, симметрично построенной относительно оси ОУ. 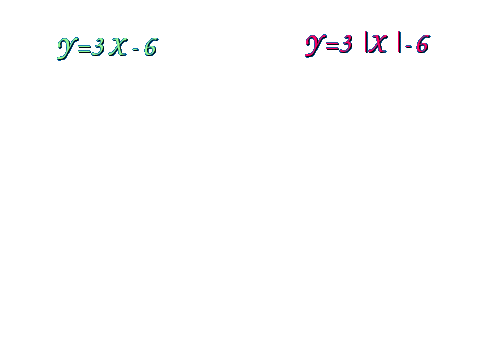 Пример 6. Построение: При х 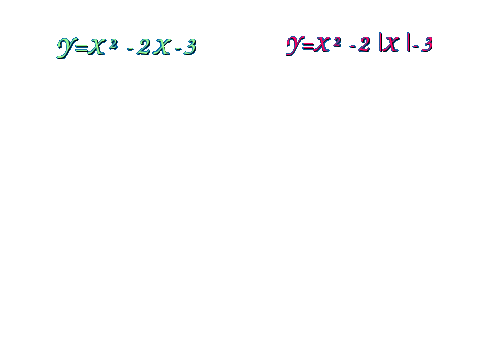 Пример 7. Построение: 1. Строим график функции у = х - 2. 2. Строим график функции у = |х - 2|. 3. Строим график функции у = |х - 2| - 2. 4. Строим график функции у = ||х - 2| - 2| 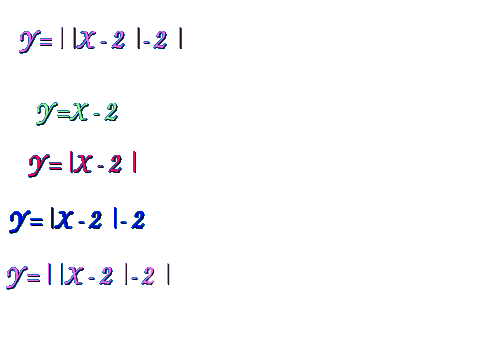 Пример 8. Построение: 1. Строим график функции у = х2 - 5 |х| + 6. 2. Строим график функции у = |х2 - 5 |х| + 6| 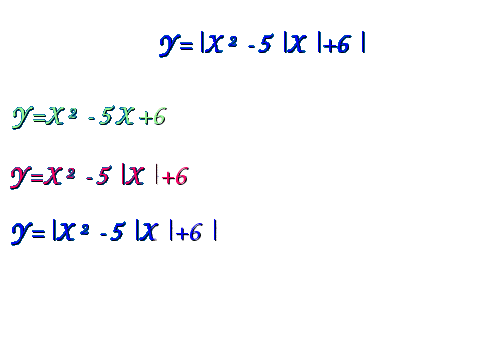 III. Самостоятельная работа по группам (задание из сборника ЕГЭ 9 класс). Постройте графики функций: I группа: № 4.31(1), у = II группа: № 4.31 (2), у = III группа: № 4.32 (1), у = х IV группа: № 4.32 (2), у = - х IV. Подведение итогов занятия, защита групповых работ. |