Метод математической индукции как эффективный метод доказательства гипотез

Название	Метод математической индукции как эффективный метод доказательства гипотез
	Прошина Н.В
Дата	27.02.2016
Размер	133.52 Kb.
Тип	Исследовательская работа

Муниципальное бюджетное общеобразовательное учреждение

средняя общеобразовательная школа №15 города Кузнецка

Исследовательская работа по математике

на тему:

« Метод математической индукции как

эффективный метод доказательства гипотез»
Автор работы:

Ученица 10 «А»класса

Колтунова Валерия

Руководитель:

учитель математики

Прошина Н.В.

2012г.

Содержание

Введение…………………………………………………………………………..3

Обзор литературы……………………………………………………………….5

Основные результаты исследования……………………………………………6

1) Общие и частные утверждения …………………………………………….6

2) Дедукция………………………………………………………………….6

3) Индукция……………………………………………………………………….6

4) Неполная индукция……………………………………………………………6

5) Полная индукция……………………………………………………………....7

6) Метод математической индукции……………………………………………7

7) Применение метода математической индукции…………..………………..8

8) Второй вариант метода математической индукции………………………10 9)Замечание к методу математической индукции……………………11 Заключение………………………………………………………………………12Список литературы……………………………………………………………..14

Введение

Актуальность темы

Одной из отличительных черт математики является дедуктивное построение теории. Но дедукция не является единственным методом научного мышления. В экспериментальных науках велика роль индуктивных выводов. В математике индукция часто позволяет угадать формулировку теорем, а в ряде случаев и наметить пути доказательств.

Для исследования я выбрал тему « Метод математической индукции», т. к. в школьной программе с методом математической индукции знакомятся только поверхностно. В то время как подробное знакомство с этим методом полезно учащимся не только из-за расширения их кругозора, но также и потому, что на его принципе основано решение многих задач (включая олимпиадные). Мною был изучен принцип математической индукции, а также его широкое применение в решении задач на суммирование, доказательстве тождеств, доказательстве и решении неравенств (в частности неравенства Бернулли), решении вопроса делимости, при изучении свойств числовых последовательностей, при решении геометрических задач.
Цель работы: познакомиться с методом математической индукции, систематизировать знания по данной теме и применить её при решении математических задач и доказательстве теорем, обосновать и наглядно показать практическое значение метода математической индукции как необходимого фактора для решения задач.
Задачи работы:

1. Проанализировать литературу по данной теме.

2. Освоить разные методы и методики работы.

3.Обобщить и систематизировать знания по данной теме.

4. Совершенствовать знания, умения, навыки по данной теме.

5. Развивать творческий подход к решению задач.

6.Прорешать задачи различных видов, применяя данный метод.

7.Предоставить выводы по данной теме.
Гипотеза

Метод математической индукции приводит только к верным выводам.
Методы и методики исследования, используемые в работе

1.Анализ математической литературы и ресурсов Интернета по данной теме.

2.Репродуктивное воспроизведение изученного материала.

3.Познавательно- поисковая деятельность.

4.Анализ и сравнение данных в поиске решения задач.

5.Постановка гипотез и их поверка.

6.Сравнение и обобщение математических фактов.

7.Решение задач различных видов.

8.Анализ полученных результатов.

Обзор литературы

Метод математической индукции рассматривается во многих учебных пособиях, в методической литературе. Данной теме посвящена книга Соминского И.С. « Метод математической индукции». Кроме теоретического материала в ней даны рекомендации к решению задач. Очень подробно изложен данный метод « Избранные вопросы математики» (составители Боковнев О. А., Фирсов В.В., Шварцбург С. И.). В учебном пособии «Углубленное изучение курса алгебры и математического анализа» Галицкого М. Л. И др. содержатся методические рекомендации по изучению теоретических вопросов, к решению задач по данной теме. Даны дополнительные упражнения для самостоятельного решения. Книга « Задачи повышенной трудности по алгебре и началам анализа» Ивлева Б. М. и др. содержит более сложные задачи по данной теме. В книге Коровина П. П.

« Неравенства» показано применение метода математической индукции при решении неравенств. Более сжато тема рассмотрена в книгах Петракова И. С. «Математические кружки», Виленкина Н. Я. И др. « За страницами учебника математики». В пособии Шарыгина И. Ф. « Факультативный курс по математике» немало трудных задач, снабжённых лишь краткими указаниями.

Основные результаты исследования.

1) В процессе работы я выяснил, что все утверждения можно разделить на общие и частные. Примером общего утверждения является, например, утверждение: «В любом треугольнике сумма двух сторон больше третьей стороны». Частным является, например, утверждение: «Число 136 делится на 2».

2) Переход от общих утверждений к частным называется дедукцией. В математике дедуктивный метод мы применяем, например, в рассуждениях такого типа: данная фигура - прямоугольник; у каждого прямоугольника диагонали равны, следовательно, и у данного прямоугольника диагонали равны.

3) Но наряду с этим математике часто приходится от частных утверждений переходить к общим, т.е. использовать метод, противоположный дедуктивному, который называется индукцией.

Индуктивный подход обычно начинается с анализа и сравнения, данных наблюдения или эксперимента. Многократность повторения какого-либо факта приводит к индуктивному обобщению. Результат, полученный индукцией, вообще говоря, не является логически обоснованным, доказанным. Известно много случаев, когда утверждения, полученные индукцией, были неверными. Т. е. индукция может привести как к верным, так и к неверным выводам.

4) Рассмотрим пример. Подставляя в квадратный трехчлен P(х)= х²+ х+ 41 вместо х натуральные числа 1,2,3,4,5, найдем: Р(1)= 43; Р(2)=47; Р(3)= 53; Р(4)= 61; Р(5)= 71. Все значения данного трехчлена являются простыми числами. Подставляя вместо х числа 0, -1, -2, -3, -4, получим: Р(0)=41;

Р(-1)=41; Р(-2)=43; Р(-3)=47; Р(-4) =53. Значения данного трехчлена при указанных значениях переменной х также являются простыми числами. Возникает гипотеза, что значение трехчлена Р(х) является простым числом при любом целом значении х. Но высказанная гипотеза ошибочна, так как, например, Р(41)= 41²+41+41=41∙43.

Так как при этом методе вывод делается после разбора нескольких примеров, не охватывающих всех возможных случаев, то этот метод называется неполной или несовершенной индукцией.

Метод неполной индукции, как мы видим, не приводит к вполне надежным выводам, но он полезен тем, что позволяет сформулировать гипотезу, которую потом можно доказать точным математическим рассуждением или опровергнуть. Иными словами, неполная индукция в математике не считается законным методом строгого доказательства, но является мощным эвристическим методом открытия новых истин.

5) Если же вывод делается на основании разбора всех случаев, то такой метод рассуждений называют полной индукцией.

Вот пример подобного рассуждения. Пусть требуется установить, что каждое натуральное чётное число п в пределах 10< п < 20 представимо в виде суммы двух простых чисел. Для этого возьмём все такие числа и выпишем соответствующие разложения: 10=7+3; 12=7+5; 14=7+7; 16=11+5; 18=13+5; 20=13+7. Эти шесть равенств показывают, что каждое из интересующих нас чисел действительно представляется в виде суммы двух простых слагаемых.

6) Пусть некоторое утверждение справедливо в нескольких частных случаях. Рассмотрение всех остальных случаев или совсем невозможно, или требует большого числа вычислений. Как же узнать, справедливо ли это утверждение вообще? Этот вопрос иногда удается решить посредством применения особого метода рассуждений, называемого методом математической индукции. В основе данного метода лежит принцип математической индукции.

Если предложение, зависящее от натурального числа n, истинно для n=1 и из того, что оно истинно для n=k (где k-любое натуральное число), следует, что оно истинно и для следующего числа n=k+1, то предположение истинно для любого натурального числа n.

Метод математической индукции - есть эффективный метод доказательства гипотез (утверждений), основанный на использовании принципа математической индукции, поэтому он приводит только к верным выводам.

Методом математической индукции можно решать не все задачи, а только задачи, параметризованные некоторой переменной. Эта переменная называется переменной индукции.

7) Метод математической индукции имеет наибольшее применение в арифметике, алгебре и теории чисел.

Пример 1. Найти сумму Sп =

Сначала найдем суммы одного, двух и трех слагаемых. Имеем:

S₁ = ; S₂ = ; S₃= .

В каждом из этих случаев получается дробь, в числителе которой стоит число слагаемых, а в знаменателе — число, на единицу большее числа слагаемых. Это позволяет высказывать гипотезу ( предположение), что при любом натуральном п Sп = .

Для проверки этой гипотезы воспользуемся методом математической индукции.

1) При п = 1 гипотеза верна, так как S₁ =

.

2) Предположим, что гипотеза верна при п = k, то есть

S_k =

.

Докажем, что тогда гипотеза должна быть верной и при п = k+1, то есть

S_k₊₁ =

.

Действительно, S _k₊₁ = S_k

S _k₊₁ =

Таким образом, исходя из предположения, что гипотеза S_п=

верна при п = k, мы доказали, что она верна и при п = k + 1.

Поэтому формула S_п= верна при любом натуральном п.

Пример 2. Доказать, что для любого натурального числа п и любого действительного числа а > -1 имеет место неравенство, называемое неравенством Бернулли ( названо в честь швейцарского математика XVII в. Якова Бернулли): (1+a) ^п≥ 1 + ап.

1) Если п=1, то очевидно, что неравенство верно: (1+а)¹ ≥ 1+а.

2) Предположим, что неравенство верно при n=k: (1+a)^k≥ 1 + ak.

Умножим обе части последнего неравенства на положительное число 1+ а, в результате чего получим (1+a)^k⁺¹ ≥ 1+ak+a+a²k.

Отбрасывая последнее слагаемое в правой части неравенства, мы уменьшаем правую часть этого неравенства, а поэтому (1+a)^k⁺¹ ≥ a(k+1).

Полученный результат показывает, что неравенство верно и при n=k+1.

Обе части доказательства методом математической индукции проведены, и, следовательно, неравенство справедливо при любом натуральном п.

Заметим, что всё решение было разбито на четыре этапа: база ( показываем, что доказываемое утверждение верно для некоторых простейших частных случаев ( п = 1); предположение (предполагаем, что утверждение доказано для первых к случаев; шаг ( в этом предположении доказываем утверждение для случая п = к + 1); вывод ( утверждение верно для всех случаев, то есть для всех п).

8) Второй вариант метода математической индукции.

Некоторые утверждения справедливы не для всех натуральных п, а лишь для натуральных п, начиная с некоторого числа р. Такие утверждения иногда удается доказать методом, несколько отличным от того, который описан выше, но вполне аналогичным ему. Состоит он в следующем.

Утверждение верно при всех натуральных значениях п ≥ р, если: 1)оно верно при п =р (а не при п = 1, как было сказано выше); 2)из справедливости этого утверждения при п = k_,где k ≥ р (а не k ≥ 1, как сказано выше), вытекает, что оно верно и при п = k + 1.

Пример 1. Докажите, что для любого

справедливо равенство

Обозначим произведение в левой части равенства через

, т.е.

мы должны доказать, что

.

Для n=1 формула не верна ( 1- 1) = 1( неверно ).

1) Проверим, что эта формула верна для n = 2.

- верно.

2) Пусть формула верна для n = k, т.е.

3) Докажем, что это тождество верно и для n = k + 1, т.е.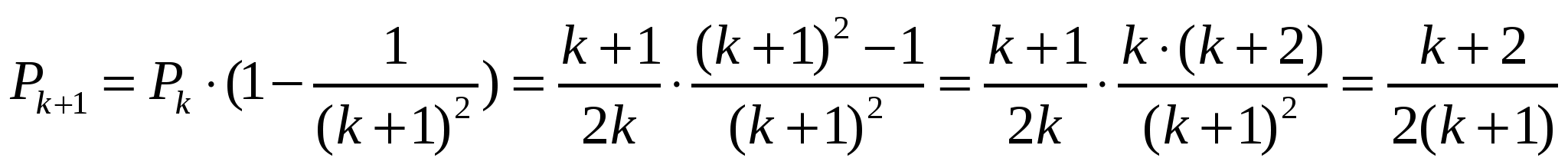

По принципу математической индукции равенство справедливо для любого натурального

.

Пример 2. Докажите, что 2

>2n + 1 при любом натуральном n

3.

1) При n = 3 неравенство верно. 2

3 + 1.

2) Предположим, что 2

>2k + 1 (k

3).

3) Докажем, что 2

> 2(k + 1) + 1.

В самом деле, 2

= 2

>2(2k + 1) =(2k + 3)(2k - 1) > 2k + 3, так как 2k – 1>0 при любом натуральном значении k. Следовательно, 2

>2n + 1 при всех n

3.

9) Замечание к методу математической индукции.

Доказательство методом математической индукции состоит из двух этапов.

l-й этап. Проверяем, верно ли утверждение при п = 1 (или при п = р, если речь идет о методе, описанном выше).

2-й э т а п. Допускаем, что утверждение верно при п = k, и, исходя из этого, доказываем, что оно верно и при п = k+1.

Каждый из этих этапов по-своему важен, рассматривая пример P(х)= х²+ х+41, мы убедились, что утверждение может быть верным в целом ряде частных случаев, но неверным вообще. Этот пример убеждает нас в том, насколько важен 2-й этап доказательства методом математической индукции. Опустив его, можно прийти к неверному выводу.

Не следует, однако, думать, что 1-й этап менее важен, чем 2-й. Сейчас я приведу пример, показывающий, к какому нелепому выводу можно прийти, если опустить 1-й этап доказательства.

«Теорем а». При любом натуральном п число 2п +1 четное.

Доказательство. Пусть эта теорема верна при п = k,то есть число 2k + 1 четное. Докажем, что тогда число 2(k+1)+1 также четно.

Действительно, 2(k+1)+1 = (2k+1)+2.

По предположению число 2k +1 четно, а поэтому его сумма с четным числом 2 также четна. Теорема «доказана».

Если бы мы не забыли проверить, верна ли наша «теорема» при п = 1, мы не пришли бы к такому «результату».

Заключение

Итак, индукция (от лат. inductio — наведение, побуждение) — одна из форм умозаключения, приём исследования, применяя который от знания отдельных фактов приходят к общим положениям. Индукция бывает полная и неполная. Метод неполной индукции состоит в переходе к универсальной формулировке после проверки истинности частных формулировок для отдельных, но не всех значений n. Применяя полную индукцию, мы лишь тогда считаем себя вправе объявить об истинности универсальной формулировки, когда убедились в её истинности для каждого без исключения значения n. Метод математической индукции – метод доказательства, основанный на принципе математической индукции. Он позволяет в поисках общего закона испытывать гипотезы, отбрасывать ложные и утверждать истинные.

Метод математической индукции является одной из теоретических основ при решении задач на суммирование, доказательстве тождеств, доказательстве и решении неравенств, решении вопроса делимости, при изучении свойств числовых последовательностей, при решении геометрических задач и т. д.

Знакомясь с методом математической индукции, я изучала специальную литературу, консультировалась с педагогом, анализировала данные и решения задач, пользовалась ресурсами Интернета, выполняла необходимые вычисления.

Вывод:

В ходе работы я узнала, чтобы решать задачи методом математической индукции нужно знать и понимать основной принцип математической индукции.

Достоинством метода математической индукции является его универсальность, так как с помощью этого метода можно решить многие задачи. Недостатком неполной индукции является то, что порой она приводит к ошибочным выводам.

Обобщив и систематизировав знания по математической индукции, убедилась в необходимости знаний по теме «метод математической индукции». Кроме того эти знания повышают интерес к математике, как к науке.

Так же в ходе работы приобрела навыки решения задач по использованию метода математической индукции. Считаю, что эти навыки помогут мне в будущем.

Список литературы.

1.Боковнев О. А., Фирсов В. В., Шварцбурд С. И. Избранные вопросы математики. 9 класс. Факультативный курс.-М.: Просвещение, 1979г.

2.Виленкин Н. Я., Шибасов Л. П., Шибасова З. Ф. За страницами учебника математики. Москва: Просвещение, 1996г.

3.Галицкий М. Л., Мошкович М. М., Шварцбурд С. И. Углубленное изучение курса алгебры и математического анализа: методические рекомендации, дидактические материалы.

4.Ивлев Б.М., Абрамов А.М., Дудницин Ю.П., Шварцбурд С.И. М.: Просвещение, 1990г.

5.Коровин П. П. Неравенства. Популярные лекции по математике, выпуск 5-М.: Наука, 1983г.

6.Соминский И.С. Метод математической индукции. Популярные лекции по математике, выпуск 3-М.: Наука, 1974г.

7.Петраков И. С. Математические кружки в 8-10 классах: Кн. для учителя М.: Просвещение, 1987г.

8.Шарыгин И. Ф. Факультативный курс по математике. Решение задач учебное пособие для 10 класса средней школы – М.: Просвещение,1989г.