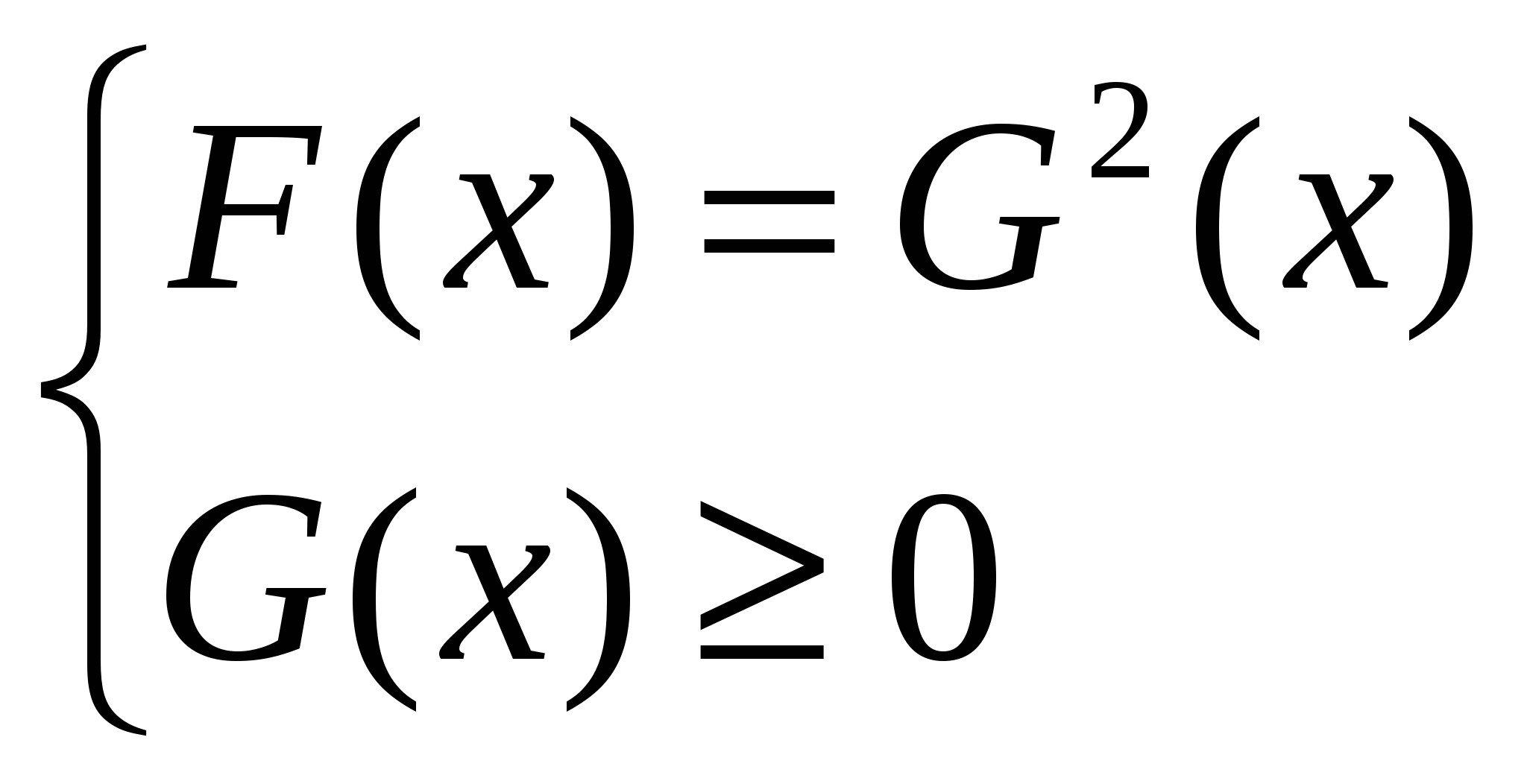Конспект урока алгебры в 11 м классе по теме «Способы решения иррациональных уравнений» Цели
 Скачать 43.47 Kb. Скачать 43.47 Kb.
|
| План – конспект урока алгебры в 11 М классе по теме «Способы решения иррациональных уравнений» Цели:
Тип урока – урок изучения нового материала. ПЛАН УРОКА:
ХОД УРОКА I. Организационный момент Подготовка учащихся к работе на уроке. II. Подготовка к изучению нового материала
а) Определение иррационального уравнения б) Решение уравнений
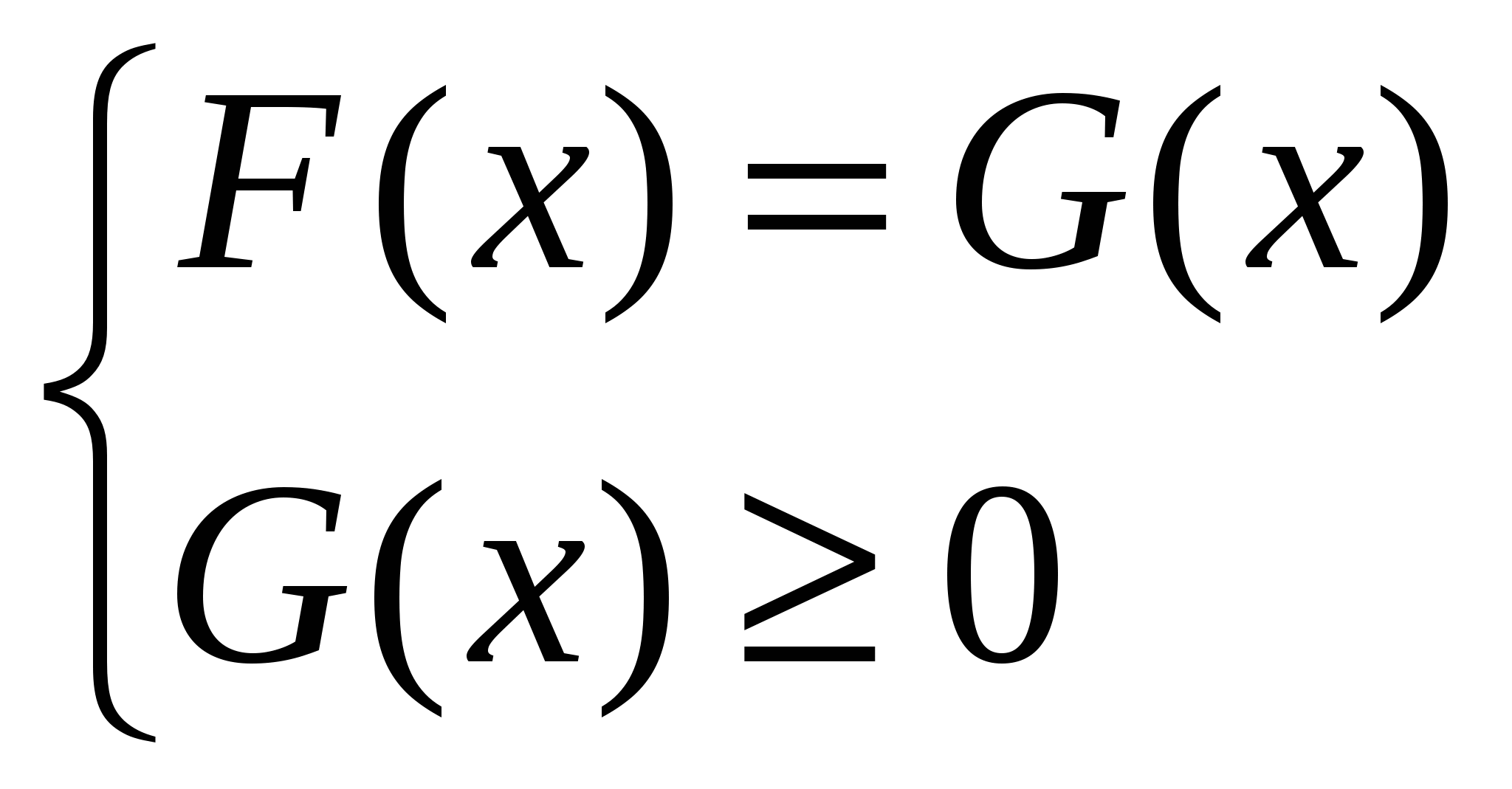 или или 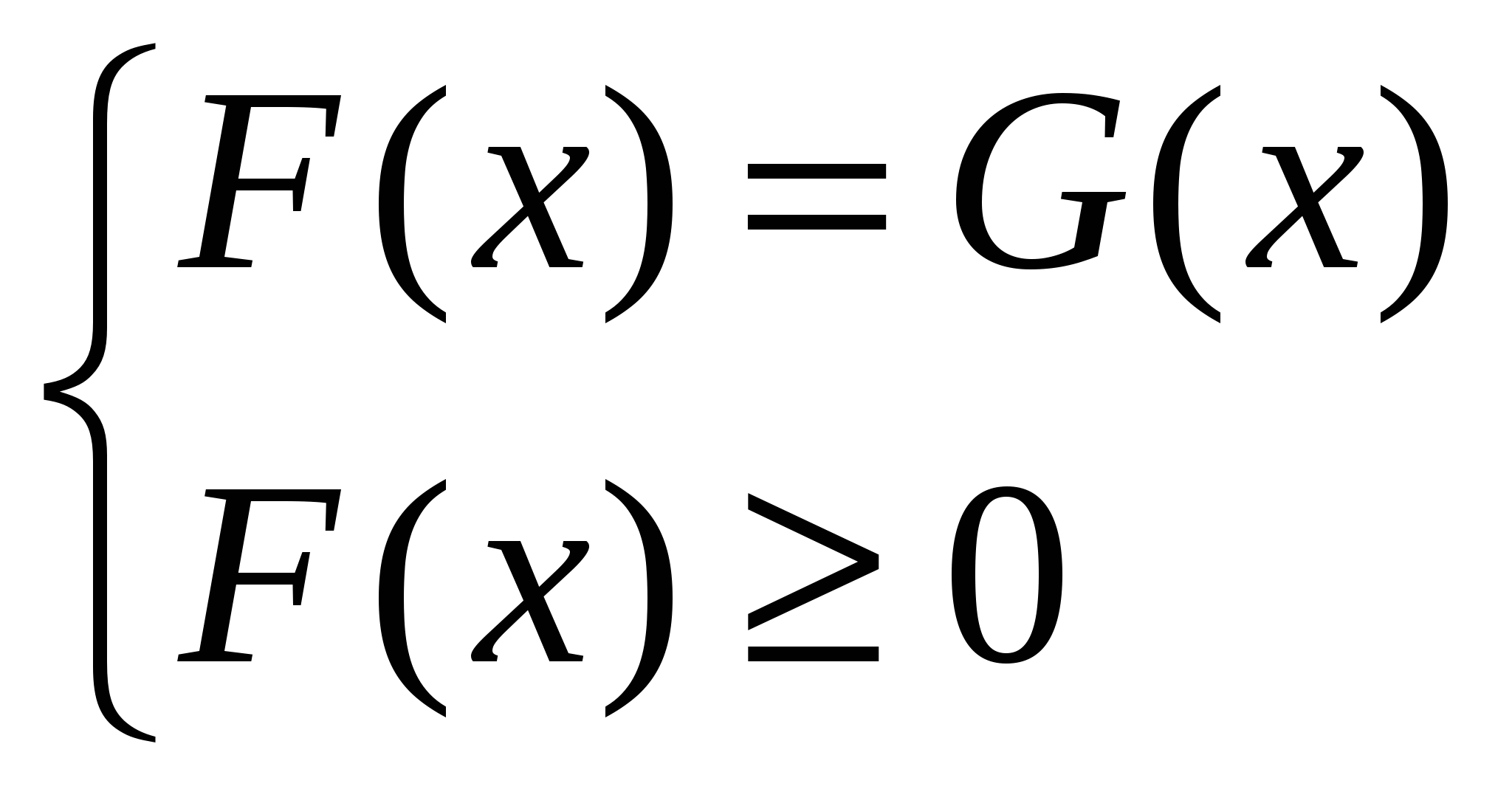 в) Наиболее распространенный метод решения иррациональных уравнений – последовательное возведение в степень. 3. Решите уравнение (Учащиеся должны высказать разные предположения, и они затрудняются решить данное уравнение, учитель предлагает оставить его и решить после изучения других способов решения иррациональных уравнений) III. Изучение нового материала Одним из сложных разделов алгебры, изучаемых в школьной программе, являются иррациональные уравнения, так как отсутствуют общие алгоритмы их решения и приходится делать преобразования, приводящие к уравнениям, не равносильным данным. Рассмотрим случаи, когда проще свести решение уравнения к решению следствия и проверке. Следствия могут быть получены:
1. Пусть дано уравнение Возведем обе части уравнения в куб, воспользовавшись формулой (a + b)3= a3 + b3 + 3ab(a + b). Получим уравнение Заменим сумму кубических корней величиной с и получим следствие последнего уравнения: Пример: Решите уравнение Это уравнение равносильно уравнению Следствием его является уравнение Решение - х = 80. Проверка показывает, что это число является корнем данного уравнения. 2. Некоторые уравнения удобно заменить системой уравнений. Пример: Решите уравнение Возведение в степень не дает результата. Тогда сделаем замену: Заменим данное уравнение системой 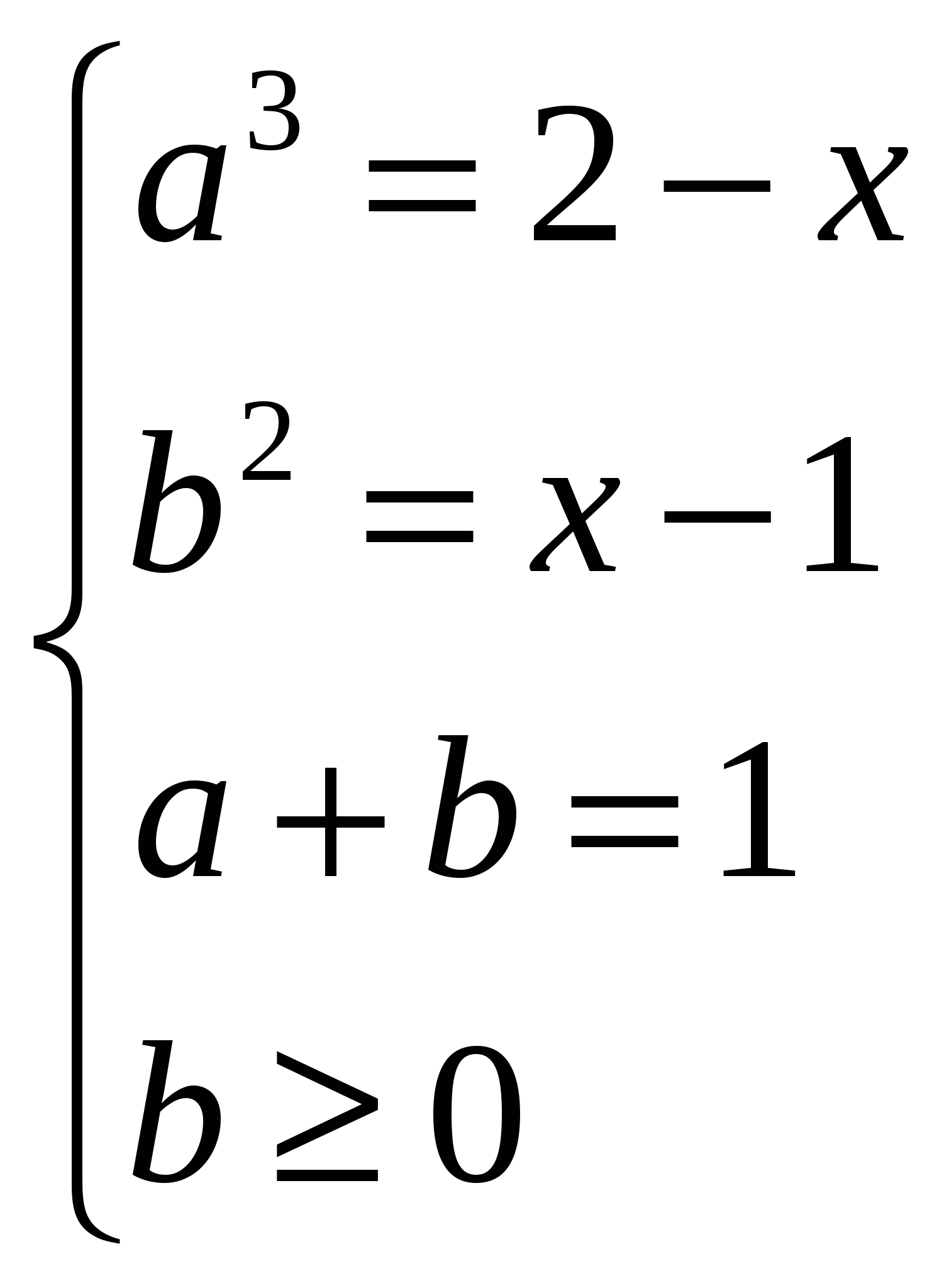 Исключая из первых двух уравнений переменную х, получим систему Исключая из первых двух уравнений переменную х, получим систему 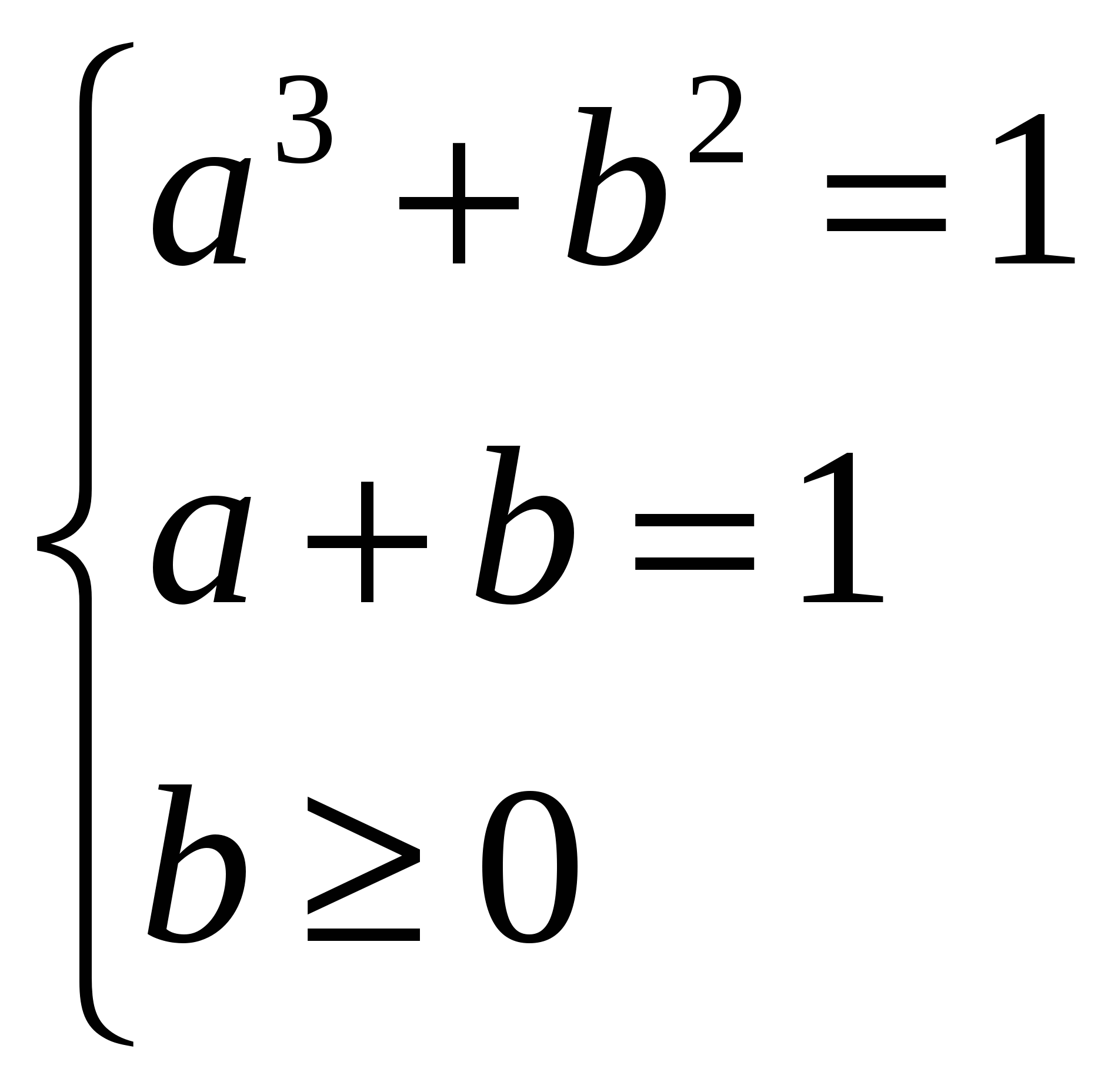 Решаем эту систему методом подстановки, получим a1=0, a2= -2, a3= 1, тогда х1=2, х2=10, х3= 12. Проверка показывает, что все найденные значения х есть корни данного уравнения. Решаем эту систему методом подстановки, получим a1=0, a2= -2, a3= 1, тогда х1=2, х2=10, х3= 12. Проверка показывает, что все найденные значения х есть корни данного уравнения.Этот прием хорош в том случае, когда сумма или разность подкоренных выражений есть константа. 3. Уравнения вида Пример: Решите уравнение Умножив обе части уравнения на разность корней, получим уравнение Сложив почленно эти уравнения, получим 4. При решении некоторых уравнений полезно воспользоваться тем, что функция Пример: Решите уравнение В левой части уравнения сумма возрастающих функций, а в правой — константа, значит уравнение имеет не более одного корня. х = 1 — корень уравнения. 5. Решить уравнение Решение: Обозначая Откуда t = –3, t = 2. Следовательно, Согласно проверке, x = 2 корень исходного уравнения. IV. Первичная проверка понимания 1. Почему данные уравнения не имеют корней? a) б) в) г) 2. Решите уравнения: а) б) в) V. Подведение итогов урока VI. Домашнее задание на выбор: 1. Решить уравнения: 2. Пообобрать или придумать иррациональные уравнения, решаемые изученными приемами 3. Индивидуальное задание для желающих: Найти в пособиях по математике другие способы решения иррациональных уравнений. |