|
Программа по алгебре и началам анализа 10 класс (базовый уровень) Пояснительная записка
Рабочая программа
по алгебре и началам анализа
10 класс
(базовый уровень)
Пояснительная записка
Рабочая программа разработана в соответствии с Примерной программой среднего (полного) образования по математике, с учетом требований федерального компонента государственного стандарта общего образования и основана на программе общеобразовательных учреждений. М., Просвещение, 2009год, Алгебра и начала математического анализа 10-11 классы, авт. Бурмистрова Т.А.
С учетом возрастных особенностей каждого класса выстроена система учебных занятий, спроектированы цели, задачи, продуманы возможные формы контроля, сформулированы ожидаемые результаты обучения.
Рабочая программа ориентирована на использование учебно-методического комплекта:
Колягин Ю.М. Алгебра и начала математического анализа. 10 класс: учебник для общеобразовательных учреждений: базовый и профильный уровни / Ю.М. Колягин и др.; под ред. А.В.Жижченко.-4-е изд.- М.: Просвещение, 2011.
Федорова Н.Е. Изучение алгебры и начала математического анализа в 10 классе : книга для учителя / Н.Е. Федорова, М.В. Ткачева. – М. :Просвещение, 2009.
Шабунин М.И. . Алгебра и начала математического анализа. 10 класс: дидактический материал. Базовый уровень/ М.И. Шабунин и др. – М. : Просвещение,2009.
Ткачева М.В. . Алгебра и начала математического анализа. 10 класс: тематические тесты. ЕГЭ. Базовый и профильный уровни / М.В. Ткачева, Н.Е. Федорова. – М. : Просвещение, 2009
А также дополнительных пособий для подготовки к ЕГЭ:
Жафяров А.Ж. Математика. ЕГЭ-2010. Экспресс-консультация. /А.Ж. Жафяров: Сиб. Унив. Изд-во. 2010.
Математика. Подготовка к ЕГЭ-2013: учебно-тренировочные тесты/ под ред. Ф.Ф. Лысенко.- Ростов н/Д : Легион, 2013.
Д.Э. Шноль Математика. ЕГЭ 2013. Рабочие тетради. ЗадачиВ1,Арифметические задачи / под ред. А.Л. Семёновой и И.В. Ященко.
Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
М.А. Посицельская, С.Е. Посицельская ЕГЭ 2013. Рабочие тетради. ЗадачиВ2, Графики и диаграммы / под ред. А.Л. Семёновой и И.В. Ященко. Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
И.Р. Высоцкий ЕГЭ 2013. Рабочие тетради. Задачи В4, Задачи на наилучший выбор / под ред. А.Л. Семёновой и И.В. Ященко.
Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
С.А .Шестаков ЕГЭ 2013. Рабочие тетради. ЗадачиВ5, Простейшие уравнения / под ред. А.Л. Семёновой и И.В. Ященко.
Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
С.А. Шестаков ЕГЭ 2013. Рабочие тетради. ЗадачиВ7, Значения выражений/ под ред. А.Л. Семёновой и И.В. Ященко.
Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
Д.Д. Гущин, А.В. Малышев ЕГЭ 2013. Рабочие тетради. ЗадачиВ12, Задачи прикладного содержания/ под ред. А.Л. Семёновой и И.В. Ященко. Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
С.А. Шестаков, Д.Д. Гущин ЕГЭ 2013. Рабочие тетради. ЗадачиВ13, Задачи на составление уравнений/ под ред. А.Л. Семёновой и И.В. Ященко. Разработано МИОО. Издание соответствует новому Федеральному государственному общеобразовательному стандарту (ФГОС). Москва. Издательство МЦНМО. 2013.
Интернет – ресурсы:
https://alleng.ru/edu/math3.htm-Типовые (тематические)задания ЕГЭ.
https://eek.diary.ru/p62222263.htm- Подготовка к ЕГЭ по математике.
https://4ege.ru/matematika/page/2- УГЭ портал «Математика».
https://ctege.org/content/view/910/39 - Учебные пособия, разработанные специалистами ФИПИ.
https:// Mathege.ru:8080/or/ege/Main?view=TrainArcyive – Открытый банк заданий ЕГЭ по математике.
Согласно Федеральному базисному учебному плану данная рабочая программа предусматривает следующий вариант организации процесса обучения в 10 классе:
I вариант (базовый уровень) предполагает обучение в объеме 85 часов, 2,5 часа в неделю (2 часа в неделю в 1-м полугодии, 3 часа в неделю во 2 –м полугодии).
Математическое образование в основной школе складывается из следующих содержательных компонентов: арифметика; алгебра; геометрия; элементы комбинаторики; теории вероятности, статистики и логики. В своей совокупности они отражают богатый опыт обучения математики в нашей стане, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты развивались на протяжении всех лет обучения, они естественным образом переплетаются и взаимодействуют в учебных курсах.
В ходе освоения содержания курса учащиеся получают возможность:
развить представление о числах и роли вычислений в человеческой практике; сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру; пространственные представления и изобразительные умения, освоить основные факты и методы планиметрии, познакомиться с простейшими пространственными телами и их свойствами; логическое мышление и речь – умение логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства;
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
изучить свойства и графики элементарных функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
получить представление о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях вывода и прогнозов, носящих вероятностный характер;
сформировать представления об изучаемых понятиях и методах как важнейших средствах математического моделирования реальных процессов и явлений.
Цели обучения математике:
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии;
В ходе преподавания математики в основной школе следует обратить внимание на овладение умениями общеучебного характера, разнообразными способами деятельности, приобретение опыта:
планирования и осуществления алгоритмической деятельности, выполнения заданных и конструирования новых алгоритмов;
решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска путей и способов решения;
исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;
ясного, точного, грамотного изложения своих мыслей в устной и письменной формах, использования различных языков математики (словестного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;
проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;
поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.
С учетом уровней специфики класса выстроена система учебных занятий, спроектированы цели, задачи, планируемые результаты обучения, что представлено в схематической форме ниже. Основой целеполагания является обновление требований к уровню подготовки школьников в системе естественно-математического образования, отражающее важнейшую особенность педагогической концепции Государственного стандарта – переход от суммы «предметных результатов» к «межпредметным результатам».
Реализация календарно-тематического плана обеспечивает освоение общеучебных умений и компетенций в рамках информационно-коммуникативной деятельности:
создание условия для умения логически обосновывать суждения, выдвигать гипотезы и понимать необходимость их проверки, ясно, точно и грамотно выражать свои мысли в устной и письменной речи;
формирование умения использовать различные языки математики, свободно переходить с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства; интегрирование в личный опыт новой, в том числе самостоятельно полученной, информации;
создание условия для плодотворной работы в группе, умения самостоятельно и мотивированно организовывать свою деятельность, использовать приобретенные знания и умения в практической деятельности и повседневной жизни для исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств тел, вычисления площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Обязательный минимум содержания программы
Уравнения и неравенства
Равносильные уравнения и неравенства .Иррациональные уравнения. Показательные уравнения. Показательные неравенства. Системы показательных уравнений и неравенств. Логарифмические уравнения. Логарифмические неравенства.
Корни и степени
Степень с действительным показателем. Действительные числа. Арифметический корень натуральной степени. Степень с рациональным и действительным показателем. Логарифмы. Свойства логарифмов. Десятичные и натуральные логарифмы. Формула перехода.
Функции
Степенная функция, ее свойства и график. Взаимно обратные функции. Сложная функция. Дробно-линейная функция. Показательная функция, ее свойства и график. Логарифмическая функция, ее свойства и график.
Тригонометрия
Радианная мера угла. Поворот точки вокруг начала координат. Определение синуса, косинуса и тангенса угла. Знаки синуса, косинуса и тангенса угла. Зависимость между синусом, косинусом и тангенсом одного и того же угла. Тригонометрические тождества. Синус, косинус и тангенс углов α и –α. Формулы сложения. Синус, косинус и тангенс двойного угла. синус, косинус и тангенс половинного угла. Формулы приведения. Сумма и разность синусов. Сумма и разность косинусов. Произведение синусов и косинусов. Тригонометрические уравнения. Уравнения cosx=a. Уравнение sinx=a. Уравнение tgx=a. Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения. Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения.
Учебно-тематический план
-
№ пункта учебника
|
Изучаемые темы в курсе алгебры 10 класса
|
Количество часов
|
Дата проведения
|
Коррекция
|
Глава 4. Степень с действительным показателем
|
11
|
|
|
1
|
Действительные числа
|
1
|
|
|
|
Учебная цель – обобщение и систематизация знаний учащихся о расширении множества чисел (от натуральных до действительных); ознакомление с понятием предела последовательности
|
|
|
2
|
Бесконечно убывающая геометрическая прогрессия
|
2
|
|
|
|
Учебная цель – продолжить формирование представления о пределе числовой последовательности на примере изучения бесконечно убывающей геометрической прогрессии и нахождение ее суммы с помощью предела.
|
|
|
3
|
Арифметический корень натуральной степени
|
3
|
|
|
|
Учебная цель – обобщение знаний о корнях и арифметических корнях; подготовка к изучению понятия степени с действительным показателем.
|
|
|
4
|
Степень с рациональным и действительным показателями
|
3
|
|
|
|
Учебная цель – расширение понятия степени до степени с рациональным и действительным показателями; формирование навыков действий со степенями с рациональным показателем; изучение свойств степени с действительным показателем
|
|
|
1-4
|
Обобщающий урок по теме «Степень с действительным показателем»
|
1
|
|
|
|
Контрольная работа № 1 по теме «Степень с действительным показателем»
|
1
|
|
|
Глава 5. Степенная функция
|
13
|
|
|
1
|
Степенная функция, ее свойства и график
|
3
|
|
|
|
Учебная цель –знакомство учащихся с понятием ограниченной функции, со свойствами и графиками различных (в зависимости от показателя степени) видов степенной функции
|
|
|
2
|
Взаимно обратные функции. Сложная функция.
|
2
|
|
|
|
Учебная цель – ознакомление с понятием
взаимно обратных функций и сложных функций
|
|
|
3
|
Дробно-линейная функция
|
1
|
|
|
|
Учебная цель – ознакомить учащихся с дробно-линейной функцией, показать применение функции на примере прикладной задачи
|
|
|
4
|
Равносильные уравнения и неравенства
|
2
|
|
|
|
Учебная цель – введение понятий равносильности уравнений, неравенств, систем уравнений, а также уравнения-следствия; формирование у учащихся потребности при решении уравнений выполнять лишь те преобразования, которые не приводят к потери корней, а при решении неравенств осуществлять лишь равносильные преобразования
|
|
|
5
|
Иррациональные уравнения
|
2
|
|
|
|
Учебная цель – обучение решению иррациональных уравнений, возведением обеих его частей в одну и ту же натуральную степень; ознакомление с приемами решения систем, содержащих иррациональные уравнения
|
|
|
1-5
|
Обобщающий урок по теме «Степенная функция»
|
2
|
|
|
|
Контрольная работа № 2 по теме «Степенная функция»
|
1
|
|
|
Глава 6. Показательная функция
|
10
|
|
|
1
|
Показательная функция, ее свойства и график
|
2
|
|
|
|
Учебная цель – введение понятия показательная функция; демонстрация применения знаний о свойствах показательной функции к решению прикладных задач
|
|
|
2
|
Показательные уравнения
|
2
|
|
|
|
Учебная цель –овладение основными способами решения показательных уравнений
|
|
|
3
|
Показательные неравенства
|
2
|
|
|
|
Учебная цель – формирование умения решать показательные неравенства на основе свойства монотонности показательной функции
|
|
|
4
|
Системы показательных уравнений и неравенств
|
2
|
|
|
|
Учебная цель – обучение решению систем показательных уравнений; знакомство с решением систем, содержащих показательные неравенства
|
|
|
1-4
|
Обобщающий урок по теме «Показательная функция»
|
1
|
|
|
|
Контрольная работа № 3 по теме «Показательная функция»
|
1
|
|
|
Глава 7. Логарифмическая функция
|
15
|
|
|
1
|
Логарифмы
|
2
|
|
|
Учебная цель – введение понятия логарифма числа; знакомство с применением основного логарифмического тождества к вычислениям и решению простейших логарифмических уравнений
|
|
|
2
|
Свойства логарифмов
|
2
|
|
|
Учебная цель – изучение основных свойств логарифмов о формирование умений их применения для преобразования логарифмических выражений
|
|
|
3
|
Десятичные и натуральные логарифмы
|
2
|
|
|
Учебная цель – введение понятий десятичного и натурального логарифмов, обучение применению формулы перехода от логарифма по одному основанию к логарифму по другому основанию
|
|
|
4
|
Логарифмическая функция, ее свойства и график
|
2
|
|
|
Учебная цель – обоснование свойств логарифмической функции и построение ее графика; демонстрация применения свойств логарифмической функции при сравнении значений выражений и решение простейших логарифмических уравнений и неравенств
|
|
|
5
|
Логарифмические уравнения
|
2
|
|
|
Учебная цель – формирование умений решать различные логарифмические уравнения и их системы с использованием свойств логарифмов и общих методов решения уравнений
|
|
|
6
|
Логарифмические неравенства
|
2
|
|
|
Учебная цель – обучение решению логарифмических неравенств на основании свойств логарифмической функции
|
|
|
1-6
|
Обобщающий урок по теме «Логарифмическая функция»
|
2
|
|
|
|
Контрольная работа № 4 по теме «Логарифмическая функция»
|
1
|
|
|
Глава 8. Тригонометрические формулы
|
20
|
|
|
1
|
Радианная мера угла
|
1
|
|
|
Учебная цель – ознакомление с соответствием между точками числовой прямой и окружности, формирование понятия радиана
|
|
|
2
|
Поворот точки вокруг начала координат
|
2
|
|
|
Учебная цель – формирование понятия поворота точки единичной окружности вокруг начала координат на угол α и обучение нахождению положения точки окружности, соответствующей данному действительному числу
|
|
|
3
|
Определение синуса, косинуса и тангенса угла
|
2
|
|
|
Учебная цель – введение понятия синуса, косинуса, тангенса и котангенса угла(числа); обучение их нахождению для чисел вида 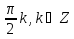 ; ознакомление с применением определение синуса и косинуса при решении простейших тригонометрических уравнений ; ознакомление с применением определение синуса и косинуса при решении простейших тригонометрических уравнений
|
|
|
4
|
Знаки синуса, косинуса и тангенса угла
|
1
|
|
|
Учебная цель – обучение нахождению знаков значений синуса, косинуса, тангенса и котангенса угла
|
|
|
5
|
Зависимость между синусом, косинусом и тангенсом одного и того же угла
|
2
|
|
|
Учебная цель – вывод формулы зависимости между синусом, косинусом и тангенсом одного и того же угла (числа); обучение применению этих формул для вычисления значений синуса, косинуса, тангенса числа по заданному значению одного из них
|
|
|
6
|
Тригонометрические тождества
|
2
|
|
|
Учебная цель – ознакомление с понятием тождества как равенства, справедливого для всех допустимых значений букв; обучение доказательству тождеств с использованием изучаемых формул
|
|
|
7
|
. Синус, косинус и тангенс углов α и –α
|
1
|
|
|
Учебная цель – обучение сведению вычислений синуса, косинуса, тангенса отрицательных углов к вычислению их значений для положительных углов
|
|
|
8
|
Формулы сложения
|
2
|
|
|
Учебная цель – обучение применению формул сложения при вычислениях и выполнении преобразований тригонометрических выражений
|
|
|
9
|
Синус, косинус и тангенс двойного угла
|
1
|
|
|
10
|
Синус, косинус и тангенс половинного угла
|
1
|
|
|
Учебная цель – ознакомление учащихся со следствиями теоремы сложения; обучение применению формул двойного угла при преобразованиях тригонометрических выражений, в частности при выводе формул половинного угла
|
|
|
11
|
Формулы приведения
|
2
|
|
|
Учебная цель – обучение применению правила, позволяющего заменить синус, косинус, тангенс, котангенс любого числа соответственно синусом, косинусом, тангенсом или котангенсом числа α, если 0<α<
|
|
|
12
|
Сумма и разность синусов. Сумма и разность косинусов
|
1
|
|
|
Учебная цель – ознакомление учащихся с применением формул для разложения тригонометрических выражений на множители
|
|
|
1-12
|
Обобщающий урок по теме «Тригонометрические формулы»
|
1
|
|
|
|
Контрольная работа № 5 по теме «Тригонометрические формулы»
|
1
|
|
|
Глава 9. Тригонометрические уравнения
|
15
|
|
|
1
|
Уравнение cosx=a
|
3
|
|
|
Учебная цель – знакомство с понятием арккосинуса числа; обучение решению простейших тригонометрических уравнений
|
|
|
2
|
Уравнение sinx=a
|
3
|
|
|
Учебная цель – ознакомление с понятием арксинуса числа; обучение решению уравнений, сводящихся к уравнению sinx=a
|
|
|
3
|
Уравнение tgx=a
|
2
|
|
|
Учебная цель – знакомство с понятием арктангенса числа; обучение решению уравнения вида tgx=a
|
|
|
4
|
Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения
|
3
|
|
|
Учебная цель – обучение решению тригонометрических уравнений, сводящихся к алгебраическим уравнениям; решение однородных уравнений первой и второй степеней
|
|
|
5
|
Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения
|
2
|
|
|
Учебная цель – знакомство с применением метода разложения на множители для решения тригонометрических уравнений; знакомство с оценочным методом при решении тригонометрических уравнений
|
|
|
1-5
|
Обобщающий урок по теме «Тригонометрические уравнения»
|
1
|
|
|
|
Контрольная работа № 6 «Тригонометрические уравнения»
|
1
|
|
|
Заключительный урок по курсу алгебры и начала анализа 10 класса
|
1
|
|
|
Итого:
|
85
|
|
|
Требования к уровню подготовки учащихся 10 класса
В результате изучения математики на базовом уровне ученик должен
Знать/понимать:
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике, для формирования и развития математической науки; историю развития понятия числа, создание математического анализа, возникновение и развитие геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях деятельности;;
вероятностный характер различных процессов окружающего мира;
Алгебра
Уметь:
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значение корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки преобразования;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства;
Функции и графики
Уметь:
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изучаемых функций;
описывать по графику и в простейших случаях по формуле поведения и свойства функций, находить по графику функции наибольшее и наименьшее значения;
решать уравнения, простейшие системы уравнений, , используя свойства функции и их графиков;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков;
Начала математического анализа
Уметь:
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшее и наименьшее значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для решения прикладных задач, в том числе социально-экономических и физических, на наибольшее и наименьшее значения, на нахождение скорости и ускорения;
Уравнения и неравенства
Уметь:
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
Использовать приобретенные знания и умения в практической деятельности и повседневной жизни:
для построения и исследования простейших математических моделей;
анализа реальных числовых данных, представленных в виде диаграмм, графиков;
анализа информации статистического характера;
владеть компетенциями: учебно-познавательной, ценностно-ориентационной, рефлексивной, коммуникативной, информационной, социально-трудовой.
Система контролирующих материалов
Контрольная работа № 1 по теме «Степень с действительным показателем»
Контрольная работа № 2 по теме «Степенная функция»
Контрольная работа № 3 по теме «Показательная функция»
Контрольная работа № 4 по теме «Логарифмическая функция»
Контрольная работа № 5 по теме «Тригонометрические формулы»
Контрольная работа № 6 «Тригонометрические уравнения»
Условные обозначения уровней обучения и освоения системы знаний:
Б –базовый (опорный)
Р – репродуктивный;
П – повышенный (функциональный);
ПР – продуктивный
ТВ – творческий;
И – исследовательский.
|
|
|
 Скачать 0.68 Mb.
Скачать 0.68 Mb. ; ознакомление с применением определение синуса и косинуса при решении простейших тригонометрических уравнений
; ознакомление с применением определение синуса и косинуса при решении простейших тригонометрических уравнений