|
Техника дифференцирования
Урок «Алгебра и начала анализа » 10 класс.
Тема: Техника дифференцирования.
Цели урока:
Общеобразовательные:
Развивающие:
развитие математического кругозора, мышления, речи, внимания и памяти.
Воспитательные:
Учебник: А.Н. Колмогоров Алгебра и начала анализа, учебник для 10-11 кл.
Ход урока
1.Орг. момент.
Здравствуйте, садитесь! Мы изучили правила вычисления производных функций. Как вы думаете, хорошо ли вы умеете вычислять производные функций? Хотите ли вы закрепить ваши навыки?
Сформулируйте цель урока.
Сегодня мы будем работать над закреплением техники дифференцирования. (слайд 1)
|
Здравствуйте.
Хорошо бы еще закрепить навыки.
Повторить, закрепить навыки нахождения производных.
|
2.Устная работа. Для начала необходимо вспомнить формулы и правила дифференцирования.
1.(Устно) Найдите производную каждой функции (слайд 2)
Х; х²; х³; √х;
1/х; С; (кх+в);
Sinx; Cosx; tgx ; ctgx ;
f(g(x))
2. Продолжите формулу (слайд 3)
(u+v)'=
(uv)' =
(u/v)' =
(Cu)' =
3. Составьте сложную функцию (Большая стрелка – «главная» функция, маленькая стрелка – «подчиненная функция») и найдите ее производную. (наглядность часы). Приложение.
Например у=sin(√x), y'=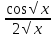 . .
|
1, 2х, 3х², 1/(2√х),
-1/х², 0, к,
Cosx, -Sinx, 1/cos²x, -1/sin²x
F '(g(x))·g '(x)
u'+v', u'v+uv', 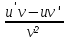 , Cu' , Cu'
|
3. Работа в парах.
Это задание нужно выполнить парой. Предложенные функции распределите в соответствующие колонки. (Слайд 4, 5).В колонках запишите только номер функции. (Раздаю карточки с таблицей)
|
|
4. Игра «Поле чудес». Учащиеся получают карточки с заданием. На доске заготовлена таблица и шифр. Учащиеся, выполнив задание, вписывают букву, соответствующую полученному ответу, в клеточку с номером, указанным на карточке. Последнее слово ученики отгадывают, когда заполнены все остальные клетки (это слово – ЕГЭ).
1
|
10
|
3
|
2
|
18
|
5
|
|
19
|
|
16
|
9
|
6
|
13
|
11
|
7
|
|
20
|
14
|
12
|
4
|
8
|
|
15
|
17
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Шифр:
а
|
В
|
г
|
е
|
ж
|
к
|
л
|
н
|
О
|
т
|
у
|
ч
|
ь
|
я
|
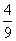
|
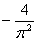
|
3
|
0
|
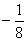
|
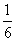
|
-2
|
-3
|
1
|
2
|
136
|
5
|
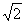
|
4
|
Задания на карточках:
Найдите значение производной в точке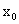 : :
у = 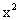 + 2х – 1, + 2х – 1, 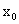 = 0 = 0
Найдите значение производной в точке х0:
у = х3 - 3х + 2, х0 = -1
Найдите значение производной в точке х0:
У=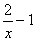 , х0 = 4 , х0 = 4
Найдите значение производной в точке х0:
у = 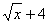 , х0 = 9 , х0 = 9
Найдите значение производной в точке х0:
у = cos x + tg x, x0 = π
Найдите значение производной в точке х0:
y = (x2 + 3)(x4 – 1), x0 = 0
Найдите значение производной в точке х0:
y = (x2 - 2)(x7 + 4), x0 = 0
Найдите значение производной в точке х0:
y = x sin x, x0 = 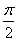
Найдите значение производной в точке х0:
у = 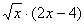 , х0 = 4 , х0 = 4
Найдите значение производной в точке х0:
у = 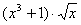 , х0 = 1 , х0 = 1
Найдите значение производной в точке х0:
у =sin x – cos x, х0 = 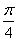
Найдите значение производной в точке х0:
у = 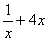 , х0 = 1 , х0 = 1
Найдите значение производной в точке х0:
у = 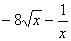 , х0 = 1 , х0 = 1
Найдите значение производной в точке х0:
у = 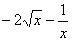 , х0 = 1 , х0 = 1
Найдите значение производной в точке х0:
у = 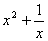 , х0 = -1 , х0 = -1
Найдите значение производной в точке х0:
у = x6 + 13x10 + 12, х0 = 1
Найдите значение производной в точке х0:
у = 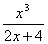 , х0 = 1 , х0 = 1
Найдите значение производной в точке х0:
у = 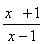 , х0 = 2 , х0 = 2
Найдите значение производной в точке х0:
у = 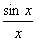 , х0 = , х0 = 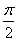
Найдите значение производной в точке х0:
у = 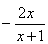 , х0 = 0 , х0 = 0
- Тяжело в ученье, легко на ЕГЭ.
|
|
4. Самостоятельная работа с самопроверкой. Решить самостоятельную работу. Взять ответы, проверить. Если есть ошибки взять карточки с решением. Проанализировать. Оценить себя.
В-1. Вычислите значения производных функций при заданных значениях аргумента:
у=2х(4) – 5х³+2х-5, х°=-2;
у=3sinx+2, x°=  ; ;
y=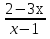 , x°=2; , x°=2;
y= √tg3x, x°=
В-2. Вычислите значения производных функций при заданных значениях аргумента:
у=4х³+6х+3, х°=1;
у=3cosx -2, x°=  . .
y=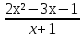 , x°=1; , x°=1;
y= 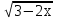 , x°=1. , x°=1.
|
|
Итог урока.
Оценивание.
Домашнее задание: Составить карточки с 5 заданиями на нахождение производной. №238.
|
| |
|
|
 Скачать 77.44 Kb.
Скачать 77.44 Kb.