«Решение логарифмических уравнений»
 Скачать 63.32 Kb. Скачать 63.32 Kb.
|
| Тема урока: « Решение логарифмических уравнений ». Цели урока: вспомнить и систематизировать виды логарифмических уравнений, основные способы решений логарифмических уравнений. Задачи урока: а) обучающая - формирование знаний о свойствах логарифмической функции и применении их в решении логарифмических уравнений; итоговая отработка способов и методов их решения; б) развивающая - развитие навыков самоконтроля при решении заданий; развитие навыков взаимоконтроля; в) воспитательная - формирование грамотной устной и письменной математической речи учащихся, воспитание ответственного отношения к учебному труду; воспитание чувства коллективизма. Оборудование: компьютер, мультимедийный проектор, экран. Ход урока: 1. Сообщение целей урока и его плана. 2. а) ответы на вопросы по домашней работе по предыдущей теме(6-7 минут); б) устная работа по вопросам теории, заданным также на дом: 1. Определение логарифма, натуральный и десятичный логарифмы, примеры; 2. Основное логарифмическое свойство, примеры; 3. Формула логарифма произведения, примеры; 4. Формула логарифма частного, примеры; 5. Формула логарифма степени, примеры; 6. Формула перехода от одного основания логарифма к другому, примеры; 7. Об области определения и монотонности логарифмической функции. 3. Систематизация знаний и умений с использованием заранее заготовленных заданий (30 минут). Учитель проектирует на экран задание, учащиеся вместе с учителем обсуждают типы уравнений и методы их решений. Затем решают в тетрадях. После чего, учитель проектирует на экран решение и окончательный ответ. В ходе проверки комментируются все применяемые свойства и определения. Блок№1. Простейшие уравнения. а) log 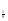 (2x2 - 2x - 1) = - (2x2 - 2x - 1) = - 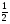  . .По определению логарифма получаем уравнение 2х2 – 2х – 1 = ( 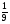 ) )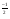  2х2 – 2х -1 = 3 2х2 – 2х -1 = 3  х2 – х – 2 = 0. Ответ: -1; 2. б) log25[ 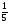 log3(2 – log0,5 x)] = - log3(2 – log0,5 x)] = - 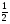 . .По определению логарифма получаем уравнение 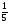 log3(2 – log0,5 x) = 25-0,5 log3(2 – log0,5 x) = 25-0,5 log3(2 – log0,5x) = 1. Вновь используем определение логарифма: 2 - log0,5 x = 31 , откуда log0,5 x = - 1 log3(2 – log0,5x) = 1. Вновь используем определение логарифма: 2 - log0,5 x = 31 , откуда log0,5 x = - 1 Получаем х = ( 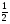 )-1 = 2. Ответ: 2. )-1 = 2. Ответ: 2.в) log3 (x2 – 4) = log3 (4x – 7). Особенностью логарифмических уравнений является появление посторонних корней. Это связано с расширением ОДЗ уравнения в ходе его преобразования. Поэтому полученные корни необходимо проверять подстановкой. ОДЗ данного уравнения задаётся неравенствами 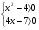 . Решая эту систему неравенств получаем ОДЗ уравнения х . Решая эту систему неравенств получаем ОДЗ уравнения х (2; ∞). (2; ∞).Логарифмическое уравнение заменяем ему равносильным: х2 – 4х + 3 = 0, которое имеет корни х1 = 1 и х2 = 3. После проверки выявляется посторонний корень х = 1. Ответ: 3. Блок № 2. Уравнения, решаемые их преобразованиями. а) 2log3(x – 2) – log3(x2 – 4x + 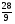 ) = 2. ) = 2.ОДЗ: 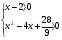 . Сведём данное уравнение к простейшему: . Сведём данное уравнение к простейшему:  log3(x – 2)2 – log3(x2 – 4x + log3(x – 2)2 – log3(x2 – 4x + 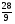 ) = 2 ) = 2  log3 log3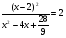  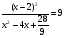 . После преобразований получим квадратное уравнение: х2 – 4х + 3 = 0, которое имеет корни . После преобразований получим квадратное уравнение: х2 – 4х + 3 = 0, которое имеет корни х1 = 1 и х2 = 3. После проверки выявляется посторонний корень х = 1. Ответ: 3. б) log2 x + log4 x + log8 x = 5,5. Одним из распространённых преобразований является переход к новому основанию в логарифмах: logcb= 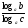 . .В логарифмах перейдём к одному основанию, например числу 2. log2 x + 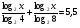  log2 x + log2 x + 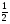 log2 x + log2 x + 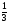 log2 x = 5,5 log2 x = 5,5  6 log2 x + 3 log2 x + 2log2 x = 33 6 log2 x + 3 log2 x + 2log2 x = 33  11∙ log2 x = 33 11∙ log2 x = 33  log2 x = 3 log2 x = 3  x = 23 = 8. Ответ: 8. x = 23 = 8. Ответ: 8.Блок № 3. Уравнения, решаемые разложением на множители. Переносим все члены уравнения в левую часть, проводим группировку и раскладываем на множители: 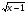 log2 (3х2 – 5) + 2 = log2 (3х2 – 5) + 2 log2 (3х2 – 5) + 2 = log2 (3х2 – 5) + 2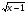 , ,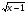 log2 (3х2 – 5) + 2 - log2 (3х2 – 5) - 2 log2 (3х2 – 5) + 2 - log2 (3х2 – 5) - 2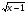 = 0, = 0,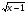 log2 (3х2 – 5) - log2 (3х2 – 5) + (2 - 2 log2 (3х2 – 5) - log2 (3х2 – 5) + (2 - 2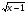 ) = 0, ) = 0,(log2 (3х2 – 5) – 2)( 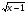 - 1) = 0. - 1) = 0.Произведение множителей равно нулю, если один из них равен нулю. Получаем два уравнения, которые надо решать, не забывая об ОДЗ уравнения, а именно 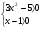 . .1) log2 (3х2 – 5) – 2 = 0  log2 (3х2 – 5) = 2 log2 (3х2 – 5) = 2  3х2 – 5 = 4 3х2 – 5 = 4  х2 = 3 х2 = 3  х = х = 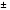 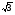 . .В ОДЗ входит только х = 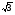 ; ;2) 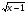 - 1 = 0 - 1 = 0  х – 1 = 1 х – 1 = 1  х = 2. х = 2.Ответ: 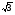 ; 2. ; 2.Блок № 4. Уравнения, решаемые с помощью замены переменной. а) log22(2x – 1) + log2(2x -1) – 2 = 0. Проведём замену у = log2(2x -1) и получим квадратное уравнение у2 + у – 2 = 0. Его корни 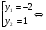 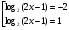  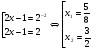 . Оба корня входят в ОДЗ уравнения. Ответ: . Оба корня входят в ОДЗ уравнения. Ответ: 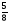 ; ; 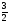 . .б) 4 – lg x = 3 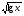 . Проведём замену lg x = у, тогда данное уравнение примет вид у2 + 3у – 4 = 0, корни уравнения у1 = 1, у2 = -4(посторонний корень). Следовательно, . Проведём замену lg x = у, тогда данное уравнение примет вид у2 + 3у – 4 = 0, корни уравнения у1 = 1, у2 = -4(посторонний корень). Следовательно, 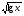 = 1, откуда х = 10. = 1, откуда х = 10.Ответ: 10. Блок № 5. Уравнения, решаемые с помощью их специфики. Встречаются задачи, решение которых основано на свойствах входящих в них функций. log2 x = 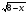 . Исследуем монотонность функций, входящих в уравнение. Функция у1 = log2 x – возрастающая, функция у2 = . Исследуем монотонность функций, входящих в уравнение. Функция у1 = log2 x – возрастающая, функция у2 = 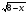 - убывающая. Корень уравнения – единственный, это точка пересечения графиков этих функций. Корень уравнения подбираем (угадываем). - убывающая. Корень уравнения – единственный, это точка пересечения графиков этих функций. Корень уравнения подбираем (угадываем).Ответ: 4. а) приём логарифмирования: 3х = х 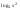 , найдём логарифм по основанию 3 от обеих частей данного уравнения и используем свойства логарифмов. Получаем: log3 (3x) = log3 (xlog , найдём логарифм по основанию 3 от обеих частей данного уравнения и используем свойства логарифмов. Получаем: log3 (3x) = log3 (xlog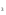 x x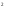 ) )  log3 3 + log3 x = log3 x2 ∙ log3 x  1 + log3 x = 2log32x . Введём новую переменную 1 + log3 x = 2log32x . Введём новую переменнуюу = log3 x и получим квадратное уравнение 1 + у = 2у2  2у2 – у – 1 = 0, у1 = 1, у2 = - 2у2 – у – 1 = 0, у1 = 1, у2 = - 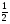 . .Вернёмся к х: 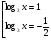  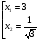 . Ответ: 3; . Ответ: 3; 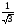 . .б) применение основного логарифмического тождества: 3 х 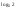 + 2 + 2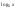 = 64. = 64.Запишем х в виде х = 5 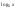 =( 2 =( 2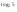 ) )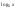 = 2 = 2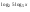 . Данное уравнение приведётся к виду . Данное уравнение приведётся к виду3∙ 2 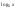 + 2 + 2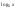 = 64 = 64  4 ∙ 2 4 ∙ 2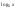 = 64 = 64  log5 x = 4. Ответ: 625. log5 x = 4. Ответ: 625.Блок № 6. Уравнения, решаемые графически. Определить число корней и найти меньший из них log0,5 x = -x2 + 2x – 1. Построим графики функций у1 = log0,5 x , у2 = -(х – 1)2. Графики пересекаются в точках А и В. Следовательно, уравнение имеет два корня. Абсцисса точки А меньше абсциссы точки В. Поэтому меньший корень уравнения х = 1. Ответ: 2 корня, меньший из них 1. 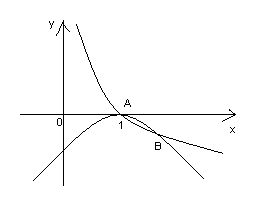 4. Подведение итогов урока. Выставление оценок наиболее активным ученикам, консультанты тоже принимают участие в оценке работы членов своей группы. 5. Постановка домашнего задания: на экране – логарифмические уравнения: № 1. 2 + 6 log8 x = log2 ( 6x + 18). № 2. lg (x + 4) + lg (2x + 3) = lg ( 1 – 2x). № 3. log2 x + log4 x + log16 x = 7. № 4. х 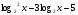 = =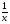 . .Ответы: №1 (3); №2 (-1); №3 (16); №4 (1; 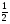 ; 16). ; 16).Необходимо взять несколько заданий из учебника, подойдя к ним дифференцированно. В домашнюю работу можно включить творческие задания, уравнения такого типа как, а) log3 x ∙ log9 x ∙ log27 x ∙ log81 x = 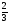 ; ;б) log2 x + log4 x + log8 x = 11; в) х 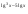 = 0, 0001; = 0, 0001;г) logх3 + log3 x = log 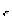 3 + log3 3 + log3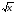 + 0, 5. + 0, 5.Ответы: а) 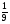 ; 9, б)64, в)10-2; 10-1; 10; 100, г)2. ; 9, б)64, в)10-2; 10-1; 10; 100, г)2.Следующий урок по теме «Решение логарифмических уравнений и неравенств» будет посвещён решению логарифмических неравенств. В начале урока проводится проверочная работа на 10-12 минут, в которую можно включить уравнения, которые решаются уже известными методами, использованными на прошлом уроке и при выполнении домашней работы. Приведу пример одного варианта такой проверочной работы: № 1. Решить уравнение: 2 log0,5 x = log0,5 (2x2 – x); № 2. Решить уравнение: (х2 + х – 2) log 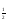 (3х – 2) = 0; (3х – 2) = 0; № 3. Решить уравнение: lоg4(lоg3(lоg2(х2 + 7х))) = 0; № 4. Найдите все значения параметра а, при которых уравнение (х – а) log2 х = 0 имеет единственное решение. № 5. Выберите наибольшее решение уравнения: 2 log32 х - 7 log3 х = - 3. Дополнительно: log2x+1(5 + 8x – 4x2) + log5-2x(1 + 4x + 4x2) = 4. Ответы: №1 (1); №2 (1); №3 (-8; 1); №4 ( (-∞; 0) 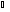  );№5 (27);доп.( );№5 (27);доп.(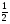 ; 1). ; 1).Согласно тематическому планированию на тему «Решение логарифмических уравнений и неравенств» отводится пять уроков, после которых можно провести тематическую контрольную работу по своей структуре похожей на ЕГЭ, что является некоторым этапом подготовки к этому испытанию. Приведу один вариант такой контрольной работы: В1. Упростить выражение 2 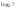 + log575 - log53. + log575 - log53.В2. Указать промежуток, которому принадлежит корень уравнения log2 (х + 1) = 4. В3. Решить неравенство log0,4(1,9х – 1, 3) ≥ - 1. В4. Найти сумму корней уравнения log 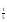 4x + log5 (x2 + 75) = 1. 4x + log5 (x2 + 75) = 1.B5. Найти число целых решений неравенства log22х - log2х ≤ 6. С1. Пусть (х0; у0) – решение системы 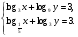 Найти отношение Найти отношение 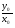 . .С2. Решите уравнение lg x2 + lg (x + 10)2 = 2 lg 11. C3. Решите неравенство (х – 1) log 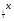 + + 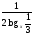 ≥ 0. ≥ 0.Ответы: В1.1. В2.2. В3.1. В4.20. В5.8. С1.27. С2 -11; 1; -5 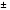 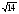 . С3.(0,5; 1) . С3.(0,5; 1) |