Прямоугольная система координат на плоскости (6 класс)
 Скачать 15.37 Kb. Скачать 15.37 Kb.
|
Дидактическая игра «Из поля в лес»Тема: Прямоугольная система координат на плоскости (6 класс). Цель: создать условия для проверки у учащихся умений строить точки по заданным координатам и находить координаты заданных точек. ХОД ИГРЫ В игре участвуют две команды. Одна команда выступает за лесничего, другая — за волка. Используется координатная доска, игральная кость (кубик, на гранях которого нанесены цифры 1, 2, 3, 4, 5, 6), две фишки (разные по цвету картонные кружки). К доске выходят поочередно по одному ученику от команды. Игру начинает «лесничий». Он подбрасывает кость 2 раза и после этого передвигает фишку по горизонтали настолько единиц, сколько содержит цифра на верхней грани кубика при первом броске, а по вертикали настолько единиц, сколько единиц содержит цифра на верхней грани кубика при втором броске. Двигаться вправо или влево, вверх или вниз — решает сам «лесничий». В начале игры оба участника находятся в начале координат. «Волк», учитывая передвижение, которое выполнил лесничий, должен сделать прыжок в точку, алгебраическая сумма координат которой равна сумме координат точки, в которую встал лесничий. «Волк» выигрывает, если убежит с поля в лес, «лесничий» — если поймает «волка», т. е. станет в ту точку координат, что и «волк». Лес 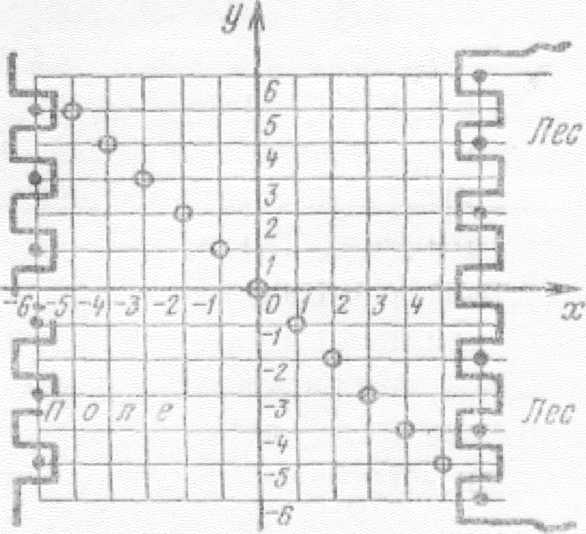 На рисунке изображены кружочки. Это ловушки, которые расставил «лесничий» на «волка». Если «волк» попадет в такую ловушку, выигрывает также «лесничий». Ловушки расставлены вдоль прямой у= -х, т. е. находятся в точках, в которых сумма координат равна нулю. Если «лесничий» хочет загнать «волка» в ловушку, он должен переместиться так, чтобы сумма координат в этой точке равнялась 0, например, в точке (- 3; 3). Это возможно, если оба раза при подбрасывании получить одну и ту же цифру. Невнимательный лесничий может не учесть такую ситуацию. Для одного хода выполняется два броска. За игрой следит весь класс. Для очередного хода вызываются новые "волк" и "лесничий" из каждой команды. |