Теорема:
Уравнение Ферма
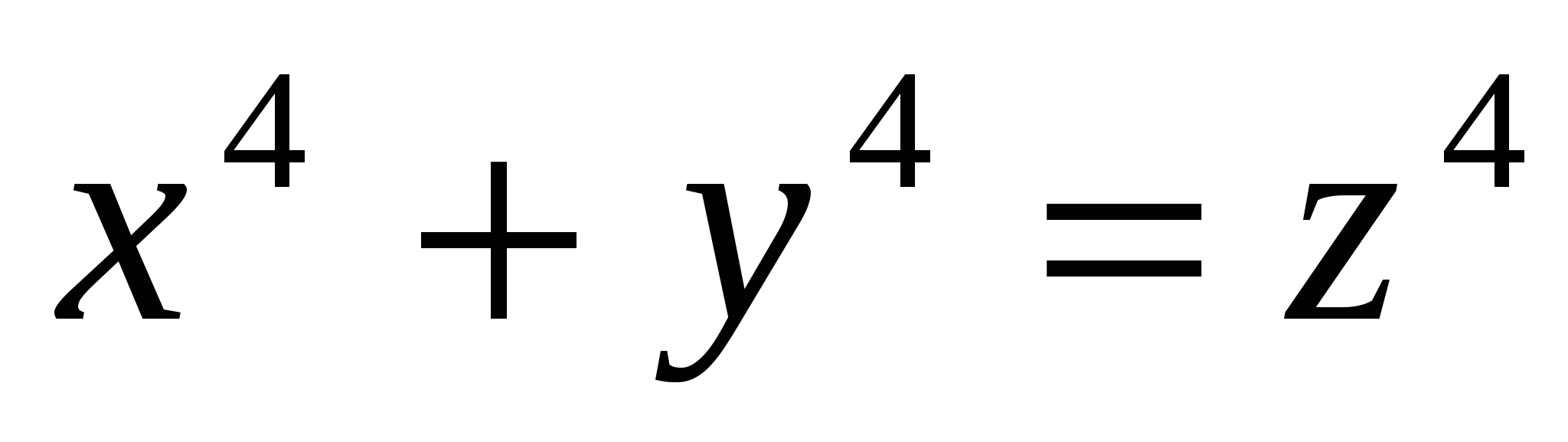 (1) (1)
не имеет решений в целых числах x, y и z, xyz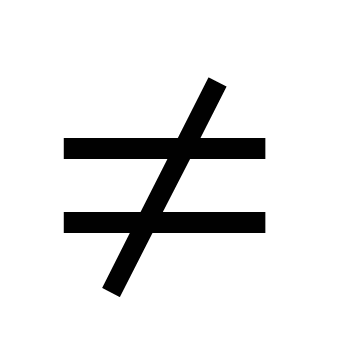 0. 0.
Доказательство: Мы докажем даже более сильную теорему, именно, что уравнение
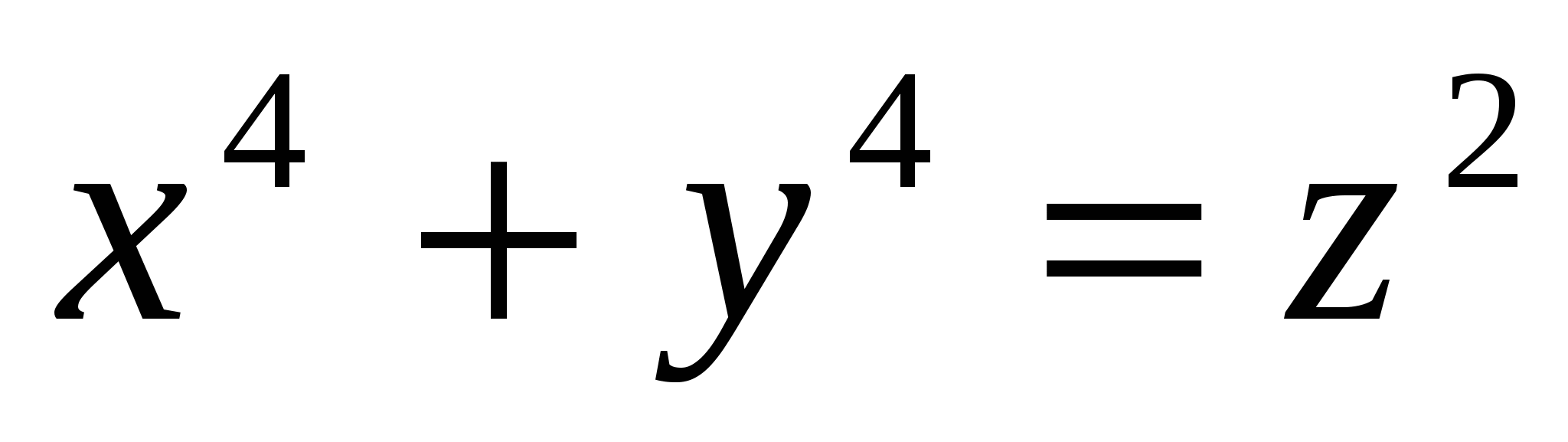 (2) (2)
не имеет решений в целых числах x, y и z, xyz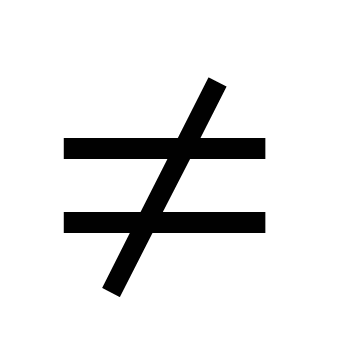 0. 0.
Из этой теоремы уже следует непосредственно отсутствие решений у уравнения (1). Если уравнение (2) имеет решение в целых, отличных от нуля числах x, y, z, то можно предполагать, что эти числа попарно взаимно просты. Действительно, если есть решение, в котором числа x и y имеют наибольший общий делитель d>1, то

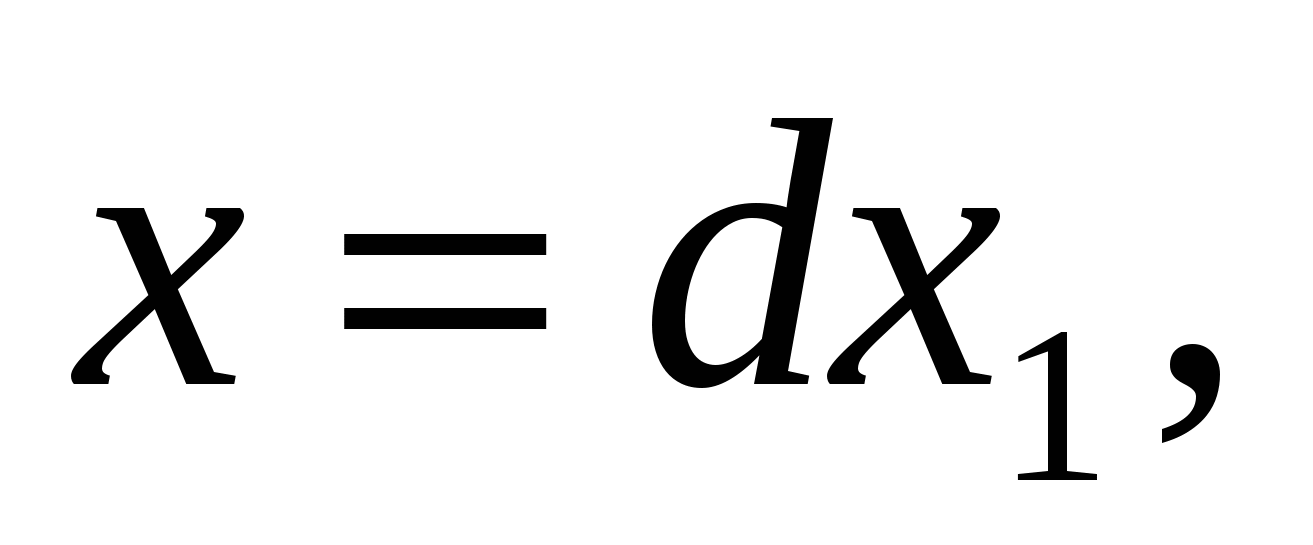 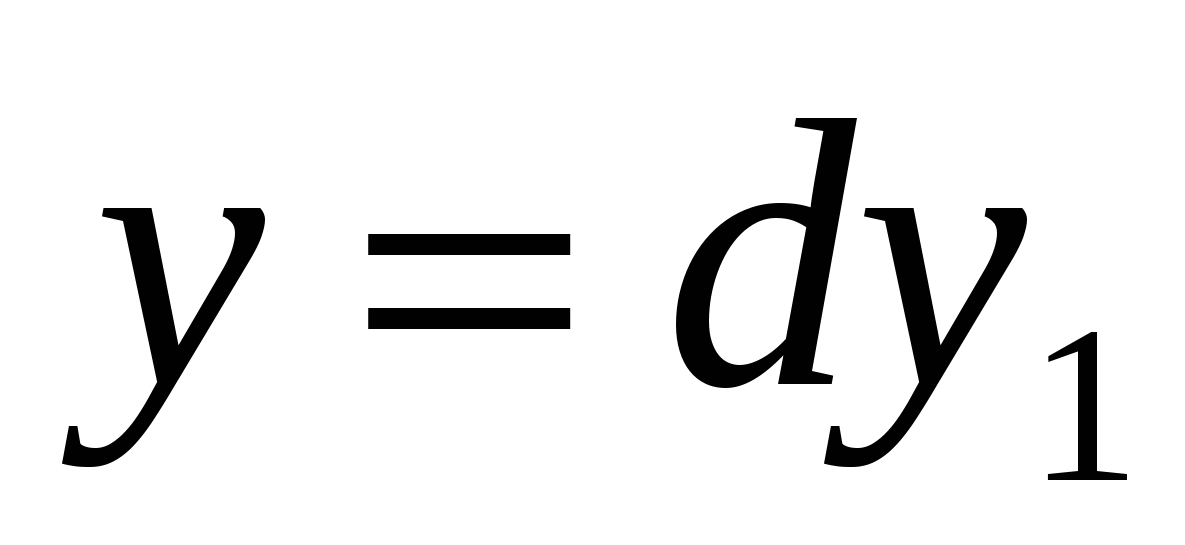 , ,
где (x1, y1)=1. Разделив обе части уравнения (2) на d4, мы будем иметь, что
x14+y14 =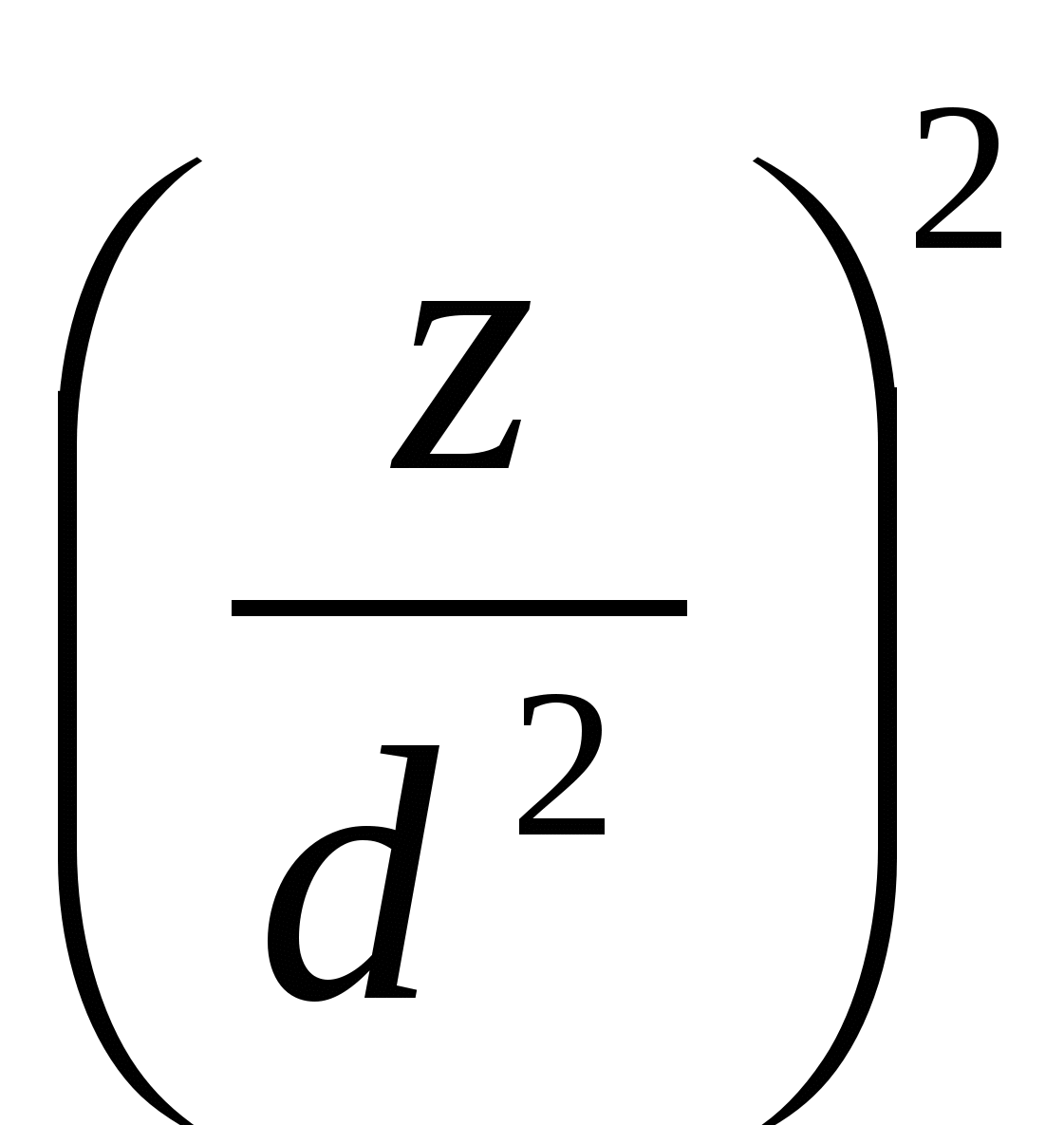 = z12. (3) = z12. (3)
Но x1 и y1 – целые числа, значит, 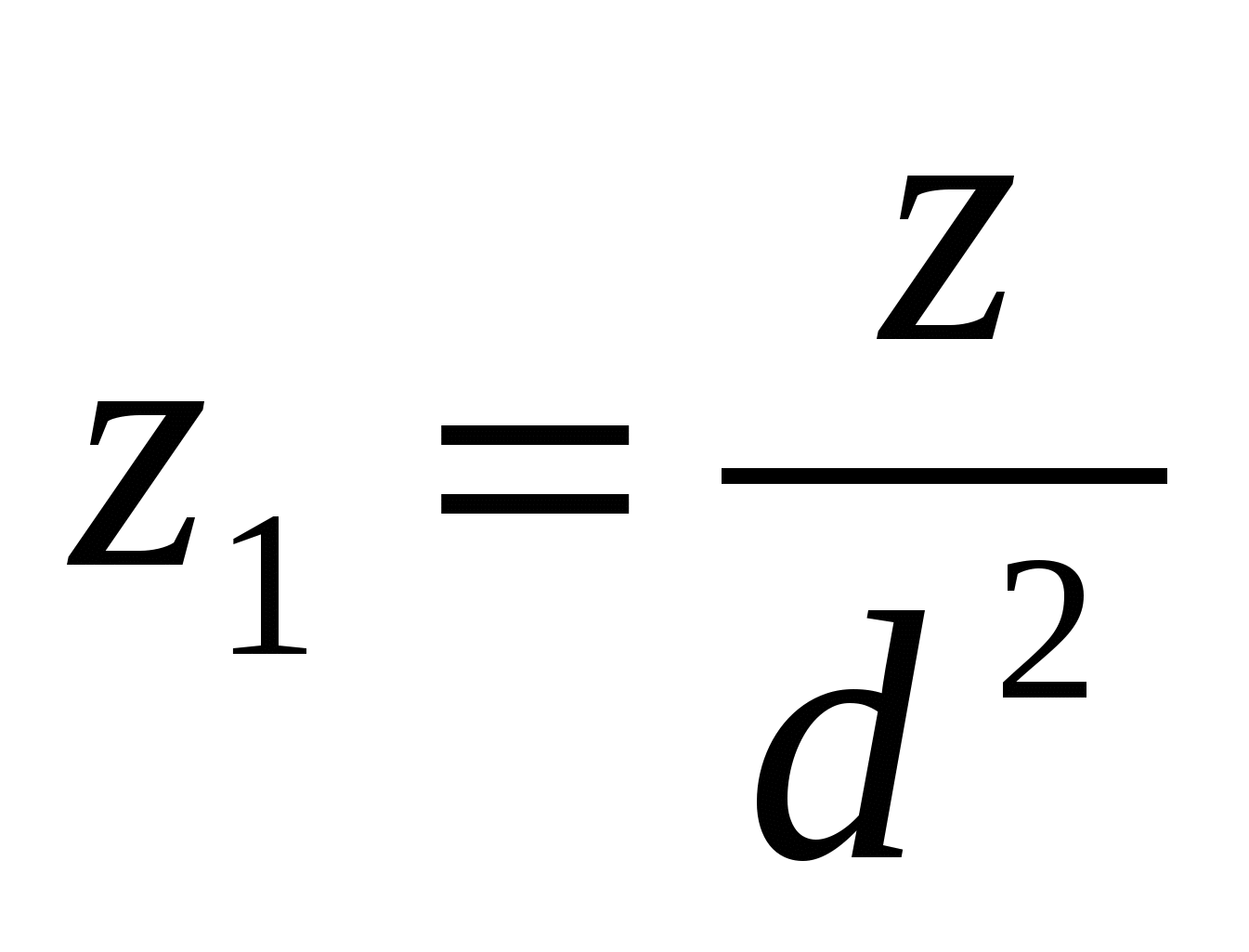 - тоже целое число. Если бы у z1 и y1 был общий делитель k>1, то x12 в силу (3) должно было бы делиться на k, а значит, - тоже целое число. Если бы у z1 и y1 был общий делитель k>1, то x12 в силу (3) должно было бы делиться на k, а значит, 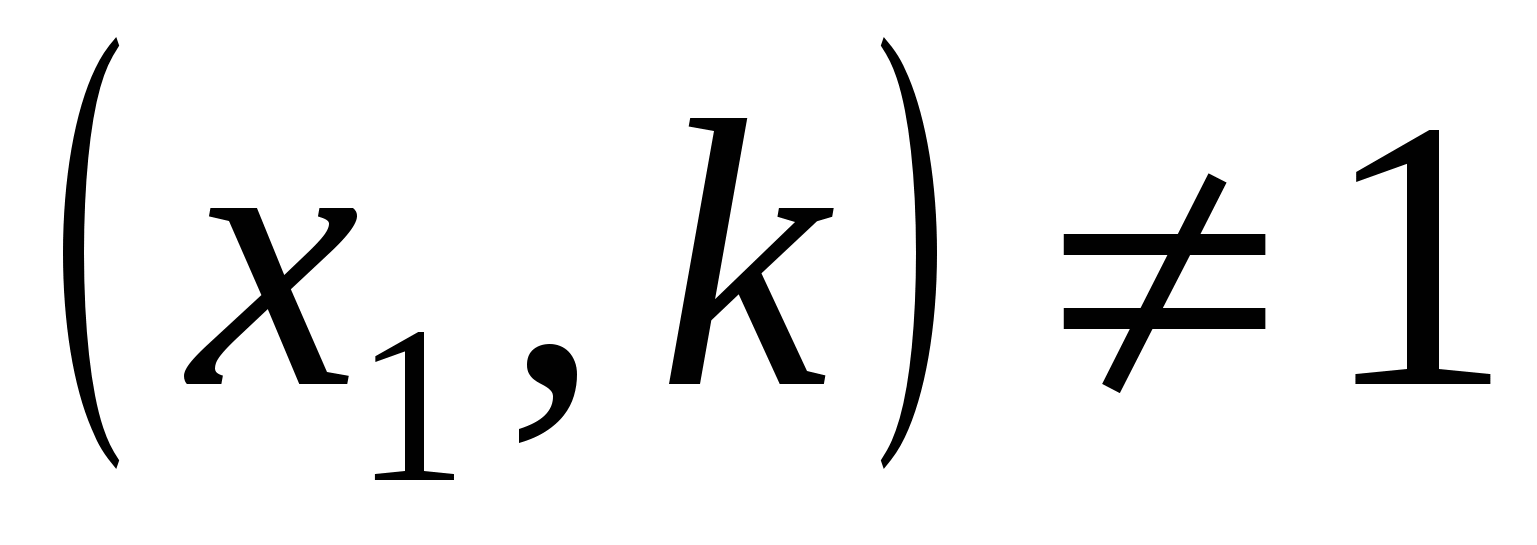 . Итак, мы доказали, что если существует решение уравнения (2) в целых, отличных от нуля числах, то существует также решения в целых, отличных от нуля и взаимно простых числах. Поэтому нам достаточно доказать, что уравнение два не имеет решений в целых, отличных от нуля и попарно взаимно простых числах. В дальнейшем ходе доказательства мы, говоря, что уравнение (2) имеет решение, будем предполагать, что оно имеет решение в целых, положительных и попарно взаимно простых числах. . Итак, мы доказали, что если существует решение уравнения (2) в целых, отличных от нуля числах, то существует также решения в целых, отличных от нуля и взаимно простых числах. Поэтому нам достаточно доказать, что уравнение два не имеет решений в целых, отличных от нуля и попарно взаимно простых числах. В дальнейшем ходе доказательства мы, говоря, что уравнение (2) имеет решение, будем предполагать, что оно имеет решение в целых, положительных и попарно взаимно простых числах.
В §4 мы доказали, что все решения уравнения 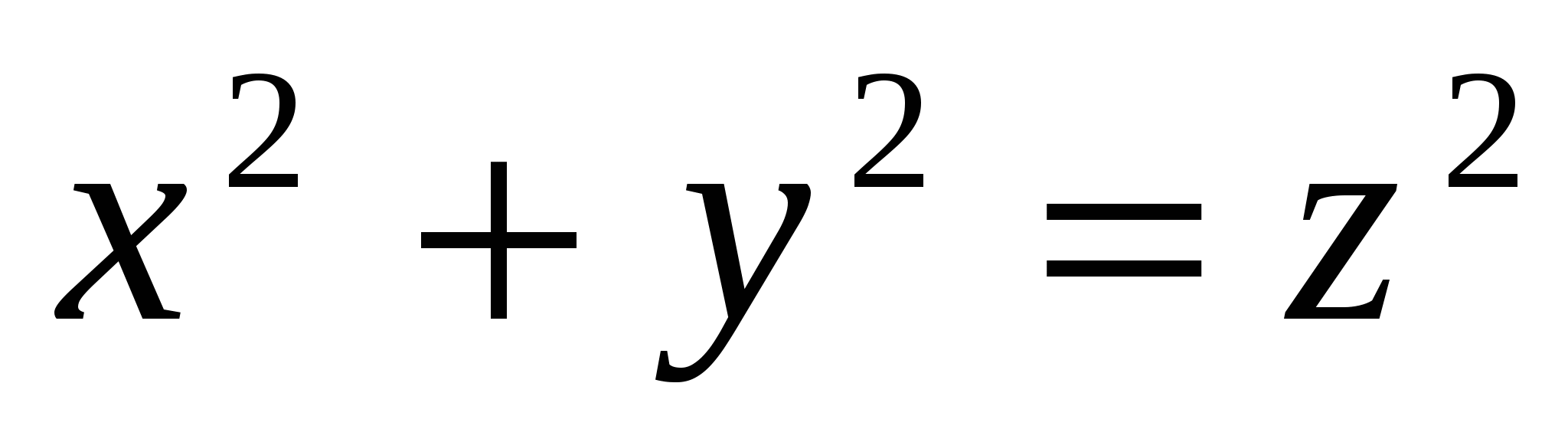 (4) в целых положительных, попарно взаимно простых числах определяются по формуле и имеют вид: (4) в целых положительных, попарно взаимно простых числах определяются по формуле и имеют вид:
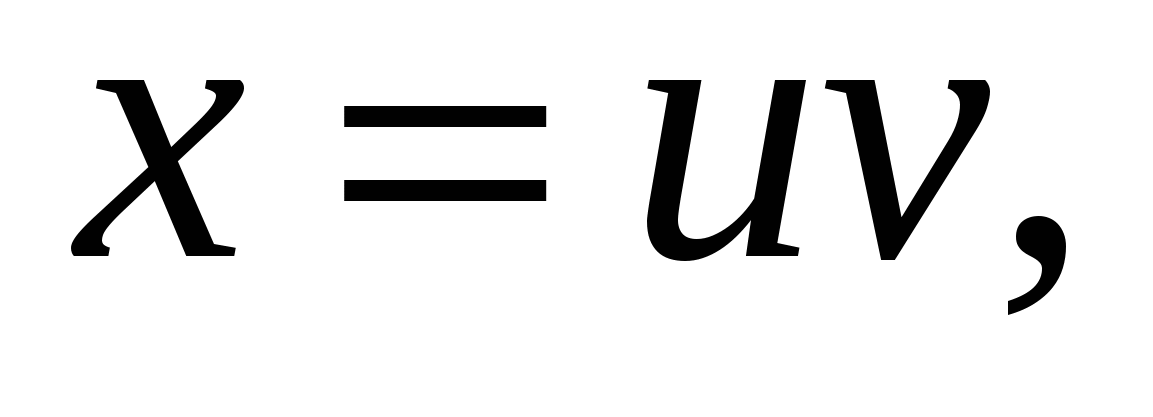 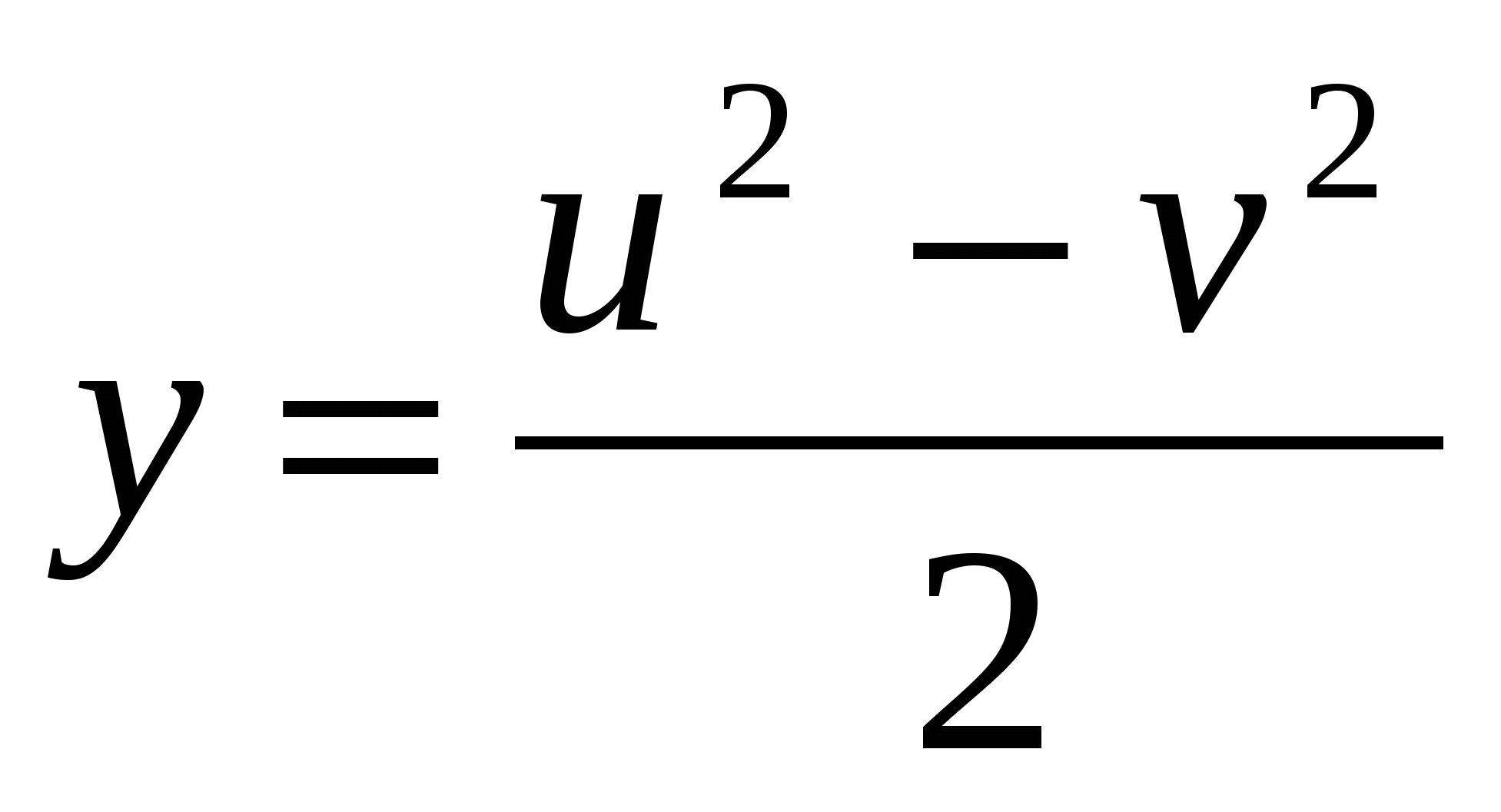 , , 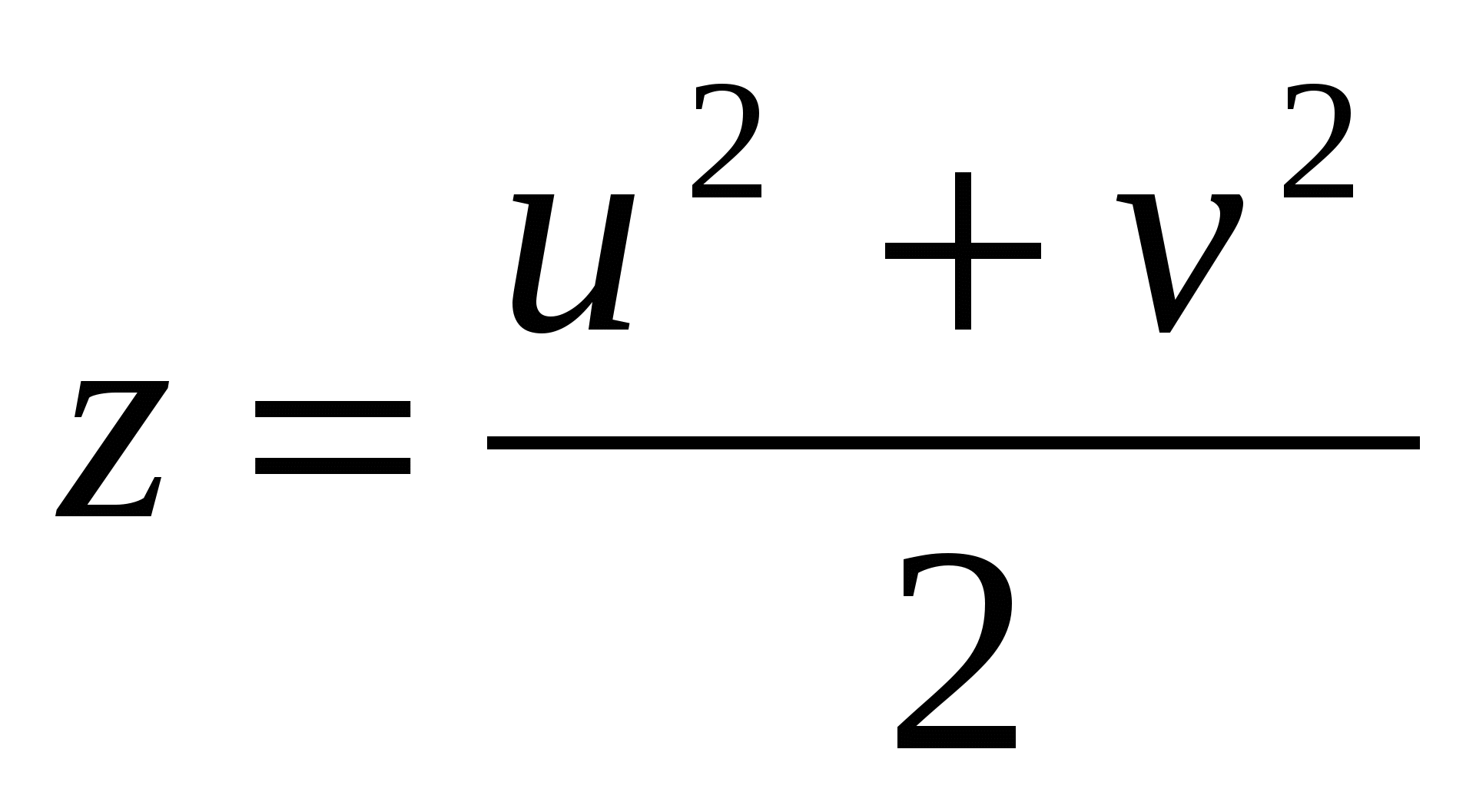 , (5) , (5)
где u и v- два любых нечетных, взаимно простых положительных числа.
Придадим несколько другой вид формулам (5), определяющим все решения уравнения (4). Так как u и v - нечетные числа, то, положив
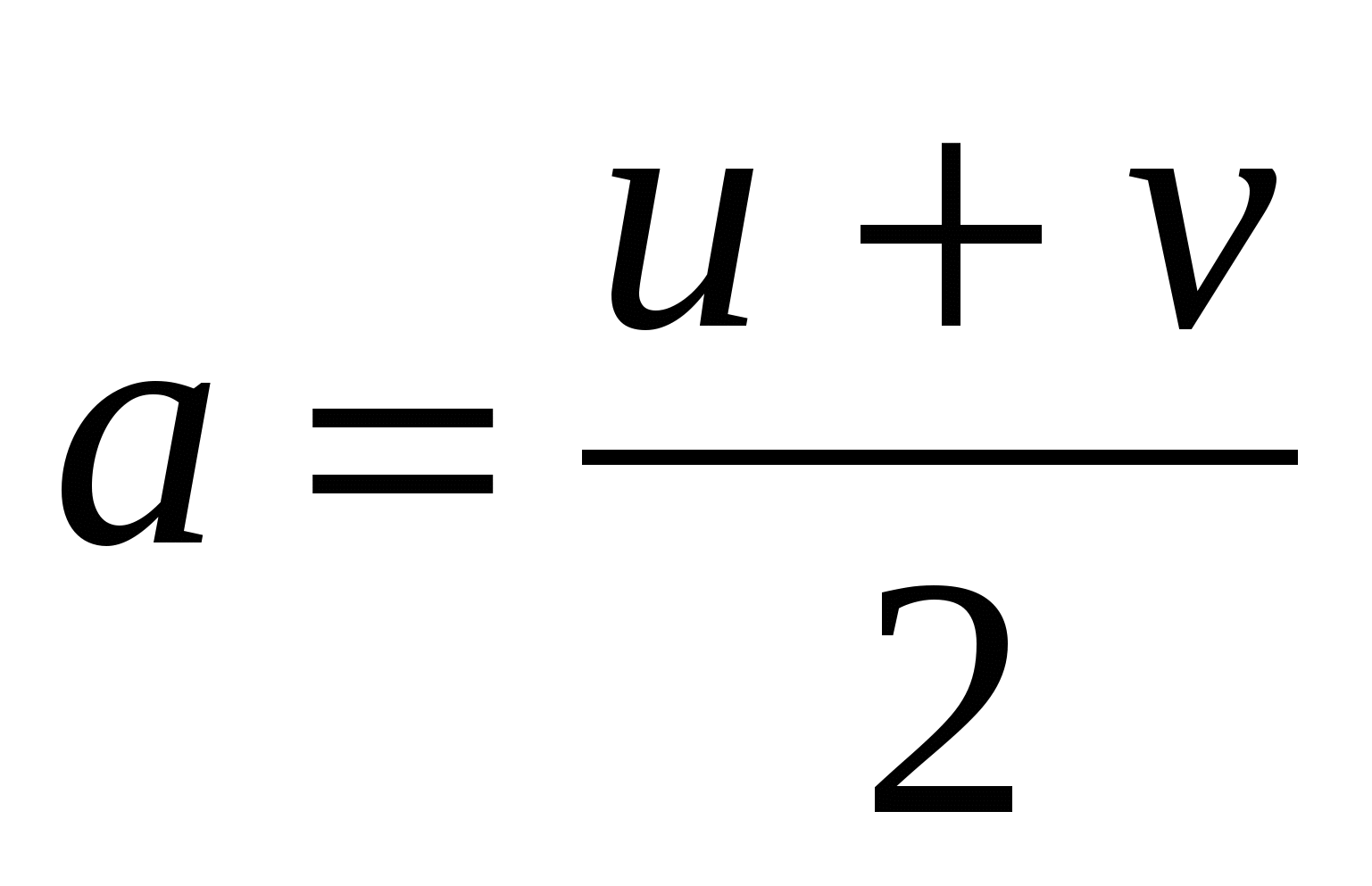 , , 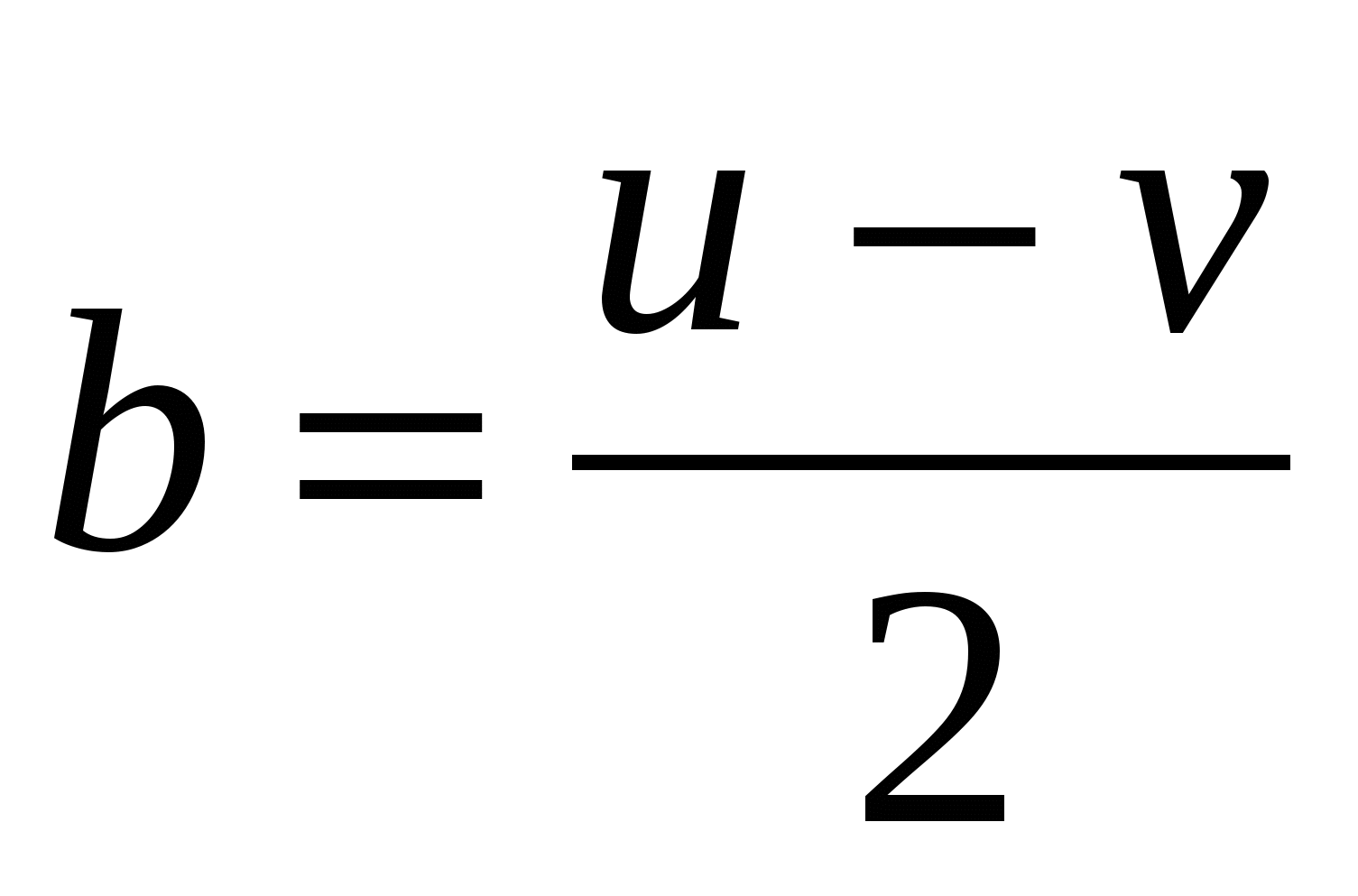 (6) (6)
мы определим числа u и v равенствами
u = a + b, v = a – b, (7)
где а и b – целые числа разной четности. Равенства (6) и (7) показывают, что любой паре нечетных взаимно простых чисел u и v соответствует пара взаимно простых чисел а и b разной четности и что любой паре взаимно простых чисел а и b разной четности соответствует пара взаимно простых нечетных чисел u и v.
Поэтому, сделав в (5) замену u и v на а и b, мы получим, что все тройки целых положительных и попарно взаимно простых чисел x,y,z (х – нечетное), являющиеся решениями уравнения (4), определяются по формулам
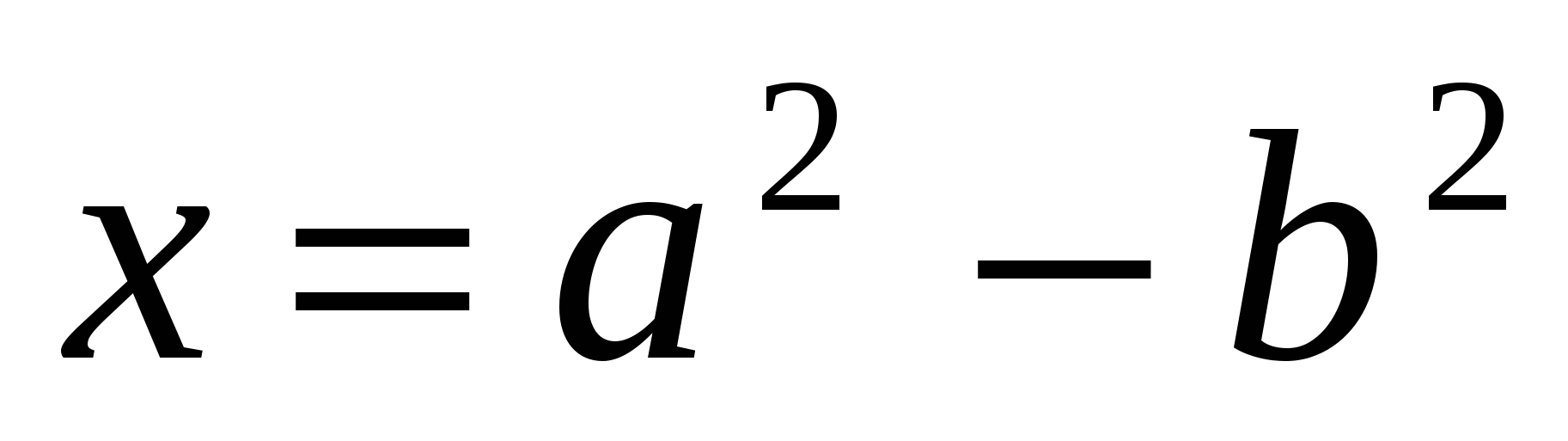 , y = 2ab, , y = 2ab, 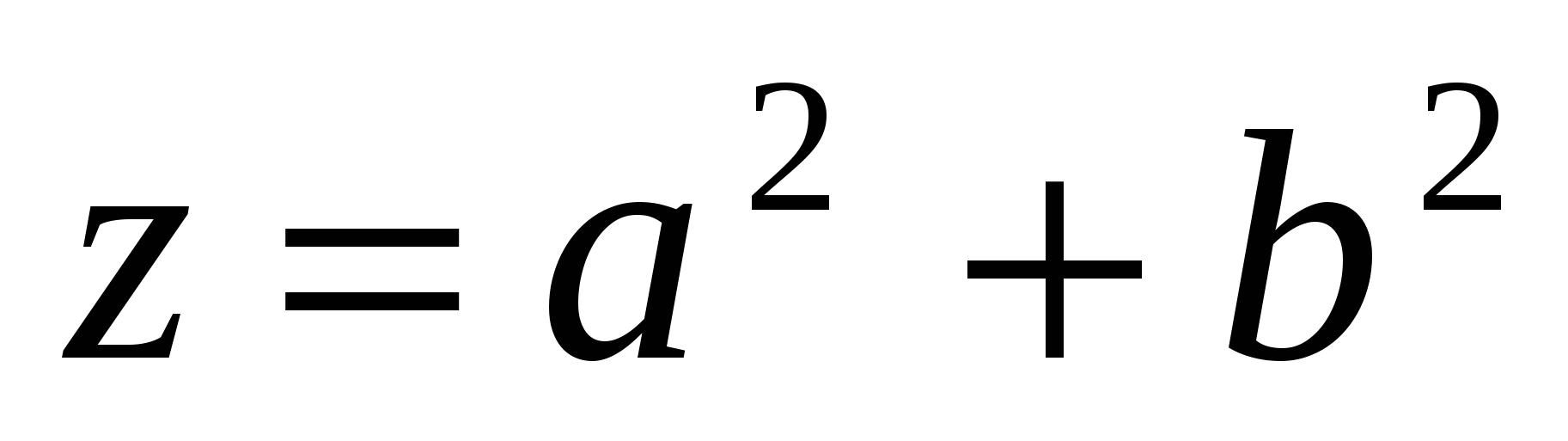 , (8) , (8)
где а и b – два любых взаимно простых числа разной четности при условии, что x>0. Эти формулы показывают, что x и y разной четности. Если уравнение (2) имеет решение [x0, y0, z0], то это значит, что
[x02]2+[y02]2 =z02,
другими словами, что тройка чисел (x02, y02 ,z0) является решением уравнение (4). Но тогда должны существовать два числа а и b, а>b, взаимно простых и разной четности, таких, что
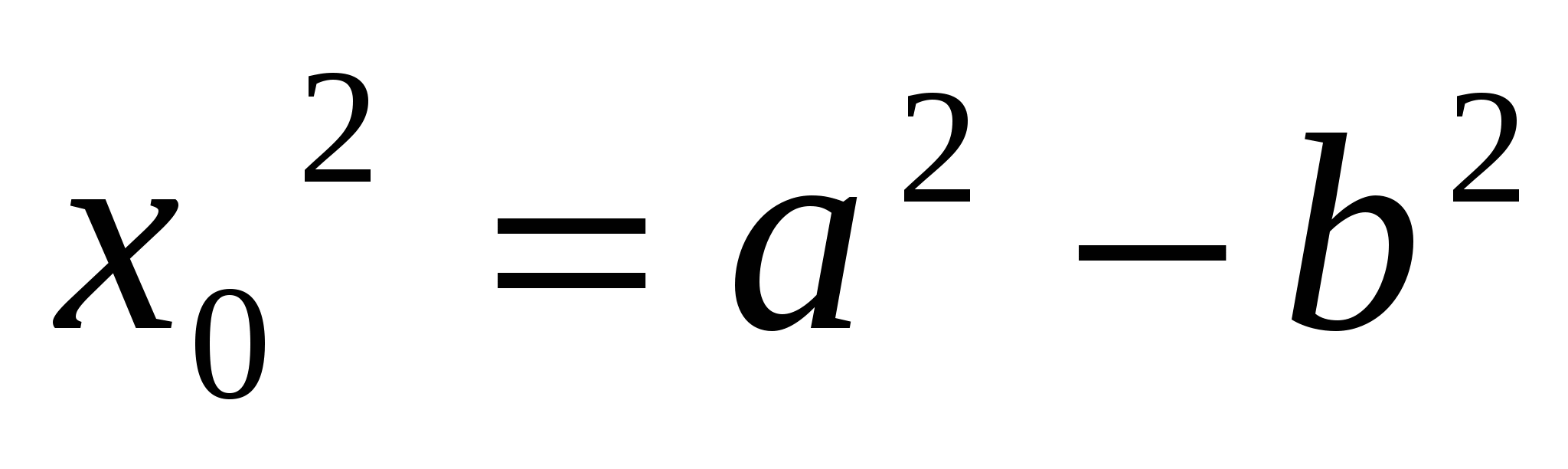 , y0 2 = 2ab, , y0 2 = 2ab, 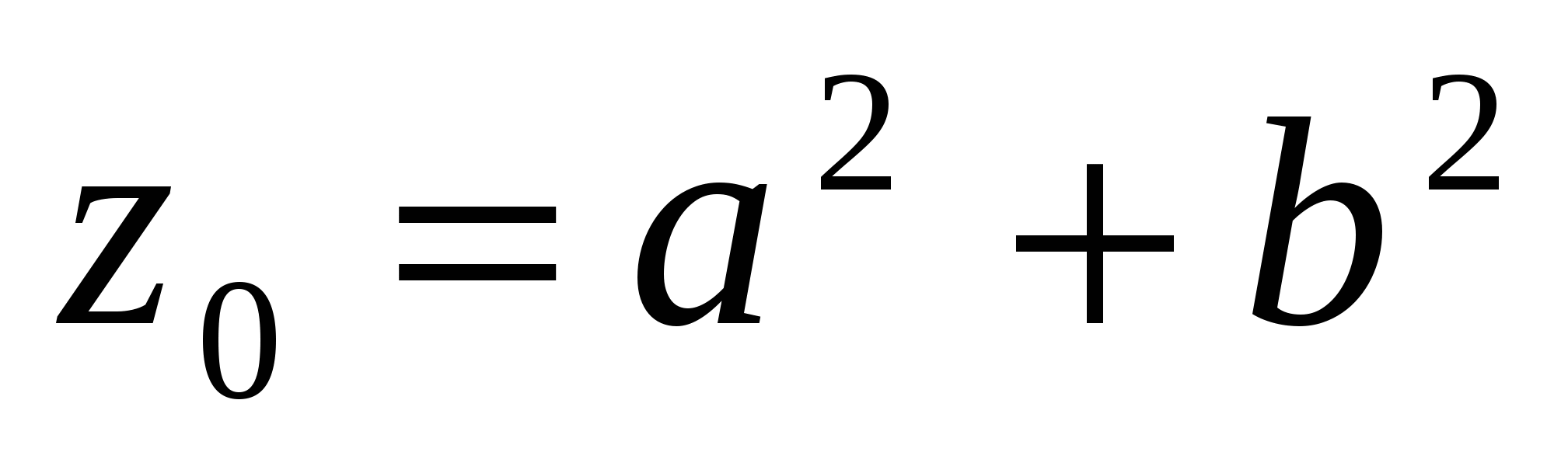 , (9) , (9)
Мы допускаем при этом, для определенности, что x0 - нечетно, y0 - четно. Противоположное допущение ничего не изменило бы, так как было бы достаточно заменить x0 на y0 и наоборот. Но мы уже знаем, что квадрат нечетного числа {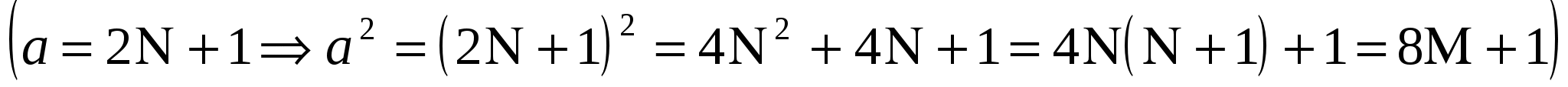 , a- всякое нечетное число, N, M - целые числа} дает в остатке 1 при делении на 4. Поэтому из равенства , a- всякое нечетное число, N, M - целые числа} дает в остатке 1 при делении на 4. Поэтому из равенства
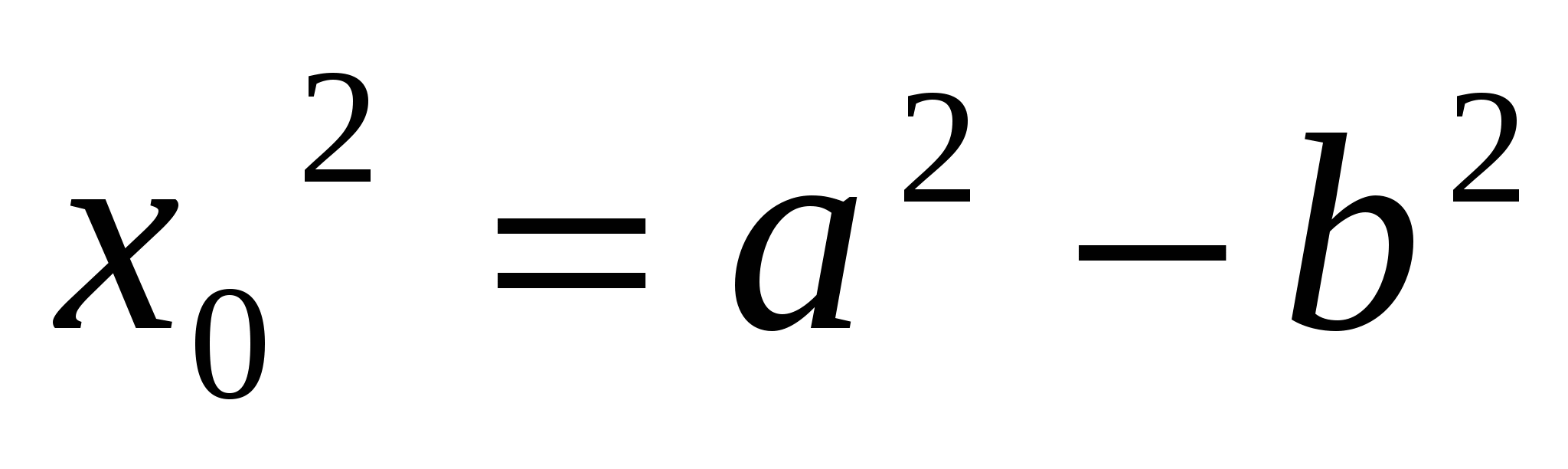 , (10) , (10)
следует, что а – нечетно, b – четно. В противном случае левая часть этого равенства при делении на 4 давала бы в остатке 1, а правая, так как мы предположили а–четным, b–нечетным, -1. Так как а–нечетно и (а,b)=1, то и (а, 2b)=1.
Но тогда из равенства
y0 2 = 2ab,
следует, что
a=t2, 2b=s2 , (11)
где t и s – какие-то целые числа. Но из соотношения (10) следует, что [x0, а, b] есть решение уравнения (4). Значит,
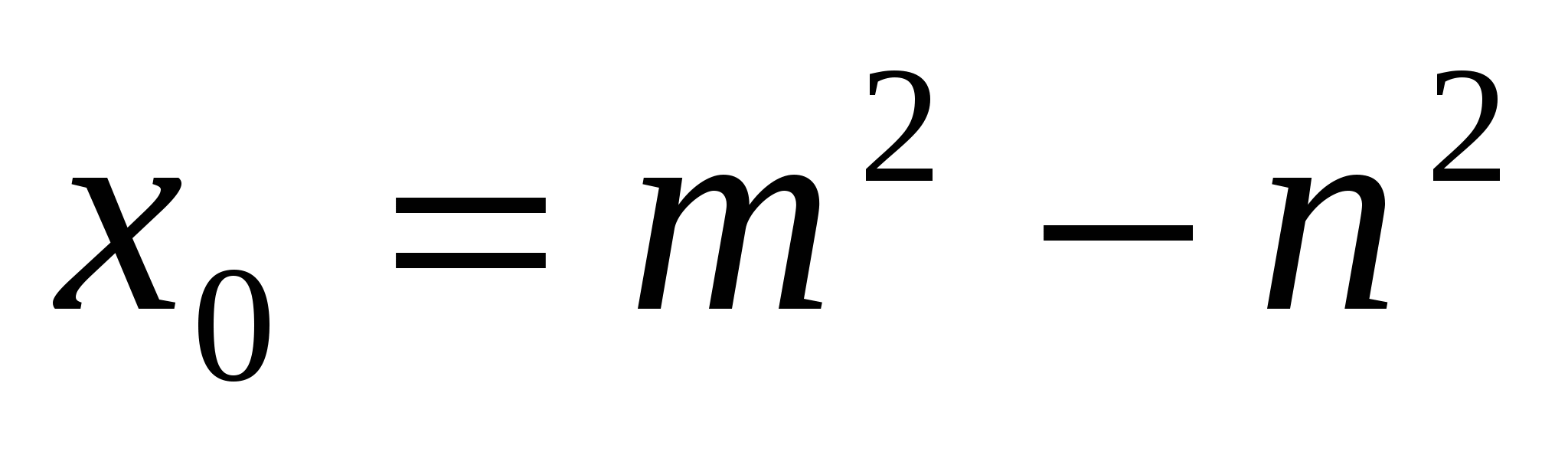 , b = 2mn, , b = 2mn, 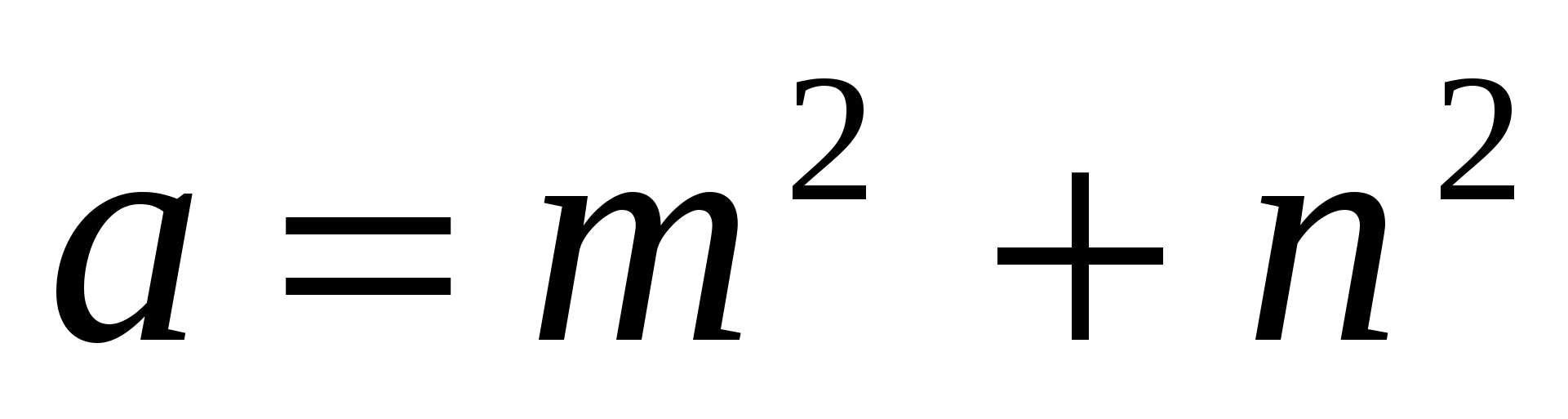 , ,
где m и n- некоторые простые числа разной четности. Из (11) имеем:
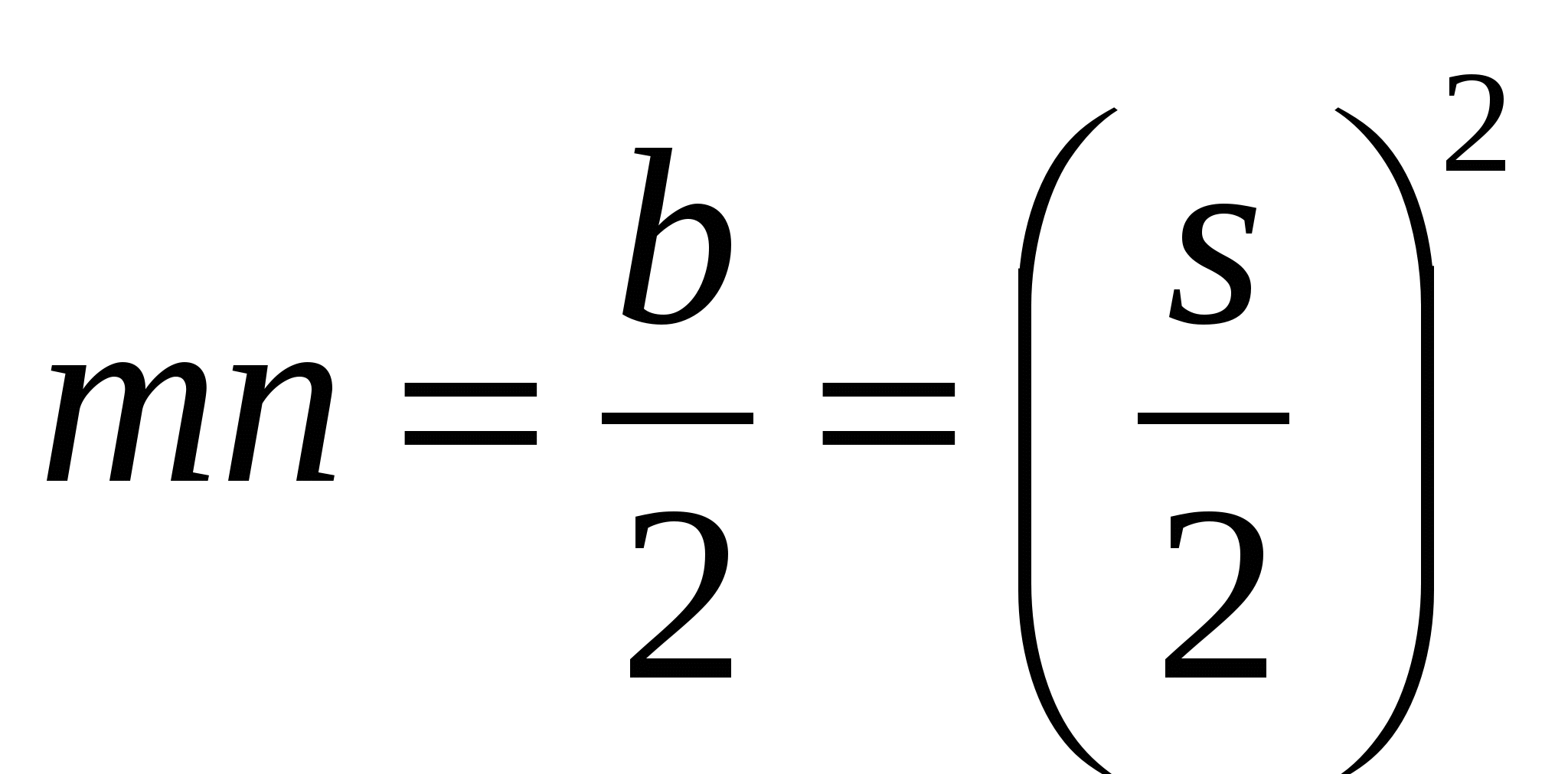 , ,
откуда в силу взаимной простоты m и n следует, что
m=p2, n=q2, (12)
где p и q-отличные от нуля целые числа. Так как 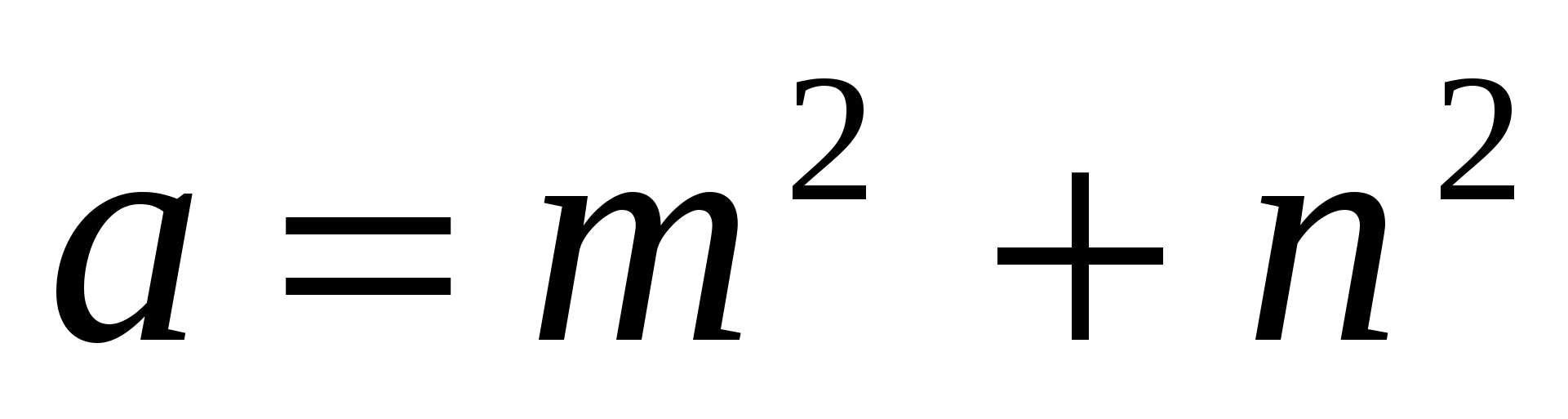 и a=t2, то и a=t2, то
q4+p4=t2, (13).
Но
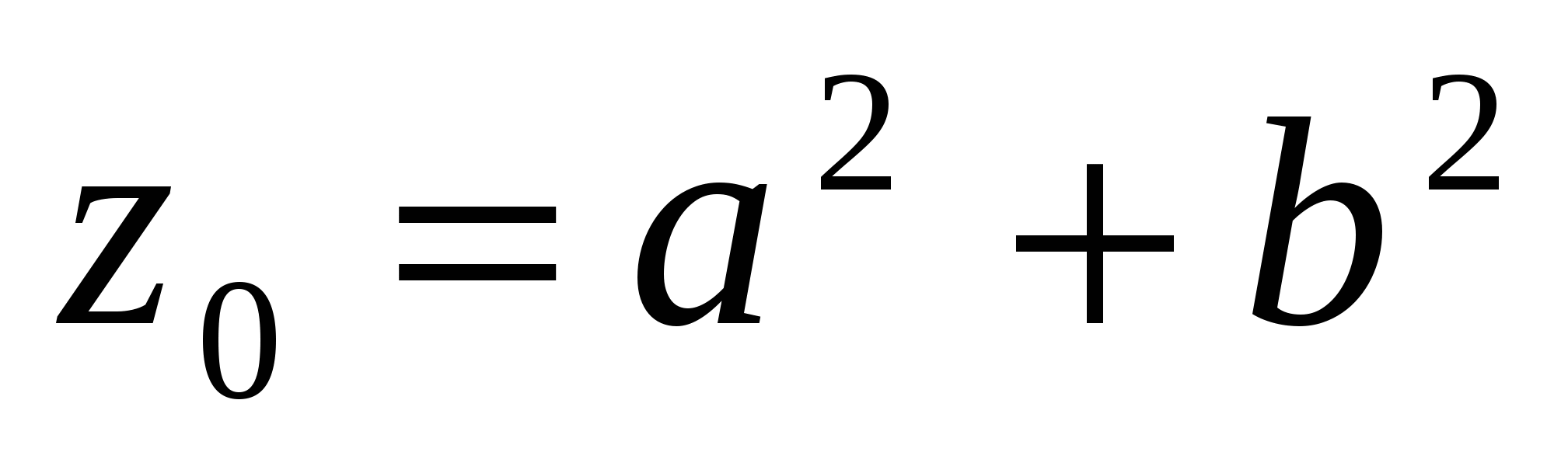 > a2. > a2. Поэтому 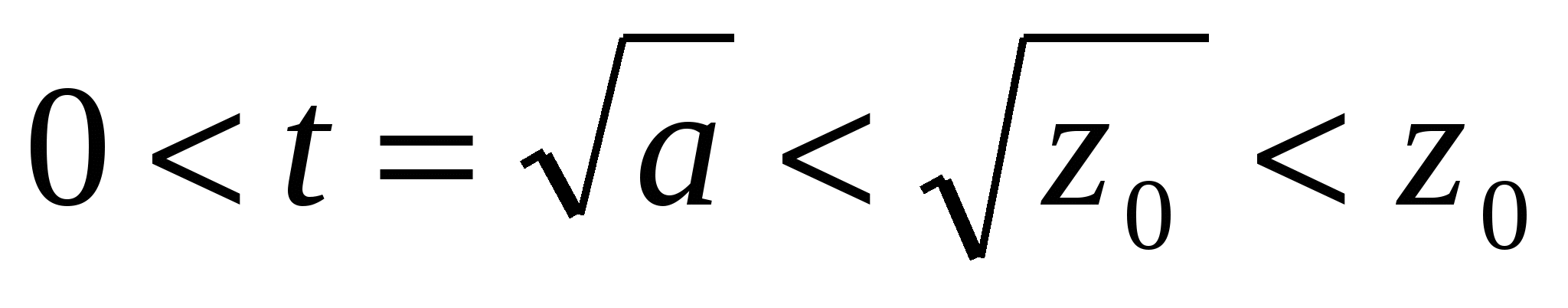 (z0>1). (14) (z0>1). (14)
Положив q=x1, p=y1, t=z1, мы видим, что если существует решение [x0,y0,z0], то должно существовать и другое решение [x1,y1,z1], причем 010. Этот процесс получения решений уравнения (2) можно получать неограниченно, и мы получим последовательность решений
[x0, y0, z0], [x1, y1, z1], …, [xn, yn, zn ], … ,
причем целые положительные числа z0, z1, z2 ,…, zn , …будут монотонно убывать; другими словами, будут верны неравенства
z0 > z1 > z2 >…> zn >…
Но целые положительные числа не могут образовать бесконечную монотонно убывающую последовательность, так как в такой последовательности не может быть больше z0 членов. Мы пришли, таким образом, к противоречию, предположив, что уравнение (2) имеет хотя бы одно решение в целых x, y, z, xyz=0. Этим доказано, что уравнение (2) не имеет решений. Следовательно, и уравнение (1) не имеет решений в целых положительных числах [x,y,z], так как в противном случае, если [x,y,z]- решение (1), то [x,y,z2]- решение (2).
Метод доказательства, которым мы пользовались, заключавшийся в построении с помощью одного решения бесчисленной последовательности решений с неограниченно убывающими положительными z, называется методом спуска. Как мы уже говорили выше, осуществить этот метод в общем случае теоремы Ферма мешает пока не единственность разложения целых чисел алгебраических колец на простые сомножители того же кольца (См.[1]).
Заметим, что мы доказали отсутствие целых решений не только у уравнения (2), но и у уравнения
x4n+y4n=z2n .
Любопытно отметить, то уравнение
x4+y2=z2
имеет бесчисленное множество решений в целых положительных числах, например x=2, y=3, z=5.
Пример. Докажем, что уравнение
x4+2y4=z2 (15)
не имеет решений в целых, отличных от нуля числах x,y,z.
Допустим, что уравнение (15) имеет решение в целых положительных числах
[x0, y0, z0]. Эти числа мы сразу можем предполагать взаимно простыми, так как если бы они имели бы НОД=d>1, то числа x0/d, y0/d, z0/d2 также были бы решением уравнения (15). Наличие общего делителя у двух из них влекло бы за собой существование общего делителя у всех трех. Кроме того, предположим, что z0 – наименьшее из всех возможных z в решениях (15) в целых положительных числах. Так как [x0,y0,z0] –решение уравнения (15), то [x02,y02,z] будут решением уравнения
x2+2y2=z2 (16)
Пользуясь формулами(1’) из §4,Пример2, дающими все целые положительные решения (16), мы видим, что существуют такие целые положительные a и b, (a,b)=1, a нечетно, которые удовлетворяют равенствам
x02 = +(a2-2b2), y02=2ab, z0=a2+2b2 (17)
Из равенства y02 =2ab следует, что b само должно быть четно, так как y четно, y делится на 4, а a нечетно. Так как (b/2,a)=1, то из равенства
(y0./2)2=a*b/2
непосредственно следует, что
a=m2, b/2=n2,
где m и n- целые положительные и (m,2n)=1. Но из (17) следует
x02=+(a2-2b2)=+[a2-8(b/2)2], (18)
где a и x0- нечетны. Мы уже видели, что квадрат нечетного числа при делении на 4 дает в остатке 1.Поэтому левая часть (18) при делении на 4 дает в остатке 1. Значит, в равенстве (18) скобка в правой части может входить только с плюсом. Теперь равенство (18) можно записать уже в форме
x02 =m4-8n4
или в форме
x02 +2(2n2)2=(m2)2, (19)
где x0, n, m-целые положительные и взаимно простые числа. Значит, числа x0, 2n2, m2 образуют решение уравнения (16), причем x0, m2, 2n2
взаимно просты. Поэтому в силу формул (1’),§4,Пример2 найдутся такие целые числа p и q, p-нечетно, (p,q)=1, что
2n2=2pq, m2=p2+2q2, x0=+(p2-2q2). (20)
Но так как (p, q)=1 и n2=pq, то p=s2, q=r2 , где s и r-целые взаимно простые числа. Отсюда окончательно следует соотношение
s4+2r4=m2 , (21)
которое показывает, что числа s, r, m образуют решение уравнения (15). Но из вышеполученных равенств
z0=a2+2b2, a=m2 .
следует, что z0 > m. Итак, имея решение [x0, y0, z0], мы нашли другое решение
[s, r, m], причем 0 < m < z0 . Это же противоречит предположению, аоторое мы сделали, что решение [x0, y0, z0] имеет другое решение z0 наименьшим из возможных. Таким образом, мы пришли к противоречию, допустив существование решения у уравнения (15), и доказали, что это уравнение неразрешимо в целых, отличных от нуля числах.
Вывод:
Более трехсот лет теорема Ферма привлекала внимание многих поколений математиков и служила беспрецедентным стимулом для развития математики. При попытках ее доказать были разработаны мощные средства, приведшие к созданию обширного раздела математики- теории алгебраических чисел. С помощью теоретико –числовой техники теорема Ферма была проверена для всех n< 4000 000. Но до конца 1994 года в общем случае оставалась недоказанной. Получить ее полное доказательство удалось лишь с помощью теории эллиптических кривых.
Литература:
Химчин А.Я. «Великая теорема Ферма»
Башмакова И.Г. «Диофант и диофантовы уравнения», М.:Наука,1972г.
Гельфонд А.О. «Решение уравнений в целых числах», М, 1957г.
Соловьев Ю.П. Гипотеза Таниямы и последняя теорема Ферма// Соросовский образовательный журнал. 1998г.№2.Стр.135-138.
Хамов Г.Г. «Элементы теории диофантовых уравнений в задачах и
упражнениях», Учебное пособие, С-П.:1986г.
Оглавление
1 Оглавление 3 Историческая справка 4 §2 Задачи, приводящие к диофантовым уравнениям. 6 Задача1. 6 Задача2. 6 Задача3. 8 Задача4. 8 §3 Методы решения диофантовых уравнений 10 Метод1. Свойства делимости и диофантовы уравнения. 10 Метод 2. Диофантовы уравнения, допускающие разложение на множители. 11 Метод 3. Метод подстановки в решении диофантовых уравнений: 12 Задание: Найти целочисленные решения следующих уравнений: 13 Метод 4. Сравнения и диофантовы уравнения. 14 Теорема1. Если удовлетворяет сравнению ax=c(b), то пара чисел (x0;(c-ax0):b) является решением (D), где (a;b)=1. 15 Теорема2: Если (a,b)=1, то (D) имеет бесконечное множество целых решений, которые находятся по формулам: 15 Следствие: (D) ax+by=c в Z либо не имеет решений, либо имеет бесконечное множество решений, которые находятся по формулам(*). 16 Указание: 16 Метод5. Метод спуска(*): 16 §4 Основные пифагоровы треугольники. 17 Задача о нахождении всех решений диофантовых уравнений второй степени. 17 17 Нет ни одной математической проблемы, которая была бы столь популярна, как знаменитая последняя теорема Ферма . 19 Это утверждение называется последней (или великой) теоремой Ферма. 20 §5 Алгебраические уравнения выше второй степени с тремя неизвестными 20 Доказательство теоремы Ферма для случая n=4 методом спуска. 22 Теорема: 22 Вывод: 26 Литература: 26 Оглавление 27
|
 Скачать 389.5 Kb.
Скачать 389.5 Kb.