|
Тестовые задания по математике за 1 полугодие для учащихся 11 класса
Тестовые задания по математике за 1 полугодие для учащихся 11 класса
1 вариант
Найдите значение выражения ![\frac{\sqrt[9]{7}\cdot \sqrt[18]{7}}{\sqrt[6]{7}}](521289_html_m556a847.png)
Найдите значение выражения 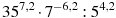
Найдите значение выражения 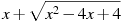 при при 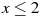
Найдите точку минимума функции 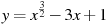
Найдите наименьшее значение функции 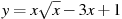 на отрезке на отрезке ![[1;9]](521289_html_35e751f7.png)
Решите уравнение 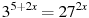
Решите уравнение 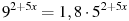
Решите неравенство  . В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
Найдите значение выражения 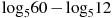
Найдите значение выражения 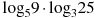
Найдите корень уравнения 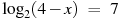
Решите уравнение 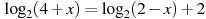
Решите уравнение 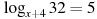 . Если уравнение имеет более одного корня, в ответе укажите меньший из них. . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Найдите значение выражения 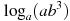 , если , если 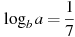 . .
Решите неравенство  . В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
2 вариант
Найдите значение выражения ![\frac{\sqrt[15]{6}\cdot \sqrt[10]{6}}{\sqrt [6]{6}}](521289_html_m14b122eb.png)
Найдите значение выражения 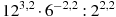
Найдите значение выражения 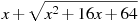 при при 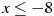
Найдите точку минимума функции 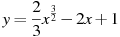
Найдите наименьшее значение функции 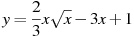 на отрезке на отрезке ![[1;9]](521289_html_35e751f7.png)
Решите уравнение 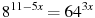
Решите уравнение 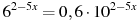
Решите неравенство  . В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
Найдите значение выражения 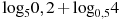
Найдите значение выражения 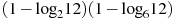
Найдите корень уравнения 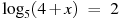 . .
Решите уравнение 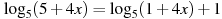
Решите уравнение 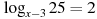 . Если уравнение имеет более одного корня, в ответе укажите меньший из них. . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Найдите 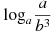 , если , если 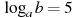 . .
15. Решите неравенство 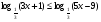 . В ответе укажите наибольшее целое решение. . В ответе укажите наибольшее целое решение.
3 вариант
Найдите значение выражения ![\frac{\sqrt[24]{10}\cdot \sqrt[12]{10}}{\sqrt [8]{10}}](521289_html_5b304862.png)
Найдите значение выражения 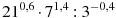
Найдите значение выражения 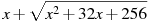 при при 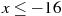
Найдите точку максимума функции 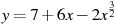
Найдите наибольшее значение функции 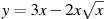 на отрезке на отрезке ![[0;4]](521289_html_m1c4e5278.png)
Решите уравнение 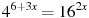
Решите уравнение 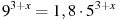
Решите неравенство 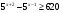 . В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
Найдите значение выражения 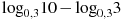
Найдите значение выражения ![{{\log }_{\sqrt[6]{13}}}13](521289_html_m3e0089aa.png)
Найдите корень уравнения 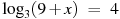
Решите уравнение 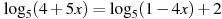
Решите уравнение 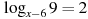 . Если уравнение имеет более одного корня, в ответе укажите меньший из них. . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Найдите 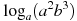 , если , если 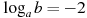 . .
Решите неравенство 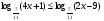 . В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
4 вариант
Найдите значение выражения ![\frac{\sqrt[20]{10}\cdot \sqrt[5]{10}}{\sqrt [4]{10}}](521289_html_2a64d8c5.png)
Найдите значение выражения 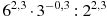
Найдите значение выражения 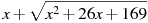 при при 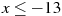
Найдите точку максимума функции 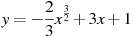
Найдите наибольшее значение функции 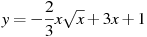 на отрезке на отрезке ![[1;9]](521289_html_35e751f7.png)
Решите уравнение 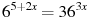
Решите уравнение 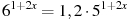
Решите неравенство 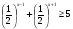 . В ответе укажите наибольшее целое решение. . В ответе укажите наибольшее целое решение.
Найдите значение выражения 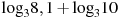
Найдите значение выражения 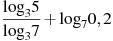
Найдите корень уравнения 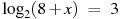
Решите уравнение 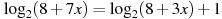
Решите уравнение 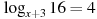 . Если уравнение имеет более одного корня, в ответе укажите меньший из них. . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
Вычислите значение выражения 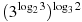 . .
Решите неравенство  . В ответе укажите наибольшее целое решение. . В ответе укажите наибольшее целое решение.
Ответы
Вариант/ задания
|
1 вариант
|
2 вариант
|
3 вариант
|
4 вариант
|
|
1
|
1
|
1
|
1
|
|
875
|
12
|
147
|
9
|
|
2
|
-8
|
-16
|
-13
|
|
4
|
4
|
4
|
9
|
|
-3
|
-8
|
1
|
10
|
|
1,25
|
1
|
6
|
1,25
|
|
-0,2
|
0,2
|
-2
|
0
|
|
-1
|
-3
|
2
|
-1
|
|
5
|
-3
|
-1
|
4
|
|
4
|
1
|
6
|
0
|
|
-124
|
21
|
72
|
0
|
|
0,8
|
0
|
0,2
|
8
|
|
-2
|
8
|
9
|
-1
|
|
22
|
-14
|
-4
|
3
|
|
4
|
5
|
5
|
4
|
При проверке за каждое из заданий выставляется 1 балл, если ответ правильный, и 0 баллов, если ответ неправильный.
Максимальное количество баллов: 15.
Нормы выставления оценок
Баллы
|
0-8
|
9-11
|
12-13
|
14-15
|
Оценка
|
«2»
|
«3»
|
«4»
|
«5»
| |
|
|
 Скачать 54.41 Kb.
Скачать 54.41 Kb.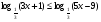 . В ответе укажите наибольшее целое решение.
. В ответе укажите наибольшее целое решение. . В ответе укажите наименьшее целое решение.
. В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
. В ответе укажите наименьшее целое решение. . В ответе укажите наименьшее целое решение.
. В ответе укажите наименьшее целое решение.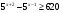 . В ответе укажите наименьшее целое решение.
. В ответе укажите наименьшее целое решение.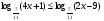 . В ответе укажите наименьшее целое решение.
. В ответе укажите наименьшее целое решение.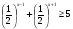 . В ответе укажите наибольшее целое решение.
. В ответе укажите наибольшее целое решение. . В ответе укажите наибольшее целое решение.
. В ответе укажите наибольшее целое решение.