Курсовая работа по теме: «Некоторые диофантовы уравнения»
 Скачать 389.5 Kb. Скачать 389.5 Kb.
|
Метод 4. Сравнения и диофантовы уравнения.Применим свойства сравнений к решению некоторых уравнений. Многие уравнения, решаемые с помощью свойств делимости, могут быть решены при помощи сравнений. Неопределенные уравнения с двумя неизвестными: (D): ax+by=c , x,y[-Z ,a,b,c[-Z Найти решения уравнения , то есть значения x,y[-Z. (a;b)=d
ax+by=c:d a=a1d , b=b1d , c=c1d. a1x+b1y=c1 следовательно (a1;b1)=1. Таким образом, пришли к выводу, что (a;b)=1. Теорема1. Если удовлетворяет сравнению ax=c(b), то пара чисел (x0;(c-ax0):b) является решением (D), где (a;b)=1.Док-во: ax0=c(b)- верное числовое сравнение, следовательно, разность чисел (c-ax0)/b[по определению сравнимых чисел], значит, (c-ax0):b-целое число. Подставим вместо x----x0, y----(c-ax0)/b. Если в результате получим c ,то все доказано. Подставляем: ax0+b(c-ax0)/b=ax0+c-ax0=c; В самом деле, пара (x0;(c-ax0)/b)-решение(D). Теорема2: Если (a,b)=1, то (D) имеет бесконечное множество целых решений, которые находятся по формулам: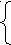 (*) x=x0-bt, y=y0+at; t[-Z (x0;y0)- некоторое решение (D) Док-во: 1) Покажем, что (x;y)- по формуле (*) решение (D). a(x0-bt)+b(y0+at)=ax0-abt+by0+bat=c, так как[x0,y0]-решение(D). 2) Покажем, что любое решение (D) находится по этим формулам(*); (x0;y0)-некоторое решение (D). Так как (x0;y0)-решение(D) и пара (x;y) тоже берется как решение, тогда: а)ax0+by0=c, б)ax+by=c-верное числовое равенство; Вычтем из а)-б): a(x0-x)+b(y0-y)=0<->a(x0-x)=b(y-y0),так как a(x0-x):b, x0-x:b, b(y-y0):a,[так как (a;b)=1], то y-y0:a; По определению делимости следует, что существует t[-Z , такое что x-x0=bt, y-y0=at; 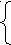 Значит, (*) x=x0-bt Значит, (*) x=x0-bty=y0+at ч.т.д. Следствие: (D) ax+by=c в Z либо не имеет решений, либо имеет бесконечное множество решений, которые находятся по формулам(*).Пример1: Найти все целые решения: 50x-42y=34/:2 (1) 25x-21y=17 (2) (1)<->(2) (25,21)=1, (1) имеет бесконечное множество решений. x=x0+21t, y=y0+25t, t[-Z Найдем x0,y0. Уравнение (2) можно свести к сравнению первой степени: 25x=17(21) 4x= -4(21) /:4, так как (4;21)=1; Имеем: x= -1(21), то есть x=20(21); Значит, x0=20 21y=25x-17 <-> y=(25*20-17):21=23, y0=23 Решение: x=20+21t, y=23+25t; t[-Z Вместо 20 можно было взять -1 Указание:Школьники решают (D) методом спуска. Систематическое изучение диофантовых уравнений в средней школе способствует привитию навыков самостоятельной работы в математике и играет большую роль в повышении уровня математической подготовки школьников. Пример2: 3x+4y=13 (*) Аналогично предыдущему примеру1 , из уравнения имеем: 3x=1(4). Откуда x=3(4) , то есть x=3+4t, t[-Z. Подставляя в уравнение, найдем y=1-3t. Множество решений: {(3+4t,1-3t);t[-Z}. Метод5. Метод спуска(*):Пример3: 5x3+11y3+13z3=0. Имеем сравнение: 5x3+11y3=0(13). Так как a3=0;1;5;8;12(13), то число 5x3+11y3делится на 13 тогда и только тогда, когда x=y=0(13). Поэтому x=13x1, y=13y1,z=13z1 . Подставив в уравнение, получим: 5x13+11y13+13z13=0. Продолжая этот процесс, получим, что числа x,y,z делятся на любую натуральную степень числа 13. Это возможно лишь при условии, когда x=y=z=0. §4 Основные пифагоровы треугольники. Задача о нахождении всех решений диофантовых уравнений второй степени. Пример1.(**) Рассмотрим уравнение второй степени с тремя неизвестными: X2+Y2=Z2 (1) Геометрически решение этого уравнения в целых числах можно использовать как нахождение всех пифагоровых треугольников, то есть прямоугольных треугольников, у которых катеты x,y и гипотенуза z выражаются целыми числами. Обозначим через d=НОД(x,y). Тогда x=x1d, y=y1d и уравнение(1) примет вид: x12d2+y12d2=z2. Отсюда следует, что z2 : на d2 и, значит, z кратно d: z=z1d .Теперь уравнение (1) можно записать в виде: x12d2+y12d2=z12d2; сокращая на d2 , получим: x12+y12=z12 . Мы пришли к уравнению того же вида, что и исходное, причем теперь величины x1 и y1 не имеют общих делителей, кроме 1.Таким образом, при решении уравнения (1) можно ограничиться случаем, когда x и y взаимно просты. Итак, пусть(x;y)=1. Тогда хотя бы одна из величин x и y (например, x будет нечетной). Перенося y2 в правую часть уравнения (1) получим: x2=z2-y2; x2=(z-y)(z+y) (2). Обозначим через d1 НОД выражений z+y и z-y. Тогда z+x=ad1 , z-y=bd1 , (3) , где (a,b)=1. Подставляя во (2) значения z+y и z-y , получим: x2=abd12. Так как числа a и b не имеют общих делителей, то полученное равенство возможно только в том случае, когда a и b будут полными квадратами(**) : a=U2 ; b=V2 . Но тогда x2=U2V2d12; x=UVd1 (4). Найдем теперь y и z из равенств(3). Сложение этих равенств дает: 2z=ad1+bd1=U2d1+V2d1 ; z=d1(U2+V2):2 (5) Вычитая второе из равенств (3) из первого, получим: 2y=ad1-bd1=U2d1-V2d1 ; y=d1(U2-V2):2 (6) . В силу нечетности x из (4) получаем, что U,V и d1 также нечетны. Более того, d1=1, так как иначе из равенств x=UVd1 и y=d1(U-V):2 следовало бы, что величины x и y имеют общий делитель d1=1,что противоречит предположению об их взаимной простоте. Числа U и V связаны со взаимно простыми числами a и b равенствами: a=U2, b=V2 и в силу этого сами взаимно просты: V x=UV; y=(U2-V2):2; z=(U2+V2):2, (7), дающие возможность при нечетных взаимнопростых U и V(V x,y,z, удовлетворяющие уравнению (1). Простой подстановкой x,y,z в уравнение(1) легко проверить, что при любых U и V числа (7) удовлетворяют этому уравнению. Для начальных значений и формулы (7) приводят к следующим часто встречающимся равенствам: 32+42=52 (V=1;U=3), 52+122=132 (V=1;U=5), 152+82=172(V=3;U=5), Как уже было сказано, формулы (7) дают только те решения уравнения x2+y2=z2 в которых числа x, y и z не имеют общих делителей. Все остальные целые положительные решения этого уравнения получаются домножением решений, содержащихся в формулах (7), на произвольный общий множитель d. Тем же путем, каким мы получили все решения уравнения (1), могут быть получены и все решения других уравнений того же типа. Пример2: Найдем все решения уравнения (1): x2+2y2=z2 в целых положительных, попарно простых числах x, y, z. Заметим, что если x, y, z есть решения уравнения (1) и x, y, z не имеют общего делителя, отличного от 1,то они и попарно взаимно просты. Действительно, если x и y кратны простому числу p>2, то из равенства следует, так как его левая часть – целое число, что z кратно p. То же самое будет, если x и y или y и z делятся на p. Заметим, что х должно быть числом нечетным для того, что НОД(x,y,z)=1. Действительно, если х четно, то левая часть уравнения (1) будет четным числом и, значит, z также будет четным. Но x2 и z2 будут тогда кратны 4. Отсюда следует, что 2y2 должно делиться на 4, другими словами, что y тоже должно быть четным числом. Значит, если х четно, то все числа x, y, z должны быть четными. Итак, в решении без общего, отличного от 1 делителя х должно быть нечетным. Отсюда уже следует, что и z должно быть тоже нечетным. Перенося x2 в правую часть, получаем: 2y2 =z2-x2=(z+x)(z-x); Но НОД(z+x;z-x)=2. Действительно, пусть НОД(z+x;z-x)=d. Тогда z+x=kd, z-x=ld, где k,l [ -Z. Складывая и вычитая эти равенства, будем иметь: 2z=d(k+l), 2x=d(k-l). Но z и x нечетны и НОД(z;x)=1. Поэтому НОД(2x;2z)=2. Отсюда следует, что d=2. Итак, или z+x и В первом случае из равенства (z+x) 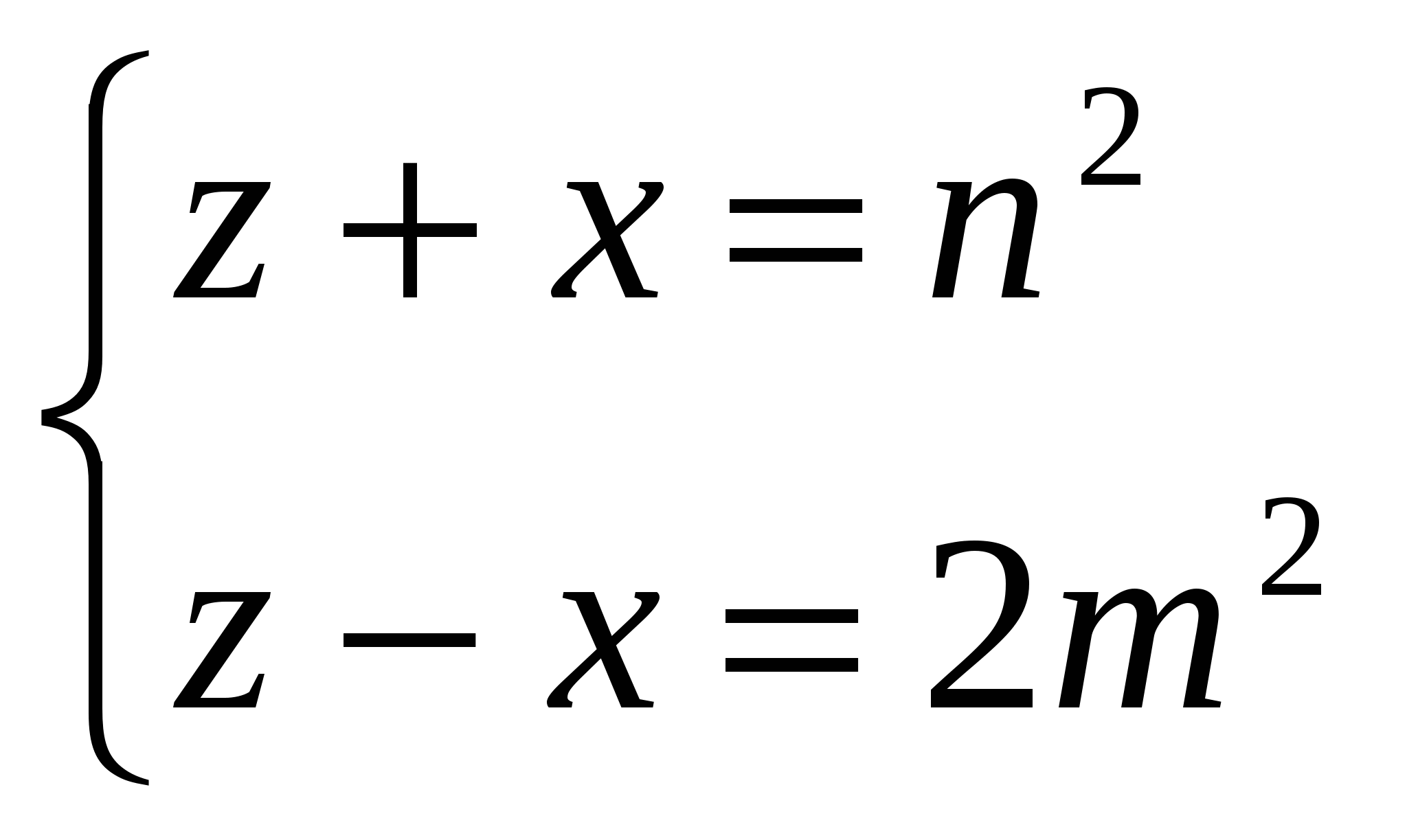 , а во втором случае из равенства , а во втором случае из равенства 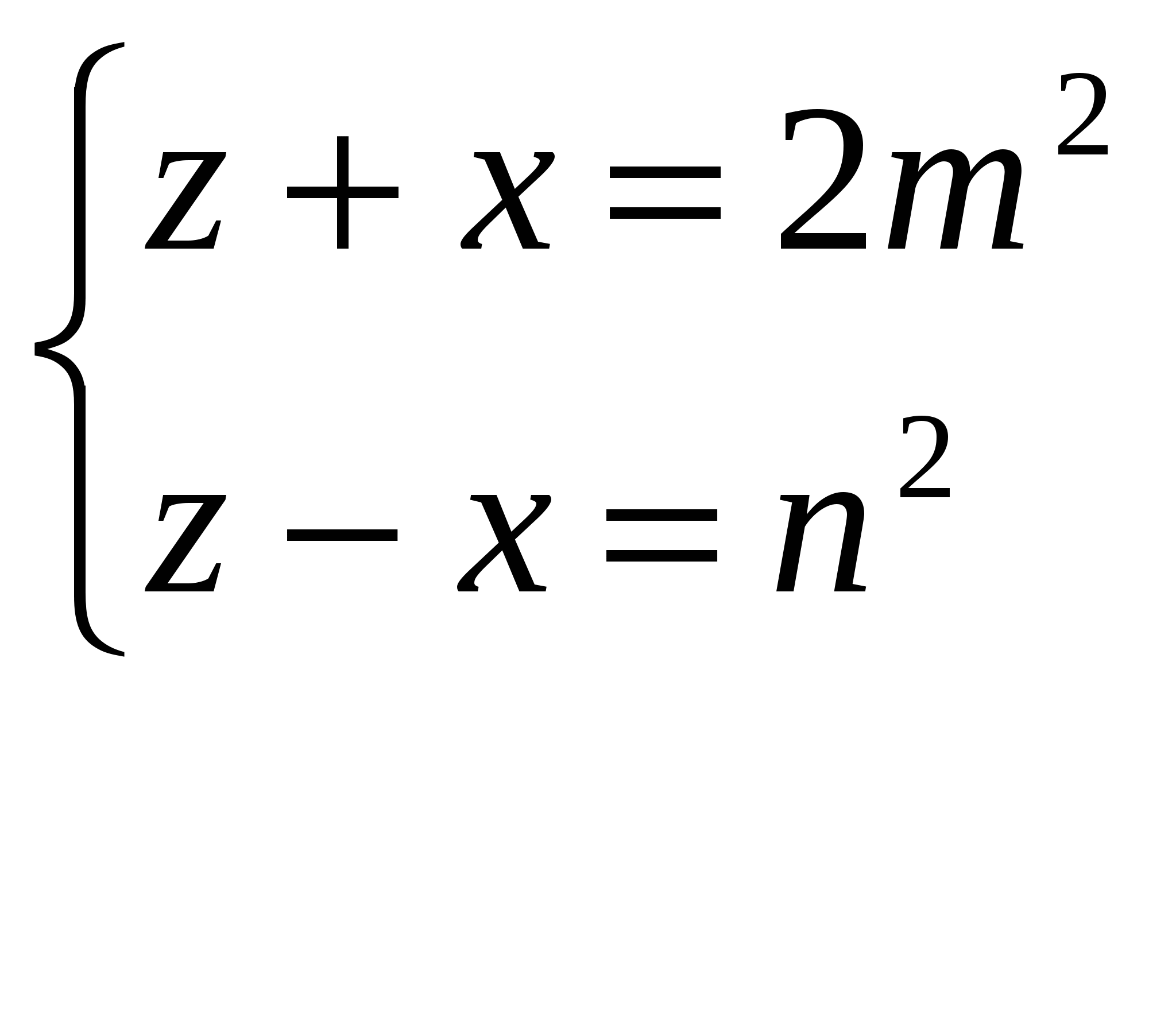 , где n, m [-Z; m – нечетное число; n,m>0. , где n, m [-Z; m – нечетное число; n,m>0.Решая эти две системы уравнений относительно x и z и находя y, мы получаем: или или Объединяя эти две формы представления решения x, y, z, мы получаем общую формулу: Но, для того, чтобы z, x [-Z, необходимо, чтобы n было четным. Полагая n=2b, m=a, мы получим окончательно общие формулы, дающие все решения уравнения (1) в целых положительных, без общего делителя, большего 1, числах x, y, z: (1/) При этих условиях величины а и b выбираются произвольно, но так, чтобы х>0. Формулы (1) действительно дают все решения в целых положительных и взаимно простых числах x, y, z, так как, с одной стороны, доказано, что x, y, z в этом случае должны представляться по формулам (1/), а с другой стороны, если задать числа a и b, удовлетворяющие условиям, то x,y,z будут действительно взаимно просты и будут решением уравнения (1). |