Курсовая работа по теме: «Некоторые диофантовы уравнения»
 Скачать 389.5 Kb.
|
Задание: Найти целочисленные решения следующих уравнений:11) x2+y2=x+y, a=1,b=0,c=1,d=-1,e=-1 Решение: Применим подстановку y=tx , получим : x=-(-1-t):(1+t2)=(1+t):(1+t2); y=-t(-1-t):(1+t2)=2t:(1+t2); ,t[-Q При t=m:n; m,n[-Z,n>0, x=(1+t):(1+t2)=(n2+mn):(n2+m2). Полученная дробь при n>1,m=n не является целым числом. Целые решения при t=-1;0;1;(0;0);(1;0);(1;1) ,а также (0;1). 12) y2=x2+x+2; Решение: Применим первую подстановку Эйлера:y=x+m. Тогда x=(2-m2):(2m-1)=-1/2(m+(m-4):(2m-1)) . Ясно, что при m<=-4 и m=>5 имеем 0<(m-4):(2m-1)<1, поэтому число x может быть целым лишь при m=-3;-2;-1;0;1;2;3;4. Множество решений уравнения: {(1;-2);(-2;-2);(1;2);(-2;2)} 13) 2x2-5x+16-y2=0<->y2=2x2-5x+16. Решение: Применим вторую подстановку Эйлера : y=4+tx. Полагая t=m:n; m,n[-Z. НОД(m;n)=1,n>0, получим, что x делится на n и x=(8t+5):(2-t2)=(8m+5n):(2n2-m Целыми решениями уравнения будут, например, при n=1: (13;17);(-3;7);(0;4);(0;-4);(13;-17);(-3;-7); n=2: (-68;-98);(-3;7) и т.д. 14) y=3x+2x+5. Решение: применяем третью подстановку Эйлера: y=(x-1), t[-Q. Тогда x=(t2+5):(t2-3)=1+8:(t2-3); y=8t:(t2-3) При целых значениях t имеем (t3-3):8, что возможно при t=1;-1;2;1;-2 и получаем решения: (1;0);(-3;4);(-3;-4);(9;16);(9;-16). Полагая t=m/n; m,n[-Z, n>0, получим: x=1+8n:(m-3n); y=8mn:(m-3n) Целые решения возможны, если -4n кроме найденных ранее решений , получим: (-35;-60);(-35;60) ит.д. 15) y2=2x3-2x2-10x-6<->y2=2(x+1)2(x-3). Решение: Полагая y=t(x+1), получим x=(t2+6):2; y=t(t2+8):2, t[-Z. Числа x,y-целые, если t=2k,k[-Z Тогда 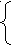 x=2k2+3y=4k(k2+2), k[-Z Множество решений: {(-1;0),(2k2+3;4k(k2+2),k[-Z} 16) xy=yx ,x,y[-N,x=y Пусть y>x. Полагаем y=(1+t)x, t[-N .Тогда x(1+t)x=yx<->x1+t=y. Отсюда x1+t=(1+t)x, или xt=1+t. Таким образом, x=(1+t)1/t y=(1+t)(1+t)1/t . Так как число x натуральное, то 1+t=mt ,m[-N . Отсюда имеем t=mt-1=(m-1)(mt-1+mt-2+...+1). При t>1: m>1 и, следовательно, mt-1+mt-2+...+m+1>t. При t=1: m=2. Множество решений: {(2;4);(4;2)}
Решение: Из уравнения следует: 5x-1<5 и 5y-1<5, то есть 1<x<5 и 1<y<5. Множество решений: {(1;2);(2;1).
Решение: Для целого числа k, k=1: 1/k<1/2. Ни одно из чисел x,y,z не может быть отрицательным, так как, например, при x<0: 1/x+1/y+1/z<0+1/2+1/2=1. Найдем решения, для которых 1<x<y<z. Другие решения получаются перестановкой. Итак, 1>1/x>1/y>1/z. Ясно, что x<3, так как при x>3 имеем: 1/x+1/y+1/z<1/3+1/3+1/3=1. Поэтому возможны 2 случая: x=3,тогда y=z=3, и x=2, тогда 1/y+1/z=1/2. Здесь y<4, так как при y>4:1/y+1/z<1/4+1/4=1/2.Получаем два решения: y=4, z=4, y=3, z=6. Множество решений: {(3;3;3),(2;3;6),(3;6;2),(6;2;3),(3;2;6),(2;6;3),(6;3;2),(2;4;4),(4;2;4),(4;4;2)} |