|
§ 5. Учебный план темы «Квадратные уравнения»
Тема «Квадратные уравнения» разбита на 11 часов:
1. Определение квадратного уравнения. Неполные квадратные уравнения (2 ч.).
Знать: определение квадратного уравнения; неполного квадратного уравнения, приведенного.
Уметь решать неполные квадратные уравнения.
2.Формула корней квадратного уравнения (3 ч.).
Знать определение дискриминанта, формулы дискриминанта и корней
Уметь выделять квадрат двучлена, решать квадратное уравнение по этим формулам; определять количество корней.
3. Самостоятельная работа (1 ч.).
4. Решение задач с помощью квадратных уравнений (2 ч.).
Уметь решать задачи с помощью квадратных уравнений.
5. Теорема Виета (2ч.).
Знать теорему Виета и обратную ей (доказательство); формулы для решения уравнения по т. Виета.
Уметь находить корни по т. Виета и коэффициенты по уже известным корням уравнения.
6. Контрольная работа: «Квадратные уравнения» (1ч.) (Приложение 2)
В тематическом планировании отражено многообразие видов деятельности учащихся, чтобы помогать ученику через успешную практику оценить свой потенциал.
Муниципальное специальное (коррекционное) общеобразовательное учреждение
«Юровская специальная (коррекционная) общеобразовательная школа-интернат VI вида»
Раменского муниципального района
Утверждаю Согласовано Рассмотрено
Директор Юровской школы-интерната Зам. директора по УВР на заседании ШМО
__________ Сорокина В.Н. _____________ Минкина Л.Н. протокол № ________
от ________________
Руководитель ШМО
___________ Кракасевич М.М.
Тематическое и почасовое планирование образовательных результатов освоения алгебры
на 2012/2013 учебный год (фрагмент)
Класс: 8
Учитель: Скворцова Ольга Викторовна
Количество часов: на учебный год: _102_в неделю:_3_
Плановых контрольных уроков: : I ч. – 2; II ч. – 2 ; III ч. – 3 ; IV ч. – 3.
Планирование составлено на основе источников:
1)Программа: Программы общеобразовательных учреждений: Алгебра 7-9 классы Составитель: Бурмистрова Т. А. - М. Просвещение 2009 г.
2) Учебник Алгебра: учеб. для 8 кл. общеобразоват. Учреждений/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С. А. Теляковского. – М.: Просвещение, 2008.
3)Жохов В.И. Дидактические материалы по алгебре для 8 класса/ В.И. Жохов, Ю.Н. Макарычев, Н.Г. Миндюк. - М.: Просвещение, 2008.
4) Жохов В.И. Уроки алгебры в 8 классе: кН. Для учителя (В.И. Жохов, Г.Д. Карташева. – М.: Просвещение, 2008.
5) Сборник заданий для проведения письменного экзамена по алгебре за курс основной школы, 9 класс Л.В. Кузнецова, Е.А. Бунимович, Б.П. Пигарев, С.Б. Суворова. — М.: Дрофа, 2009.
Тематическое планирование составил: Скворцова О.В. Дата 2012 Роспись _____________
Условные обозначения: ПУУД – познавательные УУД; ПЛ УУД - познавательные логические УУД; ПО УУД - познавательные общеучебные УУД; РУУД – регулятивные УУД; КсУУД – коммуникативные УУД сотрудничество; КрУУД – коммуникативные УУД для общения: развитие устной и письменной речи; Ц1 – Ц 5 – цель 1 – 5; ДЗ – домашнее задание; УПД – учебно-познавательная деятельность.
№ уро-
ков
|
Раздел, тема урока
|
Форма урока; форма обучения
|
Предметные и метапредметные результаты
Ц 1 (ПЛ УУД), Ц 2 (ПО УУД, РУУД), Ц 3 , Ц 4 (КсУУД, КРУУД), Ц 5 (ПОУУД, РУУД)
|
1 - 11
|
Название темы «Квадратные уравнения»
Средства обучения
Учебник, таблицы, способы решения неполных квадратных уравнений;
Решение квадратных уравнений по алгоритму, схемы, карточки, приёмы саморегуляции при выполнении преобразований и решении уравнений, электронные средства, карта темы.
|
Уроки: семинар, практикум, лекция, др.
Фронтальная, индивидуальная
групповая
формы обучения
|
Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении: а) понятий; б) теорем; в) типов задач
Ц 2: контроль усвоения теоретических знаний: а) геометрических понятий; б) теорем; в) типов и классов задач
Ц 3: применение знаний и интеллектуальных умений при решении геометрических и учебных задач
Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
Ц 5: развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД
|
1
|
Определение квадратного уравнения. Неполные квадратные уравнения.
|
Урок смешанного типа
Фронтально-индивидуальная
|
Ц 5: введение в тему, постановка и формулирование целей своей учебной деятельности; развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД);
Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении понятий квадратное уравнение (полное, приведённое и неполное)
|
2
|
Определение квадратного уравнения. Неполные квадратные уравнения.
|
Практикум: фронтальная, индивидуальная и
групповая работа
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения (полные, неполные), виды неполных квадратных уравнений;
Ц 3: применение знаний и интеллектуальных умений при решении неполных квадратных уравнений;
Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
3
|
Формула корней квадратного уравнения
|
Лекция-диалог, форма обучения фронтально-индивидуальная
|
Ц 5: введение в тему, постановка и формулирование целей своей учебной деятельности; развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД);
Ц 1: приобретение учебной информации и развитие интеллектуальных умений при изучении понятий квадратное уравнение, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов .
Ц 2: контроль усвоения изученного материала в процессе чтения лекции
|
4
|
Формула корней квадратного уравнения
|
Урок смешанного типа
Фронтально-индивидуальная, групповая
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов ;
Ц 3: применение знаний и интеллектуальных умений при решении квадратных уравнений;
Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
5
|
Формула корней квадратного уравнения
|
Практикум: фронтальная, индивидуальная и
групповая работа
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов ;
Ц 3: применение знаний и интеллектуальных умений при решении квадратных уравнений;
Ц 4: развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
6
|
Самостоятельная работа
|
Практикум: индивидуальная работа
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов ;
Ц 3: применение знаний и интеллектуальных умений при решении квадратных уравнений;
Ц 4: развитие коммуникативных умений через: организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
7
|
Решение задач с помощью квадратных уравнений
|
Практикум: фронтальная, индивидуальная и
групповая работа
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов ;
Ц 3: применение знаний и интеллектуальных умений при решении задач с помощью квадратных уравнений;
Ц 4: : развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
8
|
Решение задач с помощью квадратных уравнений
|
Практикум: фронтальная, индивидуальная и
групповая работа
|
Ц 2: контроль усвоения теоретических знаний квадратные уравнения, формула корней квадратного уравнения, дискриминант, формула корней квадратного уравнения с четным вторым коэффициентов, использует предписания для решения типов задач своего уровня сложности;
Ц 3: применение знаний и интеллектуальных умений при решении задач с помощью квадратных уравнений, решает задачи своего уровня сложности;
Ц 4: : развитие коммуникативных умений через: включение в групповую работу; взаимопомощь, рецензирование ответов; организацию взаимоконтроля и взаимопроверки на всех этапах УПД
|
9
|
Теорема Виета
|
Лекция-диалог, форма обучения фронтально-индивидуальная
|
Ц 5: введение в тему, постановка и формулирование целей своей учебной деятельности; развитие организационных умений (целеполагание, планирование, реализация плана, саморегуляция УПД);
Ц 1: составление плана и схем поиска доказательства теоремы Виета и обратной ей, решение квадратных уравнений с помощью теоремы Виета.
Ц 2: контроль усвоения изученного материала в процессе чтения лекции
|
10
|
Теорема Виета
|
Практикум: фронтальная, индивидуальная и
групповая работа
|
Ц 2: использует предписания для решения типов задач своего уровня сложности;
Ц 3: решает задачи своего уровня сложности;
Ц 4: рецензирует ответы товарищей по выполненным заданиям предыдущих уровней с обоснованием; оказывает помощь, работающим на предыдущих уровнях;
Ц 5: выбирает задачи и решает их, осуществляет самопроверку с использованием образцов, приёмов; составляет контрольную работу для своего уровня усвоения (в качестве ДЗ);
|
11
|
Контрольная работа «Квадратные уравнения»
|
Практикум.
Индивидуальная
|
Ц 2, 3, 5: выбирает задачи своего уровня сложности , решает их, осуществляет самопроверку; делает выводы о качестве собственных знаний, необходимых для выполнения контрольной работы
|
Внеурочная самостоятельная деятельность:
|
I. Тематика для подготовки рефератов, выступлений на конференцию, математический вечер, декаду математики и др. (по итогам изучения курса за четверть, за 1-е полугодие, за год)
Теорема Виета, Франсуа Виет, биография французского математика. Из истории: Квадратные уравнения Древнего Египта, Древнего Вавилона, Древней Греции, Древней Индии (занимательная задача про обезьянок), Древнего Китая, Средневекового Востока, Европы.
|
§ 6. Примеры реализации целей обучения теме
«Квадратные уравнения»
Работая по Стандартам второго поколения, мы должны перестроить свой урок. Ученику не дается готовый материал, а создается такая ситуация на уроке, где ребёнок должен Сам: сам задать и ответить на вопрос: «Зачем ему это надо? Зачем ему этот материал?»; сам, сталкиваясь с проблемой, находить пути её решения и средства, с помощью чего он их достигнет. Учитель на уроке выступает уже в роли помощника, наталкивая на ту или иную деятельность.
Поэтому современные уроки могут содержать постановку проблемы; возможные пути её решения, чтобы ученик сам определялся с дальнейшими действиями; схемы, классификацию понятий, задания на соотнесение; задания и действия, условия, которые заставляли учащегося мыслить.
В проекте «Реализация требований ФГОС ООО при обучении учащихся 8 класса теме: «Квадратные уравнения» представлены два урока по теме: «Определение квадратного уравнения. Неполные квадратные уравнения» и «Решение квадратных уравнений по формуле»
"Определение квадратного уравнения.
Неполные квадратные уравнения".
Тип урока Урок усвоения новых знаний
Цели урока.
- ввести определение квадратного уравнения;
уметь определять по внешнему виду уравнения, является ли оно квадратным или нет;
уметь определять значения коэффициентов a, b и c;
уметь отличать полные квадратные уравнения от неполных;
уметь определять тип неполного квадратного уравнения и выбирать алгоритм его решения;
научиться решать неполные квадратные уравнения;
закрепить и систематизировать полученные знания в ходе выполнения упражнений;
развитие памяти, логического мышления;
уметь проводить классификацию уравнений по общему виду;
уметь выделять общее и находить различия;
уметь проводить взаимоконтроль и самоконтроль;
уметь работать в группах и парах, развивая взаимовыручку, умение выслушивать мнения товарищей, отстаивать свою точку зрения.
Оборудование: учебник «Алгебра8 кл.», мультимедийный проектор, карточки с заданиями, листочки (зелёного, синего и жёлтого цвета).
Ход урока:
I.Организационный момент.
Цель: обеспечить положительный эмоциональный настрой.
II. Актуализация опорных знаний. Проверка домашнего задания.
Цель: установить правильность и осознанность выполнения домашнего задания всеми учащимися, выявить пробелы и их коррекция; актуализировать знания о решение линейных уравнений; зафиксировать индивидуальное затруднение в деятельности, демонстрирующее на личностно-значимом уровне недостаточность имеющихся знаний.
Решить, если возможно, уравнения и выписать в отдельные группы те, которые вы можете свести к одному и тому же виду:
1. 5x = -60
2. 5x2 – 9x + 4 = 0
3. 3х2 – 12 = 0
4. 5x2 = 0
5. 6(t-1)=9,4-1,7t
6. 4х2 + 9х = 0
7. x2 + 3x – 10 = 0
8. 3y+y2-8=y2+y+6
9. х2-6х=-2(5+3х)
10. (2х-3)2-2х(4+2х)=49
На слайде первое задание.
В домашней работе вам нужно было решить, если возможно, уравнения и выписать в отдельные группы те, которые вы можете свести к одному и тому же виду. Поднимите руку, кому удалась классификация. Кому удалось выделить только одну группу? Выпишите на доске номера уравнений, вошедших в неё? У кого получилось две группы? Выпиши номера уравнений, вошедших в них. У кого больше? Сколько? Выпиши номера на доске.
Посмотрите, в первой группе (1, 5, 8, 10) такие разные уравнения, а вы их записали вместе. Почему? (Они сводятся к одному и тому же виду?)
Кто сможет записать на доске этот одинаковый вид каждого из уравнений?
Как называются уравнения, к которым можно их свести? (Линейные).
А какой общий вид линейного уравнения? (ах+b=0).
На слайде общий вид линейного уравнения.
В чём же отличие данных уравнений от линейных? (В правой части нет нуля, а в левой - числа).
Как можно их свести к линейным? (Перенести слагаемое из левой части в правую).
Что при этом должно произойти со знаком слагаемого? (Он должен измениться на противоположный).
Посмотрите, на слайде показаны получившиеся линейные уравнения.
5х+60=0
7,7t-15,4=0
2y-14=0
-20х-40=0
Назовите, чему равны в них коэффициенты а и b.
Какие тождественные преобразования вам пришлось совершать при решении уравнений? (Переносить слагаемые из одной части уравнения в другую, изменяя их знаки на противоположные. Умножать и делить левую и правую части на одно и то же число, отличное от нуля).
Итак, четыре таких различных уравнений путём тождественных преобразований можно свести к одному - линейному, алгоритм решения которого хорошо известен. А другие(ую) группы(у) домашних уравнений вы можете свести к одному и тому же виду? (Нет).
А все ли уравнения вы смогли решить? (Нет).
Теперь проверьте домашнее задание. Корни уравнений, которые вы могли решить - на слайде.
Слайд.
х=-12
t=2
y=7
х=-2
Поднимите руку, кто все правильно решил, кто допустил ошибки.
Физминутка для глаз (работа с электронным тренажёром для глаз).
УУД: общепознавательные: общеучебные осознанное построение речевого высказывания;
регулятивные: контроль в форме сличения результата с заданным эталоном с целью обнаружения отклонений и отличий от эталона, коррекция.
III. Восприятие и первичное закрепление нового материала.
Цель: организовать коммуникативное взаимодействие в ходе которого выявляется и фиксируется отличительное свойство задания вызвавшего затруднений в учебной деятельности; согласовать цель и тему урока; обеспечить восприятия осмысления и первичного запоминания знаний и способов действий, связей и отношений в объекте изучения.
- Сегодня вы убедитесь, что и оставшиеся шесть уравнений - это так же уравнения одного и того же вида. Попробуйте дать им имя. (Квадратные уравнения).
Запишите в тетрадях тему сегодняшнего урока: "Определение квадратного уравнения. Неполные квадратные уравнения"
Записать тему урока на доске.
Зная тему урока, давайте попробуем определить цели урока. Раз в теме написано "определение квадратного уравнения", значит в первую очередь, что вам предстоит сделать? (Выучить определение).
Если написано "неполные квадратные уравнения", значит… (Есть и полные).
А раз есть те и другие, то чему вы должны научиться? (Отличать их друг от друга).
Итак, перед вами сегодня на уроке стоят следующие цели: 1) выучить определение квадратного уравнения, 2) научиться определять по виду уравнения является ли оно квадратным или нет, 3) научиться определять вид квадратного уравнения - полное оно или неполное, 4) научиться выбирать нужный алгоритм решения неполного квадратного уравнения.
Слайд с целями урока.
Значение квадратного уравнения в науке трудно переоценить. Умение решать его не раз выручит вас не только на алгебре или геометрии, но и на уроках физики, химии и даже информатики.
Но вернёмся к уравнениям, которые вы не смогли решить дома.
Слайд демонстрирует их.
Что в них можно выделить общего? (1) есть х2, 2) есть х, 3) в правой части 0, 4) есть число.)
Слайд с пунктами и выделением общих элементов.
А чем отличаются данные уравнения? (Числовыми коэффициентами при х и числом).
Т.к. эти числа разные, то математики договорились обозначать коэффициент при х2 через а, при х - через b, число - через с. Тогда оба уравнения можно будет представить в виде: ax2+bx+c=0.
Слайд с буквами.
А как вы думаете, любыми ли числами могут быть а, b и с? (Нет, а не может быть 0).
Почему? (Уничтожается х2).
Есть ли ещё какие-нибудь ограничения на значения а, b и с? (Нет.)
Итак, определение квадратного уравнения.
1 уровень: с помощью учебника с.111§8 п.21
2 уровень: без учебника дополнить
Квадратным уравнение называется уравнение вида ax2+bx+c=0, где:
1) х - ,
2) a, b, c - ,
3) а .
3 уровень: самостоятельно дать определение квадратного уравнения.
Проверка.
Записывается на доске.
Запишите определение квадратного уравнения в тетради.
Коэффициенты a, b и с носят специальные названия: а - первый коэффициент, b - второй коэффициент, с - свободный член.
А только ли икс мы можем обозначать переменную? (Нет).
Кто сможет записать на доске общий вид квадратного уравнения, где переменная будет обозначена другой буквой?
Какое выражение стоит в левой части уравнения? (Сумма).
Какое преобразование можно делать с суммой, и при этом не изменится её значение? (Переставлять местами слагаемые).
Кто тогда сможет написать на доске, как может выглядеть квадратное уравнение иначе? (с+ax2+bx=0, и т.д.)
На следующем слайде представлено несколько уравнений. Выпишите из них те, которые являются квадратными.
3,7х2-5х+1=0,
48х2-х3-9=0,
1-12х=0,
2,1х2+2х-2/3=0,
7/х2+3х-45=0,
7х2-13=0,
х23+12х-1=0.
Почему другие уравнения не будут квадратными? (Они другого вида).
К найденным квадратным уравнениям я добавлю еще несколько уравнений. Все они представлены на слайде.
Слайд:
3,7х2-5х+1=0,
-х2=0,
2,1х2-2/3+2х=0,
7х2-13=0,
-х2-8х+1=0,
-10+3х+х2=0,
х2/7-3х=0.
Подумайте, все ли они квадратные? (Да). Почему? (Т.к. их можно привести к виду ax2+bx+c=0, где х - переменная, a, b, c R, а0).
Для каждого предложенного уравнения выпишите значения коэффициентов а=, b=, с=.
Проверьте друг у друга ответы и исправьте ошибки. Правильные ответы на слайде.
Слайд демонстрирует ответы.
А теперь придумайте и запишите каждый своё квадратное уравнение. Постарайтесь для коэффициентов использовать любые допустимые значения.
Проверьте друг у друга - а квадратные ли уравнения получились, если нет - исправьте ошибку.
Один из учеников запишет своё уравнение на доске.
Итак, коэффициенты b и c в отличие от а могут быть и нулями. Что произойдёт в этом случае с общим видом квадратного уравнения? (В этом случае в квадратном уравнении пропадает одно или несколько слагаемых).
Тогда как можно назвать получающиеся уравнения? (Неполными).
Запишем в тетрадях: если в квадратном уравнении хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называется неполным квадратным уравнением.
Что значит "хотя бы один"? (Один или больше).
От чего же зависит вид неполного квадратного уравнения? (От того, какой коэффициент - b или с - равен нулю).
Давайте рассмотрим все возможные варианты.
1 уровень: с помощью учебника с.112 выписывает виды неполных квадратных уравнений.
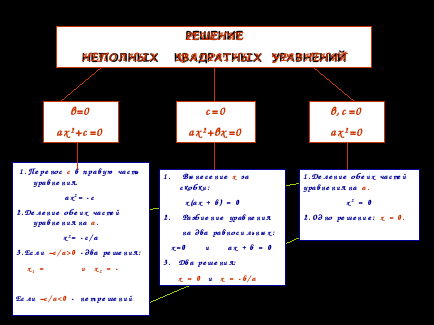
2 уровень: Неполные квадратные уравнения бывают трёх видов:
, где с0
, где b0
,где с=0 и b=0
3 уровень: самостоятельно записывают виды неполных квадратных уравнений.
Проверка: соответствующий слайд с неполными квадратными уравнениями.
На предложенном слайде выберите неполные квадратные уравнения и выпишите себе в тетрадь под каждым видом неполного квадратного уравнения соответствующий порядковый номер найденного уравнения. Один человек выполняет работу у доски с листочками.
Слайд:
3,7х2-5х+1=0,
-х2=0,
2,1х2+2х-2/3=0,
7х2-13=0,
-х2-8х+1=0,
-10+3х+х2=0,
х2/7-3х=0.
Подумайте, а не сталкивались ли мы уже с неполными квадратными уравнениями? (Да, в домашней работе). Теперь нам осталось только записать решение таких уравнений в общем виде.
А как можно назвать не выбранные уравнения? (Полные).
Решать их вы научитесь уже через пару уроков.
Итак, ax2+c=0, где с0.
Прочитайте текст на стр. 112 .
Решим неполные уравнения, которые встретились у вас в домашней работе.
Записывается решение и проговаривается алгоритм.
3х2 – 12 = 0
Перенесем свободный член в правую часть
3х2=12
Разделим обе части уравнения на 3
х2=4
Отсюда х=2 или х=-2
Ответ: х1=2, х2=-2.
х2-6х=-2(5+3х)
х2+10=0
Перенесем свободный член в правую часть
х2=-10
Так как квадрат числа не может быть отрицательным число, то получившееся уравнение не имеет корне. А следовательно, не имеет корней и равносильное ему уравнение х2+10=0.
Ответ: корней нет.
- 1) перенести свободный член в правую часть, 2) разделить обе части уравнения на а0, 3) если -с/а>0, то два корня х1=-с/а и х2=--с/а; если -с/а<0, то корней нет, 4) записать ответ.
Слайд демонстрирует алгоритм.
Значит, сколько может быть корней в неполном квадратном уравнении такого вида? (Два или вообще нет корней).
Решите неполное квадратное уравнение, применяя данный алгоритм: I - 515(а), II - 515(д). Теперь проверьте свои решения, сравнив с решениями на слайде, исправив ошибки.
Слайд.
Следующий вид неполного квадратного уравнения: ax2+bx=0, где b0.
Из домашней работы:
4х2 + 9х = 0
Записывается решение и проговаривается алгоритм.
1) разложить левую часть на множители, 2) используя условие равенства произведения нулю, уравнение заменяется на два уравнения, 3) решается каждое, 4) записывается ответ.
Слайд демонстрирует алгоритм.
Сколько корней всегда будет в таком уравнении? (Два).
Причём один из них обязательно какой? (Нуль).
Решите неполное квадратное уравнение, применяя этот алгоритм: I - 517(а), II - 517(б). Теперь проверьте свои решения, сравнив с решениями на слайде, исправив ошибки.
Слайд.
Последний тип неполного квадратного уравнения ax2=0.
Из домашней работы:
5x2 = 0
Записывается решение и проговаривается алгоритм.
1) разделим обе части на а0, 2) х2=0, х=0, 3) записать ответ.
Слайд демонстрирует алгоритм.
Сколько корней в таком неполном квадратном уравнении? Какой? (Один, нуль).
 |
|
|
 Скачать 0.58 Mb.
Скачать 0.58 Mb.