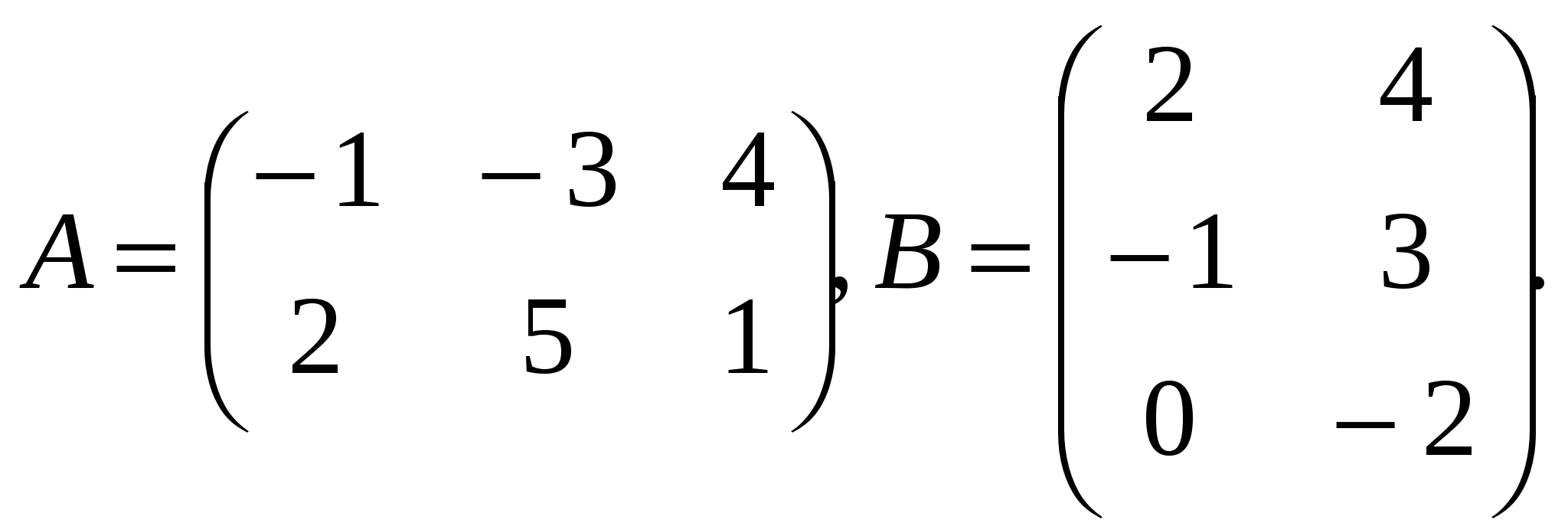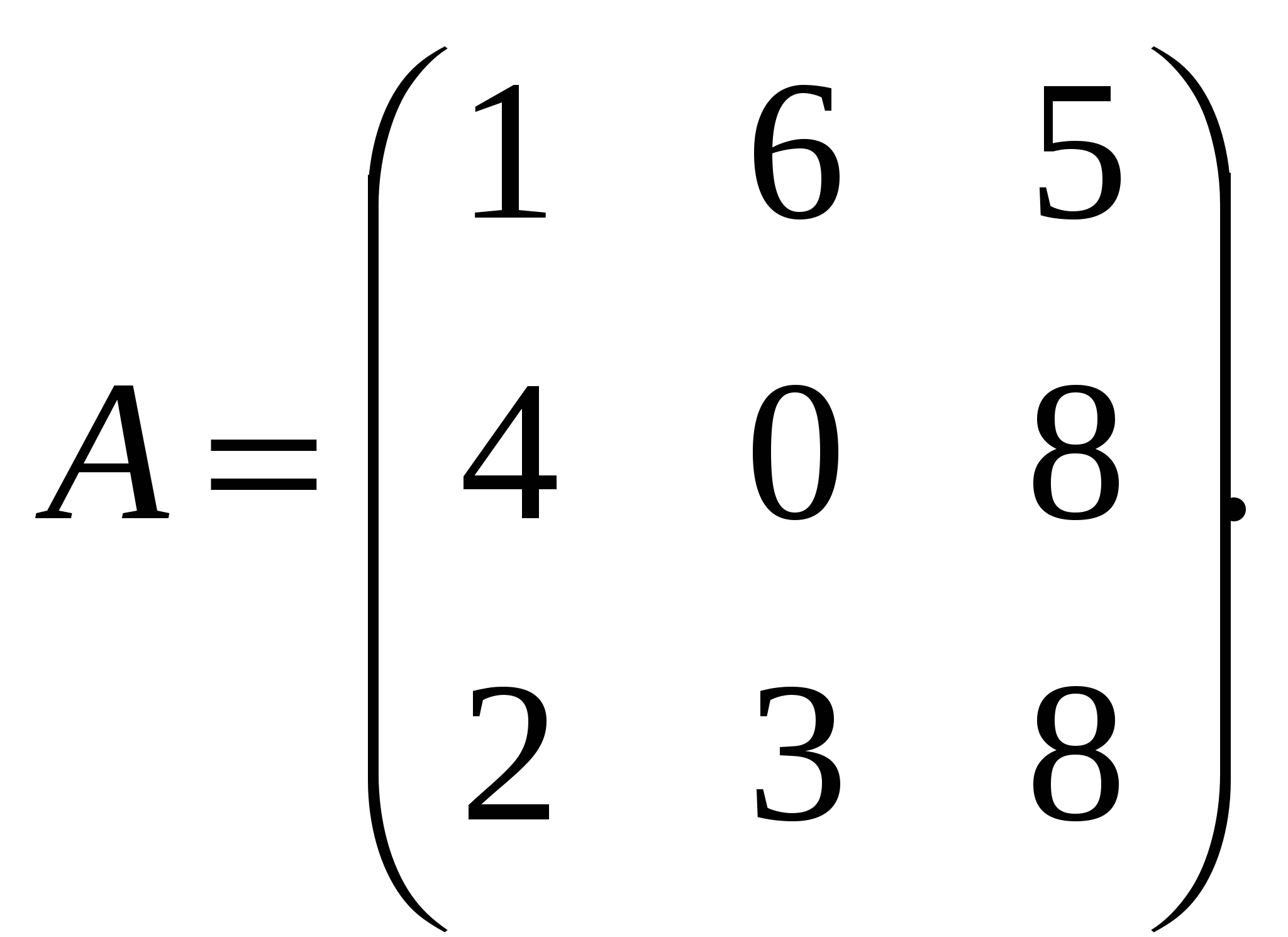Методические рекомендации по выполнению контрольной работы по дисциплине «Прикладная математика»
 Скачать 365.62 Kb. Скачать 365.62 Kb.
|
| «Омский летно-технический колледж гражданской авиации имени А.В. Ляпидевского» филиал Федерального государственного бюджетного образовательного учреждения высшего профессионального образования «Ульяновское высшее авиационное училище гражданской авиации (институт)» (ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И))  МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ и задания для выполнения КОНТРОЛЬНой работы для КУРСАНТОВ, обучающихся по заочной форме по дисциплине «Прикладная математика» Специальность 11.02.06 Техническая эксплуатация транспортного радиоэлектронного оборудования (по видам транспорта) Разработал: Пищагина Е.С., преподаватель математики Рассмотрено на заседании ЦМК ЕНД от «_____»__________20__г. Протокол №_________ Омск – 2015 АННОТАЦИЯ Методические рекомендации по выполнению контрольной работы по дисциплине «Прикладная математика», для курсантов заочного отделения, составлены в соответствии с требованиями Федерального государственного образовательного стандарта специальности и на основании программы учебной дисциплины ЕН.01, Прикладная математика (рассмотрена и утверждена на заседании ЦМК ЕНД «____» ___________20____г., протокол № ___) Методические рекомендации по выполнению контрольных работ предназначены для курсантов 1 курса по специальности: 11.02.06 Техническая эксплуатация транспортного радиоэлектронного оборудования (по видам транспорта). Задания контрольных работ соответствует основным разделам программы, их выполнение обеспечивает более глубокое изучение материала, направлено на закрепление и систематизацию знаний, умений и формирование общих компетенций. Виды заданий включают работу с понятийным аппаратом, вопросами по теме, решение примеров и задач, выполнение расчетно-графической работы. Рецензент: ____________, председатель ЦМК ЕНД ОЛТК ГА филиала ФГБОУ ВПО УВАУ ГА (И) СОДЕРЖАНИЕ АННОТАЦИЯ 3 СОДЕРЖАНИЕ 4 2.Пояснительная записка 5 3. Методические указания по изучению учебного материала 6 4.Методические указания и задания для контрольной работы 13 Таблица выбора вариантов 13 5.Краткие теоретические сведения 21 Определитель второго порядка- это число, равное значению выражения 25 Определитель третьего порядка- это число, равное значению выражения 25 6.Список вопросов к экзамену 31 7.Примерные практические задания к экзамену 33 8.Библиографический список 36
Методические рекомендации и задания по выполнению контрольной работы по дисциплине «Прикладная математика» предназначены для курсантов 1-го курса специальности 11.02.06 - Техническая эксплуатация транспортного радиоэлектронного оборудования (по видам транспорта), обучающихся по заочной форме. Выполнение домашней контрольной работы является обязательным для каждого курсанта, её содержание определяется действующим рабочим учебным планом ОЛТК ГА филиал ФГБОУ ВПО УВАУ ГА (И)). Реализуемые цели выполнения контрольной работы:
Критериями оценки результатов контрольной работы курсанта являются:
Раздел 1. Математического анализ Тема 1.2. Производная и дифференциал функции Понятие производной функции одно из важных понятий в математическом анализе. Для умения решать прикладные задачи с использованием элементов дифференциального исчисления необходимо знать правила дифференцирования, таблицу дифференциалов и правило производной сложной функции. Также важно знать геометрический и физический смысл производной. Для исследования функций с помощью производной и построения графика можно использовать следующую схему: 1) Найти область определения функции. 2) Проверить функцию на четность или нечетность, периодичность. 3) Найти асимптоты графика функции, 4) Найти точки пересечения график функции с осями координат. 5) С помощью первой производной найти промежутки монотонности, ее экстремумы. 6) С помощью второй производной найти промежутки выпуклости и вогнутости, точки перегиба. 7) По результатам исследования построить график функции. Вопросы для самоконтроля:
Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 103. Глава 9, стр. 270. Тема 1.3. Неопределенный и определенный интеграл Понятие первообразной функции одно из важных понятий в математическом анализе. Для решения прикладных задач с использованием элементов интегрального исчисления необходимо знать понятие первообразной, определённого и неопределённого интегралов Для применения данной темы нужно освоить свойства неопределённого и определённого интегралов, методы интегрирования и таблицу интегралов. Для решения прикладных задач при помощи интегралов необходимо знать геометрический и физический смысл неопределенного и определенного интегралов. Вопросы для самоконтроля:
Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 103. Глава 10, стр. 309. Раздел 3. Теория комплексных чисел Тема 3.1. Комплексные числа. Формы записи комплексного числа и операции над ними Для усвоения данной темы необходимо разобрать определение комплексного числа и геометрическую интерпретацию комплексного числа. Действия над комплексными числами в алгебраической форме не представляет сложных преобразований. Чтобы освоить действие над комплексными числами в тригонометрической и показательной форме необходимо повторить тригонометрические и показательные функции. Вопросы для самоконтроля:
Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 103. Глава 16, стр. 484. Раздел 4. Линейная алгебра Тема 1.1. Матрицы, определители. Понятие матрицы одно из важных понятий линейной алгебры. Для усвоения действий над матрицами достаточно знать алгебраические действия: сложение, вычитание, умножение и деление на число, умножение матриц. При изучение данной темы нужно необходимо хорошо усвоить понятие определителей второго и третьего порядков, основные свойства определителей, которые уместно применять при вычислений миноров, алгебраических дополнений и решении систем линейных уравнений с помощью формул Крамера и матричным способом Вопросы для самоконтроля
Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 92, 103. Тема 1.2. Решение систем линейных алгебраических уравнений При изучении данной темы необходимо обратить внимание на способы нахождения обратной матрицы: 1) с помощью алгебраических дополнений; 2) с помощью линейных преобразований над строками матрицы. Операция обращения матрицы применяется при решении матричных уравнений. При изучении данной темы также следует обратить внимание на основные методы решения СЛАУ:
Вопросы для самоконтроля:
Литература:
Раздел 5. Теория вероятностей и математическая статистика Тема 5.1. Теория вероятностей Перед разбором основных понятий комбинаторики необходимо разобрать понятие факториала. Уметь выполнять преобразования с факториалами. Для освоения понятий комбинаций: перестановки, размещения, сочетания нужно знать вывод формул для определения этих величин. Элементы комбинаторики необходимы при решении задач в теории вероятности. В данной теме необходимо усвоить виды событий. Так как при определении вероятности очень важно знать различия между событиями, для которых по разным теоремам определяется вероятность. Важно уметь определять вероятность события по классической формуле. Вопросы для самоконтроля
Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 103. Глава 15, стр. 442. Тема 5.2. Случайная величина, её функция распределения При изучении данной темы необходимо правильное применение теорем и формул вероятности, изученных в предыдущей теме. При рассмотрении функции и графика непрерывной случайной величины важно правильное построение графика распределения. Изучение числовых характеристик даёт полную картину о случайных величинах. Вопросы для самоконтроля Сформулировать определение дискретной и непрерывной случайных величин. Что такое плотность распределения вероятностей? Каким свойством обладает плотность распределения вероятностей? Как связаны между собой плотность распределения и интегральная функция распределения? Перечислить свойства интегральной функции. Дать определения числовым характеристикам СВ. Литература: Математика: Учебник для студентов образовательных учреждений сред. проф. образования/ А.А. Дадаян. – М.Форум, 2011. - 544 с. - (Профессиональное образование), стр. глава 4, стр. 103. Глава 15, стр. 468.
3.1. Общие методические указанияКонтрольная работа должны выполняться в отдельной тетради на клетчатой бумаге. Работа, выполненная небрежно, будет возвращена курсанту без проверки. На первой странице записать наименование предмета, номер контрольной работы, фамилию и инициалы и адрес. В тетради оставляют поля шириной 4-5 см. Условия всех задач писать полностью. Если требуется чертеж, то его выполняют карандашом, с помощью чертежных инструментов. При построении чертежа соблюдается масштаб. Решение задачи или примера должно сопровождаться необходимыми вычислениями, формулами и пояснениями. Если работа выполнена неудовлетворительно, то курсант исправляет её и представляет вторично, или по указанию преподавателя выполняет другой вариант. Работа, выполненная не по своему варианту, не засчитывается и возвращается без проверки. 3.2. Таблица выбора вариантов контрольной работы Выбор вопросов и заданий к контрольной работе определяется по фамилии, имени и отчеству курсанта, которые записываются в виде таблички, где номер буквы ФИО определяет номер задачи. |