Квадратный корень из дроби
 Скачать 42.92 Kb. Скачать 42.92 Kb.
|
| Мой университет - www.moi-mummi.ru Урок алгебры в 8 классе Тема: Квадратный корень из дроби На уроке используется презентация. Урок проводился в кадетском классе. Цели урока: повторить преобразование выражений, содержащих квадратные корни; изучить теорему о квадратном корне из дроби; научиться применять данную теорему; развитие логического мышления; привитие интереса к предмету математики; развитие познавательной активности учеников. Ход урока: 1. Актуализация знаний (устно) 2. Исторический материал (сообщение учащегося) 3. Изучение нового материала 4. Закрепление материала
5.Решить анаграмму 6. Подведение итогов, домашнее задание
-Начать урок хочется со слов: «Если мы действительно знаем что-то, то мы знаем это благодаря изучению математики» (П.Гассенди) Вы – кадеты, и ,наверное, кто-то из вас собирается связать свою жизнь с военным делом. Но как говорил поэт: «Одной отваги мало, математика нужна!» Устно: (слайды 2-5)
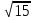 , , 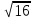 , , 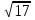 , , 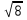 . .
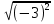 , , 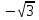 , , 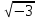 , , 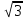 . .
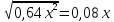 (0,8х) (0,8х)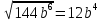 (12 (12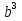 ) )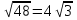 решено верно решено верно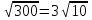 10 10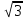 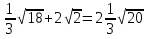 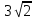 Все рассмотренные выше задания взяты из сборников для подготовки к экзамену по алгебре.
Слово «корень» пришло в математику от арабов. Арабские учёные представляли себе квадрат числа вырастающим из корня – как растение, - и потому называли корнями такие числа. 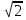 - было первым числом, про которое древнегреческие математики узнали, что оно не выражается в виде обыкновенной дроби. Это открытие настолько поразило, что держалось в строжайшей тайне. Существует легенда, повествующая о том, что математик, разгласивший эту тайну, погиб во время кораблекрушения в море – так он был наказан богами за болтливость. - было первым числом, про которое древнегреческие математики узнали, что оно не выражается в виде обыкновенной дроби. Это открытие настолько поразило, что держалось в строжайшей тайне. Существует легенда, повествующая о том, что математик, разгласивший эту тайну, погиб во время кораблекрушения в море – так он был наказан богами за болтливость.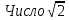 греки получили, вычисляя длину гипотенузы прямоугольного треугольника с катетами равными единице. греки получили, вычисляя длину гипотенузы прямоугольного треугольника с катетами равными единице.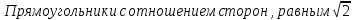 , встречаются при определении формата книг на типографной фабрике. Это соотношение часто используется в архитектуре, например, в пропорциях известного храма Покрова на Нерли. , встречаются при определении формата книг на типографной фабрике. Это соотношение часто используется в архитектуре, например, в пропорциях известного храма Покрова на Нерли.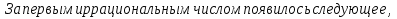 а затем выяснилось, что таких чисел даже больше, чем рациональных. а затем выяснилось, что таких чисел даже больше, чем рациональных. современного знака корня появилось только в 17 веке. Какой математик впервые применил его, вы узнаете, разгадав ребус. современного знака корня появилось только в 17 веке. Какой математик впервые применил его, вы узнаете, разгадав ребус.Мы уже умеем извлекать корень из произведения, а сегодня научимся извлекать квадратный корень из дроби.
Рассмотрим теорему: Если a 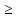 0, b > 0 , то 0, b > 0 , то 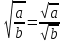 . .Т.е. корень из дроби равен корню из числителя, делённому на корень из знаменателя. Например, 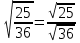 = = 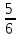 . .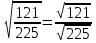 = = 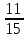 . .По данной теореме при делении корней можно разделить подкоренные выражения и из результата извлечь корень: 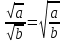 Например, 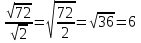 . .
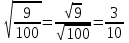 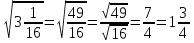 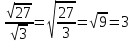 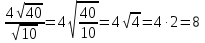
№ 363(1,3) 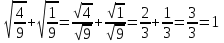 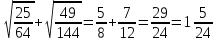
(взаимопроверка результатов) (слайды 16-17) 1 вариант 2 вариант
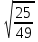 ; ; 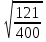 ; ; 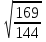 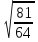 ; ; 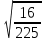 ; ; 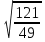
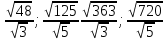
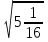 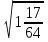 - Обменяйтесь тетрадями с соседом по парте, оцените работу и поставьте оценку. Критерии оценки: «5» - 6 верно решённых примеров «4» - 5 верно решённых примеров «3» - 4 верно решённых примеров -Поднимите руки, кто получил «4» или «5»?
-Что нового вы узнали? -Чему научились? - Решите анаграммы: Чевостоте – отечество Нидаро – родина Датек – кадет Ясирсо – россия Все эти слова объединяет чувство патриотизма. Как воздух, математика нужна. Одной отваги мало. Расчёты! Залп! И цель поражена Могучими ударами металла. И воином любовь сбережена К учителю, далёкому, седому. Как воздух, математика нужна Сегодня офицеру молодому! Домашнее задание: № 363(2,4), 365(2,4). Дополнительное задание к домашней работе: В последнем примере самостоятельной работы требовалось извлечь корень из смешанной дроби. Вообще говоря, вынести целую часть из-под знака корня нельзя, например: 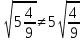 . .Но вот пример, когда такое преобразование корня не приводит к ошибке: 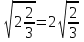 . .Подберите ещё несколько таких примеров. Дополнительные примеры: (слайд 20) Литература:
|