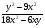Протокол № от Приказ № от г г. г
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
            МБОУ «Хоринская СОШ № 1 имени Д.Ж. Жанаева» МБОУ «Хоринская СОШ № 1 имени Д.Ж. Жанаева»Рассмотрено:_______________ Согласовано: __________________ Утверждаю:_________________ Руководитель МО Буянтуева Н.Г. Зам. директора по МР Садовская С.Г. Директор школы Цыдыпдашиева Л.А. Протокол №_____ от Приказ № ___________ от «_____» ______________г. «_____» ______________г. «___ »________________г. Рабочая программа Предмет: Алгебра Класс: 7 Количество часов: 102 Тип программы: общеобразовательный ФИО учителя: Садовская Светлана Георгиевна с. Хоринск 2011- 2012 учебный год Пояснительная записка Рабочая программа по алгебре разработана на основании Закона РФ «Об образовании» (1992), в соответствии с требованиями Федерального компонента государственного стандарта общего образования и требования к оснащению образовательного процесса (2004г., № 1089), примерной программы по математике общего образования, авторской программы А.Г. Мордковича (2007), учебного плана и локальных актов МБОУ «Хоринская СОШ №1 им. Д.Ж.Жанаева». Рабочая программа составлена для учащихся 7 «в» класса МБОУ «Хоринская СОШ №1 имени Д.Ж.Жанаева», рассчитана на 102 часа в год, 3 часа в неделю. В основу изучения курса положены принципы: дидактические (научности, сознательности и активности, наглядности, систематичности и последовательности, прочности, доступности, связи обучения с жизнью); воспитания (социальной активности, социального творчества, развивающее воспитание, мотивированность, проблемность, индивидуализация, опора на ведущую деятельность); развития (деятельности, непрерывности, целостного представления о мире, минимакса, психологической комфортности, вариативности, творчества); педагогики здоровья: ненанесения вреда; субъект-субъектного взаимоотношения с учащимися; соответствия содержания и организации обучения возрастным особенностям учащихся; гармоничного сочетания обучающих, воспитывающих и развивающих педагогических воздействий; приоритет активных методов обучения; принцип отсроченного результата Изучение алгебры в 7 классе направлено на достижение цели:
Задачи: Обучения: овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования; интеллектуальное развитие; получение школьниками конкретных знаний о функциях как важнейшей математической модели для описания и исследования разнообразных процессов, для формирования у учащихся представлений о роли математики в развитии цивилизации и культурыформирование Развития: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей; математической речи; сенсорной сферы; двигательной моторики; внимания; памяти; навыков само и взаимопроверки. Воспитания: культуры личности, отношения к математике как к части общечеловеческой культуры, понимание значимости математики для научно-технического прогресса; волевых качеств; коммуникабельности; ответственности. Валеологические: сохранение и укрепление здоровья детей; наблюдение за посадкой детей; активное внедрение здоровьесберегающих технологий. Общая характеристика учебного предмета: Алгебра нацелена на формирование математического аппарата для решения задач из математики, смежных предметов, окружающей ре альности. Язык алгебры подчеркивает значение математики как языка для построения математических моделей, процессов и явлений реального мира. В ходе освоения содержания курса учащиеся получают возможность:
В ходе преподавания алгебры в 7 классах, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
Возрастные и психологические особенности учащихся, характеристика класса: Средний школьный возраст – переход от детства к юности. У школьника подростка этот переход связан с включением его в доступные ему формы общественной жизни. Вместе с тем меняется и реальное место, которое ребенок занимает в повседневной жизни окружающих его взрослых, в жизни своей семьи. Теперь его физический силы, его знания и умения ставят его в некоторых случаях на равную ступень с взрослыми, а кое в чём он даже чувствует своё преимущество. Продолжается развитие нервной системы, мыслительной деятельности. Мировоззрение, нравственные идеалы, система оценочных суждений, моральные принципы, которыми школьник руководствуется в своем поведении, еще не приобрели устойчивость, их легко разрушают мнения товарищей, противоречия жизни. Правильно организованному воспитанию принадлежит решающая роль. В зависимости от того, какой нравственный опыт приобретает подросток, будет складываться его личность. В классе обучается 21 ученик: 10 мальчиков и 11 девочек. По итогам обследования учащихся выявлено, что 4 учащихся имеют низкий уровень обученности, остальные- средний уровень. Исходя из этого, созданы условия для сохранения и развития здоровья всем учащимся, составлены индивидуальные (траектории) программы работы с детьми с низким уровнем готовности к обучению в школе и пониженной мотивацией, а также подобраны педагогические технологии и методы, описанные ниже. В программе используются педагогические технологии: технологии на основе активизации и интенсификации деятельности учащихся (игровые технологии); технологии на основе активизации и интенсификации деятельности учащихся (системы развивающего обучения с направленностью на развитие творческих качеств личности); технологии на основе эффективности управления и организации учебного процесса (технология уровневой дифференциации обучения на основе обязательных результатов). Методы :
Формы текущего и итогового контроля: самостоятельная работа, тестирование, теоретические диктанты, контрольные работы. Учебно-тематический план
СОДЕРЖАНИЕ ТЕМ УЧЕБНОГО КУРСА
Числовые и алгебраические выражения. Переменная. Допустимое значение переменной. Недопустимое значение переменной. Первые представления о математическом языке и о математической модели. Линейные уравнения с одной переменной. Линейные уравнения как математические модели реальных ситуаций. Координатная прямая, виды промежутков на ней. Основная цель изучения данной темы – выработать у учащихся умение выполнять действия над степенями с натуральным показателем.
Координатная плоскость. Алгоритм отыскания координат точки. Алгоритм построения точки М(а;b) в прямоугольной системе координат. Линейное уравнение с двумя переменными. Решение уравнение. График уравнения. Алгоритм построения графика уравнения. Линейная функция. Независимая переменная (аргумент). Зависимая переменная. График линейной функции. Наибольшее и наименьшее значения линейной функции на заданном промежутке. Возрастание и убывание линейной функции. Взаимное расположение графиков линейных функций.
Система уравнений. Решение системы уравнений. Графический способ решения уравнений. Метод подстановки. Метод алгебраического сложения. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций (текстовые задачи)
Степень. Основание степени. Показатель степени. Свойства степени с натуральным показателем. Умножение и деление степеней с одинаковыми показателями. Степень с нулевым показателем. 5 . Одночлены. Операции над одночленами (8 часов) Понятие одночлена. Коэффициент одночлена. Стандартный вид одночлена. Подобные одночлены. Арифметические операции над одночленами.
Многочлен. Члены многочлена. Двучлен. Трехчлен. Приведение подобных слагаемых членов многочлена. Стандартный вид многочлена. Формулы сокращенного умножения. Деление многочлена на одночлен.
Разложение многочлена на множители: с помощью формул сокращенного умножения, способ группировки, вынесение общего множителя за скобки, комбинированный способ. Метод выделения полного квадрата. Основная цель изучения данной темы - выработать умение выполнять сложение, вычитание, умножение многочленов и разложение многочлена на множители. Данная тема играет фундаментальную роль в формировании умения выполнять тождественные преобразования алгебраических выражений. Понятие алгебраической дроби. Сокращение алгебраической дроби. Тождество. Тождественно равные выражения. Тождественные преобразования.
Квадратичная функция, ее свойства и график. Графическое решение уравнений. Кусочная функция. Чтение графика функции. Область определения функции. Первое представление о непрерывных функциях. Точка разрыва. Функциональная символика.
Учебно-методическое обеспечение Список литературы для учителя Основная литература:
Дополнительная литература: 1. «Нестандартные задания по математике 5 – 11 классы», В.В. Кривоногов. 2. «Математика, итоговые уроки 5-9 классы», О.В. Бощенко. 3. «Математические олимпиады в школе 5-11 классы», А.В. Фарков. 4. Тесты по математике 5-11 классы, М.А. Максимовская и др. 5. «Учитесь мыслить нестандартно», Б.М. Абдрашитов и др. 6. «Интеллектуальные турниры, марафоны, бои», библиотека «Первого сентября», 2003 г. 7. «Тесты для промежуточной аттестации 7-8 классы», Ф.Ф. Лысенко, 2007 г. 8. «Я иду на урок математики, 7 класс, алгебра», библиотека «Первого сентября», 2001 г. Интернет ресурсы:
Список литературы для ученика
Контрольно- измерительные материалы Перечень обязательных контрольных работ: Контрольная работа №1: «Выражения, преобразования выражений, тождества» Контрольная работа №2: «Линейные уравнения с одной переменной». Контрольная работа №3: «Линейная функция» Контрольная работа №4: «Степень с натуральным показателем». Контрольная работа №5: «Многочлен». Контрольная работа №6: «Умножение многочленов. Способ группировки». Контрольная работа №7: «Разложение многочлена на множители». Контрольная работа №8: «Системы линейных уравнений с двумя переменными». Итоговая контрольная работа.
1о. Найдите значение алгебраического выражения 4(4с – 3) + 8(5 – 2с) – (10с + 8) при с = 0,12 2о. Решите уравнение: а) 2х + 3 = 0; б) 6х – 7 = 15 + 2х 3о. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Луч с началом в точке (-5). Сколько отрицательных чисел принадлежит данному промежутку? 4о. Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель: А(-3; 1); В(-3; 4) 5. Решите задачу: В книге 190 страниц. В пятницу Знайка прочитал в 1,2 раза меньше страниц, чем в субботу, а в субботу на 20 страниц меньше, чем в воскресенье. Сколько страниц он прочитал в субботу?
1. Найдите значение алгебраического выражения 2(12с – 7) + 6(5 – 4с) – 3(2с + 5) при с = 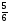 2о. Решите уравнение: а) 3х - 2 = 0; б) 7х + 1,5 = 10х - 3 3о. Запишите обозначение, аналитическую и геометрическую модели числового промежутка: «Открытый луч с концом в точке 7. Сколько натуральных чисел принадлежит данному промежутку? 4о. Постройте прямую, проходящую через данные точки, и запишите ее аналитическую модель: А(-2; 3); В(1; 3) 5. Решите задачу: Капитан Врунгель загрузил на свой корабль в трех ящиках 44 кг бананов. В первом ящике было в 1,5 раза больше бананов, чем во втором, и на 4 кг меньше, чем в третьем. Сколько килограммов бананов в первом ящике?
– 3х + 2у – 6 = 0 с координатными осями и постройте его график. б) Принадлежит ли графику данного уравнения точка К 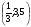 ? ?
б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-1;2].
б) Определите, возрастает или убывает заданная функция. Ответ объясните.
2х - 5у – 10 = 0 с координатными осями и постройте его график. б) Принадлежит ли графику данного уравнения точка М  ? ?
б) Найдите наименьшее и наибольшее значение этой функции на отрезке [-2;1].
б) Определите, возрастает или убывает заданная функция. Ответ объясните.
1о. Решите методом подстановки систему уравнений 3х – у = -5, -5х + 2у = 1. 2о. Решите методом алгебраического сложения систему уравнений 9х + 4у = 8, 5х + 2у = 3. 3о. Решите графически систему уравнений х + у = 5, у = 2х + 2. 4.В туристический поход ребята взяли двухместные и трехместные палатки. Сколько человек разместилось в трехместных палатках, если на 26 человек взяли 10 палаток?. 5. Дана система уравнений ах + by = 36, ax - by = 8. Пара чисел (2;-1) является ее решением. Найти значения a и b.
1о. Решите методом подстановки систему уравнений 4х – 9у = 3, х + 3у = 6. 2о. Решите методом алгебраического сложения систему уравнений 6х - 7у = -2, 2 х – 5у = 2. 3о. Решите графически систему уравнений у = 2х - 1, х + у = -4. 4.В копилку складывали двухрублевые и пятирублевые монеты. Когда копилку вскрыли, в ней оказалось пятирублевых монет на 12 меньше, чем двухрудлевых, а всего денег на сумму 178 руб. Сколько рублей пятирублевыми монетами было в копилке? 5. Дана система уравнений ах – by = -24, ax + by = 4. Пара чисел (1;-2) является ее решением. Найти значения a и b.
1о. Упростить выражение: а) 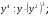 б) б) 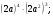 в) в) 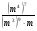
1о. Упростить выражение: а) 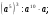 б) б) 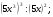 в) в) 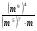
а) 5х2у – 8х2у + х2у б) 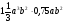 в) в) 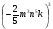 г) г) 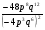
-2ху4х2 + 3х3у22у2 – х2у(-ху3) при х = 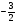 ; у = 2 ; у = 2
а) ху2 – 13ху2 + 5ху2 б)  в) в) 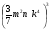 г) г) 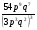
2a2b3(-1,5a3b) + 5a4b4a + a2(-b)4a3 при b = 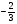 ; a = -3 ; a = -3
р(х) = р1(х) + р2(х) – р3(х) и р1(х) = -2х2 + 3х; р2(х) = 4х2 – 3; р3(х) = 2х – 4.
а) 4ху(2х + 0,5у – ху); б) (х – 3)(х + 2); в) (24х2у + 18х3) : (-6х2)
р(х) = р1(х) + р2(х) – р3(х) и р1(х) = 2х2 - 5х; р2(х) = 3х2 + 1; р3(х) = х – 2.
а) -5ху(3х2 - 0,2у2 + ху); б) (х – 5)(х + 4); в) (35х3у - 28х4) : 7х3
а) 3х2 – 12х б) 2а + 4b – ab – 2b2 в) 4х2 – 9 г) х3 – 8х2 + 16х
а) 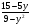 б) б) 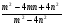
а) 4х2 + 8х б) 3а - 6b + ab – 2b2 в) 9х2 – 16 г) х3 + 18х2 + 81х
а)  б) б) 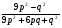
1о. Постройте график функции у = х2. С помощью графика найдите а) значение функции при значении аргумента, равном -2; 1; 3; б) значение аргумента, если значение функции равно 4; в) наибольшее и наименьшее значения функции на отрезке [-1;2]; 2о. Решите графически уравнение х2 = 2х + 3 3о. Дана функция y = f(x), где f(x) = x2. При каких значениях х верно равенство f(x - 4) = f(x + 3)? 4. Дана функция y = f(x), где  х2, если -3 х 2, х2, если -3 х 2,-х + 6, если х > 2. Используя график функции, установите: а) область определения функции; б) наибольшее и наименьшее значения функции в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв; г) промежутки возрастания и убывания функции; д) при каких значениях аргумента у = 0, у < 0, y > 0.
а) значение функции при значении аргумента, равном -3; -1; 2; б) значение аргумента, если значение функции равно 9; в) наибольшее и наименьшее значения функции на отрезке [-3;2]; 2о. Решите графически уравнение х2 = 4х - 3 3о. Дана функция y = f(x), где f(x) = x2. При каких значениях х верно равенство f(x - 2) = f(x + 5)? 4. Дана функция y = f(x), где  х + 3, если х < -1, х + 3, если х < -1,х2, если -1 х 3. Используя график функции, установите: а) область определения функции; б) наибольшее и наименьшее значения функции в) является ли функция непрерывной: если нет, то в каких точках терпит разрыв; г) промежутки возрастания и убывания функции; д) при каких значениях аргумента у = 0, у < 0, y > 0. 5.Постройте график функции 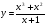
Используя график функции, установите: a) наибольшее и наименьшее значения функции на отрезке [1;2]; б) значения аргумента, при которых у = 0, у < 0.
 х2, если х 2, х2, если х 2,-2х + 8, если х > 2. С помощью графика определите, при каких значениях р уравнение f(x) = р имеет два корня.
Используя график функции, установите: a) наибольшее и наименьшее значения функции на отрезке [0;3]; б) значения аргумента, при которых у = 0, у > 0.
 х + 2, если х < -1, х + 2, если х < -1, x2, если х -1. С помощью графика определите, при каких значениях р уравнение f(x) = р имеет два корня. ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ОБУЧАЮЩИХСЯ В результате изучения курса алгебры, обучающиеся должны знать:
должны уметь:
Обладать базовыми компетенциями: использовать приобретенные знания и умения в практической деятельности и повседневной жизни для: для построения и исследования математических моделей для описания и решения прикладных задач, задач из смежных дисциплин; для выполнения и самостоятельного составления алгоритмических предписаний и инструкций на математическом материале; интерпретация графиков реальных зависимостей между величинами; для совершенствования навыков по использованию справочного материала и простейших вычислительных устройств. Обладать ключевыми компетенциями:
Обладать специальными компетенциями:
Решать следующие жизненно-практические задачи:
КРИТЕРИИ И НОРМЫ ОЦЕНКИ ЗНАНИЙ, УМЕНИЙ И НАВЫКОВ ОБУЧАЮЩИХСЯ ПО МАТЕМАТИКЕ 1. Оценка письменных контрольных работ обучающихся по математике. Ответ оценивается отметкой «5», если:
Отметка «4» ставится в следующих случаях:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Отметка «1» ставится, если:
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий. |
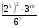
 и 1,6о
и 1,6о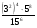
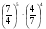 и (-2)о
и (-2)о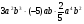
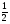 всех мешков, во второй раз он выбросил еще 60% от оставшихся мешков, а в третий раз – последние 4 мешка. Сколько всего мешков с песком брал с собой Незнайка?
всех мешков, во второй раз он выбросил еще 60% от оставшихся мешков, а в третий раз – последние 4 мешка. Сколько всего мешков с песком брал с собой Незнайка?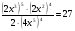
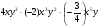
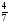 от оставшегося варенья, а в третий – доел последние 270г. Сколько всего граммов варенья было в банке?
от оставшегося варенья, а в третий – доел последние 270г. Сколько всего граммов варенья было в банке?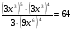
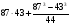
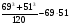
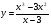
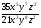 б)
б) 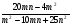
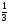 x + 1
x + 1 б)
б)