Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача


Пояснительная записка Рабочая программа линии умк «Математика Сферы»



НазваниеПояснительная записка Рабочая программа линии умк «Математика Сферы»
страница1/7
Е.А.Бунимович
Дата27.02.2016
Размер0.96 Mb.
ТипПояснительная записка
  1   2   3   4   5   6   7



Пояснительная записка

Рабочая программа линии УМК «Математика – Сферы» (5-6 классы), авторы: Е.А.Бунимович и др., М.: Просвещение, 2012, составлена на основе Федерального государственного стандарта общего образования, Фундаментального ядра содержания образования, Примерной программы по математике.

Математическое образование является обязательной и неотъемлемой частью общего образования на всех ступенях школы.

Приоритетными целями обучения математики в 5-6 классах являются:

  • продолжение формирования центральных математических понятий (число, величина, геометрическая фигура), обеспечивающих преемственность и перспективность математического образования школьников;

  • подведение учащихся на доступном для них уровне к осознанию взаимосвязи математики и окружающего мира, пониманию математики как части общей культуры человечества;

  • развитие интеллектуальных и творческих способностей учащихся, познавательной активности, критичности мышления, интереса к изучению математики;

  • формирование умения извлекать информацию, новое знание, работать с учебным математическим текстом.

Изучение математики должно обеспечить:

1)в направлении личностного развития:

  • формирование представлений о математике как части общечеловеческой культуры, о значимости математики в развитии цивилизации и современного общества;

  • развитие логического и критического мышления, культуры речи, способности к умственному эксперименту;

  • формирование интеллектуальной честности и объективности, способности к преодолению мыслительных стереотипов, вытекающих из обыденного опыта;

  • воспитание качеств личности, обеспечивающих социальную мобильность, способность принимать самостоятельные решения;

  • формирование качеств мышления, необходимых для адаптации в современном информационном обществе;

  • развитие интереса к математическому творчеству и математических способностей;

2) в метапредметном направлении:

  • развитие представлений о математике как форме описания и методе познания действительности, создание условий для приобретения первоначального опыта математического моделирования;

  • формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различных сфер человеческой деятельности;

  • развитие умений применять изученные понятия, результаты, методы для решения задач практического характера и задач смежных дисциплин с использованием при необходимости справочных материалов, компьютера, пользоваться оценкой и прикидкой при практических расчетах;

3) в предметном направлении:

  • овладение математическими знаниями и умениями, необходимыми для продолжения образования, изучения смежных дисциплин, применения в повседневной жизни;

  • создание фундамента для математического развития, формирования механизмов мышления, характерных для математической деятельности;

  • понимание роли информационных процессов в современном мире;

  • развитие умений работать с учебным математическим текстом, точно и грамотно выражать свои мысли с применением математической терминологии и символики, проводить логические обоснования, доказательства математических утверждений;

  • формирование систематических знаний о плоских фигурах и их свойствах, представлений о пространственных телах;

  • формирование представлений о статистических закономерностях в реальном мире, о простейших вероятностных моделях;

  • развитие умений извлекать информацию, представленную в таблицах, на диаграммах, графиках и анализировать ее.

Общая характеристика курса математики в 5 – 6 классах

Содержание математического образования в основной школе формируется на основе фундаментального ядра школьного математического образования. В программе оно представлено в виде совокупности содержательных разделов, конкретизирующих соответствующие блоки фундаментального ядра применительно к основной школе. Программа регламентирует объём материала, обязательного для изучения в основной школе, а также даёт его распределением между 5 и 6 классами.

В данной программе курс 5-6 классов представлен как арифметико-геометрический с включением элементов алгебры. Кроме того, к нему отнесено начало изучения вероятно-статистической линии, а также элементов раздела «Логика и множества», возможность чего предусмотрена Примерной программой по математике для 5-9 классов.

Содержание раздела «Арифметика» служит базой для дальнейшего изучения математики и смежных предметов, способствует развитию логического мышления учащихся, формированию умения пользоваться алгоритмами, а также приобретению практических навыков, необходимых в повседневной жизни. При изучении арифметики формирование теоретических знаний сочетается с развитием вычислительной культуры, которая актуальна и при наличии вычислительной техники, в частности, с обучением простейшим приёмам прикидки и оценки результатов вычислений. Развитие понятия о числе связано с изучением рациональных чисел: натуральных чисел, обыкновенных и десятичных дробей, положительных и отрицательных чисел. Параллельно на доступном для учащихся данного возраста уровне в курсе представлена научная идея – расширение понятия числа.

В задачи изучения раздела «Геометрия» входит развитие геометрических представлений учащихся, образного мышления, пространственного воображения, изобразительных умений. Этот этап изучения геометрии осуществляется на наглядно-практическом уровне, при этом большая роль отводится опыту, эксперименту. Учащиеся знакомятся с геометрическими фигурами и базовыми конфигурациями, овладевают некоторыми приёмами построения, открывают их свойства, применяют эти свойства при решении задач конструктивного и вычислительного характера.

Изучение раздела «Алгебра» в основной школе предполагает, прежде всего, овладение формальным аппарата буквенного исчисления. Этот материал более высокого, нежели арифметика уровня абстракции. Его изучение решает целый ряд задач методологического, мировоззренческого, личностного характера, но и в то же время требует определённого уровня интеллектуального развития. Поэтому в курсе 5-6 классов представлены только начальные, базовые алгебраические понятия, и они играют роль своего рода мостика между арифметикой и алгеброй, назначение которого можно образно описать так: от чисел к буквам.

Изучение раздела «Вероятность и статистика» вносит существенный вклад в осознание учащимися прикладного и практического значения математики. В задачи его изучения входит формирование умения воспринимать и критически анализировать информацию, представленную в различных формах, понимать вероятный характер многих реальных зависимостей, оценивать вероятность наступления события. Для курса 5-6 классов выделены следующие вопросы: формирование умений работать с информацией, представленной в форме таблиц и диаграмм, первоначальных знаний о приёмах сбора представления информации, первое знакомство с комбинаторикой, решение комбинаторных задач.

Введение в курс элементарных теоретико-множественных понятий и соответствующей символики способствует обогащению математического языка школьников, формированию умения точно и сжато формулировать математические предложения, помогает обобщению и систематизации знаний.

В содержание основного общего образования, предусмотренного Примерными программами по математике для 5-9 классов, включён также раздел «Математика в историческом развитии». Его элементы представлены и в содержании курса 5-6 классов. Назначение этого материала состоит в создании гуманитарного, культурно-исторического фона при рассмотрении проблематики основного содержания.

Роль математики в достижение целей основного общего образования

Математическое образование играет роль в практической и духовной жизни общества.

  • Практическая сторона связана с формированием способов деятельности

  • Духовная – с интеллектуальным развитием человека, формированием характера и общей культуры.

Практическая полезность математики обусловлена тем, что её предметом являются фундаментальные структуры реального мира: пространственные формы и количественные отношения – от простейших, усваиваемых в непосредственном опыте до достаточно сложных, необходимых для развития научных и технологических идей. Каждому человеку в своей жизни приходится выполнять расчеты, находить в справочниках нужные формулы и применять их, владеть практическими приёмами геометрических измерений и построений, читать информацию, представленную в виде таблиц, диаграмм, графиков, понимать вероятностный характер случайных событий, составлять алгоритмы и др.

В школе математика служит опорным предметом для изучения смежных дисциплин. Всё больше специальностей, где необходим высокий уровень образования, связанный с непосредственным применением математики (экономика, бизнес, финансы, физика, химия, техника, информатика, биология, психология и др.).

В процессе школьной математической деятельности происходит овладение такими мыслительными операциями как индукция, дедукция, обобщение и конкретизация, анализ и синтез, классификация и систематизация, абстрагирование и аналогия. Объекты математических умозаключений и правила их конструирование вскрывают механизм логических построений, вырабатывают умение формулировать, обосновывать и доказывать суждения, тем самым развивают логическое мышление. Ведущая роль принадлежит математике в формировании алгоритмического мышления и воспитании умения действовать по заданному алгоритму и конструировать новые. В ходже решения задач – основной учебной деятельности на уроках математики – развиваются творческая и прикладная стороны мышления.

Обучение математике даёт возможность развивать у учащихся точную, экономную и информативную речь, умение отбирать наиболее подходящие языковые (в частности, символические, графические) средства.

Математическое образование вносит свой вклад в формирование общей культуры человека. Необходимым компонентом культуры в современном толковании является общее знакомство с методами познания действительности, представление о предмете и методе математики, отличие математического метода от методов естественных и гуманитарных наук, об особенностях применения математики для решения научных и прикладных задач.

История развития математического знания даёт возможность пополнить запас историко-научных знаний школьников. Знакомство с основными историческими вехами возникновения и развития математической науки, с историей великих открытий, именами людей, творивших науку, входит в интеллектуальный багаж каждого культурного человека.

Изучение математики способствует эстетическому воспитанию человека, пониманию красоты и изящества математических рассуждений, восприятию геометрических форм, усвоению идей симметрии.

Место учебного предмета в учебном плане

Базисный учебный план на изучение математики в 5 – 6-ых классах отводит 5 учебных часов в неделю в течение каждого года обучения, всего 350 часов.

Согласно Базисного образовательного плана в 5-6 классах изучается предмет интегрированный «Математика», который включает в себя арифметический материал, элементы алгебры и геометрии, а также элементы вероятностно-статистической линии.

Результаты освоения курса математики 5 – 6 классов

Личностные:

  1. знакомство с фактами, иллюстрирующими важные этапы развития математики (изобретение десятичной нумерации, обыкновенных дробей, десятичных дробей; происхождение геометрии их практических потребностей людей);

  2. способность к эмоциональному восприятию математических объектов, рассуждений, решение задач, рассматриваемых проблем;

  3. умение строить речевые конструкции (устные и письменные) с использованием изученной терминологии и символики, понимать смысл поставленной задачи, осуществлять перевод с естественного языка на математический и наоборот.

Метапредметные:

  1. умение планировать свою деятельность при решении учебных математических задач, видеть различные стратегии решения задач, осознанно выбирать способ решения;

  2. умение работать с учебным математическим текстом (выделять смысловые фрагменты, находить ответы на поставленные вопросы и пр.);

  3. умение проводить несложные доказательные рассуждения, опираясь на изученные определения, свойства, признаки; распознавать верные и неверные утверждения; опровергать с помощью контрпримеров неверные утверждения; иллюстрировать примерами изученные понятия и факты;

  4. умение действовать в соответствии с предложенным алгоритмом, составлять несложные алгоритмы вычислений и построений;

  5. применение приёмов самоконтроля при решении учебных задач;

  6. умение видеть математическую задачу в несложных практических ситуациях.

Предметные:

  1. владение базовым понятийным аппаратом по основным разделам содержания;

  2. владение навыками вычислений с натуральными числами, обыкновенными и десятичными дробями, положительными и отрицательными числами;

  3. умение решать текстовые задачи арифметическим способом, используя различные способы рассуждения;

  4. усвоение на наглядном уровне знаний о свойствах плоских и пространственных фигур; приобретение навыков их изображения; умение использовать геометрический язык для описания предметов окружающего мира;

  5. приобретение опыта измерения длин отрезков, величин углов, вычисления площадей и объёмов; понимание идеи измерения длин, площадей, объёмов;

  6. знакомство с идеями равенства фигур, симметрии; умение распознавать и изображать равные и симметричные фигуры;

  7. умение проводить несложные практические расчёты (вычисления с процентами, выполнение измерений, использование прикидки и оценки);

  8. использование букв для записи общих утверждений, формул, выражений, уравнений; умение оперировать понятием «буквенное выражение», осуществлять элементарную деятельность, связанную с понятием «уравнение»;

  9. знакомство с координатами на прямой и на плоскости, построение точек и фигур на координатной плоскости;

  10. понимание и использование информации, представленной в форме таблицы, столбчатой или круговой диаграммы;

  11. умение решать простейшие комбинаторные задачи перебором возможных вариантов.

Содержание курса математики 5-6 классов

Разделы учебной программы и характеристика основных содержательных линий

Арифметика (213 ч)

5 класс

Натуральные числа (54 ч)

Натуральный ряд. Десятичная система счисления. Арифметические действия с натуральными числами. Свойства арифметических действий.

Степень с натуральным показателем.

Делители и кратные. Свойства и признаки делимости. Простые и составные числа. Разложение натурального числа на простые множители. Деление с остатком. Числовые выражения, значение числового выражения. Порядок действий в числовом выражении, использование скобок. Решение текстовых задач арифметическим способом.

Дроби (54 ч)

Обыкновенная дробь. Основное свойство дроби. Сравнение обыкновенных дробей. Арифметические действия с обыкновенными дробями. Нахождение части от целого и целого по его части. Решение текстовых задач арифметическим способом.

Измерения, приближения, оценки (8ч)

Единицы измерения длины, площади, объема, массы, времени, скорости. Приближенное значение величины. Округление натуральных чисел.

6 класс

Дроби (69 ч)

Десятичная дробь. Сравнение десятичных дробей. Арифметические действия с десятичными дробями. Представление десятичной дроби в виде обыкновенной дроби и обыкновенной в виде десятичной.

Проценты; нахождение процента от величины и величины по ее проценту. Отношение; выражение отношения в процентах.

Рациональные числа (26 ч)

Положительные и отрицательные числа, модуль числа. Множество целых чисел. Множество рациональных чисел; рациональное число как отношение 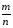, где m – целое число, n – натуральное. Сравнение рациональных чисел. Арифметические действия с рациональными числами. Свойства арифметических действий.

Координатная прямая; изображение чисел точками координатной прямой.

Измерения, приближения, оценки (2ч)

Округление десятичных дробей

Элементы алгебры (19 ч)

6 класс

Использование букв для обозначения, для записи свойств арифметических действий. Буквенные выражения. Числовое значение буквенного выражения. Допустимые значения букв в выражении.

Уравнение; корень уравнения. Нахождение неизвестных компонентов арифметических действий. Примеры решения текстовых задач с помощью уравнений.

Декартовы координаты на плоскости. Построение точки по ее координатам, определение координат точки на плоскости.

Описательная статистика. Комбинаторика (18 ч)

5 класс (12 ч)

Представление данных в виде таблиц, диаграмм.Решение комбинаторных задач перебором вариантов.

6 класс (6 ч)

Столбчатые и круговые диаграммы. Решение комбинаторных задач

Наглядная геометрия (66 ч)

5 класс (33 ч)

Наглядные представления о фигурах на плоскости: прямая, отрезок, луч, угол, ломаная, многоугольник, окружность, круг. Четырехугольник, прямоугольник, квадрат. Треугольник, виды треугольников.

Длина отрезка, ломаной. Периметр многоугольника. Единицы измерения длины. Измерение длины отрезка, построение отрезка заданной длины.

Виды углов. Градусная мера угла. Измерение и построение углов с помощью транспортира. Биссектриса угла.

Понятие площади фигуры, единицы измерения площади. Площадь прямоугольника, квадрата.

Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многоугольники. Примеры разверток многогранников, цилиндра и конуса.

Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба.

6 класс (33 ч)

Правильные многоугольники. Изображение геометрических фигур. Взаимное расположение двух прямых, двух окружностей, прямой и окружности.

Приближенное измерение площади фигур на клетчатой бумаге. Равновеликие фигуры.

Понятие о равенстве фигур. Центральная, осевая и зеркальная симметрии. Изображение симметричных фигур.

Логика и множества (4 ч)

6 класс (4 ч)

Множество, элемент множества. Задание множества перечислением элементов, характеристическим свойством. Стандартные обозначения числовых множеств. Пустое множество и его обозначение. Подмножество. Объединение и пересечение множеств.

Иллюстрация отношений между множествами с помощью диаграмм Эйлера-Венна.

Пример и контрпример.
Повторение

5 класс 9 ч

6 класс 11 ч

Планируемые предметные результаты освоения учебного курса

В результате изучения темы «Линии» обучающиеся

должны уметь:

  • Различать виды линий;

  • Проводить и обозначать прямую, луч, отрезок, ломаную;

  • Строить отрезок заданной длины и находить длину отрезка;

  • Распознавать окружность; проводить окружность заданного радиуса;

Переходить от одних единиц измерения длины к другим единицам, выбирать подходящие единицы измерения в зависимости от контекста задачи.

получат возможность:

  • Приобрести опыт выполнения проектных работ по темам: «Старинные меры длины», «Инструменты для измерения длин», «Окружности в народном прикладном искусстве».

В результате изучения темы «Натуральные числа» обучающиеся

должны уметь:

  • Понимать особенности десятичной системы счисления; знать названия разрядов и классов (в том числе «миллион»и «миллиард»);

  • Читать и записывать натуральные числа ,используя также и сокращённые обозначения (тыс., млн, млрд); уметь представлять натуральное число в виде суммы разрядных слагаемых;

  • Приобрести опыт чтения чисел, записанных римскими цифрами, используя в качестве справочного материала таблицу значений таких цифр, как L,C,D,M; читать и записывать римскими цифрами числа в простейших, наиболее употребительных случаях (например IV,XII,XIX);

  • Сравнивать и упорядочивать натуральные числа, используя для записи результата знаки и ; читать и записывать двойные неравенства;

  • Изображать натуральные числа точками на координатной прямой; понимать и уметь читать записи типа А(3);

  • Округлять натуральные числа до указанного разряда, поясняя при этом свои действия;

  • Знать термины «приближённое значение с недостатком» и «приближённое значение с избытком»;

  • Приобрести первоначальный опыт решения комбинаторных задач методом перебора всех возможных вариантов.

получат возможность:

  • познакомиться с позиционными системами счисления

  • углубить и развить представления о натуральных числах

  • приобрести привычку контролировать вычисления

В результате изучения темы «Действия с натуральными числами» обучающиеся

должны:

  • Выполнять арифметические действия с натуральными числами, находить значения числовых выражений, устанавливая порядок выполнения действий;

  • Знать, как связаны между собой действия сложения и вычитания, умножения и деления; знать термины «слагаемое», «вычитаемое», «делимое» и пр., находить неизвестное число в равенстве на основе зависимости между компонентами действий;

  • Представлять произведение нескольких равных множителей в виде степени с натуральным показателем; знать термины «степень числа», «основание степени», «показатель степени»; возводить натуральное число в натуральную степень;

  • Решать несложные текстовые задачи арифметическим методом;

  • Решать несложные текстовые задачи на движение двух объектов навстречу друг другу, на движение реке.

получат возможность:

  • углубить и развить представления о свойствах делимости натуральных чисел

  • научиться использовать приемы, рационализирующие вычисления, приобрести привычку контролировать вычисления, выбирая подходящий для ситуации способ;

  • ощутить гармонию чисел, подметить различные числовые закономерности, провести математическое исследование.

В результате изучения темы «Использование свойств действий при вычислениях» обучающиеся должны:

  • Знать и уметь записывать с помощью букв переместительное и сочетательное свойства сложения и умножения, распределительное свойство умножения относительно сложения;

  • В несложных случаях использовать рассмотренные свойства для преобразования числовых выражений: группировать слагаемые в сумме и множители в произведении; с помощью распределительного свойства раскрывать скобки в произведении и выносить в сумме общий множитель за скобки; выполняя преобразование выражения, записывать соответствующую цепочку равенств;

  • Решать арифметическим способом несложные задачи на части и на уравнение.

получат возможность:

  • Познакомиться с приемами рационализирующими вычисления и научиться использовать их;

  • Приобрести навыки исследовательской работы.

В результате изучения темы «Углы и многоугольники» обучающиеся

должны уметь:

  • Распознавать углы; использовать терминологию, связанную с углами: вершина, сторона, биссектриса;

  • Распознавать острые, тупые, прямые, развёрнутые углы;

  • Измерять величину угла с помощью транспортира и строить угол заданной величины;

  • Строить биссектрису угла с помощью транспортира;

  • Распознавать многоугольники; использовать терминологию, связанную с многоугольниками: вершина, сторона, угол, диагональ; применять классификацию многоугольников;

  • Изображать многоугольники с заданными свойствами; разбивать многоугольник на заданные многоугольники;

  • Вычислять периметр многоугольника.

получат возможность:

  • Приобрести опыт выполнения проектных работ по темам: «Геометрия циферблата часов со стрелками», «Многоугольники в окружающем мире».

В результате изучения темы «Делимость чисел» обучающиеся

должны уметь:

  • Владеть понятиями «делитель» и «кратное», понимать взаимосвязь между ними, уметь употреблять их в речи;

  • Понимать обозначения НОД (a;b) и НОК(a;b), уметь находить НОД и НОК в не сложных случаях;

  • Знать определение простого числа, уметь приводить примеры простых и составных чисел, знать некоторые элементарные сведения о простых числах .

получат возможность:

В результате изучения темы «Треугольники и четырехугольники» обучающиеся

должны:

  • Распознавать и изображать остроугольные, тупоугольные, прямоугольные треугольники;

  • Распознавать равнобедренный треугольник и использовать связанную с ним терминологию: боковые стороны, основание; распознавать равносторонний треугольник;

  • Строить равнобедренный треугольник по боковым сторонам и углу между ними; понимать свойство равенства углов при основании равнобедренного треугольника;

  • Строить прямоугольник на нелинованной бумаге с помощью чертежных инструментов;

  • Понимать свойства диагоналей прямоугольника; распознавать треугольники, получаемые при разбиением прямоугольника его диагоналями;

  • Распознавать, моделировать и изображать равные фигуры;

  • Изображать многоугольники с заданными свойствами; разбивать многоугольник на заданные многоугольники;

  • Вычислять периметр треугольника, прямоугольника, площадь прямоугольника; применять единицы измерения площади.

получат возможность:

  • Научиться вычислять площади фигур, составленных из двух и более прямоугольников;

  • Приобрести навыки исследовательской работы.

  • Приобрести опыт выполнения проектных работ по темам: «Периметр и площадь школьного участка», « План школьной территории».

В результате изучения темы «Дроби» обучающиеся

должны уметь:

  • Знать, что означают знаменатель и числитель дроби, уметь читать и записывать дроби, иллюстрировать дробь как долю целого на рисунках и чертежах;

  • Находить дробь от величины, опираясь на содержательный смысл понятия дроби;

  • Соотносить дроби и точки координатной прямой;

  • Понимать, в чём заключается основное свойство дроби, иллюстрировать равенство дробей с помощью рисунков и чертежей, с помощью координатной прямой;

  • Сокращать дроби, приводить дроби к новому знаменателю, к общему знаменателю, сравнивать и упорядочивать дроби;

  • Записывать в виде дроби частное двух натуральных чисел, представлять натуральное число в виде дроби.

получат возможность:

  • Развить и углубить знания о числе (обыкновенные дроби)

В результате изучения темы «Действия с дробями» обучающиеся

должны уметь:

  • Знать и записывать с помощью букв правила сложения и вычитания дробей с одинаковыми знаменателями; выполнять сложение и вычитание дробей с одинаковыми и с разными знаменателями;

  • Владеть приёмами выделения целой части из неправильной дроби и представления смешанной дроби в виде неправильной;

  • Знать и записывать с помощью букв правила умножения и деления дробей; применять правила на практике, включая случаи действий с натуральными числами и смешанными дробями;

  • Владеть приёмами решения задач на нахождение части целого и целого по его части;

  • Решать знакомые текстовые задачи, содержащие дробные данные.

получат возможность:

  • Научиться выполнять оценку и прикидку результатов арифметических действий с дробными числами.

В результате изучения темы «Многогранники» обучающиеся

должны:

  • Распознавать цилиндр, конус , шар;

  • Распознавать многогранники; использовать терминологию, связанную с многогранниками: вершина, ребро, грань; читать проекционное изображение многогранника;

  • Распознавать параллелепипед, изображать его на бумаге в клетку, определять измерения; распознавать и называть пирамиду;

  • Распознавать развертку куба; моделировать куб из его развертки.

получат возможность:

  • Приобрести опыт выполнения проектных работ по темам: «Модели многогранников», «Объем классной комнаты», «Макет домика для щенка», «Многогранники в архитектуре».

  • Развития пространственного воображения

  • Углубить и развить представления о пространственных геометрических фигурах.

В результате изучения темы «Таблицы и диаграммы» обучающиеся

должны уметь:

  • Анализировать готовые таблицы и диаграммы, отвечать на поставленные вопросы, делать простейшие выводы из представленных данных;

  • Заполнять несложные таблицы, следуя инструкции.

получат возможность:

  • Получить некоторое представление о методике проведения опроса общественного мнения.


Система оценки планируемых результатов

Для оценки предметных учебных достижений обучающихся используется:

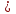  1. Входной контроль в виде диагностических административных срезов.

  2. Текущий контроль в виде самостоятельных работ.

  1   2   3   4   5   6   7