Главная страница
Анализ
Анкета
архив
Биография
Бюллетень
Викторина
Глава
Диплом
Доклад
Документация
Задача

Ashtoria.ru/catalog/shtory-kuhnya/

Как правильно выбрать шторы на кухню ashtoria.ru/catalog/shtory-kuhnya/.

ashtoria.ru


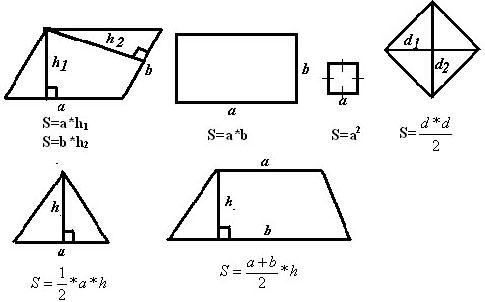
"Площади" в курсе геометрии 8-го класса включает изучение вопросов



Скачать 72.27 Kb.
Название"Площади" в курсе геометрии 8-го класса включает изучение вопросов
Дата05.04.2016
Размер72.27 Kb.
ТипУрок

Урок геометрии в 8 классе по теме:

"Площади фигур. Теорема Пифагора"



МБОУ СОШ № 5

УЧИТЕЛЬ МАТЕМАТИКИ

СИДЬКО СВЕТЛАНА НИКОЛАЕВНА

г. Лермонтов 2015 г.

Урок геометрии в 8 классе по теме: "Площади фигур. Теорема Пифагора"



Тема: “Площади” в курсе геометрии 8-го класса включает изучение вопросов:

  1. “Площадь треугольника”

  2. “Площадь параллелограмма”

  3. “Площадь трапеции”

  4. “Теорема Пифагора”

Основная цель: создать условия для формирования учащимися понятия площади, развития умений вычислять площади фигур, применяя изученные свойства и формулы, а также теорему Пифагора.

Данный урок – обобщающий по теме “Площади” и “Теорема Пифагора”, проводится для отработки навыков применения формул при вычислении площадей фигур, нахождении неизвестных сторон и высот плоских фигур.

Урок разработан на основе программы и УМК учебника “Геометрия 7-9” авторов Л. С. Атанасян, В. Ф. Бутузов, и других на основе применения технологии И. С. Якиманской.

Представленная разработка соответствует содержанию, целям и задачам геометрии указанной теме урока. Предложенный урок обобщающий, он обобщает, структурирует и систематизирует ЗУНы по теме “Площади плоских фигур. Теорема Пифагора”. Развивает геометрические представления, унифицирует систему определения площадей геометрических фигур.

Предлагаемые формы, приёмы и методы работы используемые средства обучения логически последовательны, адекватны содержанию, разнообразны, имеют аргументированную мотивацию, позволяют учащимся выбрать уровень сложности контроля самостоятельной работы сообразно личностных качеств, уровня ЗУНов, что позволяет создавать комфортную творческую обстановку в процессе учебных коммуникаций на протяжении всего урока. Такая организация урока способствует продуктивному решению познавательных учебных и личностных задач, отслеживать динамику личностного продвижения.

Диалогический характер обучения, основанный на технологии ЛОСО И. С. Якиманской, формирует гуманистические начала, развивает гуманитарное и математическое мышление, логику учащихся, учит само – и взаимооценке учебных достижений, что помогает максимально избегать возможных пробелов усвоении знаний.

Большой объем, рассмотренного на уроке учебного материала, подтверждает не только его разнохарактерную и многосложную насыщенность урока его плотность, хорошей темы, качество подготовки учащихся.

Цель урока: создать условия для

  • закрепления знаний, умения и навыков учащихся по теме “Площади”,

  • совершенствования навыков решения задач на применение теоремы Пифагора,

  • обобщения и систематизации теоретических знаний учащихся по теме “Площади” и “Теорема Пифагора”,

  • обобщение понятий: теорема Пифагора; основание, высота, диагонали.

Оборудование урока:

  1. Плакат “Площади” (Рисунок 1);


  2. Теоретический тест в двух вариантах;

  3. Карточки с готовыми чертежами к задачам (устная работа);

  4. Конверты с задачами для самостоятельной работы (индивидуальные).

Тип урока: повторительно-обобщающий.

Оргформа: урок-практикум.

Ход урока

I. Организационный момент


  • совместно с учащимися формулируем тему урока;

  • совместно с учащимися ставим задачи урока;

  • определяем основные этапы урока, для этого обратиться к учащимся с вопросами:
    какую тему мы изучили?
    что нужно знать по темам “Площади”, теорема Пифагора?
    каким образом это можно закрепить?

II. Проверка знаний учащихся


1. Проверка теории (учащиеся получают тест).

Вариант 1.

Выбери верные утверждения:

а) Площадь параллелограмма равна:

  1. произведению его сторон;

  2. произведению его высот;

  3. произведению его стороны на высоту, проведенную к данной стороне.

б) Площадь квадрата со стороной 3см равна:

  1. 6 см2;

  2. 8 см;

  3. 9 см2.

в) Закончите предложение: “Площадь ромба равна…

  1. произведению его сторон;

  2. половине произведения его диагоналей;

  3. произведению его стороны и высоты.

г) По формуле можно вычислить:

  1. площадь треугольника;

  2. площадь прямоугольника;

  3. площадь параллелограмма.

д) Площадь трапеции АВСД с основаниями АВ и СД и высотой ВО вычисляется по формуле: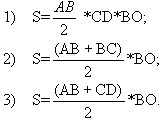



е) Теорема Пифагора утверждает, что в прямоугольном треугольнике:

  1. квадрат гипотенузы равен квадрату катета;

  2. квадрат гипотенузы равен сумме квадратов катетов;

  3. сумма квадратов катетов равна гипотенузе.

Вариант 2.

Выберите верные утверждения:

а) Площадь квадрата равна:

  1. произведению его сторон;

  2. квадрату его стороны;

  3. произведению его сторон на высоту.

б) Площадь параллелограмма равна:

  1. произведению его смежных сторон;

  2. произведению его высоты на сторону;

  3. произведению его основания на высоту, проведенную к данному основанию.

в) По формуле S=d*d /2 можно вычислить площадь:

  1. ромба;

  2. треугольника;

  3. параллелограмма.

г) Площадь треугольника равна половине произведения:

  1. оснований;

  2. основания на высоту, проведенную к данному основанию;

  3. его высот.

д) Площадь трапеции АВСД с основаниями ВС и АД и высотой ВН равна

  1. S=(AB+CD)/2*BH;

  2. S=(AD+BC)/2/BH;

  3. S=(BC+AD)/2*BH.

е) Теорема Пифагора утверждает, что в прямоугольном треугольнике:

  1. квадрат катета равен квадрату гипотенузы;

  2. квадрат гипотенузы равен сумме квадратов катетов;

  3. сумма квадратов катетов равна гипотенузе.

Учащиеся ставят знак + в выбранном ответе. По таблице ответов проводят взаимоконтроль в парах.

Таблица ответов:

вар.
а
б
в
г
д
е

1
3
3
2
1
3
2

2
2
3
1
2
3
2

2. Решение задач по готовым чертежам.

а) Решите устно, найдите площади фигур: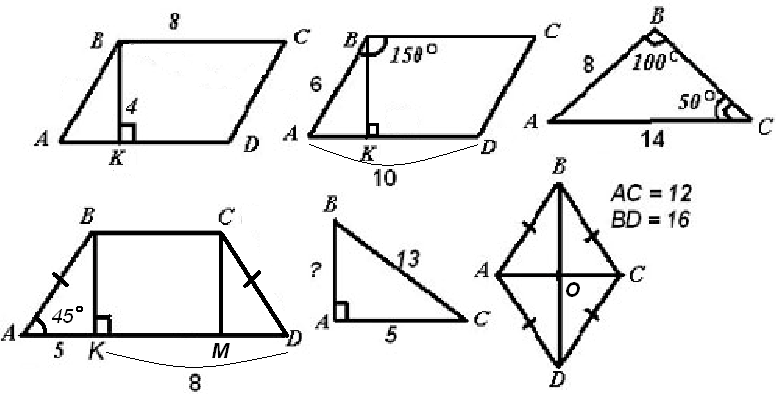



3. Решение задач письменно в тетрадях с последующей самопроверкой (по вариантам)

Вариант 1.

Дано: АВСD – трапеция; ВС : АD = 2 : 3; ВК = 6; SABCD = 60. Найти: BC, AD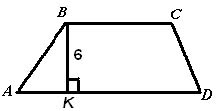



Вариант 2.

Дано: ABC; A = C = 75°; АВ = 12. Найти: SABC



Ответы:

  • Вариант 1 ВС=8, AD=12;

  • Вариант-2 SABC=36


4. Самостоятельная работа. (Каждый учащийся получает конверт с задачами 2-х уровней и сам выбирает задание на основе своего уровня подготовки).

Критерий оценки:

  • 1 уровень – “3” - №1; “4” - №1, №2.

  • 2 уровень – “4” - №1; “5” - №1, №2.

1 уровень

Вариант 1

Вариант 2

1. Диагонали ромба 12 см и 16 см. Найти сторону ромба.
1. Стороны прямоугольника 5 см и 12 см. Найти диагональ прямоугольника.

2. Боковая сторона равнобедренного треугольника равна 13 см, а основание 10 см. Найдите высоту, проведенную к основанию и площадь этого треугольника.
2. Боковая сторона равнобедренного треугольника равна 26 см, а высота, проведенная к основанию равна 24 см. Найдите основание и площадь этого треугольника.

2 уровень

1. В прямоугольной трапеции основания равны 19 см и 4 см, а большая боковая сторона 25 см. Найти площадь трапеции.
1. В прямоугольной трапеции боковые стороны равны 15 см и 9 см, а большее основание 20 см. Найти площадь трапеции.

2. Высоты параллелограмма равны 4 см и 8см, а периметр равен 36 см. Найти площадь параллелограмма.


2. Диагонали ромба равны 18 и 24 см. Найти периметр ромба и расстояние между параллельными сторонами.

Взаимопроверка работ в парах (готовое решение на доске). (См. Приложение 1).

III. Рефлексия (подведение итогов урока)


  1. Чему вы научились при изучении темы раздела;

  2. Какими навыками, умениями овладели;

  3. Какими формулами, понятиями воспользовались при решении задач?

  4. Решение каких задач показалось вам сложным?

  5. Какие вопросы требуется вашего особого внимания?

  6. Какие задачи вам понравилось решать?

IV. Домашнее задание


  • № 503; 518 (а).

  • Дополнительная задача*

*В равнобедренной трапеции со взаимно перпендикулярными диагоналями боковая сторона равна 26 см. Высота, проведенная из вершины тупого угла, делит большее основание на отрезки, меньший из которых 10 см. Найти площадь трапеции.