Мбоу новодмитриевская сош «Рекомендована»
 Скачать 0.59 Mb. Скачать 0.59 Mb.
|
ТРЕБОВАНИЯ К УРОВНЮ ПОДГОТОВКИ ВЫПУСКНИКОВВ результате изучения математики на базовом уровне ученик должен знать/понимать
Алгебра уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Функции и графики уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Начала математического анализа уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Уравнения и неравенства уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
КОНТРОЛЬ РЕАЛИЗАЦИИ ПРОГРАММЫ Стартовый контроль: 1. Записать в виде десятичной дроби: а)  ; б) ; б)  . . 2. Записать в виде обыкновенной дроби: а) 0,84; б) 5,01(6). 3. Упростить: а) 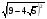 ; б) ; б) 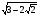 ; в) ; в) 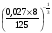 . . 4. Решить уравнение: а) 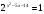 ; б) ; б)  ; в) ; в) 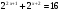 . .5. Решить неравенство: а) 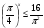 ; б) 2х – 2х-4 < 15. ; б) 2х – 2х-4 < 15. 6. Вычислить: а) 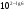 ; б) ; б) 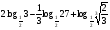 . . 7. Решить уравнение: а)  ; в) ; в)  ; ; б) log5log4log2x = 0; г) log4(x+3) – log4(x–1) = 2 – log48. 8. Решить неравенство: а)  ; б) ; б) 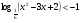 . . 9. Решить уравнение: а) 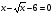 ; б) ; б) 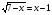 . . 10. Упростить: а) 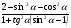 ; б) ; б) 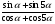 . . 11. Вычислить: а) 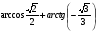 ; б) ; б)  . . 12. Решить уравнение: а) 3cos2 х + 10cos x + 3=0; б) sin2 x + 2sinx cosx = 3cos2 x. Итоговый контроль: Часть А. А1. Вычислите: 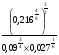 . . А2. Упростите выражение: 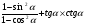 . . А3. Упростите выражение: 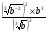 . . А4. Найдите значение выражения: 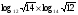 . .А5. Укажите промежуток, содержащий корень уравнения: 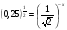 . . А6. Какому промежутку принадлежит корень уравнения: 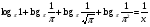 ? ? А7. Укажите множество решений неравенства: 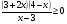 . . А8. Вычислите значение производной функции 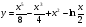 в точке х0=2. в точке х0=2. А9. Найдите область определения функции: 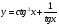 . . А10. Найдите множество значений функции: 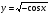 . . А11. Решите уравнение: 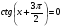 . . А12. Через точку графика функции 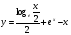 с абсциссой х0=1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс. с абсциссой х0=1 проведена касательная. Найдите тангенс угла наклона этой касательной к оси абсцисс. Часть В. Запишите решение. В1. Упростите выражение: 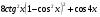 . . В2. Найдите сумму всех действительных корней уравнения: 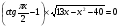 . . В3. Найдите площадь фигуры, ограниченной линиями: у = 3х(х2 – 3х + 3), у = 3х2. В4. Найдите максимальное значение функции у = log0,4(3х2 – (5а + 4)х + 49), если известно, что оно достигается в точке с абсциссой 4. Содержание учебного материала Повторение курса алгебры 10 класса – 5 часов. Основная цель – формирование представлений о целостности и непрерывности курса алгебры 10 класса, овладение умением обобщения и систематизации знаний, учащихся по основным темам курса алгебры 10 класса; развитие логического, математического мышления и интуиции, творческих способностей в области математики. Глава 1. Тригонометрические функции - 7 часов. Область определения и множество значений тригонометрических функций. Четность, нечетность, периодичность тригонометрических функций. Свойства функции y=cosх и её график. Свойства функции y=sinх и её график. Свойства функции y=tgх и её график. Обратные тригонометрические функции. Основная цель – изучить свойства тригонометрических функций, научить учащихся применять эти свойства при решении уравнений и неравенств; научить строить графики тригонометрических функций, используя различные приемы построения графиков. Среди тригонометрических формул следует особо выделить те формулы, которые непосредственно относятся к исследованию тригонометрических функций и построению их графиков. Так, формулы sin(-x)=-sin x и cos(-x)=cos x выражают свойства нечетности и четности функций y=sin x и y=cos x соответственно. Построение графиков тригонометрических функций проводится с использованием их свойств и начинается с построения графика функции y=cos x.С помощью графиков тригонометрических функций решаются простейшие тригонометрические уравнения и неравенства. На базовом уровне обратные тригонометрические функции даются в ознакомительном плане. Рекомендуется также рассмотреть графики функции y=│cos х│, y= а+cos х, y= cos (х+а), y= cos ах, y= а cos х, где а – некоторое число. Глава 2. Производная и её геометрический смысл - 13 часов. Предел последовательности. Непрерывность функции. Определение производной. Правило дифференцирования. Производная степенной функции. Производные элементарных функций. Геометрический смысл производной. Основная цель – показать учащимся целесообразность изучения производной и в дальнейшем первообразной (интеграла), так как это необходимо при решении многих практических задач, связанных с исследованием физических явлений, вычислением площадей криволинейных фигур и объемов тел с производными границами, с построением графиков функций. Прежде всего, следует показать, что функции, графиками которых являются кривые, описывают важные физические и технические процессы. Усвоение геометрического смысла производной и написание уравнения касательной к графику функции в заданной точке является обязательным для всех учащихся. Глава 3. Применение производной к исследованию функций - 11 часов. Возрастание и убывание функции. Экстремумы функции. Наибольшее и наименьшее значения функции. Производная второго порядка, выпуклость и точки перегиба. Построение графиков функций. Основная цель (базовый уровень) – является демонстрация возможностей производной в исследовании свойств функций и построении их графиков и применение производной к решению прикладных задач на оптимизацию. Глава 4 . Первообразная и интеграл - 10 часов. Первообразная. Правила нахождения первообразных. Площадь криволинейной трапеции. Интеграл и его вычисление. Применение интегралов для решения физических задач. Основная цель ознакомление учащихся с понятием первообразной и обучение нахождению площадей криволинейных трапеций. Площадь криволинейной трапеции определяется как предел интегральных сумм. Большое внимание уделяется приложениям интегрального исчисления к физическим и геометрическим задачам. Связь между первообразной и площадью криволинейной трапеции устанавливается формулой Ньютона-Лейбница. Далее возникает определенный интеграл как предел интегральной суммы; при этом формула Ньютона-Лейбница также оказывается справедливой. Таким образом, эта формула является главной: с её помощью вычисляются определенные интегралы и находятся площади криволинейных трапеций. Знакомство с простейшими дифференциальными уравнениями. Глава 5. Комбинаторика - 6 часов. Правило произведения. Размещения с повторениями. Перестановки. Размещения без повторений. Сочетания без повторений и бином Ньютона. Основная цель – ознакомление с основными формулами комбинаторики и их применением при решении задач, развивать комбинаторное мышление учащихся, ознакомить с теорией соединений, обосновать формулу бинома Ньютона. Основной при выводе формул числа перестановок и размещений является правило умножения, понимание которого формируется при решении различных прикладных задач. Свойства числа сочетаний доказываются и затем применяются при организации и исследовании треугольника Паскаля. Глава 6. Элементы теории вероятностей - 6 часов. В программу включено изучение лишь отдельных элементов теории вероятностей. При этом введению каждого понятия предшествует неформальное объяснение, раскрывающее сущность данного понятия, его происхождение и реальный смысл. Так вводятся понятия случайных, достоверных и невозможных событий, связанных с некоторым испытанием; определяются и иллюстрируются операции над событиями. Вероятность события. Сложение вероятностей. Вероятность произведения независимых событий. Основная цель – сформировать понятие вероятности случайного независимого события. Исследование простейших взаимосвязей между различными событиями, а также нахождению вероятностей видов событий через вероятности других событий. Классическое определение вероятности события с равновозможными элементарными исходами формируется строго, и на его основе (с использованием знаний комбинаторики) решается большинство задач. Понятие геометрической вероятности и статистической вероятности вводились на интуитивном уровне. При изложении материала данного раздела подчеркивается прикладное значение теории вероятностей в различных областях знаний и практической деятельности человека. Методическая литература
Для обеспечения плодотворного учебного процесса предполагается использование информации и материалов следующих Интернет – ресурсов:
|