Урок по алгебре в 10-м классе по теме "Решение простейших тригонометрических уравнений"
 Скачать 130.47 Kb. Скачать 130.47 Kb.
|
| Урок по алгебре в 10-м классе по теме "Решение простейших тригонометрических уравнений" Цели урока. Образовательные: изучить общие формулы решения простейших тригонометрических уравнений, сформировать у обучающихся первичные умения и навыки их решения; Развивающие: развивать и совершенствовать умения применять теоретические знания к решению упражнений; мыслительные способности учащихся; их речевую культуру, математический кругозор. Развивать логическое мышление, умение делать выводы и обобщения; Воспитательные: содействовать формированию личностно – адаптированой компетентности (быть подготовленным к самообразованию и самовоспитанию). Воспитывать уверенность в своих знаниях; умение слушать других; содействовать воспитанию интереса к математике; воспитывать объективность и честность при контроле знаний; культуру поведения. Тип урока: комбинированный( урок изучения нового материала.) Оборудование урока: мультимедийная аппаратура, презентация, раздаточный материал (самостоятельная работа), карточки, таблицы , листы учета знаний. Методы обучения: практический (самопроверка и взаимопроверка). Формы организации урока: индивидуальная, фронтальная, парная. Структура урока.
а) Приготовление рабочего места. Знакомство с гостями. б) Каждый оценит свою работу. (Оценочные листы) 2.Проверка домашнего задания (Взаимопроверка) 3.Устная работа 4.Психологический настрой на деятельность. Мотивация учебной деятельности. Колесо успеха 5.Изучение нового материала.
6. Отработка умений и навыков по решению простейших тригонометрических уравнений. 7.Самостоятельная работа. (Проверка первичного усвоения знаний, умений и навыков по теме)
Ход урока.
На экране слова: “Учиться можно только весело, чтобы переваривать знания, надо поглощать их с аппетитом” (Анатоль Франс (1844– 924) – французский писатель) (слайд Учитель: Следуя советам писателя, давайте будем активны, внимательны и с большим удовольствием будем поглощать знания, которые понадобятся в дальнейшем. Чтобы легче всем жилось, Чтоб решалось, чтоб моглось. Улыбнитесь! Удачи всем! Чтобы не было проблем! (слайд 2) Ребята,для нашего урока нам необходим дополнительный материалл, который лежит на вашем рабочем месте в определенном порядке.Обратите внимание. Сегодня каждый из вас оценит свою работу. Возьмите в руки рабочую карту и подпишите ее. Рабочая карта __________________________________________________________
II. Этап проверки домашнего задания а) Вычислить:  , т.к. , т.к. 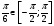 , ,  , т.к. , т.к.  , т.к. , т.к. 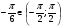 , , (Взаимопроверка) ( слайд 3,4,5) А творческую часть домашнего задания проверим мы проверим немного позже. III. Фронтальный опрос и устная работа. (кодоскоп) Вопросы: а) Дать определение: arcsin 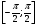 , синус которого равен а) arccos , синус которого равен а) arccos 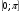 , косинус которого равен а.) , косинус которого равен а.)arctg 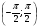 , тангенс которого равен а. , тангенс которого равен а.arcctg б) Имеют ли смысл выражения(кодоскоп) 1) arcsin 2) arсcos 3) arсcos 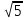 ; ;4) arcsin 1,5 ; 5) arctg 5; 6) arcсtg 7) arccos 1,8 ; 8) arcsin π. А сейчас проверим творческую часть домашнего задания lV Психологический настрой на деятельность. Мотивация учебной деятельности. Колесо успеха В итоге анкетирования мы с вами установили,что для того чтобы ощущать себя успешным,для каждого из вас необходимо либо исполнение вашей мечты или достижение какихто целей.Давайте посмотрим как мы двигаемся к своей мечте. Мы с вами условились, вся площадь этого колеса 100% . Я просила вас ответить на вопрос: Как я оцениваю свое: Здоровье, личностный и духовный рост( читаю ли я книги.расту ли я как личность), отношение с родителями, отношение с друзьями, эмоции(умею ли я владеть своими чувствами, эмоциями), отношение к учебе, подготовка к ЕГЭ .Отметили. Соединили все плавной линией. Как вам нравиться ваше колесо? Представьте,что это колесо вашей жизни.На нем вы стремитесь к успеху! Доедите далеко? Это просто упражнение. Вам есть к чему стремиться! Задумайтесь, что нужно делать изо дня в день,чтобы ближе к своей мечте. Заглядывайте в свое колесо,выравнивайте изо дня в день. Если полностью закрыли, увеличте круг! И сейчас мы будем пополнять свое колесо успеха А давайте посмотрим,где самый большой % стремление к успеху. ( Анализируем)! Тема сегоднешнего урока поможет вам в подготовке к ЕГЭ. Возьмите в руки книгу « математика» по подготовке к ЕГЭ под редакцией Ф.Ф. Лысенко. Мы с вами многие задания решаем из нее. Сейчас, я прошу обратить внимание на задание В3 варианта №26 стр.145.Это простейшее тригонометрическое уравнение. Кому из вас необходимо знать, как его решить? А теперь обратите внимание на задание С1 вариантов 1,2,3,4,5 и т.д. Решить систему тригонометрических уравнений. Эти тригонометрические уравнения не являются простейшими, но решаются они путем приведения их к простейшему виду. Хотите научиться их решать? Запишите число и тему урока "Решение простейших тригонометрических уравнений" Назвать цели урока: вывести общие формулы решения простейших тригонометрических уравнений. Все, что мы делаем нужно! Так давайте работать честно, Усердно и дружно! V. Получения новых знаний На протяжении многих уроков мы научились 1) отмечать точки на числовой окружности; 2) определять значения синуса, косинуса, тангенса и котангенса для точек числовой окружности; 3) знаем свойства основных тригонометрических функций; 4) на предыдущем уроке мы познакомились с понятием арксинуса, арккосинуса, арктангенса, арккотангенса и научились отмечать их на числовой окружности. Для чего же нам понадобились эти знания? (слайд 6) Тригонометрическими уравнениями называют уравнения, в которых переменная содержится под знаком тригонометрических функций. Для решения различных видов тригонометрических уравнений необходимо уметь решать простейшие тригонометрические уравнения. К ним относятся уравнения вида:  , , 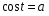 , , 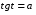 , , 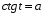 . Некоторые представления о решении таких уравнений мы уже имеем. Задача нашего урока состоит в следующем: нам необходимо вывести общие формулы для решения простейших тригонометрических уравнений. . Некоторые представления о решении таких уравнений мы уже имеем. Задача нашего урока состоит в следующем: нам необходимо вывести общие формулы для решения простейших тригонометрических уравнений.Групповая работа Алгоритм работы в группе:
Учебное исследование. Задание 1 группе.
а) 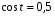 ; б) ; б) 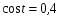 ; в) ; в) 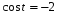 . .
Задание 2 группе.
а) 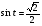 ; б) ; б) 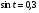 ; в) ; в) 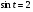 . .
Задание 3 группе.
а) 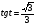 ; б) ; б) 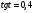 ; в) ; в) 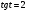 . .
Задание экспертной группе.(учитель) Представьте общие выводы решений простейших тригонометрических уравнений. Выступления от групп. Обсуждение итогов учебного исследования. Учитель: Внимательно слушайте объяснение лидера группы , фиксируйте в тетради основные моменты решения тригонометрических уравнений . 1 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 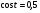 . Отметим на окружности точки М и Р с абсциссой 0,5 (она лежит на прямой х. = 0,5). Точка М соответствует числу . Отметим на окружности точки М и Р с абсциссой 0,5 (она лежит на прямой х. = 0,5). Точка М соответствует числу 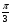 , а значит, всем числам вида , а значит, всем числам вида 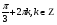 . Точка Р соответствует числу . Точка Р соответствует числу 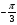 , а, следовательно, и всем числам вида , а, следовательно, и всем числам вида  . В итоге получаем две серии решений уравнения: . В итоге получаем две серии решений уравнения: 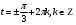 . .Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 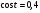 . Отметим на окружности точки М и Р с абсциссой 0,4 (она лежит на прямой х. = 0,4). Это уравнение имеет два решения, но каких мы не знаем. Наверно, необходима новая математическая формула. . Отметим на окружности точки М и Р с абсциссой 0,4 (она лежит на прямой х. = 0,4). Это уравнение имеет два решения, но каких мы не знаем. Наверно, необходима новая математическая формула.Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 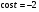 . Это уравнение не имеет решений, т.к. прямая х. = -2 не пересекает числовую окружность. . Это уравнение не имеет решений, т.к. прямая х. = -2 не пересекает числовую окружность.Вывод: уравнение 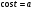 имеет две серии решений при имеет две серии решений при 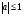 , не имеет решений при , не имеет решений при 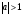 . Для решения уравнения . Для решения уравнения 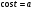 необходимо ввести новую математическую формулу. необходимо ввести новую математическую формулу.2 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 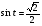 . Отметим на окружности точки М и Р с ординатой . Отметим на окружности точки М и Р с ординатой 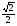 (она лежит на прямой (она лежит на прямой 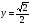 ). Точка М соответствует числу ). Точка М соответствует числу 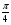 , а значит, всем числам вида , а значит, всем числам вида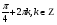 . Точка Р соответствует числу . Точка Р соответствует числу 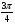 , а, следовательно, и всем числам вида , а, следовательно, и всем числам вида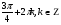 . В итоге получаем две серии решений уравнения: . В итоге получаем две серии решений уравнения:  ; ; 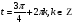 . .Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 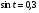 . Отметим на окружности точки М и Р с ординатой 0,3 (она лежит на прямой у = 0,3). Это уравнение имеет два решения, но каких мы не знаем. . Отметим на окружности точки М и Р с ординатой 0,3 (она лежит на прямой у = 0,3). Это уравнение имеет два решения, но каких мы не знаем. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 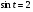 . Это уравнение не имеет решений, т.к. прямая у = 2 не пересекает числовую окружность. . Это уравнение не имеет решений, т.к. прямая у = 2 не пересекает числовую окружность.Вывод: уравнение 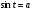 имеет две серии решений при имеет две серии решений при 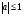 , не имеет решений при , не имеет решений при 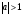 . Решение уравнения . Решение уравнения 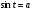 вызвало у нас затруднение. вызвало у нас затруднение.Мы считаем, что для решения уравнения 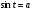 также необходимо ввести новую математическую формулу. также необходимо ввести новую математическую формулу.3 группа. Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 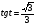 . На линии тангенсов отметим число . На линии тангенсов отметим число 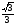 . Прямая ОТ пересекает окружность в двух точках М, Р. Точка М соответствует числу . Прямая ОТ пересекает окружность в двух точках М, Р. Точка М соответствует числу 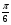 , точка Р соответствует числу - , точка Р соответствует числу -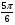 . Учитывая периодичность функции y = tgx, можно сказать, что уравнение . Учитывая периодичность функции y = tgx, можно сказать, что уравнение 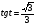 имеет одну серию решений имеет одну серию решений 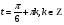 . .Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 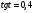 . На линии тангенсов отметим число 0,4. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . . На линии тангенсов отметим число 0,4. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . Используя геометрическую модель – числовую окружность на координатной плоскости, решим уравнение 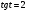 . На линии тангенсов отметим число 2. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . Наверно, здесь имеют место математические термины, которые мы изучили на прошлом уроке-это arctgа . На линии тангенсов отметим число 2. Прямая ОТ пересекает окружность в двух точках М, Р. Это уравнение имеет одну серию решений, но записать это решение мы не смогли . Наверно, здесь имеют место математические термины, которые мы изучили на прошлом уроке-это arctgаВывод: уравнение 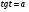 имеет одну серию решений при любом значении параметра а. Для решения уравнения имеет одну серию решений при любом значении параметра а. Для решения уравнения 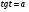 необходимо ввести новую формулу. необходимо ввести новую формулу.Учитель: Ребята,с какими же уравнениями увас возникли проблемы? 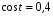 , , 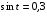 , , 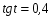 , , 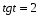 . .Итак, для решения простейших тригонометрических уравнений, были введены новые математические термины. Какие? (arcsin Презентация слайд 7-16 Если 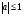 , то уравнение , то уравнение 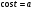 имеет решения имеет решения 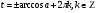 . . Если а = -1; 0; 1, то пользуются более простыми формулами: 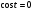 , , 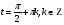 ; ; 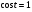 , , 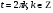 ; ; 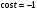 , , 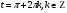 . .Если 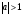 , то уравнение , то уравнение 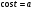 решений не имеет. решений не имеет.Если 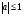 , то уравнение , то уравнение 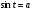 имеет две серии решений имеет две серии решений 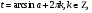 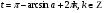 . Эти две формулы можно объединить одной формулой. Перепишем эти формулы следующим образом: . Эти две формулы можно объединить одной формулой. Перепишем эти формулы следующим образом: 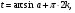 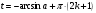 . Замечаем, что если перед arcsin a стоит знак «плюс», то у числа . Замечаем, что если перед arcsin a стоит знак «плюс», то у числа  множителем является четное число 2k. Если же перед arcsin a стоит знак «минус», то у числа множителем является четное число 2k. Если же перед arcsin a стоит знак «минус», то у числа  множителем является нечетное число 2k + 1. Это наблюдение позволяет записать общую формулу для решения уравнения множителем является нечетное число 2k + 1. Это наблюдение позволяет записать общую формулу для решения уравнения 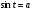 : : 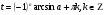 . . Если а = -1; 0; 1, то пользуются более простыми формулами: 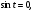 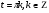 ; ; 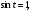 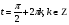 ; ; 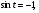 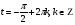 . .Если 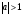 , то уравнение , то уравнение 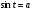 решений не имеет. решений не имеет.Уравнение 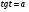 имеет решения имеет решения 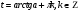 для любого значения а. для любого значения а.(Для решения уравнения 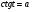 выступление аналогичное). выступление аналогичное).Схематизация материала. Представим общие формулы решения простейших тригонометрических уравнений в виде таблиц.(На доске) Vl. Отработка умений и навыков по решению простейших тригонометрических уравнений. 1)Учащиеся, пользуясь полученными формулами, решают уравнения. 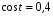 , , 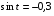 , , 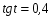 , , 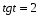 . .Решите уравнения: У доски 2 учащихся по очереди решают уравнения: слайд 17 2) 2sin х = 1, 2cosх = 3) Работа с учебником №136а- №139а, №140а,б (Решаем и коментируем с места) VI.Самостоятельная работа. (Проверки первичного усвоения знаний, умений и навыков по теме ) (разноуровневые задания по карточкам) Каждый работает индивидуально, а вместе мы подготовим следующую литературную минутку нашего урока. Кто решил показывает ответ,если он верен,выбираем по ответу слово и вывешиваем на свое место на доску Решите уравнения: 1) sinх= - 2) cosх = 1,1, 3 ) 2sinх – 1 = 0, 4) tgх =1,7. 5) cosх = 0 6) sinх = 7) 2 cosх - 2=0, Литературная минутка. В результате на доске высказывание: «Быть человеком, значит чувствовать свою ответственность» Сент-Экзюпери Ребята, мне очень хотелось вас познакомить с этой мудрой мыслью французского писателя, который в своих произведениях сумел показать доверие людей друг к другу.Нравственная сторона его произведений-вера в возможность в понимание и единение людей. Ребята, я просила подготовить о нем краткую информацию. (Он написал «Маленкий принц»-сказку «Планета людей». «Южный почтовый» и др.Советую вам почитать эти романы.Его годы жизни 1900-1944г.Он летчик,погиб на войне,в разведательном полете.) Ребята,наш урок подходит к концу,и во-первых я могу сказать вам спасибо за то,что каждый из вас чувсвовал свою ответственность. VII. Домашнее задание. Задачи: сообщить учащимся домашнее задание, дать краткий инструктаж по его выполнению. П.9, № 137-141 (г). Сборник Лысенко №146 Учащиеся записывают домашнее задание в дневники. Подведение итогов: 1)Чем занимались на уроке? 2)Что узнали нового на уроке? 5)Поставьте оценки в дневник 6)Экран настроения. Смайлики вывешиваем на доску Карточка№1 Заполни пустые клетки  | ||||||||||||||||||||||||
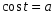 .
.