|
«Признаки делимости»
Приложение 1
Тема урока: «Признаки делимости»
Цель и задачи урока:
Создать условие для восприятия понятий признаки делимости, помочь ребятам открыть признаки делимости чисел; классифицировать признаки в простейших ситуациях; закрепить вычислительные навыки;
Начать формирование умений и навыков применения признаков делимости;
Развить мышление и элементы творческой деятельности (интуиции, смекалки, умение сравнивать, анализировать, выявлять закономерности, обобщать, конкретизировать, классифицировать);
Продолжить формирование познавательной активности деятельности, умения логически мыслить, активно рационально, работать;
Воспитание ответственного отношения к учебному труду, умения преодолевать учебные трудности, умения работать самостоятельно.
«Отыщи всему начало
и ты многое поймешь»
К. Прутков.
№
п.п
|
Деятельность учителя
|
Деятельность учащихся
|
1
|
Формулирование темы урока.
Постановка учебно-познавательной задачи.
На сегодняшнем уроке мы продолжим работу с простейшими понятиями, связанными с делимостью чисел; рассмотрим новый вопрос: «Признаки делимости». Как вы думаете, какая сегодня перед нами стоит цель?
|
Записывают тему; формулируют цель: получить в ходе работы признаки делимости.
|
2
|
Мотивационно-ориентировочный этап.
Актуализация.
Прежде, чем перейти к новой теме, давайте ответим на некоторые вопросы:
- Какое натуральное число называют делителем данного числа?
- Какое число называют кратным данному натуральному числу?
- Какое натуральное число является делителем каждого натурального числа?
- Какое число является кратным любому натуральному числу?
|
Отвечают на вопросы
|
3
|
Усвоение новых знаний и способов действий.
Запишите 10 чисел, кратных 2
Какими цифрами оканчиваются эти числа? Как они называются?
Какой вывод можно сделать?
Запишите 5 чисел, кратных 5.
Что теперь вы можете сказать?
Почему?
Запишите 5 чисел, кратных 10.
Какой вывод можно сделать?
Почему?
И так, вы открыли три признака делимости чисел: на 2, на 5, на 10. Что является общим для этих признаков?
Молодцы, хорошо. А теперь, вам предстоит из предложенных чисел:
125, 460, 195, 224, 876, 1540, 7400, 3048, 5605, 1380
выбрать, пользуясь открытыми вами признаками, те которые делятся:
а) на 2; б) на 5; в) на 10.
(взаимопроверка)
Справились с заданием хорошо.
Следующее задание:
Записать 9 чисел кратных 3.
Можно ли вопрос о делимости на 3 решить так же как в предыдущих случаях?
Запишите 5 чисел кратных 9.
Можно ли вопрос о делимости на 9 решить так же как в предыдущих случаях?
Как же нам быть? (если нет правильного ответа, или ответа близкого к правильному, то прихожу на помощь).
Давайте заполним таблицу:
Число
|
456
|
162
|
6507
|
225
|
372
|
834
|
Сумма цифр числа
(записываю не сразу)
|
15
|
9
|
18
|
9
|
12
|
15
|
Обратите внимание на сточку «сумма цифр», проверьте, делятся ли полученные числа на 3?
На 9?
Какой вывод можно сделать?
Что является общим для этих признаков?
А теперь, вам предстоит из предложенных чисел:
321, 675, 1005, 2382, 6543, 7236, 49077
Выбрать, пользуясь открытыми вами признаками, те которые делятся на:
а) на 3; б) на 9
(взаимопроверка)
|
2,4,6,8,10,12,14,16,18,20
Чётные.
Делают вывод, тем самым, формулируя признак делимости на 2.
5,10,15,20,25
Делают вывод, получая признак.
При умножении на 5 получают числа, которые оканчиваются на 0 или 5.
10,20,30,40,50
Делают вывод, получая признак делимости на 10.
При умножении на 10 получают числа, которые оканчиваются на 0.
Делимость чисел определяется по последней цифре числа.
Выполняют задание.
Проверяют друг у друга.
3,6,9,12,15,18,21,24,27
Нет.
9,18,27,36,45
Нет.
Предлагают свои идеи.
Заполняют таблицу.
Делают вывод, получая признаки деления на 3 и на 9.
Делимость чисел определяется по сумме цифр в записи числа.
Выполняют задание.
Проверяют друг у друга
|
4
|
Первичная проверка понимания изученного
У вас на столе лежат заготовки таблиц «Признаки делимости», давайте вместе с вами заполним их (см. ниже).
Пользуясь таблицей, вместо пропусков поставьте цифры так, чтобы числа
937∆, 88∆, 1234∆, 111∆, 26∆∆,
55∆∆, 83∆∆, 5∆∆
Делились на: а) 2; б) 3; в) 5; г) 10.
|
Заполняют таблицу, проговаривая признаки делимости.
Выполняют задание.
|
5
|
Задание на дом: номера из учебника;
Творческое задание: составить свои деформированные примеры.
|
Записывают задание.
|
6
|
Подведение итогов урока.
- Какие признаки делимости были открыты вами сегодня на уроке?
- На сколько групп можно разделить все рассмотренные признаки делимости?
За 2 минуты до конца урока, предлагаю заполнить лист успеваемости.
|
Отвечают на вопросы.
Заполняют и сдают.
|
Таблица Признаки делимости.
Число делиться
На
|
Если:
|
Пример
|
2
|
оно оканчивается чётной цифрой 0,2,4,6,8.
|
26 оканчивается чётной цифрой 6, оно делится на 2.
|
3
|
Сумма цифр этого числа делится на 3
|
285 2+8+5=15 делится на 3, значит число 285 делится на 3.
|
5
|
Оно оканчивается цифрой 0 или 5
|
2505 оканчивается цифрой 5, оно делится на 5.
|
9
|
Сумма цифр этого числа делится на 9
|
351 3+5+1= 9, 9 делится на 9, значит число 351 делится на 9.
|
10
|
Оно оканчивается цифрой 0
|
2850 оканчивается цифрой 0, оно делится на 10.
|
4
|
Две последние цифры этого числа образуют число, делящееся на 4
|
3164 две последние цифра составляют число 64, оно делится на 4, значит число 3164 делится на 4.
|
25
|
Оно оканчивается на 00, 25, 50, 75
|
7325 оканчивается на 25, значит оно делится на 25.
|
Тема урока: Простые и составные числа. Разложение на простые множители (фрагмент урока).
Цели и задачи урока:
Создать условие для восприятия понятий простое и составное число, помочь ребятам открыть способ разложения чисел на простые множители;
Начать формирование умений и навыков разложения на простые числа;
Продолжить формирование познавательной активности деятельности, умения логически мыслить, активно рационально, работать;
Воспитание ответственного отношения к учебному труду, умения преодолевать учебные трудности, умения работать самостоятельно.
№
п\п
|
Деятельность учителя
|
Деятельность ученика
|
1
|
Формулирование темы урока. Постановка учебно-познавательной задачи.
Тема сегодняшнего урока «Простые и составные числа. Разложение на простые множители».
Давайте вместе с вами сформулируем цели нашего урока.
|
Записывают тему; формулируют цель: в ходе работы на уроке получить способ разложения на простые множители.
|
2
|
Мотивационно-ориентировочный этап
Актуализация.
Дома вам было дано задание найти 15 чисел, которые имеют только два делителя – 1 и само число. Все справились с этим заданием?
К доске вызываются 3 ученика, которые записывают свои числа. Запись остается на доске.
|
Проверяют правильность выполнения.
|
3
|
Оперативно-исполнительский этап.
Сколько делителей имеет, записанные на доске, каждое из чисел?
Эти числа называют простыми. Попробуйте сами дать определение простому числу.
Ребята, тогда как будут называться числа, которые имеют 3 и более делителей?
Попробуйте сами дать определение составному числу.
У вас в конце учебника приведена таблица простых чисел от 2 до 997. как вы думаете, почему одни числа выделены белым цветом, а другие черным?
Два простых числа, разность которых равна 2, называются близнецами. Найдите пары таких чисел
А как вы думаете, почему в таблице простых чисел нет 1? И вообще, 1 это простое или составное число?
Задача.
Нужно выделить участок земли прямоугольной формы площадью 18 м2. какими могут быть размеры этого участка, если они должны выражаться натуральными числами?
Решая с вами задачу, что мы сделали с числом 18?
А какая у нас сегодня с вами задача? Обратите внимание на полученные числа, они простые?
Как нам тогда поступить, чтобы получились простые множители?
Тогда что у вас получится?
Что же значит разложить число на простые множители?
Давайте запишем это красиво:
2
9 3
3 3
1
И так далее.
|
Два.
Формулируют (предлагают свои варианты) определение.
Составные.
Формулируют (предлагают свои варианты) определение.
Работают с таблицей.
Предлагают свои варианты.
Предлагают свои варианты.
Делают вывод, что 1 не относится ни к простым, ни к составным числам.
Решают задачу:
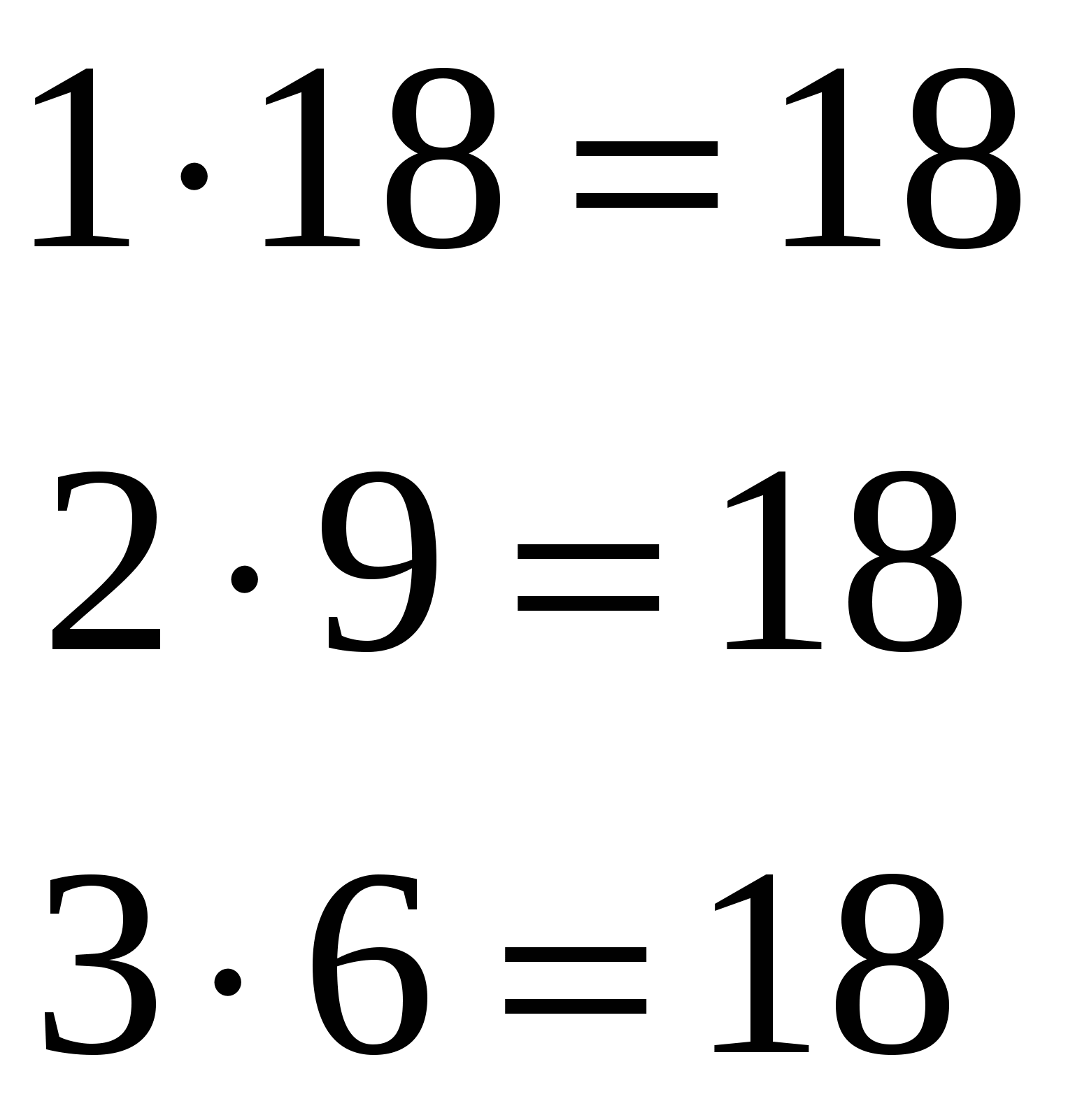
Ответ: размеры участка могут быть:1м и 18м; 2м и 9м; 3м и 6м.
Разложили на множители.
Разложение на простые множители. Нет.
Разложить составные числа на простые числа.
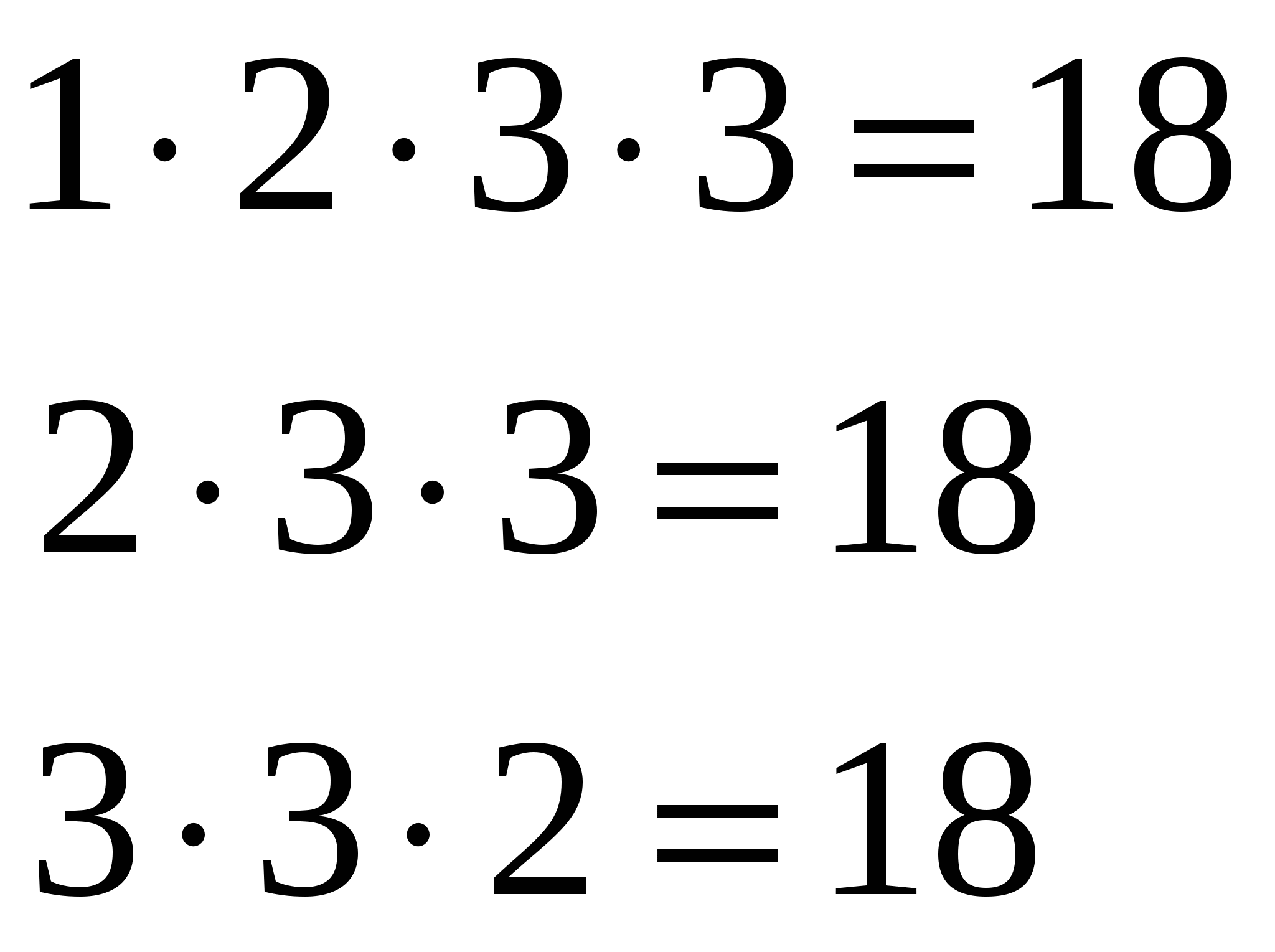
Представить это число в виде произведения простых чисел.
|
В результате работы на одном уроке мы знакомимся с понятиями простое и составное число, и показываем для чего это нам надо, и вместо того, чтобы на объяснение материала затрачивать 2 урока, мы затрачиваем один, тем самым, оставляя больше времени на практическую отработку умений и навыков
Совместное изучение тем «Наибольший общий делитель» и «Наименьшее общее кратное» экономит час учебного времени. На изучение тем в отдельности отводится 3 и 4 часа соответственно, но, рассмотрев на одном уроке понятия НОД, взаимно простые числа, НОК, на формирование и контроль умений и навыков остается 6 часов, чего вполне достаточно для хорошего усвоения тем.
Приведу фрагмент такого урока.
В начале урока, дети помогают формулировать цель и задачи урока, повторяют, что называется делителем числа и что такое кратное. Затем делим лист тетради пополам, с одной стороны записываем НОД, с другой – НОК, и выполняем работу.
НОД
|
НОК
|
Деятельность учителя
|
Деятельность ученика
|
Деятельность учителя
|
Деятельность ученика
|
Запишите через запятую все делители чисел 36 и 52
Выберете и подчеркните, то наибольшее общее число, которое является делителем и 36 и 52.
Чем является число 4 для этих чисел
Сформулируйте определение НОД.
Разложить на простые множители числа 32 и 75
Выберете числа, которые встречаются в разложении этих чисел
Оно и является
Разложите на простые множители числа 875 и 5625. выберете числа, которые встречаются в разложении этих чисел, т.е. найдите «близнеца», подчеркните их.
Найдите произведение подчеркнутых чисел, оно и будет являться НОД
Теперь пользуясь этим примером составьте алгоритм нахождения НОД,
Учитель корректирует
|
Записывают
Д(36)– 1,2,4,6,9,12,
18,36
Д(52) – 1,2,4,13,26,52
Наибольшим общим делителем.
Формулируют.
Выполняют
3  5 5 75 5 5 5 75 5
7 7 15 5
1 3 3
1
Это число 5
НОД(35;75) = 5
Выполняют
  875 5 5625 5 875 5 5625 5
175 5 1125 5
35 5 225 5
7 7 45 5
1 9 3
3 3
1
НОД(875;5625) = 15
Составляют.
1. Разложить числа на простые множители;
2. Выбрать одинаковые, т.е. числа которые встречаются в разложении этих чисел, подчеркнуть.
3. Найти произведения подчеркнутых чисел.
|
Запишите через запятую 8 чисел, которые кратны 30, а затем 10 чисел, которые кратны 24.
Выберете и подчеркните, наименьшее общее число, которое является кратным и 30 и 24.
Чем является число 120 для этих чисел?
Сформулируйте определение НОК
Разложите на простые множители числа 30 и 24
В разложении числа 24 зачеркните, те множители, которые встречаются в разложении числа 30
Выпишите разложение числа 30, и дополните теми множителями, которые остались в разложении числа 24.
Пользуясь этим примером, составьте алгоритм нахождения НОК.
Учитель корректирует
|
Записывают
К(30) – 30,60,90,120,
180,210,240
К(24) – 24,48,72,96,120,
144,168,192,216,240
Выполняют
Наименьшим общим кратным
Формулируют
Выполняют
3  0 2 24 2 0 2 24 2
15 3 12 2
5 5 6 3
1 2 2
1
Это числа 2 и 3
Выполняют
НОК(30;24) = 3 2 5 2 2 = 120
Составляют.
1.Разложить на простые множители;
2. Выписать все множители одного числа и дополнить недостающими множителями, из разложения другого числа.
3. Найти произведение этих множителей
|
Тема урока: Формула разности квадратов.
Цели и задачи урока:
Создать условия для осознанного усвоения формулы разности квадратов;
Начать формирование умения сокращенно находить произведение разности двух чисел и их суммы; разлаживать многочлен на множители, используя формулу разности квадратов;
Продолжить формирование познавательной активности деятельности, умения логически мыслить, активно рационально, работать;
Воспитание ответственного отношения к учебному труду, умения преодолевать учебные трудности, умения работать самостоятельно.
№
п\п
|
Деятельность учителя
|
Деятельность ученика
|
1.
|
Проверка домашнего задания
Выполнить умножение многочленов:
(m - n)(m + n) = m2 + mn – nm – n2 = m2 – n2;
(a + b)(a – b) = ………………. = a2 – b2;
(c + d)(d – c) = ………………. = d2 – c2;
(2a – b)(2a + b) = …………….. = 4a2 + b;
(x + y)(2x – y) = 2x2 – xy + 2xy – y2.
Каким правилом вы пользовались?
Как умножить многочлен на многочлен?
Какую операцию вы выполняли?
Актуализация опорных знаний
Работа с классом устно.
1. Возвести в квадрат произведение
(xy)2; (5a)2; (0,3a2)2; (4x2y3p)2; (0,1and4)2
Какое правило использовали?
2. Представить в виде квадрата одночлена
25,4a2, 9b2; 0,16m4; 0,81c6; 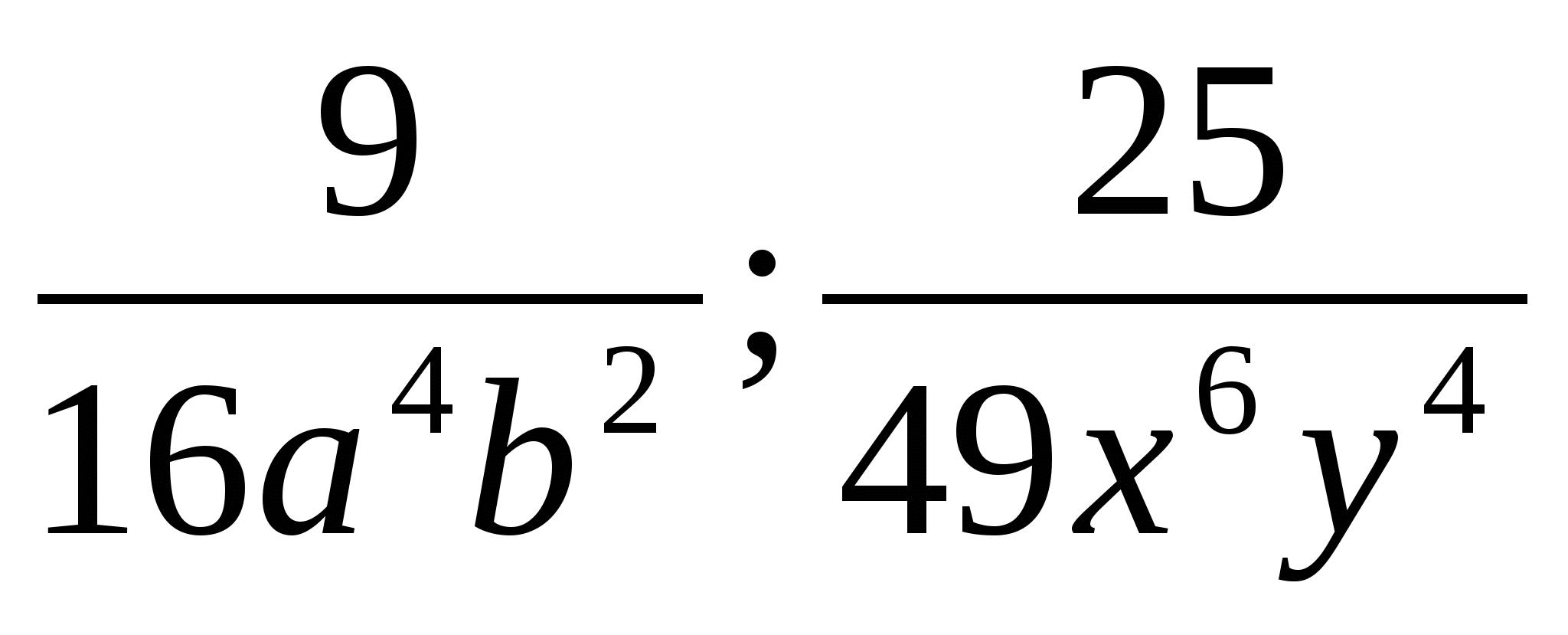 ; a12/ ; a12/
3. Прочитать выражение.
(x + y)2; x2 + y2; (x – y)2; x2 – y2;
(5a + 6b)2; (2y)2 – (3c)2
|
Проверяют
Отвечают на вопросы
Работают устно.
Отвечают на вопросы.
|
2.
|
Изучение нового материала
Внимательно посмотрите на начало записи и её конец.
(m - n)(m + n) = m2 + mn – nm – n2 = m2 – n2;
Установите, как сразу можно выполнить умножение.
Что получилось в результате?
В каком порядке расположены члены в результате?
Какова закономерность?
Любое ли произведение многочленов обладает этой закономерностью?
Запишем эту закономерность в виде формулы
(a + b)(a – b) = a2 – b2
Эта формула позволяет сокращенно умножать разность двух чисел и их сумму, поэтому её называют формулой сокращённого умножения.
Произведение разности двух чисел и их суммы равно разности квадратов этих чисел.
Эту формулу можно применять справа на лево и наоборот.
Разность квадратов двух чисел равна произведению разности этих чисел и их суммы.
Как будут называться эти операции?
 представить в виде многочлена стандартного вида представить в виде многочлена стандартного вида
(a – b) (a + b) = a2 – b2

разложить на множители
В виде a и b могут выступать различные выражения.
Что значит разложить на множители?
Какие способы разложения вы знаете?
|
Отвечают на вопросы
Записывают формулу
|
3.
|
Первичное применение знаний
1. Представить в виде многочлена стандартного вида.
(2b + a)(2b – a)
(y + 6x)(6x – y)
(3a2 + 4b3)(3a2 – 4b3)
Какую операцию вы выполняли?
2. Разложить многочлен на множители
a2 – 9; 25x2 – 16; 64y2 – 0,36x2; 81a6 – 49b4
Какую операцию вы выполняли?
3. Восстановит запись
(х - ∆)(х +∆) = х2 – y2;
(∆ - 3а)(3а +∆) = с2 –  2; 2;
(5у - ∆)(∆ + 5у) = 25у2 –4х2;
100 – х2 = (∆ - х)(∆ + х);
а2 – ∆2 = (а - 9)(а + 9).
4. Найдите ошибку
а) (3 – в)(3 + в) = 9 + в3
б) (х – 2)(х + 2) = х2 – 2
в) (в – 5а)(5а + в) = 25а2 + в2
5. Как вы думаете, где можно использовать изученную формулу сокращенного умножения?
|
Выполняют задание
Отвечают на вопросы
Выполняют
1. Представлять многочлен в стандартом виде.
2.Разложить многочлен на множители.
3. Упростить выражение
4. Решение уравнений.
| |
|
|
 Скачать 154.78 Kb.
Скачать 154.78 Kb.
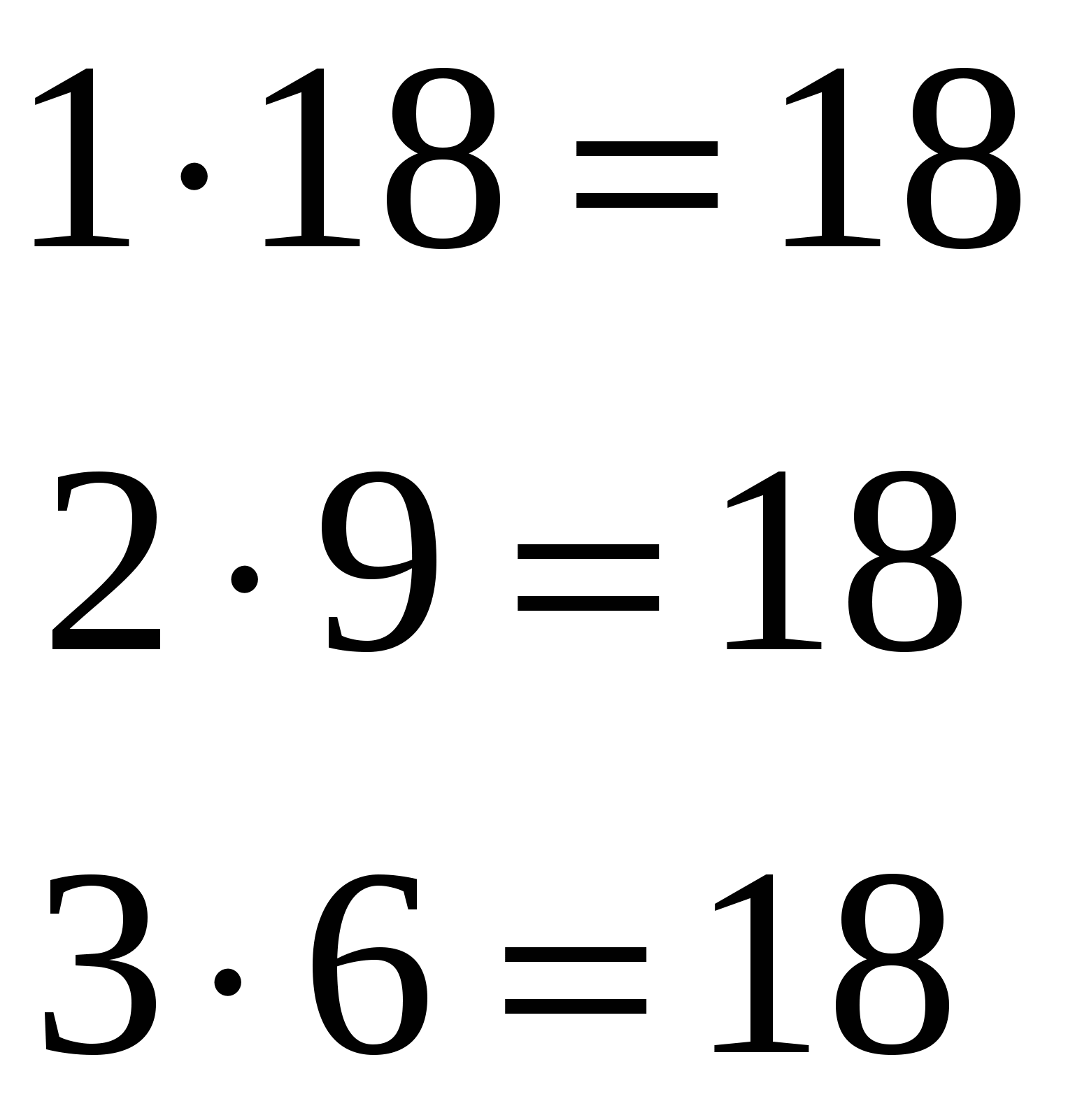
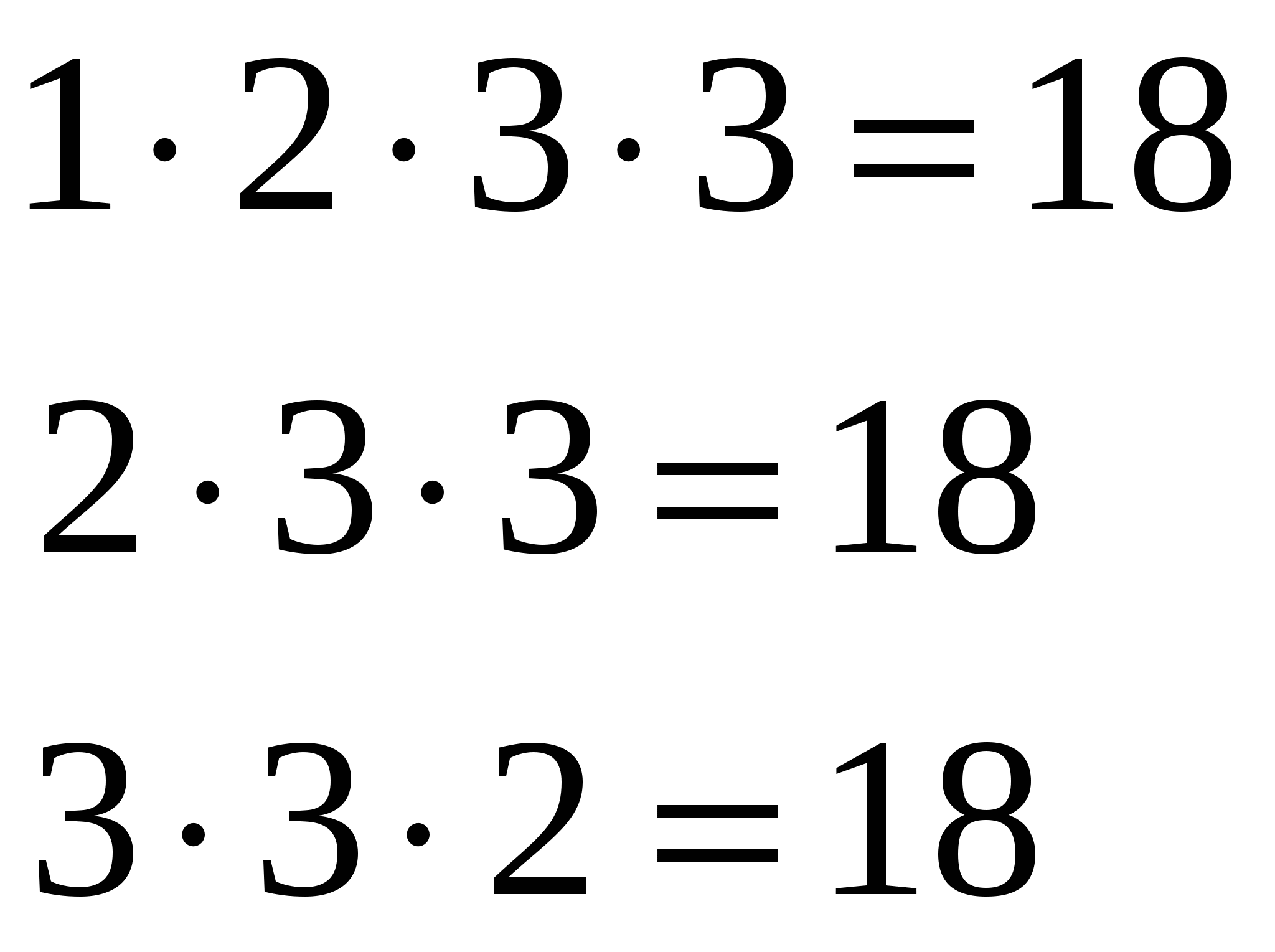

 5 5 75 5
5 5 75 5
 875 5 5625 5
875 5 5625 5
 0 2 24 2
0 2 24 2 представить в виде многочлена стандартного вида
представить в виде многочлена стандартного вида