Результаты изучения учебного предмета
Изучение математики в 7 классе дает возможность обучающимся достичь следующих результатов развития:
в личностном направлении:
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
креативность мышления, инициатива, находчивость, активность при решении математических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений;
в метапредметном направлении:
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (графики, диаграммы, таблицы, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера;
в предметном направлении:
овладение базовым понятийном аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура, уравнение, функция, вероятность) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;
умение работать с математическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;
развитие представлений о числе и числовых системах от натуральных до действительных чисел; овладение навыками устных, письменных, инструментальных вычислений;
овладение символьным языком алгебры, приемами выполнения тождественных преобразований рациональных выражений, решения уравнений, систем уравнений, неравенств и систем неравенств; умение использовать идею координат на плоскости для интерпретации уравнений, неравенств, систем; умение применять алгебраические преобразования, аппарат уравнений и неравенств для решения задач из различных разделов курса;
овладение системой функциональных понятий, функциональным языком и символикой; умение использовать функционально – графические представления для описания и анализа реальных зависимостей;
овладение основными способами представления и анализа статистических данных; наличие представлений о статистических закономерностях в реальном мире и о различных способах их изучения, о вероятностных моделях;
овладение геометрическим языком, умение использовать его для описания предметов окружающего мира; развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений;
усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне – о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;
умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объемов геометрических фигур;
умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях.
Используемые формы, способы и средства проверки и оценки результатов обучения.
Письменный контроль (самостоятельные и контрольные работы, проверка домашнего задания);
Тестовый (тестирование);
Устный опрос (собеседование, зачет)
Оценка письменных контрольных работ обучающихся по математике.
Ответ оценивается отметкой «5», если:
работа выполнена полностью;
в логических рассуждениях и обосновании решения нет пробелов и ошибок;
в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).
Отметка «4» ставится в следующих случаях:
работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);
допущены одна ошибка или есть два – три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).
Отметка «3» ставится, если:
допущено более одной ошибки или более двух – трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.
Отметка «2» ставится, если:
допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.
Оценка устных ответов обучающихся по математике
Ответ оценивается отметкой «5», если ученик:
полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;
изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;
правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;
показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;
продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;
отвечал самостоятельно, без наводящих вопросов учителя;
возможны одна – две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;
допущены один – два недочета при освещении основного содержания ответа, исправленные после замечания учителя;
допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.
Отметка «3» ставится в следующих случаях:
неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке учащихся» в настоящей программе по математике);
имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;
ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;
при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.
Отметка «2» ставится в следующих случаях:
не раскрыто основное содержание учебного материала;
обнаружено незнание учеником большей или наиболее важной части учебного материала;
допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.
Общая классификация ошибок
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
3.1. Грубыми считаются ошибки:
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
незнание наименований единиц измерения;
неумение выделить в ответе главное;
неумение применять знания, алгоритмы для решения задач;
неумение делать выводы и обобщения;
неумение читать и строить графики;
неумение пользоваться первоисточниками, учебником и справочниками;
потеря корня или сохранение постороннего корня;
отбрасывание без объяснений одного из них;
равнозначные им ошибки;
вычислительные ошибки, если они не являются опиской;
логические ошибки.
3.2. К негрубым ошибкам следует отнести:
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
неточность графика;
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
нерациональные методы работы со справочной и другой литературой;
неумение решать задачи, выполнять задания в общем виде.
3.3. Недочетами являются:
нерациональные приемы вычислений и преобразований;
- небрежное выполнение записей, чертежей, схем, графиков.
В рабочей программе предусмотрено 11 контрольных работ по темам:
Перечень контрольных работ
Входная контрольная работа.
Контрольная работа №1 «Выражения, тождества»
Контрольная работа №2 «Выражения, тождества, уравнения»
Контрольная работа №3 «Функции»
Контрольная работа №4 «Степень с натуральным показателем»
Контрольная работа №5 «Сумма и разность многочленов. Произведение многочленов»
Контрольная работа №6 «Многочлены»
Контрольная работа №7 «Разложение многочленов на множители»
Контрольная работа №8 «Формулы сокращенного умножения»
Контрольная работа №9 «Системы линейных уравнений»
Итоговая контрольная работа №10
Входная контрольная работа по алгебре – 7 класс
1 вариант
№ 1. Найти значение выражения:
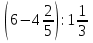 . .
№ 2. Решить уравнение:
2,4х – 0,5 = 2,2х – 6,5 .
№ 3. Постройте отрезок АВ, где А(-6;-1); В(3;2) и запишите координаты точек
пересечения этого отрезка с осями координат.
№ 4. Решите с помощью уравнения задачу:
В одной пачке лежало в 1,2 раза больше тетрадей, чем в другой. Сколько
тетрадей лежало в каждой пачке, если всего их было 198 ?
№ 5. В 7 классе 25% учеников посещают волейбольную секцию. Сколько всего
учеников в 7 классе, если секцию посещают 7 человек ?
Входная контрольная работа по алгебре – 7 класс
2 вариант
№ 1. Найти значение выражения:
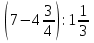 . .
№ 2. Решить уравнение:
3,6х – 0,8 = 4,4х – 3,8 .
№ 3. Постройте отрезок АВ, где А(-2;-3); В(1;6) и запишите координаты точек
пересечения этого отрезка с осями координат.
№ 4. Решите с помощью уравнения задачу:
В одном ящике лежало в 1,4 раза больше яблок, чем в другом. Сколько
яблок лежало в каждом ящике, если всего их было 168 ?
№ 5. В 7 классе 40% учеников посещают футбольную секцию. Сколько всего
учеников в 7 классе, если секцию посещают 12 человек ?
Входная контрольная работа по алгебре – 7 класс
3 вариант
№ 1. Найти значение выражения:
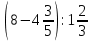 . .
№ 2. Решить уравнение:
2,5х – 0,2 = 2,2х – 6,5 .
№ 3. Постройте отрезок АВ, где А(3;2); В(-6;-1) и запишите координаты точек
пересечения этого отрезка с осями координат.
№ 4. Решите с помощью уравнения задачу:
В одной корзине лежало в 1,3 раза больше груш, чем в другой. Сколько
груш лежало в каждой корзине, если всего их было 69 ?
№ 5. В 7 классе 25% учеников посещают волейбольную секцию. Сколько всего
учеников в 7 классе, если секцию посещают 6 человек ?
Входная контрольная работа по алгебре – 7 класс
4 вариант
№ 1. Найти значение выражения:
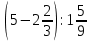 . .
№ 2. Решить уравнение:
1,4х – 0,3 = 1,2х – 3,7 .
№ 3. Постройте отрезок АВ, где А(2;4); В(-3;-2) и запишите координаты точек
пересечения этого отрезка с осями координат.
№ 4. Решите с помощью уравнения задачу:
В одном ящике лежало в 0,2 раза больше яблок, чем в другом. Сколько
яблок лежало в каждой ящике, если всего их было 144?
№ 5. В 7 классе 12 учеников, что составляет 10% от всех учащихся школы. Сколько всего
учеников в школе?
Контрольная работа №1 «Выражения, тождества»
Вариант 1.
• 1. Найдите значение выражения: 6x – 8y при x=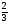 , y= , y=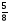 . .
• 2. Сравните значения выражений: -0,8x – 1 и 0,8x – 1 при x=6.
• 3. Упростите выражение:
а) 2x – 3y – 11x + 8y;
б) 5(2a + 1) – 3;
в) 14x – (x – 1) + (2x + 6).
4. Упростите выражение и найдите его значение:
-4(2,5a – 1,5) + 5,5a – 8 при a= -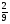 . .
5. Девочка в магазине купила 15 тетрадей по а рублей и 8 ручек по b рублей. Найдите стоимость покупки. Ответьте на вопрос задачи, если а = 20, b = 12.
6. Раскройте скобки: 3x – (5x – (3x – 1)).
Контрольная работа №1 «Выражения, тождества»
Вариант 2.
• 1. Найдите значение выражения: 16a + 2y при a=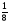 , y= , y= . .
• 2. Сравните значения выражений: 2 + 0,3a и 2 – 0,3a при a= -9.
• 3. Упростите выражение:
а) 5a + 7b – 2a – 8b;
б) 3(4x + 2) – 5;
в) 20b – (b – 3) + (3b – 10).
4. Упростите выражение и найдите его значение:
-6(0,5х – 1,5) - 4,5х – 8 при х =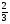 . .
5. В первой коробке лежало а карандашей, во второй на 10 карандашей больше, чем в первой, а в третьей в два раза больше, чем во второй. Найдите сколько всего было карандашей в трёх коробках. Ответьте на вопрос задачи, если а = 8.
6. Раскройте скобки: 2p – (3p – (2p – c)).
Контрольная работа №2 «Выражения, тождества, уравнения»
Вариант 1.
• 1. Решите уравнение:
а) 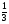 x = 12; в) 5x – 4,5 = 3x +2,5; x = 12; в) 5x – 4,5 = 3x +2,5;
б) 6x – 10,2 = 0; г) 2x – (6x – 5) = 45.
• 2. Таня в школу сначала едет на автобусе, а потом идёт пешком. Вся дорога у неё занимает 26 мин. Идёт она на 6 мин дольше, чем едет на автобусе. Сколько минут она едет на автобусе?
3. В двух сараях сложено сено, причём в первом сарае сена в 3 раза больше, чем во втором. После того как из первого сарая увезли 20 т сена, а во второй привезли 10 т, в обоих сараях сена стало поровну. Сколько всего тонн сена было в двух сараях первоначально?
4. Решите уравнение: 7x – (x + 3) = 3(2x – 1).
Контрольная работа №2 «Выражения, тождества, уравнения»
Вариант 2.
• 1. Решите уравнение:
а) 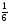 x = 18; в) 6x – 0,8 = 3x +2,2; x = 18; в) 6x – 0,8 = 3x +2,2;
б) 7x + 11,9 = 0; г) 5x – (7x + 7) = 9.
• 2. Часть пути в 600 км турист пролетел на самолёте, а часть проехал на автобусе. На самолёте он проделал путь, в 9 раз больший, чем на автобусе. Сколько километров турист проехал на автобусе?
3. На одном участке было в 5 раз больше саженцев смородины, чем на другом. После того как с первого участка увезли 50 саженцев, а на второй посадили ещё 90, на обоих участках саженцев стало поровну. Сколько всего саженцев было на двух участках первоначально?
4. Решите уравнение: 6x – (2x – 5) = 2(2x + 4).
Контрольная работа №3 «Функции»
Вариант 1.
• 1. Функция задана формулой у = 6x + 19. Определите:
а) значение у, если x=0,5; б) значение х, при котором у=1;
в) проходит ли график функции через точку А (-2;7).
• 2. а) Постройте график функции у=2х – 4.
б) Укажите с помощью графика, чему равно значение у при х=1,5.
• 3. В одной и той же системе координат постройте графики функций:
а) у = -2х; б) у = 3.
4. Найдите координаты точки пересечения графиков функций у = 47х – 37 и у = -13х + 23.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = 3х – 7 и проходит через начало координат.
Контрольная работа №3 «Функции»
Вариант 2.
• 1. Функция задана формулой у = 4х – 30. Определите:
а) значение у, если x= -2,5; б) значение х, при котором у = -6;
в) проходит ли график функции через точку В (7; -3).
• 2. а) Постройте график функции у = -3х + 3.
б) Укажите с помощью графика, при каком значении х значение у равно 6.
• 3. В одной и той же системе координат постройте графики функций:
а) у = 0,5х; б) у = -4.
4. Найдите координаты точки пересечения графиков функций у = -38х + 15 и у = -21х – 36.
5. Задайте формулой линейную функцию, график которой параллелен прямой у = -5х + 8 и проходит через начало координат.
Контрольная работа №4 «Степень с натуральным показателем»
Вариант 1.
• 1. Найдите значение выражения: 1 – 5х2 при х = -4.
• 2. выполните действия:
а) у7 ∙ у12; б) у20 : у5; в) (у2)8; г) (2у)4.
• 3. Упростите выражение:
а) -2ab3 ∙ 3a2 ∙ b4; б) (-2a5b2)3.
• 4. Постройте график функции у = х2. С помощью графика определите значение у при х = 1,5; х = -1,5.
5. Вычислите: 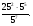
6. Упростите выражение:
а) 2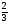 х2у8 ∙ (-1 х2у8 ∙ (-1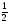 ху3)4; б) хn – 2 ∙ x3 – n ∙ x. ху3)4; б) хn – 2 ∙ x3 – n ∙ x.
Контрольная работа №4 «Степень с натуральным показателем»
Вариант 2.
• 1. Найдите значение выражения: -9p3 при p = -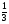 . .
• 2. Выполните действия:
а) с3 ∙ с22; б) с18 : с6; в) (с4)6; г) (3с)5.
• 3. Упростите выражение:
а) -4х5у2 ∙ 3ху4; б) (3х2у3)2.
• 4. Постройте график функции у = х2. С помощью графика функции определите, при каких значениях х значение у равно 4.
|
 Скачать 1.69 Mb.
Скачать 1.69 Mb. .
.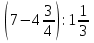 .
.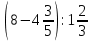 .
.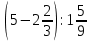 .
.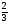 , y=
, y=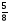 .
.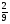 .
.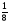 , y=
, y= .
.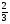 .
.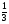 x = 12; в) 5x – 4,5 = 3x +2,5;
x = 12; в) 5x – 4,5 = 3x +2,5;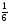 x = 18; в) 6x – 0,8 = 3x +2,2;
x = 18; в) 6x – 0,8 = 3x +2,2;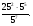
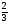 х2у8 ∙ (-1
х2у8 ∙ (-1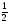 ху3)4; б) хn – 2 ∙ x3 – n ∙ x.
ху3)4; б) хn – 2 ∙ x3 – n ∙ x.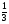 .
.