Калитвянская Нина Викторовна (фио) программа разработана на основе Авторская программа
 Скачать 1.69 Mb. Скачать 1.69 Mb.
|
5. Вычислите: 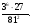 6. Упростите выражение: а) 3 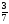 х5у6 ∙ (-2 х5у6 ∙ (-2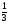 х5у)2; б) (аn + 1)2 : а2n. х5у)2; б) (аn + 1)2 : а2n.Контрольная работа №5 «Сумма и разность многочленов. Произведение многочленов» Вариант 1. • 1. Выполните действия: а) (3а – 4ах + 2) – (11а – 14ах); б) 3у2(у3 + 1). • 2. Вынесите общий множитель за скобки: а) 10аb – 15b2; б) 18а3 + 6а2. • 3. Решите уравнение: 9х – 6(х – 1) = 5(х + 2). • 4. Пассажирский поезд за 4 ч прошёл такое же расстояние, какое товарный за 6 ч. Найдите скорость пассажирского поезда, если известно, что скорость товарного на 20 км/ч меньше. 5. Решите уравнение: 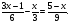 6. Упростите выражение: 2а(а + b – с) – 2b(а – b – с) + 2с(а – b + с). Контрольная работа №5 «Сумма и разность многочленов. Произведение многочленов» Вариант 2. • 1. Выполните действия: а) (2а2 – 3а + 1) – (7а2 – 5а); б) 3х(4х2 – х). • 2. Вынесите общий множитель за скобки: а) 2ху – 3ху2; б) 8b4 + 2b3. • 3. Решите уравнение: 7 – 4(3х – 1) = 5(1 – 2х). • 4. В трёх шестых классах 91 ученик. В 6 «А» на 2 ученика меньше, чем в 6 «Б», а в 6 «В» на 3 ученика больше, чем в 6 «Б». Сколько учащихся в каждом классе? 5. Решите уравнение: 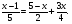 6. Упростите выражение: 3х(х + у + с) – 3у(х – у – с) – 3с(х + у – с). Контрольная работа №6 «Многочлены» Вариант 1. • 1. Выполните умножение: а) (с + 2)(с – 3); в) (5х – 2у)(4х – у); б) (2а – 1)(3а + 4); г) (а – 2)(а2 – 3а + 6). • 2. Разложите на множители: а) а(а + 3) – 2(а + 3); б) ах – ау + 5х – 5у. 3. Упростите выражение: -0,1х(2х2 + 6)(5 – 4х2). 4. Представьте многочлен в виде произведения: а) х2 – ху – 4х + 4у; б) ab – ac – bx + cx + c – b. 5. Из прямоугольного листа фанеры вырезали квадратную пластинку, для чего с одной стороны листа фанеры отрезали полосу шириной 2 см, а с другой, соседней, – 3 см. Найдите сторону получившегося квадрата, если известно, что его площадь на 51 см2 меньше площади прямоугольника. Контрольная работа №6 «Многочлены» Вариант 2. • 1. Выполните умножение: а) (а – 5)(а – 3); в) (3p + 2c)(2p + 4c); б) (5х + 4)(2х – 1); г) (b – 2)(b2 + 2b – 3). • 2. Разложите на множители: а) х(х – у) + а(х – у); б) 2а – 2b + са – сb. 3. Упростите выражение: 0,5х(4х2 – 1)(5х2 + 2). 4. Представьте многочлен в виде произведения: а)2а – ас – 2с + с2; б) bx + by – x – y – ax – ay. 5. Бассейн имеет прямоугольную форму. Одна из его сторон на 6 м больше другой. Он окружён дорожкой, ширина которой 0,5 м. Найдите стороны бассейна, если площадь окружающей его дорожки 15 м2. Контрольная работа №7 «Разложение многочленов на множители» Вариант 1. • 1. Преобразуйте в многочлен: а) (у – 4)2; в) (5с – 1)(5с + 1); б) (7х + а)2; г) (3а + 2b)(3a – 2b). • 2. Упростите выражение: (а – 9)2 – (81 + 2а). • 3. Разложите на множители: а) х2 – 49; б) 25х2 – 10ху + у2. 4. Решите уравнение: (2 – х)2 – х(х + 1,5) = 4. 5. Выполните действия: а) (у2 – 2а)(2а + у2); б) (3х2 + х)2; в) (2 + m)2 (2 – m)2. 6. Разложите на множители: а) 4х2у2 – 9а4; б) 25а2 – (а + 3)2; в) 27m3 + n3. Контрольная работа №7 «Разложение многочленов на множители» Вариант 2. • 1. Преобразуйте в многочлен: а) (3а + 4)2; в) (b + 3)(b – 3); б) (2x – b)2; г) (5y – 2x)(5y + 2x). • 2. Упростите выражение: (c + b)(c – b) – (5c2 – b2). • 3. Разложите на множители: а) 25y2 – a2; б) c2 + 4bc + 4b2. 4. Решите уравнение: 12 – (4 – x)2 = x(3 – x). 5. Выполните действия: а) (3x + y2)(3x – у2); б) (a3 – 6a)2; в) (a – x)2 (x + a)2. 6. Разложите на множители: а) 100а4 - 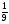 b2; б) 9x2 – (x – 1)2; в) x3 + y3. b2; б) 9x2 – (x – 1)2; в) x3 + y3.Контрольная работа №8 «Формулы сокращенного умножения» Вариант 1. • 1. Упростите выражение: а) (х – 3)(х – 7) – 2х(3х – 5); б) 4а(а – 2) – (а – 4)2; в) 2(m + 1)2 – 4m. • 2. Разложите на множители: а) х3 – 9х; б) -5а2 – 10аb – 5b2. 3. Упростите выражение: (у2 – 2у)2 – у2(у + 3)(у – 3) + 2у(2у2 + 5). 4. Разложите на множители: а) 16х4 – 81; б) х2 – х – у2 – у. 5. Докажите, что выражение х2 – 4х + 9 при любых значениях х принимает положительные значения. Контрольная работа №8 «Формулы сокращенного умножения» Вариант 2. • 1. Упростите выражение: а) 2х(х – 3) – 3х(х + 5); б) (а + 7)(а – 1) + (а – 3)2; в) 3(у + 5)2 – 3у2. • 2. Разложите на множители: а) с2 – 16с; б) 3а2 – 6аb + 3b2. 3. Упростите выражение: (3а – а2)2 – а2(а – 2)(а + 2) + 2а(7 + 3а2). 4. Разложите на множители: а) 81а4 – 1; б) у2 – х2 – 6х – 9. 5. Докажите, что выражение -а2 + 4а – 9 может принимать лишь отрицательные значения. Контрольная работа №9 «Системы линейных уравнений» Вариант 1. • 1. Решите систему уравнений: 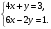 • 2. Банк продал предпринимателю г-ну Разину 8 облигаций по 2000 р. и 3000 р. Сколько облигаций каждого номинала купил г-н Разин, если за все облигации было заплачено 19 000 р.? 3. Решите систему уравнений: 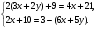 4. Прямая y = kx + b проходит через точки А (3;8) и В (-4;1). Напишите уравнение этой прямой. 5. Выясните, имеет ли решение система: 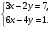 Контрольная работа №9 «Системы линейных уравнений» Вариант 2. • 1. Решите систему уравнений: 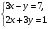 • 2. Велосипедист ехал 2 ч по лесной дороге и 1 ч по шоссе, всего он проехал 40 км. Скорость его по шоссе была на 4 км/ч больше, чем скорость на лесной дороге. С какой скоростью велосипедист ехал по шоссе, и с какой по лесной дороге? 3. Решите систему уравнений: 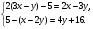 4. Прямая y = kx + b проходит через точки А (5;0) и В (-2;21). Напишите уравнение этой прямой. 5. Выясните, имеет ли решение система и сколько: 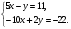 Итоговая контрольная работа №10 Вариант 1. • 1. Упростите выражение: а) 3а2b ∙ (-5а3b); б) (2х2у)3. • 2. Решите уравнение: 3х – 5(2х + 1) = 3(3 – 2х). • 3. Разложите на множители: а) 2ху – 6у2; б) а3 – 4а. • 4. Периметр треугольника АВС равен 50 см. Сторона АВ на 2 см больше стороны ВС, а сторона АС в2 раза больше стороны ВС. Найдите стороны треугольника. 5. Докажите, что верно равенство: (а + с) (а – с) – b(2а – b) – (a – b + c) (a – b – c) = 0. 6. На графике функции у = 5х – 8 найдите точку, абсцисса которой противоположна её ординате. Итоговая контрольная работа №10 Вариант 2. • 1. Упростите выражение: а) -2ху2 ∙ 3х3у5; б) (-4аb3)2. • 2. Решите уравнение: 4(1 – 5х) = 9 – 3(6х – 5). • 3. Разложите на множители: а) а2b – ab2; б) 9х – х3. • 4. Турист прошёл 50 км за 3 дня. Во второй день он прошёл на 10 км меньше, чем в первый день, и на 5 км больше, чем в третий. Сколько километров проходил турист каждый день? 5. Докажите, что при любых значениях переменных верно равенство: (х – у)(х + у) – (а – х + у)(а – х – у) – а(2х – а) = 0. 6. На графике функции у = 3х + 8 найдите точку, абсцисса которой равна её ординате. Приложение 1 Итоговый тест за курс 7 класса. Вариант 1. 1. Найдите значение выражения 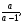 если а = 0,25. если а = 0,25.Ответ:______________. 2. Товар стоил 3200 р. Сколько стал стоить этот товар после снижения цены на 5%? А. 3040 р. Б. 304 р. В. 1600 р. Г. 3100 р. 3. Учащиеся класса в среднем выполнили по 7,5 заданий из предложенного теста. Максим выполнил 9 заданий. На сколько процентов его результат выше среднего? Ответ:______________. 4. Ряд состоит из натуральных чисел. Какая из следующих статистических характеристик не может выражаться дробным числом? А. Среднее арифметическое Б. Мода В. Медиана Г. Такой характеристики среди данных нет 5. Какое из уравнений не имеет корней? А. 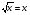 Б. Б. 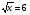 В. В. 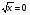 Г. Г.  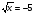 6. На координатной прямой отмечены числа А и В (рис. 1). Сравните числа -А и В. А 0 В Рис. 1 А. –А < В Б. –А > В В. –А = В Г. Сравнить невозможно. 7. Упростите выражение: а(а – 2) – (а – 1)(а + 1). Ответ:_________________. 8. Значения каких переменных надо знать, чтобы найти значение выражения (5а – 2b)(5a + 2b) – 4b(3a – b) + 6a(2b – 1)? А. а и b Б. а В. b Г. Значение выражения не зависит от значений переменных. 9. Решите уравнение: (х – 2)2 + 8х = (х – 1)(1 + х). Ответ:________________. 10. Решите систему уравнений: 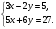 Ответ:________________. 11. За 3 ч езды на автомобиле и 4 ч езды на поезде туристы проехали 620 км, причём скорость поезда была на 10 км/ч больше скорости автомобиля? Обозначив через х км/ч скорость автомобиля и через у км/ч скорость поезда, составили системы уравнений. Какая из них составлена правильно? А. 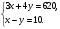 Б. Б. 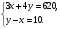 В. 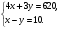 Г. Г. 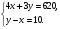 12. Какая из точек не принадлежит графику функции у = -0,6х + 1? А. (3; -0,8) Б. (-3; 0,8) В. (2; -0,2) Г. (-2; 2,2) 13. В какой координатной четверти нет ни одной точки графика функции у = -0,6х + 1,5? Ответ:________________. 14. Задайте формулой линейную функцию, график которой пересекает ось х в точке (2; 0) и ось у в точке (0; 7). Ответ:________________. Итоговый тест за курс 7 класса. Вариант 2. 1. Найдите значение выражения 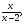 если х = 2,25. если х = 2,25.Ответ:______________. 2. Товар стоил 1600 р. Сколько стал стоить этот товар после повышения цены на 5%? А. 1760 р. Б. 1700 р. В. 1605 р. Г. 1680 р. 3. За смену токари цеха обработали в среднем по 12,5 деталей. Петров обработал за эту смену 15 деталей. На сколько процентов его результат выше среднего? Ответ:______________. 4. В ряду данных все числа целые. Какая из следующих характеристик не может выражаться дробным числом? А. Среднее арифметическое Б. Мода В. Медиана Г. Такой характеристики среди данных нет 5. Какое из уравнений не имеет корней? А. 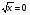 Б. Б. 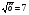 В. В. 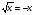 Г. Г.  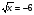 6. На координатной прямой отмечены числа В и С (рис. 2). Сравните числа В и -С. С 0 В Рис. 2 А. В > -С Б. В < -С В. В = -С Г. Сравнить невозможно. 7. Упростите выражение: х(х – 6) – (х – 2)(х + 2). Ответ:________________. 8. Значения каких переменных надо знать, чтобы найти значение выражения (3х – 4у)(3х + 4у) – 3х(3х – у) + 3у(1 – х)? А. х Б. у В. х и у Г. Значение выражения не зависит от значений переменных. 9. Решите уравнение: (х + 3)2 – х = (х – 2)(2 + х). Ответ:________________. 10. Решите систему уравнений: 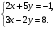 Ответ:________________. 11. Масса 5 см3 железа и 10 см3 меди равна 122 г. Масса 4 см3 железа больше массы 2 см3 меди на 14,6 г. Каковы плотность железа и плотность меди? Обозначив через х г/см3 плотность железа и через у г/см3 плотность меди, составили системы уравнений. Какая из них составлена правильно? А. 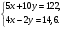 Б. Б. 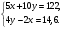 В. 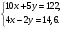 Г. Г. 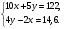 12. Какая из точек не принадлежит графику функции у = -1,2х – 1,4? А. (-1; -0,2) Б. (-2; -1) В. (0; -1,4) Г. (-3; 2,2) 13. В какой координатной четверти нет ни одной точки графика функции у = 1,8х – 7,2? Ответ:________________. 14. Задайте формулой линейную функцию, график которой пересекает ось х в точке (-4; 0) и ось у в точке (0; 3). Ответ:________________. СОГЛАСОВАНО Протокол заседания методического совета МБОУ Селивановская СОШ от______________ года №_1_ Председатель МС ______________/Пушкарёва Н.В./ (подпись) Ф.И.О. СОГЛАСОВАНО Заместитель директора по УР __________________/Пушкарёва Н.В./ (подпись) Ф.И.О. 20 года Дата Самостоятельная работа «Тождественные преобразования» Вариант 1
10х – 6у – 2х + 9 у
а) 3х + (9у – 2а); б) 12а – (-с + 5у – 4)
3 – 2(4у – 5) Самостоятельная работа «Тождественные преобразования» Вариант 2
13a – 5b + 4a – 7b
а) 3х + (11a – 6c); б) 2а – (-7x - 11у + 5)
4 – 2(3c + 7) Самостоятельная работа «Тождественные преобразования» Вариант 1
10х – 6у – 2х + 9 у
а) 3х + (9у – 2а); б) 12а – (-с + 5у – 4)
3 – 2(4у – 5) Самостоятельная работа «Тождественные преобразования» Вариант 2
13a – 5b + 4a – 7b
а) 3х + (11a – 6c); б) 2а – (-7x - 11у + 5)
4 – 2(3c + 7) Самостоятельная работа «Тождественные преобразования» Вариант 1
10х – 6у – 2х + 9 у
а) 3х + (9у – 2а); б) 12а – (-с + 5у – 4)
3 – 2(4у – 5) Самостоятельная работа «Тождественные преобразования» Вариант 2
13a – 5b + 4a – 7b
а) 3х + (11a – 6c); б) 2а – (-7x - 11у + 5)
4 – 2(3c + 7) |