Ульяновский государственный педагогический
 Скачать 1.43 Mb. Скачать 1.43 Mb.
|
Второй уровень самостоятельности можно назвать вариативной самостоятельностью. Самостоятельность на этом уровне про является в умении из нескольких имеющихся правил, определе ний, образцов рассуждении и т. п. выбрать одно определенное и использовать его в процессе самостоятельного решения новой задачи. На данном уровне самостоятельности учащийся показы вает умение производить мыслительные операции, такие, как сравнение, анализ. Анализируя условие задачи, ученик переби рает имеющиеся в его распоряжении средства для ее решения, сравнивает их и выбирает более действенное. Третий уровень самостоятельности — частично-поисковая са мостоятельность. Самостоятельность ученика на этом уровне проявляется в умении из имеющихся у него правил и предписаний для решения задач определенного раздела математики формиро вать (комбинировать) обобщенные способы для решения более широкого класса задач, в том числе и из других разделов мате матики; в умении осуществить перенос математических методов, рассмотренных в одном разделе, на решение задач из другого раздела или из смежных учебных предметов; в стремлении найти «собственное правило», прием, способ деятельности; в поисках нескольких способов решения задачи и в выборе наиболее рацио нального, изящного; в варьировании условия задачи и сравнении соответствующих способов решения и т. п. В названных прояв лениях самостоятельности присутствуют элементы творчества. Ученик на этом уровне обладает относительно большим набо ром приемов умственной деятельности — умеет проводить срав нение, анализ, синтез, абстрагирование и т. п. В его деятельности значительное место занимает контроль результатов и самоконт роль. Он может самостоятельно спланировать и организовать свою учебную деятельность. На внеурочных занятиях в III, а особенно в IV классе само стоятельность некоторых учащихся носит творческий характер, что находит выражение в самостоятельной постановке ими проб лемы или задачи, в составлении плана ее решения и отыскании способа решения; в постановке гипотез и их проверке; в проведе нии собственных исследований и т. п. Поэтому целесообразно выделить высший, четвертый уровень самостоятельности — твор ческую самостоятельность. В соответствии с выделенными уровнями осуществляются четыре этапа учебной работы. Каждый этап связан с предыдущим и с последующим и должен обеспечивать переход школьника с одного уровня самостоятельности на следующий. Первый этап ставит целью выход учащегося на первый уро вень самостоятельности. На этом этапе учитель знакомит уча щихся с элементарными формами познавательной деятельности, сообщая математические сведения, разъясняет, как можно было бы получить их самостоятельно. С этой целью он использует лекционную форму работы или рассказ, а затем организует са мостоятельную деятельность учеников, состоящую в изучении доступного материала учебного пособия и решении задач, пред варительно разработанных учителем в качестве примеров. Эта деятельность учителя и учащихся на занятиях соответствует аналогичной деятельности на уроках математики и довольно хорошо освещена в методической литературе. На данном этапе учитель организует элементарную работу учащихся по математическому самообучению: просмотр матема тических телевизионных передач во внеурочное время; самостоя тельное решение конкурсных задач из сборников, содержащих подробные решения или указания для контроля, причем с обяза тельным условием использования при решении некоторых из них знаний, полученных на внеурочных занятиях, участие во Всероссийском конкурсе «Кенгуру», «Эму». На втором этапе учебной работы преподаватель привлекает учащихся к обсуждению различных способов решения познава тельной задачи и отбору наиболее рационального из них; поощря ет самостоятельную деятельность учеников в сравнении способов. Учитель знакомит учащихся с общими и частными указаниями, содействующими самостоятельному выбору путей решения по знавательной задачи с помощью уже изученных приемов, спосо бов и методов решения аналогичных задач. На этом этапе педагог широко пользуется методом эвристической беседы, организует самостоятельное изучение учащимися нового материала по учеб ным пособиям, раскрывающим материал конкретно-индуктивным способом и содержащим большое число примеров различной трудности. На втором этапе продолжается работа по организации мате матического самообучения учащихся и руководству им. Ученики решают задачи из сборников конкурсных задач, готовятся к школьным математическим олимпиадам (обычно условия подго товительных задач помещаются на специальных стендах), чита ют доступную научно-популярную литературу, например, из серии «Занимательная математика». Руководство само обучением учащихся на этом этапе носит фронтально-индиви дуальный характер: учитель дает рекомендации по самообучению всем учащимся, но выполнение их не обязательно для всех; помощь преподавателя в организации математического самообу чения учащихся носит индивидуальный характер. Третий этап наиболее ответственный, так как именно на этом этапе должен произойти выход всех учащихся на основной уро вень самостоятельности. Здесь большое внимание уделяется организации самостоятельного изучения учащимися дополни тельной учебной, научно-популярной и научной математической литературы, сопровождаемого решением достаточного числа задач; подготовке рефератов и докладов по математике; творче скому обсуждению докладов и сообщений на семинарах, органи зуемых на факультативе (постановка и обсуждение гипотез, задач-проблем, математических методов, возможных обобщений и т. п.); участию в школьном конкурсе по решению задач, в школьной, районной или областной олимпиаде по математике, в заочных олимпиадах и конкур сах; самообучению учащихся с учетом индивидуальных интересов и потребностей. Например, в качестве рефератов могут быть предложены классические задачи древности: об учёных - математиках, о понятиях: точка, треугольник, действие умножение, сложение. На этом этапе учитель организует на занятиях обобщающие беседы по самостоятельно изученному школьниками материалу;
Большое внимание уде ляется индивидуальной работе с учащимися: оказание ненавяз чивой помощи некоторым ученикам в поисках путей решения задачи, в подготовке к математическим олимпиадам, в подборе литературы для рефератов и их письменном оформлении, в ор ганизации и осуществлении математического самообучения. Рассмотрим примеры. (Приложение 1) На четвертом этапе основной формой является индивидуаль ная работа с учащимися, дифференцируемая с учетом позна вательных интересов и потребностей и профессиональной ориен тации каждого. Самостоятельная работа школьника на этом этапе работы носит поисково-исследовательский характер и требует творческих усилий. Учащиеся самостоятельно в течение сравнительно длительного срока решают задачи, сформулирован ные ими самими или выбранные из предложенных учителем. Помощь преподавателя заключается в проведении индивидуаль ных консультаций, в рекомендации соответствующей литературы, в организации обсуждения найденного учеником доказатель ства и т. п. На этом этапе проводятся конкурсы по решению задач, само стоятельная подготовка победителей школьной математической олимпиады к районной (областной, республиканской) олимпиаде (под руководством учителя); продолжается работа по самообу чению. Наиболее глубоко и полно система учебной работы по разви тию самостоятельности и творческой активности школьников реализуется при изучении факультативных курсов по математике. Обучение через задачи Метод обучения математике через задачи базируется на сле дующих дидактических положениях: 1) Наилучший способ обучения учащихся, дающий им созна тельные и прочные знания и обеспечивающий одновременное их умственное развитие, заключается в том, что перед учащимися ставятся последовательно одна за другой посильные теорети ческие и практические задачи, решение которых дает им новые знания. 2) Обучение на немногочисленных, но хорошо подобранных задачах, решаемых школьниками в основном самостоятельно, способствует вовлечению их в творческую исследовательскую работу, последовательно проводя через этапы научного поиска, развивает логическое мышление. 3) С помощью задач, последовательно связанных друг с другом, можно ознакомить учеников даже с довольно сложными математическими теориями. 4) Усвоение материала курса через последовательное реше ние учебных задач происходит в едином процессе приобретения новых знаний и их немедленного применения, что способствует развитию познавательной самостоятельности и творческой ак тивности учащихся. Можно выделить следующие виды обучения через задачи на внеурочных занятиях.
Весь материал курса раскрывается через задачи в основном дедуктивным путем. Получен ные знания находят применение при решении творческих иссле довательских задач.
Рассмотрим более подробно каждый из этих видов обучения. Подготовительные задачи чаще всего располагаются в серии с нарастающей трудностью. Схематически ее можно изобразить так: А1—А2—А3—...—Ап, где Аk (k=1, 2, 3, .... n) — подготови тельная задача, решение которой способствует самостоятельному решению учеником задачи Ak+1. Каждая подготовительная задача должна быть небольшой по объему информации, доступной для самостоятельного реше ния учащимися. Особенно важно это для первых задач серии, так как успех в решении одной задачи стимулирует самостоятель ную деятельность школьника при решении следующей. Задачи подбираются средней трудности, чтобы быть доступными всем ученикам. Если взять слишком легкие задачи, то у сильных учащихся пропадает интерес к их решению. Слишком же трудные задачи исключают самостоятельность решения для всех учащих ся. При возникновении затруднений учителем должна быть оказана индивидуальная помощь. В ходе решения задач обязательно их письменное оформле ние, чтобы можно было, охватив решения всех задач серии, проследить пути к решению основной задачи-проблемы, сделать необходимые обобщения. Если первые задачи серии окажутся для какого-то ученика слишком легкими, он может по своему усмотрению начать письменное оформление решений с задачи Ak, т. е. с промежуточной задачи. Тогда для него подготовитель ная серия задач будет иметь вид Ak—Ak+1—...—An. Решения задач обсуждаются коллективно, анализируются различные способы решения, проводится обобщение полученных результатов, формулируется учебная проблема и намечается способ ее решения. Всячески поощряется самостоятельность суждений, отстаивание учащимися собственного мнения. (Приложение 1) Идея использования вспомогательных задач возникла на основе наблюдений психологов о том, что при решении сложной задачи учащиеся обычно ищут, под какой из уже известных типов задач можно было бы ее подвести. При этом они, анализируя условие задачи, осуществляя поисковые пробы, пытались вос пользоваться такими данными, которые способствовали бы пере носу уже имеющегося в их опыте (полученном при решении ранее встречающихся задач) общего или частного метода, способа или приема решения задач. То есть способы решения одной задачи оказывают существенное влияние на самостоятельные поиски решения другой. Вспомогательные задачи являются своеобразными указания ми к самостоятельной деятельности ученика при решении основ ной задачи. Они отличаются от указаний и готовых решений, имеющихся в большинстве пособий по математике для самостоя тельной подготовки к конкурсным экзаменам, тем, что не содер жат рецептов, не навязывают способ решения автора, не дают готового решения. Указание (подсказка) во вспомогательной задаче заключается в ее решении: нужно сначала самостоятельно решить вспомогательную задачу, а затем обнаружить содержа щуюся в ней подсказку. Обычно для ученика одной вспомога тельной задачи оказывается недостаточно. Тогда дается вторая вспомогательная задача и т. п. Образуется серия вспомогатель ных задач. Схематично основная задача А вместе с серией вспомога тельных задач A1, A2, ..., An изображается так: А: A1 —A2 — ... —An. Самостоятельная деятельность ученика начинается с решения задачи А. Если он за определенное время не сможет решить ее, то приступает к решению первой вспомогательной задачи А1: А—А1. В случае решения задачи А1 ученик снова возвраща ется к задаче А: А1—А. Если задача А снова не решается, то он обращается к задаче А2. Решив задачу A2, возвращается к зада че A и т. д. Возможен случай, когда школьник не сможет решить вспомогательную задачу А1. Тогда он приступает к решению задачи А2. Если и A2 не решается, то переходит к задаче A3 и так до An. От задачи An ученик последовательно возвращается к задаче А: An —An-1 — ... —A1—A. Возможна и другая последо вательность решения задач, что можно изобразить схемами: A —A1 — A—A2 —A — A3 —A или A —A1 — A—A2 —A1 — A—A3 —A2 —A1—A и т. д. Составление вспомогательных задач наталкивается на серьез ные трудности. Для решения задачи Л может соответствовать и другая серия вспомогательных задач, отличная от указанной, например В1, В2, ..., Bk Трудность заключается в отборе лучшей (оптимальной) серии для конкретного ученика. Далее, серия может быть и нелинейна. Это получается тогда, когда для реше ния задачи A нужно знать способы решения сразу двух (или нескольких) задач. Схематическое изображение этой ситуации таково: A: 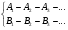 Трудность заключается в том, что одна и та же серия вспомо гательных задач для разных учащихся имеет различную эффек тивность: для одних серия слишком длинна (содержит много задач), для других коротка, одни и те же задачи для одних слишком легки, для других трудны и т. п. Кроме того, вспомо гательные задачи навязывают ученику определенный путь реше ния. Но и при подсказке учителя также навязывается ученику способ решения, намеченный учителем. Опыт применения вспомогательных задач на кружковых и факультативных занятиях по математике показывает, что школь ники, научившись самостоятельно решать задачи с помощью вспомогательных задач, предложенных учителем, замечают, что среди задач A1 —A2 — ... —An имеются и такие, которые либо уже были решены ими ранее, либо решаются способами (приемами), известными им. Это наталкивает учащихся на мысль, что при решении новой задачи следует самостоятельно отыскивать среди уже решенных ранее задач родственные данной и использовать их в качестве вспомогательных. Так воспитывается умение при самостоятельном решении задач возвращаться к своему опыту и применять его при продвижении вперед. Последнее является важным звеном умения решать задачи, умения самостоятельно приобретать новые знания. Курсы, построенные на задачах, не содержат деления мате риала на теоретическую и практическую части. Сами задачи — это и есть изучаемый курс. Поэтому и содержание задач, и спо собы решения их направлены как на вооружение учащихся теоретическими знаниями, так и на выработку умений и закреп ление навыков. Рассматриваемые определения обычно вклю чаются в содержание задач. Возможна формулировка опреде лений и отдельно от задач. Любая тема состоит из серии задач, которые должны быть полностью решены каждым учеником, так как только в этом случае достигается полное усвоение определенной математи ческой теории. Однако в индивидуальные задания могут быть включены задачи подготовительные, вспомогательные или задачи для самоконтроля, которые не обязательны для всех учеников. Перед изучением темы организуется пропедевтическая работа, ставящая своей целью подготовить учеников к самостоятель ному активному изучению материала. В частности, здесь выявля ются и ликвидируются пробелы в знаниях и формируются необхо димые предварительные представления. Затем учитель в форме лекции или беседы вводит учеников в тему, намечает круг вопро сов, подлежащих изучению, формулирует сам или подводит учащихся к самостоятельной формулировке первой проблемной задачи. Основным этапом занятий является самостоятельное решение школьниками задач. Учащимся в процессе самостоятельной ра боты разрешается пользоваться справочниками и своими предыдущими работами, поскольку необходимо умственное развитие, умение самостоя тельно решить возникающие задачи. Индивидуальная помощь учителя носит характер не подсказки, а направления на верный путь решения, для чего используются вспомогательные задачи. Расположение задач в серии по принципу нарастающей труд ности стимулирует развитие самостоятельности учеников. Обу чение с использованием серии вспомогательных задач строится по принципу от сложного к простому, от трудного к более лег кому, что способствует формированию элементов творчества, стимулирует поиски учащимися способов решения, побуждает их мыслить. После решения всех задач серии проводится коллек тивное обсуждение результатов. Полученный материал обобща ется для последующего применения полученных знаний при ре шении нового класса задач, делаются теоретические выводы. Всячески поощряется самостоятельность учеников в суждениях, в отстаивании собственного мнения. Как показал опыт, обучение через задачи на внеурочных занятиях обеспечивает развитие самостоятельности и творческой активности учащихся, способствует приобретению прочных и осознанных знаний, развивает умение сравнивать, обобщать, делать творческие выводы из решенных задач, поддерживает интерес к математике. Активизация внеклассной работы Внеклассная работа по математике в ее традиционном толко вании проводится в школе учителем во внеурочное время с учащимися, проявляющими к математике интерес. Эта работа планируется учителем и по мере необходимости корректируется. Государственных программ по внеклассной работе нет, как нет и норм оценок. На внеклассные мероприятия и занятия ученики приходят по желанию, без всякой предварительной записи. Если у ученика пропадет интерес к внеклассной работе, он прекращает свое участие в ней. Активизация внеклассной работы по матема тике призвана не только возбуждать и поддерживать у учеников интерес к математике, но и желание заниматься ею дополнительно как под руководством учителя во внеурочное время, так и при целенаправленной самостоятельной познавательной деятель ности по приобретению новых знаний, т. е. путем самообучения. Одной из форм внеурочной работы являются конкурсы, кото рые обладают большим эмоциональным воздействием на участ ников и зрителей. (Приложение 1) Организация самообучения школьников с учётом индивидуальных интересов и потребностей В дидактике установлено, что самостоятельная деятельность учащихся по приобретению новых знаний по собственной ини циативе, сверх программы школьного предмета, возможна лишь при наличии серьезного интереса к предмету, увлечения рас сматриваемыми проблемами, переходящего в познавательную потребность приобретать сверхпрограммные знания в соответ ствии с индивидуальными интересами и потребностями. С помощью анкет, в ходе личных бесед можно установить, почему тот или иной ученик посещает занятия кружка или факультатива. В младшем возрасте, как правило, это интерес к математике как любимому учебному предмету. Для учителя полученные данные нужны для эффективного при менения индивидуального подхода к школьникам во внеурочной работе, корректировки своей работы, направленной на развитие интереса учащихся в ходе внеурочных занятий. В противном случае первоначальный интерес к математике, не получая под крепления и развития, гаснет и ученики прекращают посещать внеурочные мероприятия. Более того, они перестают самостоя тельно заниматься математикой дома, фактически прекращают самообучение. Интерес к математике формируется с помощью не только математических игр и занимательных задач, рассмотрения со физмов, разгадывания головоломок и т. п., хотя и они необхо димы, но и логической занимательностью самого математического материала: проблемным изложением, постановкой гипотез, рас смотрением различных путей решения проблемной ситуации, ре шением задач или приемами формирования познавательного интереса к математике. Разбор предложенных способов проходил на расширенном заседании математического кружка с привлечением учащихся из группы факультатива и приглашением желающих и вызвал неподдельный интерес у присутствующих. Необходимые вычисле ния проводились с помощью микрокалькулятора. Самообучение школьника невозможно без его умения и жела ния работать с математической книгой. Подбору математической литературы для самообучения учи телю приходится уделять большое внимание. Установлено, что учащиеся по-разному работают над книгой: одни стараются побыстрее пройти теоретический материал и приступить к реше нию задач, другие больше внимания уделяют, наоборот, теорети ческим вопросам. Первым не нравятся многословные учебники и пособия, они предпочитают краткие дедуктивные доказатель ства; вторые предпочитают книги с подробными выкладками, пояснениями, индуктивными выводами, примерами и т. п. С учетом избирательного отношения учеников к математичес ким книгам можно рекомендовать для самообучения не одно учебное пособие, а несколько, чтобы ученики сами выбирали то, которое им больше подходит по их индивидуальным склонностям и способностям. Правда, учителю в этом случае труднее конт ролировать их самостоятельную работу над книгой и проводить консультации. Зато самообучение школьников будет более эф фективным. Большое значение для стимулирования самообучения имеет организация обзоров изученной учащимися математической ли тературы, ее обсуждение на читательских конференциях или в устных журналах. Обычно делается это так. Объявляется тема для обзора и рекомендуется литература. Список литературы помещается на стенде. Там же указывается расписание консуль таций. Дается время для подготовки, назначается место и время проведения. Обзор литературы делают два-три ученика, они же отвечают на вопросы. Впрочем, отвечать могут и присутствующие ученики и учитель, а также дополнять или поправлять докладчиков. При этом возникают споры, выдвигаются гипотезы, находятся новые решения и т. д. Для самостоятельного обучения очень важно воспитать у уча щихся потребность в самостоятельном поиске знаний и их прило жении. Поэтому одной из задач является приобщение учеников к решению задач по своей инициативе, сверх школьной програм мы. Одним из средств является математическая олимпиада. Школьники убеждаются на собственном опыте, что, чем больше разнообразных задач они самостоятельно решают, тем значитель нее их успехи не только в школьной, но и в районной олимпиаде. Это служит дополнительным стимулом к самообучению. Одним из условий самообучения является умение ученика планировать свою самостоятельную внеурочную познавательную деятельность по приобретению знаний. Учитель помогает ему в составлении индивидуальных планов самообучения и в их реали зации. Самообучение школьника про водится обычно по плану, подсказанному учителем, а в некоторых случаях он прибегает к совету учителя или руководствуется его рекомендациями. Выяснив планы учащихся, учитель осуществлял индивидуаль но-групповое педагогическое руководство самообучением школь ников, которое проводилось в следующих направлениях: — корректирование (уточнение, детализация) индивидуаль ных планов самообучения; — подбор учебной, научно-популярной и научной литературы по математике для самостоятельного изучения; — более конкретное ознакомление каждого учащегося с пред полагаемой дальнейшей деятельностью и уточнение места и зна чения математических знаний в этой деятельности; — проведение индивидуальных и групповых консультаций по вопросам самообучения; Чтобы педагогическое руководство самообучением школьников было эффективным, целесообразно осуществлять определенную дифференциацию, которая по сути будет индивидуально-груп повой. Это обусловлено тем, что учащихся по их познаватель ным интересам и практическим потребностям, которые они хотят удовлетворить, занимаясь самообразованием, можно разделить на условные группы. К первой группе можно отнести учащихся с ярко выраженной интеллектуальной потребностью в углубленном изучении матема тики. Вторую группу составляют школьники, познавательные ин тересы которых у них обусловлены не потребностями в дальнейшей дея тельности, а исключительно направлениями выбранными родителями. И наконец, в отдельную четвертую группу целесообразно объединить учащихся, познавательные интересы которых часто являются раз личными случайными мотивами. Включение учеников в ту или иную группу учитель осуществ ляет по результатам индивидуальных бесед с учащимися и их родителями, а также с помощью анкетирования. Контроль за самообучением школьников можно осуществлять различными способами. Наиболее эффективный — через конкурсы по решению задач и различные математические состязания, в том числе и межпредметного содержания. Конкурс желательно проводить в несколько заочных туров и заключительный очный. Решения задач участники конкурсов могут давать любые, но за каждый способ решения одной и той же задачи очки начисляются отдельно. Это поощряет поиски новых оригинальных путей ре шения задачи, использование теоретического материала из различных рекомендованных учителем по определенной теме математических книг. Условия задач помещаются на стенде. Там же указываются конкурсные требования, сроки сдачи письменных работ, место и время обсуждения представленных решений. Об эффективности математического самообучения учитель может составить себе представление по многим критериям. При ведем некоторые из них: а) повышение количества учащихся, изучающих дополнительную литературу; б) смещение стержневого познавательного интереса школьников в сторону математики; в) массовое применение в самостоятельных, контрольных и зачетных работах, при решении конкурсных и олимпиадных задач математических знаний, полученных в результате само обучения; г) широкое участие в различных формах математи ческого образования в системе внешкольного обучения: в заочной математической олимпиаде «Кенгуру», в районных, областных олимпиадах, Такая информация поможет учителю своевременно вносить коррективы в свою работу по организации самообучения учеников, способствовать повышению самостоятельности и творческой активности школьников для получения сверхпрограммных мате матических знаний в соответствии с их индивидуальными инте ресами, потребностями, планами дальнейшей деятельности. Домашняя работа одна из видов организации самостоятельной деятельности младших школьников Домашняя учебная работа – это форма организации самостоятельного, индивидуального изучения школьниками учебного материала во внеучебное время. Значение домашней учебной работы, особенно в начальных классах, состоит в следующем. Выполнение домашних заданий помогает глубже понять учебный материал, способствует закреплению знаний, умений и навыков благодаря тому, что учащийся самостоятельно воспроизводит изученный на уроке материал и ему становится более ясно, что он знает, а чего не понимает. Н.К.Крупская в статье ''Методика задавания уроков на дом'' писала: ''Уроки на дом имеют большое значение. Правильно организованные они приучают к самостоятельной работе, воспитывают чувство ответственности, помогают овладевать знаниями, навыками’’ (6). Домашние задания для младших школьников – это шаг к самостоятельному добыванию знаний. Их выполнение способствует воспитанию самостоятельности, ответственности и добросовестности ученика в процессе обучения. Домашняя работа активизирует мыслительную деятельность ученика, т.к. ему приходится самому искать пути, средства и приёмы рассуждений и доказательств. Они приучают к самоконтролю, ведь рядом нет ни учителя, ни товарищей, которые могли бы помочь разъяснениями, способствуют формированию умений и навыков организационного труда: учащиеся должны самостоятельно организовать своё рабочее место, соблюдать установленный режим времени, подготавливать необходимое оборудование и учебные материалы. Основные требования к организации домашних заданий следующие.
Не следует также давать задания перед выходными и праздничными днями. Дети в эти дни отдыхают вместе с родителями и могут совершать туристские прогулки, посещать музеи, парки. Полезно один день в неделю дать отдых от напряжённой учебной работы.
Для более трудных заданий нужно предусмотреть резерв времени. Например, если в классе ученики выполняют задание за 10 минут, то на самостоятельное выполнение подобного задания дома нужно выделять примерно 15 минут.
Одним из активных средств заинтересованности детей является связь домашней работы с жизненным опытом ребёнка: наблюдения за явлениями, событиями окружающей действительности; составление текстов, математических задач, примеров на основе наблюдений за реальными явлениями, близкими детям; проведение возможных измерений и отдельных практических работ.
В начальных классах учитель систематически собирает тетради и проверяет выполнение домашних и классных работ.
При выполнении домашнего задания способ самостоятельности мыслительной деятельности ученика в основном повторяет существенные черты способа рассуждения учителя или логики изложения материала в учебном пособии. Однако в отсутствие учителя логика мышления ученика более самостоятельна. Он не может обратиться к учителю с вопросами и сомнениями, не может также ждать со стороны пояснений, наводящих вопросов, советов, одобрений или замечаний. Это придаёт своеобразную индивидуальную структуру мыслительной деятельности при выполнении домашних заданий. Для учителя большое значение имеет проникновение в мир самостоятельного мышления ребёнка, чтобы своевременно исправить недостатки и развить преимущества самостоятельного заучивания материала. На процесс выполнения домашнего задания влияет не только глубокая, понятная и интересная система объяснения учителем материала, но и весь облик учителя, его нравственные качества, отношение к детям, порядок и система его работы. Ученик не только выучивает домашнее задание, но и приспосабливается к запросам и требованиям учителя. Учителю важно видеть то общее, что характерно для ученика в классе и дома, и те особенности, которые возникают в мышлении и мотивации ребёнка при выполнении домашних заданий. Домашнее задание – необходимая часть процесса усвоения математического содержания в младшем школьном возрасте Существует, по меньшей мере, два обоснования необходимости домашнего задания, вытекающие из его педагогической функции. Первое следует из того факта, что одной из важнейших задач нашего образования является приобретение всеми учащимися (равных) основополагающих знаний и умений, но, однако, существуют различия в скорости восприятия и, следовательно, во времени, требующемся для усвоения материала отдельными учениками. Для школьников с высокой степенью обучаемости оказывается достаточным минимальное число упражнений, чтобы научиться решать те или иные задачи, примеры, уравнения. Школьникам, усваивающим материал медленнее, необходимо больше упражнений и времени. Конечно, нужно стремиться к тому, чтобы на самом уроке уделять больше времени тренировке, учитывая при этом индивидуальные особенности учащихся. Тем не менее, нельзя думать, что только на уроке каждый ученик может овладеть прочными знаниями и умениями. Здесь необходимы домашние задания. Но следует помнить, что нужна строгая дифференциация, так как нелепо было бы заставлять быстро усваивающих материал школьников выполнять дома упражнения, с какими они легко уже справились на уроке. Второе следует из того значения, которое имеет домашнее задание для развития определённых личностных качеств. Развитие определённых качеств личности зависит от того, насколько они проявляются в деятельности. Личностные качества, не пробуждаемые в деятельности, т.е. оказавшиеся не востребованными, остаются неразвитыми. С этой точки зрения стоит подойти к проблеме воспитания самостоятельности и ответственности. На уроке учитель, направляя действия школьников, стремится повышать степень самостоятельности учеников. Эта степень выше в том случае, когда учитель только ставит задание, а ученики затем длительное время работают сами. Задания такого рода требуют достаточно высокой интеллектуальной самостоятельности. Однако если подобные ситуации единичны и не составляют системы, то для реальной жизни этого оказывается недостаточно. Иногда одарённый ученик терпит поражение в жизни, так как ему не хватает силы воли, самодисциплины, чувства долга и ответственности или других черт характера, необходимых для самостоятельной деятельности не менее чем интеллектуальные предпосылки. Но на уроке развитие этих качеств может быть лишь только намечено, а не реализовано полно, так как для этого необходимы постоянные осознанные действия ученика. А у него нередко нет выбора, когда, в какой последовательности, за какое время и какими средствами выполнять задание. Всё это за него решено учителем и планом урока – должно быть решено, чтобы образовательные потенции урока не снижались. Здесь кроется одна из основных причин того, почему даже самый лучший урок не позволяет отказаться от домашнего задания. Итак, нет необходимости задавать на дом то, что достигнуто на уроке; тем не менее, домашнее задание – неизбежная составная часть и необходимое дополнение к хорошему уроку, потому что лишь при единстве урочной и внеурочной работы учащихся могут быть достигнуты образовательные и воспитательные цели. Дифференцированные домашние задания по математике в работе с двумя, тремя классами в начальной школе Развитие индивидуальности каждого школьника – требование, в реализации которого домашнему заданию отводится особая роль. Поскольку дифференцированные домашние задания до сих пор встречаются в наших школах скорее как исключение, мы хотели бы ещё раз вернуться к этой проблеме. Говоря об оптимальном развитии каждого школьника, мы имеем в виду необходимость:
На уроке, который для всех школьников протекает практически одинаково, создаются основные предпосылки для развития индивидуальности. Следует ли из этого, что домашние задания обязательно должны быть для всех учащихся одинаковыми? Во многих случаях: да. Если домашнее задание используется при предъявлении нового материала, для применения полученных знаний, т.е. во всех случаях, когда требуется участие каждого школьника, имеет смысл единое домашнее задание. В другой ситуации уместным будет дифференцированное домашнее задание. Мы уже выяснили: для школьников, которые овладели навыками выполнения определённых заданий, повторное выполнение таких же заданий - требование заниженное. Было бы лучше освободить этих ребят от обязательного домашнего задания и посоветовать им поработать над заданием повышенной сложности. Именно домашнее задание позволяет успешней использовать индивидуальные особенности и учитывать склонности учащихся. Принимать во внимание особенности работы с двумя классами, особые интересы слабоуспевающих и малоактивных учащихся, использовать эти интересы, развивать связанные с ними знания и способности с помощью целенаправленных домашних заданий – вот что необходимо для того, чтобы разорвать заколдованный круг: '' слабый ответ – негативная оценка – неудача – дезинтерес ''. Индивидуальная работа с учащимися при выборе домашнего задания предусматривает дифференцированный подход, обращение к конкретному школьнику, знание его особенностей, слабых и, в первую очередь, сильных сторон. В этом суть: не заострять внимание на возможных многочисленных больших и маленьких недостатках, поскольку они и так подчёркиваются слишком часто. Дифференцированные домашние задания удовлетворяют потребность учащихся в тренировке, позволяют восполнить пробелы в знаниях. Индивидуальные домашние задания должны получать и хорошо успевающие и одарённые школьники, потому что такие задания способствуют развитию их способностей, углублению их знаний. Особые задания должны ставить перед учащимися трудности, преодоление которых сделает более плодотворной работу на уроке. Индивидуальные домашние задания позволяют испытывать чувство успеха и тем школьникам, которые успевают на ''плохо'' и ''удовлетворительно''. Такое задание даёт этим школьникам возможность проявить себя, свои сильные стороны, тем самым, делая более позитивным отношение ребят к обучению в школе. Индивидуальные задания не должны даваться от случая к случаю. Продуманная их система даст возможность неуверенным ученикам укрепиться в своих возможностях, сильным развить свои интересы до глубокой увлечённости, и тех и других научит самостоятельному познанию. Домашние задания по математике, которые может давать учитель учащимся, весьма разнообразны. Их содержание определяется характером изучаемого материала, учебными целями, которые решаются на уроках, уровнем сформированности самостоятельной учебной деятельности. По своим частным целям домашние задания можно разделить на следующие виды: а) домашние задания для подготовки учащихся к очередной теме; б) задания для повторения и закрепления теоретических знаний; в) задания для обобщения изученного учебного материала; г) задания для выработки прочных умений и навыков в решении задач (задания по решению готовых задач из учебника, составление задач, подбор задач на определённую тему). По своему характеру домашние задания могут быть: а) теоретические (изучение, повторение или обобщение теоретического учебного материала); б) практические (изготовление пособий); в) решение конкретно-практических задач. По срокам выполнения домашние задания делятся на такие виды: а) одноурочные задания, которые необходимо выполнять к следующему уроку; б) длительные задания, выполнение которых рассчитано на срок от недели и более; в) задания с неопределённым сроком выполнения. По охвату учащихся домашние задания можно разделить на такие виды: а) задания для всех учащихся класса; б) индивидуальные задания; в) групповые задания, которые даются для коллективного выполнения группой учащихся. По характеру требований задания делятся на: а) обязательные, выполнение которых обязательно для всех учащихся класса или для отдельных учащихся, если это групповые или индивидуальные задания; б) желательные или свободные задания, которые даются учащимся в форме пожелания их выполнить. Они могут быть даны, например, в такой форме: ''Из задач (называют номера задач по учебнику) решите столько, сколько считаете нужным, и какие хотите''. Важнейшей целью домашних заданий является развитие у учащихся потребности в домашних занятиях по собственной инициативе. Такие занятия учащихся являются весьма надёжным показателем сформированности самостоятельной учебной деятельности. Конечно, формирование такой потребности есть длительный, многолетний процесс. В младших классах большинство учащихся нуждаются в чётких и определённых домашних заданиях, в объяснении и показе способа их выполнения. Очень важно научить учащихся уже с 1 класса правильно, разумно выполнять домашние задания, разумно готовиться к очередному уроку. Но постепенно надо приучать учащихся к самостоятельной постановке целей для домашних занятий, самостоятельному выбору содержания этих занятий. Каждое проявление инициативы ученика в этом направлении нужно всячески поощрять независимо от характера результатов этих занятий, нужно создавать вокруг такой инициативы положительное общественное мнение в классе. Развитию самостоятельных домашних занятий учащихся способствуют задания, требующие достаточно длительной творческой работы: написание докладов на математические темы; построение алгоритма решения задач какого-либо вида и т.д. По мере формирования у учащихся потребности и привычки к самостоятельной домашней работе нужно уменьшить число обязательных домашних заданий, давать их реже, но более содержательные и сложные по характеру. В конечном итоге необходимо выработать у учащихся стойкую привычку к подготовке к каждому очередному уроку по собственной инициативе. Итак, при подготовке домашнего задания необходимо выяснить, требует ли оно участия всех учащихся. Если нет – уместно дифференцированное задание. Использование дифференцированных домашних заданий возможно для закрепления материала, для развития индивидуальных способностей учащихся и их применения в интересах всего классного коллектива. Использование индивидуальных заданий возможно в воспитательных целях, а также для развития способностей особо одарённых детей. Система заданий Система заданий должна содержать достаточное число примеров и упражнений, обеспечивающих формирование вычислительных умений и навыков, а также позволяющих строить обобщения и выводы относительно расширения понятий о числе. Система заданий для домашней работы должна обеспечивать усвоение всех базовых математических знаний, умений и навыков в органическом единстве с общеучебными. А значит, она должна удовлетворять определённым требованиям. Под дидактическими требованиями мы понимаем положения, определяющие состав, структуру, содержание системы заданий, а также приёмы их включения в процесс обучения математике, ориентированный на формирование полноценной УД младших школьников. Исходя из этого, разработаны следующие требования к системе заданий для домашней работы:
Реализация этих требований зависит от уровня сформированности приёмов учебной деятельности школьников, овладения ими приёмами реализации самостоятельной работы. |