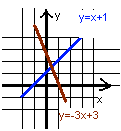Учебнику Мордкович А. Г. Алгебра, 7 по теме «Система двух линейных уравнений с двумя переменными» Сапко Екатерина Николаевна учитель математики Одинцово 2013
 Скачать 0.49 Mb. Скачать 0.49 Mb.
|
| Тема: Метод подстановки, п.12; 2. Обобщенная цель урока: формирование познавательных учебных действий и способностей учащихся решать системы линейных уравнений с двумя переменными методом подстановки; Ц 1. приобретение учебной компетентности по теме; Ц 2. контроль усвоения знаний; Ц 4. применение знаний и навыков по теме; 3. Задачи: предметные: ввести понятия метода подстановки; метапредметные: развивать умение решать рационально системы уравнений методом подстановки ; личностные: формировать интерес к математике; 4. Тип урока: урок построения системы знаний 5. Формы работы учащихся: исследовательская учебно-познавательная 6. Необходимое техническое оборудование: персональный компьютер, проектор, экран. 7. Структура и ход урока представлены в таблице 9. На каждом этапе урока учитель и учащиеся выполняют конкретные действия (табл. 9), связанные с задачами этапов и познавательными УУД. 8. Перечень используемых ЦОР и ЭОР на данном уроке (таблица 10). Таблица 9. Структура и ход урока «Системы линейных уравнений как математическая модель реальных ситуаций»
Таблица 10. Перечень используемых ЦОР и ЭОР на данном уроке
Таблица 11. Методы решения систем линейных уравнений с двумя переменными
3.2. Фрагменты уроков по избранным вопросам в соответствии с темой «Системы двух линейных уравнений с двумя переменными» При этой деятельности используются познавательно-логические УУД: сравнение, конкретизация, анализ, обобщение; общеучебные познавательные УУД: структурирование информации, составления схемы определения понятия. При этой деятельности формируются регулятивные УУД: прием коррекции собственной УПД; коммуникативные УУД. При этой деятельности используются регулятивные УУД. Фрагмент урока № 1. Системы двух линейных уравнений с двумя переменными как математические модели реальных ситуаций, п. 14.
Устный счет. 1) Выразить х через у: х - 5у = 7. 2) Выразить у через х: 6х – у = 5; 4х + 2у = 18. 3) Решением системы уравнений  х + у = 39, является пара (25; 14), (24; 15), (18; 7). х + у = 39, является пара (25; 14), (24; 15), (18; 7).х – у = 11; 4) Сложите два уравнения х + 15у = 27 и 3х-12у = 43. 5) Вычтите из уравнения 3х + у =13 уравнение -2х + 2у = 2. 6) Сколько решений имеет система, если графики уравнений системы пересекаются?
Постановка цели и формулирование темы урока.
Подготовка мышления детей: актуализация ЗУН, достаточных для используемых на уроке способов действий; тренировка соответствующих мыслительных операций. Изучение нового материала. Работа с ЦОР: Составление системы уравнений, №180572 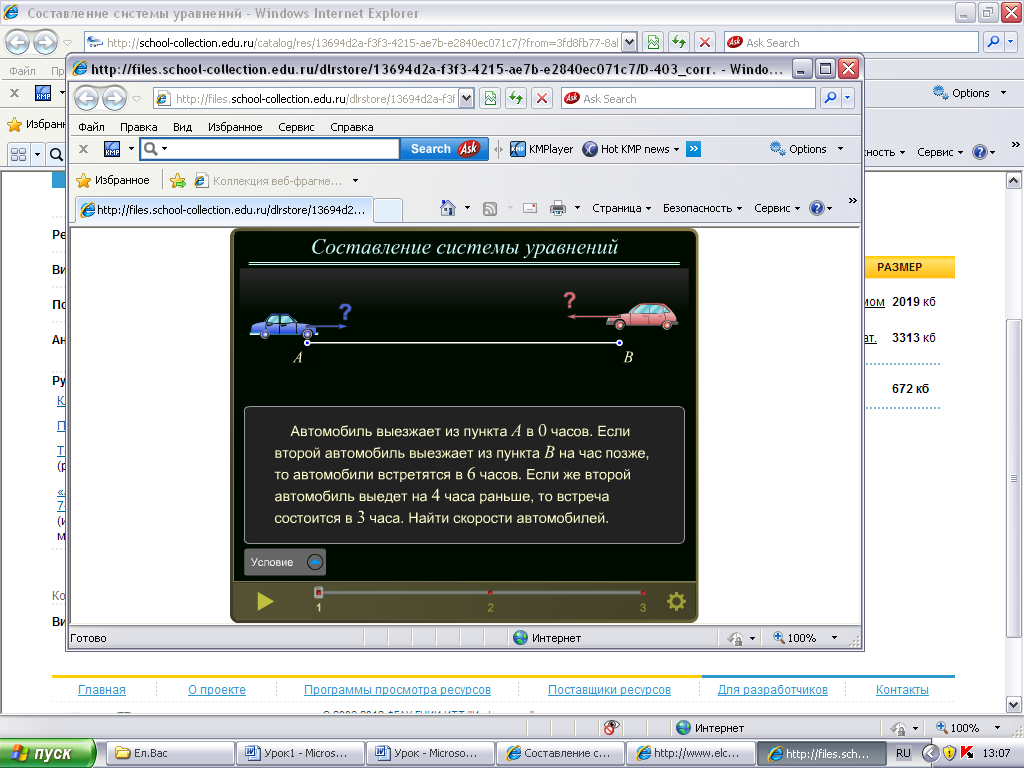 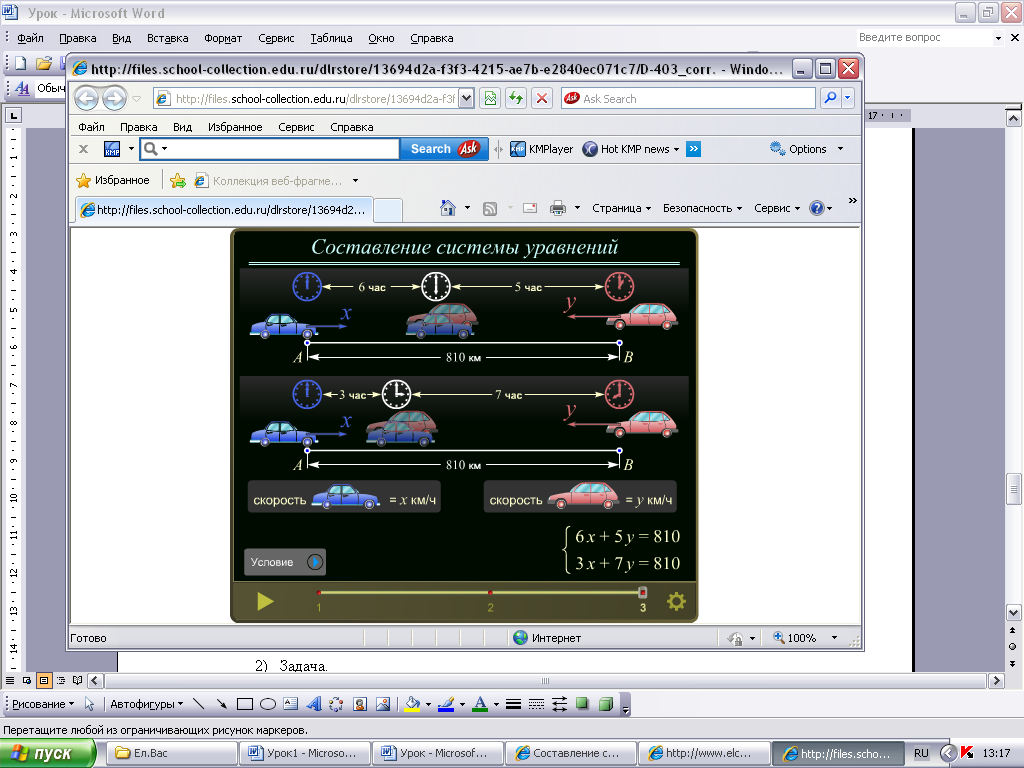 IV. Включение в систему знаний и повторение. Организация работы учащихся на тренировку ранее изученных алгоритмов, включение нового знания в систему знаний. Решим данную систему двумя способами. Первый способ: метод подстановки 6х + 5у = 810, у = 162 – 1,2х, х = 60, 3х + 7у = 810; 3х + 7(162 – 1,2х) = 810; у = 90. Второй способ: метод алгебраического сложения 6х + 5у = 810, 6х + 5у = 810, -9у = -810, х = 60, 3х + 7у = 810; -6х – 14у = -1620; 3х + 7у = 810; у = 90. Вывод: каким способом удобнее решить эту систему? V. Закрепление.
Задача Как-то лошадь и мул вместе вышли из дома, Их хозяин поклажей большой нагрузил, Долго-долго тащились дорогой знакомой, Из последней уже выбиваяся сил. «Тяжело мне идти» - лошадь громко стенала. Мул с иронией молвил (нес он тоже немало): «Неужели, скажи, я похож на осла? Может, я и осел, но вполне понимаю: Моя ноша значительно больше твоей. Вот представь: я мешок у тебя забираю, И мой груз стал в два раза, чем твой, тяжелей. А вот если тебе мой мешок перебросить, Одинаковый груз наши спины б согнул». Сколько ж было мешков у страдалицы-лошади? Сколько нес на спине умный маленький мул?
Решение: 2(х – 1) = у + 1, 2х – у = 3, х = 5, х + 1 = у – 1; х – у = -2; у = 7. Ответ: лошадь несла 5 мешков, мул – 7 мешков.
Решение задач при помощи систем линейных уравнений, К2. (модуль с пошаговым контролем, состоящим из двух шагов).
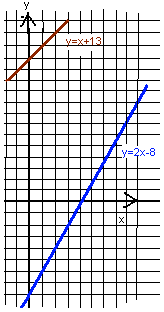
На каких уроках вы уже встречались со словом система уравнений? Рефлексия деятельности. Организация самооценки учениками деятельности на уроке. Чем занимались на уроке? Что понравилось? Что, по-вашему, не удалось? Домашнее задание: § 14, № 14.5; № 14.8 Фрагмент урока № 1. Метод подстаноки п. 12. Цель урока: Повторить правила раскрытия скобок, приведения подобных и решения линейных уравнений. Ввести правило решения системы методом подстановки. Формировать умение решать системы линейных уравнений методом подстановки. Ход урока I. Организационный момент. II. Актуализация знаний. Устно (с использованием мультимедийной презентации). № 1. Раскрыть скобки: 1) 2) 3) 4) № 2. Привести подобные: 1) 2) 3) 4) № 3. Решить уравнение: 1) 2) III. Практическая работа: решить систему уравнений графическим способом.
IV. Проверка практической работы:
Вывод: для решения данных уравнений графический способ не удобен: в варианте 1решением являются дробные числа, определить которые по графику трудно: в варианте 2 решением являются большие числа, для определения которых не достаточно страницы тетради. Для решения данных систем необходим другой способ решения. V. Изучение нового материала (с использованием мультимедийной презентации). 1. Решение системы уравнений. №12.2(а,б),12.5(а,б) 2. Составление алгоритма решения систем уравнений методом подстановки. 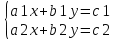 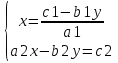 a2  ) + b2y=c2 ) + b2y=c2
VI. Решение систем способом подстановки: Используемые ЦОР
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||