Урок математики (алгебры) по теме: «Решение задач с помощью систем уравнений второй степени»
 Скачать 44.65 Kb. Скачать 44.65 Kb.
|
| Урок математики (алгебры) по теме: «Решение задач с помощью систем уравнений второй степени». Бойкова Антонина Станиславовна, учитель математики. Статья отнесена к разделу: Преподавание математики. Цель урока: сформулировать умение решать задачи составлением систем уравнений; воспитание уважительного отношения к сверстникам; развивать навыки само и взаимоконтроля. Форма проведения урока: комбинированный урок. Оборудование: раздаточный материал. Ход урока. План урока.
1.Организационный момент. Вместе с дежурными учитель проверяет готовность класса к уроку, Учащимся сообщается тема, цели и задачи урока. Работа «слабых» учащихся будет организована по карточкам-консультантам. 2.Проверка домашнего задания. Проверка домашнего задания осуществляется в виде самостоятельной работы по вариантам. При решении учащиеся 1 и 2 вариантов могут воспользоваться карточками- консультантами. 1 вариант Решите систему уравнений: 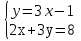 ; ;Ответ: x = 1; y = 2. 2 вариант Решите систему уравнений: 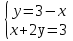 ; ;Ответ: x = 3; y = 0. 3 вариант Решите систему уравнений: 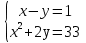 ; ;Ответ: ( -7; -8 ); ( 5; 4 ). Карточки-консультанты: 1вариант 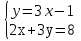 ; ;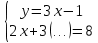 ; ;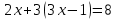 , ,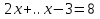 , ,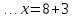 , ,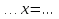 , ,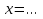 , ,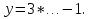 Ответ: … 2 вариант. 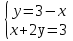 ; ;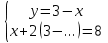 ; ;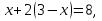 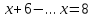 , ,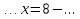 , ,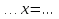 , ,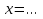 , ,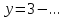 , ,Ответ: … . 3.Математический диктант. Ученики делают диктант под копировку. Копию работы оставляют себе для самопроверки. Два ученика выполняют диктант у доски по вариантам. 1вариант. Составьте уравнение с двумя переменными, если:
2 вариант Составьте уравнение с двумя переменными, если:
4. Решение задач. Для подготовки учащихся к решению задач повторяются и систематизируются их знания. Решение задач состоит из трёх этапов:
Каждый из этих этапов является важным в решении задачи. Ученик решает на доске № 272. [1] Пусть x м – длина участка, y м – ширина участка, ( 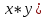 м – площадь участка. м – площадь участка.2(x + y ) м – длина изгороди участка. Зная, что xy =2400, а 2( x + y ) = 200, то составим и решим систему уравнений: 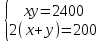 ; ;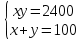 ; ;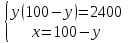 ; ;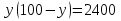 , ,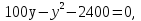 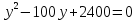 , ,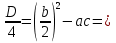 2500 – 2400=100, D 2500 – 2400=100, D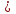 0, 2 корня, 0, 2 корня,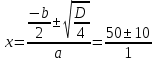 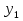 =60; =60; 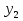 =40. =40.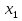 =100 – 60 = 40, =100 – 60 = 40,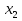 =100 – 40 = 60. =100 – 40 = 60.Ответ: 60 м, 40 м. 5.Самостоятельная работа. При решении работы учащиеся могут воспользоваться карточками-консультантами. 1 вариант. Разность двух чисел равна 5, а их произведение 84. Найдите эти числа. 2 вариант. Разность двух натуральных чисел равна 24, а их произведение равно 481. Найдите эти числа. Карточки-консультанты к самостоятельной работе. 1 вариант Пусть x – первое число, y – второе число. Зная, что x-y – разность чисел, x-y = …, xy – произведение чисел, xy = …, то составим и решим систему уравнений: 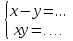 2 вариант. Пусть x- натуральное число, y- второе натуральное число. Зная, что x-y-разность чисел, x-y =…, xy - произведение чисел, xy =…, то составим и решим систему уравнений: 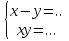 6.Итог урока. В конце урока оцениваются ответы учащихся у доски и самостоятельные работы. Ещё раз обращается внимание учащихся на 3 этапа решения данных задач. 7.Задание на дом. № 581,583,585 (составить системы уравнений). [1] Список литературы: 1. Учебник для 9 класса общеобразовательных учреждений/ Ю. Н. Макарычев, Н. Г. Миндюк, К. И. Нешков, С. Б. Суворов; Под редакцией С. А. Теляковского.- М.: Просвещение, 1995. |