§13. Произведение синусов и косинусов.
Лекция, решение задач
|
Применение формул замены произведения синусов и косинусов при вычислениях и преобразованиях.
|
Зная основные тригонометрические тождества, могут совершать преобразования простых тригонометрических выражений. Умеют составлять текст научного стиля (П)
|
Зная основные тригонометрические тождества, могут совершать преобразования сложных тригонометрических выражений. Могут собрать материал для сообщения по заданной теме (ТВ)
|
|
|
|
|
|
Урок обобщения и систематизации знаний.
|
КУ
|
Организация совместной учебной деятельности
|
Учащихся консультируются у учителя по вопросам данной темы, владеют навыками самоанализа и самоконтроля, готовятся к контрольной работе
|
|
|
|
|
|
Контрольная работа №7
|
КР
|
Самостоятельное планирование и проведение исследования решения
|
Учащихся демонстрируют: систематические сведения на практической работе.
|
Учащиеся могут свободно применять теоретические знания и умения на практической работе.
|
КР
|
|
|
|
|
§1. Уравнение
cosх =a.
|
Лекция, решение упражнений
|
Знакомство с понятием арккосинуса числа, обучение решению простейших тригонометрических уравнений.
|
Имеют представление об арккосинусе, арксинусе и могут решать простейшие уравнения 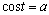 . Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (Р) . Умеют объяснить изученные положения на самостоятельно подобранных конкретных примерах. (Р)
|
Могут строить график арккосинуса, арксинуса и решать неравенства 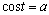 .Умеют работать с учебником, отбирать и структурировать материал. (И) .Умеют работать с учебником, отбирать и структурировать материал. (И)
|
|
|
|
|
|
Уравнение cosх =a.
|
Практикум
|
Решение уравнений вида cosх =a и сводящихся к ним.
|
Могут решать простейшие тригонометрические уравнения по формулам. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
|
|
|
|
|
|
Уравнение cosх =a. Самостоятельная работа
|
Практикум, СР
|
|
|
|
СР
|
|
|
|
|
§2. Уравнение sinx=а.
|
Лекция, решение упражнений
|
Знакомство с понятием арксинуса числа, обучение решению простейших тригонометрических уравнений.
|
Могут решать простейшие тригонометрические уравнения по формулам. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
|
|
|
|
|
|
Уравнение sinx=а.
|
Практикум
|
Решение уравнений вида sinx=а.и сводящихся к ним
|
|
|
|
|
|
Уравнение sinx=а. Самостоятельная работа
|
Практикум, СР
|
|
СР
|
|
|
|
|
§3. Уравнение tgx=а. Уравнение ctgx=а.
|
Лекция, решение уравнений
|
Знакомство с понятием арктангенса числа, обучение решению простейших тригонометрических уравнений вида tgx=а и ctgx=а.
|
Знают определение арктангенса. арккотангенса и могут решать простейшие уравнения 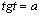 и и 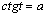 . Умеют определять понятия, приводить доказательства. (П) . Умеют определять понятия, приводить доказательства. (П)
|
Могут строить график арктангенса, арккотангенса и решать неравенства 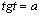 и и 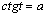 . Умеют передавать, информацию сжато, полно, выборочно. (И) . Умеют передавать, информацию сжато, полно, выборочно. (И)
Могут решать сложные тригонометрические уравнения, сводящиеся к простейшим.
|
|
|
|
|
|
Уравнение tgx=а. Уравнение ctgx=а.
|
Практикум
|
Решение уравнений вида tgx=а и ctgx=а и сводящихся к ним.
|
Могут решать простейшие тригонометрические уравнения по формулам. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
|
|
СР
|
|
|
|
|
§4. Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения.
|
КУ
|
Решение тригонометрических уравнений, сводящихся к алгебраическим, а также решению однородных уравнений первой и второй степеней.
|
Могут решать простейшие тригонометрические уравнения по формулам. Могут объяснить изученные положения на самостоятельно подобранных конкретных примерах. (П)
|
|
|
|
|
|
|
Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения.
|
КУ
|
Решение тригонометрических уравнений, сводящихся к алгебраическим, а также решению однородных уравнений первой и второй степеней.
|
|
|
|
|
|
|
Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения.
|
КУ
|
Решение тригонометрических уравнений, сводящихся к алгебраическим, а также решению однородных уравнений первой и второй степеней.
|
Знают, как решать простейшие тригонометрические уравнения по формулам. Умеют извлекать необходимую информацию из учебно-научных текстов. Могут найти и устранить причины возникших трудностей. (Р)
|
|
|
|
|
|
|
Тригонометрические уравнения, сводящиеся к алгебраическим. Однородные и линейные уравнения. Самостоятельная работа
|
КУ, СР
|
Решение тригонометрических уравнений, сводящихся к алгебраическим, а также решению однородных уравнений первой и второй степеней.
|
Могут решать однородные тригонометрические уравнения первой степени. Могут привести примеры, подобрать аргументы, сформулировать выводы. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (П)
|
|
СР
|
|
|
|
|
§5. Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения.
|
КУ
|
Расширение знаний учащихся о применимости метода замены обозначения в тригонометрии, с оценочным методом при решении тригонометрических уравнений.
|
Знают, как решать тригонометрические уравнения данными методами. Умеют извлекать необходимую информацию из учебно-научных текстов. Могут найти и устранить причины возникших трудностей. (Р)
Могут привести примеры, подобрать аргументы, сформулировать выводы. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (П)
|
Учащиеся профильных классов должны знать особенности метода замены универсальной тригонометрической подстановки при решении тригонометрических уравнений
|
|
|
|
|
|
Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения.
|
|
|
|
|
|
Методы замены неизвестного и разложения на множители. Метод оценки левой и правой частей тригонометрического уравнения.
|
КУ
|
Расширение знаний учащихся о применимости метода замены обозначения в тригонометрии, с оценочным методом при решении тригонометрических уравнений.
|
СР
|
|
|
|
|
§6. Системы тригонометрических уравнений.
|
КУ
|
Знакомство с приемами решения систем тригонометрических уравнений.
|
Могут решать системы тригонометрических уравнений первой степени. Могут привести примеры, подобрать аргументы, сформулировать выводы. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (П)
|
|
Индивидуальный опрос
|
|
|
|
|
Системы тригонометрических уравнений.
|
КУ
|
Решение систем тригонометрических уравнений
|
Фронтальный опрос,СР
|
|
|
|
|
§7. Тригонометрические неравенства.
|
Лекция, решение упражнений
|
Знакомство с приемами решения простейших тригонометрических неравенств с помощью единичной окружности.
|
Знают, как решать тригонометрические неравенства. Умеют извлекать необходимую информацию из учебно-научных текстов. Могут найти и устранить причины возникших трудностей. (Р)
Могут привести примеры, подобрать аргументы, сформулировать выводы. Могут излагать информацию, интерпретируя факты, разъясняя значение и смысл теории. (П)
|
|
Индивидуальный опрос
|
|
|
|
|
Тригонометрические неравенства.
|
Практикум
|
Решение тригонометрических неравенств.
|
Фронтальный опрос
|
|
|
|
|
Урок обобщения и систематизации знаний.
|
КУ
|
Организация совместной учебной деятельности
|
Учащихся консультируются у учителя по вопросам данной темы, владеют навыками самоанализа и самоконтроля, готовятся к контрольной работе
|
|
|
|
|
|
Контрольная работа №8 по теме «Тригонометрические уравнения и неравенства»
|
КР
|
|
Учащихся демонстрируют умение расширять и обобщать сведения о видах тригонометрических уравнений; умение решения разными методами тригонометрических уравнений (П)
|
Могут самостоятельно выбрать метод решения тригонометрического уравнения. Владеют навыками самоанализа и самоконтроля. (ТВ)
|
КР
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
 Скачать 0.58 Mb.
Скачать 0.58 Mb.