«Решение простейших тригонометрических уравнений»

Название	«Решение простейших тригонометрических уравнений»
Дата	12.02.2016
Размер	92.09 Kb.
Тип	Документы

УПРАВЛЕНИЕ ОБРАЗОВАНИЯ ГОРОДА ТУЛЫ

МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ-

МУНИЦИПАЛЬНАЯ ОЩЕОБРАЗОВАТЕЛЬНАЯ

СРЕДНЯЯ ШКОЛА № 33 ИМЕНИ Л.П.ТИХМЯНОВА

Г. Тула ул. С. Перовской, д. 40 тел/ факс 8(4872) 31-81-40

РАЗРАБОТКА ОТКРЫТОГО УРОКА

по алгебре и началам анализа

в 10 классе

по теме

«Решение простейших тригонометрических уравнений ».

Учитель: Панина Елена Юрьевна

Цели урока:

Образовательные:

Актуализировать знания учащихся по теме «Решение простейших тригонометрических уравнений» и обеспечить их применение при решении задач вариантов ЕГЭ;
Повторить, углубить, обобщить и систематизировать приобретенные знания по теме « Решение простейших тригонометрических уравнений» для дальнейшего использования при решении тригонометрических уравнений.

Развивающие:

Содействовать развитию у учащихся мыслительных операций: умение анализировать, синтезировать, сравнивать;
Формировать и развивать общеучебные умения и навыки: обобщение, поиск способов решения;
Отрабатывать навыки самооценивания знаний и умений, выбора задания, соответствующего их уровню развития.

Воспитательные:

Вырабатывать внимание, самостоятельность при работе на уроке;
Способствовать формированию активности и настойчивости, максимальной работоспособности;
Развивать интерес к урокам математики.

Тип урока:

урок обобщения и систематизации знаний.

Оборудование:

компьютер и мультимедийный проектор.

Технологии:

технология дифференциального обучения;

технология применения средств ИКТ;

игровая технология.

Структура урока:

1. Вводно-мотивационная часть.

1.1. Организационный момент.

2. Основная часть урока.

2.1 Проверка домашнего задания: фронтальный опрос, демонстрация решения на доске, устная работа.

2.2. Проверка усвоения знаний, умений и навыков при решении простейших тригонометрических уравнений (чередование фронтальной и индивидуальной форм работы с последующей проверкой задания).

2.3. Устная работа с классом.

3. Рефлексивно-оценочная часть урока.

3.1. Подведение итогов урока.

3.2. Обсуждение результатов индивидуальной работы.

3.3. Информация о домашнем задании.

подготовить учащихся к работе на уроке;
взаимное приветствие;
проверка подготовленности учащихся к уроку ( рабочее место, внешний вид);
организация внимания.

Установить правильность выполнения домашнего задания всеми учащимися.

Вопрос учащимся: какие трудности возникли при выполнении домашнего задания?

Разобрать у доски пример по № 3, 5.

Вопрос учащимся: Какое слово у вас получилось?

Домашнее задание: Найти соответствие и записать полученное слово.

п/п	Решить уравнения	Буквы	Ответы
	cos 2x = √2/2	А	πn, nЄZ
	5sin x = 6	О	(-1)arcsin 6/5 + πn, nЄZ
	sin ( π/3 - 3x/5 ) = √3/2	Ы	нет решений
	2cos ( - x/2 ) = -√2	К	±3π/2 + 4πn, nЄZ
	tg ( x+π/4 ) = 1	М	(-1) ( -5π/9 ) + 5π/9 + 5/3πn, nЄZ
		Ш	± π/8+πn, nЄZ
		В	± arccos(-1) + 2πn, nЄZ

Решение домашнего задания:

cos 2x = √2/2

РЕШЕНИЕ:

2
М
x = ± arccos√2/2 + 2πn, nЄZ;

2x = ± π/4 + 2πn, nЄZ;

x = ± π/8 + πn, nЄZ;

ОТВЕТ: x = ± π/8 + πn, nЄZ. (М).

2. 5sin x = 6

Р
Ы
ЕШЕНИЕ:

sin x = 6/5;

решений нет

ОТВЕТ: решений нет (Ы).
3. sin ( π/3 - 3x/5 ) = √3/2

РЕШЕНИЕ:

Ш
- sin ( 3x/5 - π/3 ) = √3/2;

sin ( 3x/5 - π/3 ) = - √3/2;

3x/5 - π/3 = (-1) arcsin ( -√3/2 ) + πn, nЄZ ;

3x/5 - π/3 = (-1) ( - π/3 ) + πn, nЄZ ;

3x/5 = (-1) ( - π/3 ) + π/3 + πn, nЄZ ;

3x = (-1) ( - 5 π/3 ) + 5π/3 + 5πn, nЄZ ;

x = (-1) ( - 5 π/9 ) + 5π/9 + 5/3 π n, nЄZ ;

ОТВЕТ: x = (-1) ( - 5 π/9 ) + 5π/9 + 5/3 π n, nЄZ.(Ш)

2cos ( - x/2 ) = -√2

РЕШЕНИЕ:

2

cos ( x/2 ) = -√2;

c
К
os ( x/2 ) = -√2/2;

x/2 = ± arccos (-√2/2) + 2πn, nЄZ;

x/2 = ± ( π - π/4 ) + 2πn, nЄZ;

x/2 = ± 3π/4 + 2πn, nЄZ;

x = ± 3π/2 + 4πn, nЄZ;

ОТВЕТ: x = ± 3π/2 + 4πn, nЄZ. (К)
5. tg ( x + π/4 ) = 1

РЕШЕНИЕ:

А
x + π/4 = π/4+πn, nЄZ;

x = π/4 - π/4 +πn, nЄZ;

x = πn, nЄZ;

ОТВЕТ: x = πn, nЄZ;(А)
Полученное слово:

Двое учащихся работают по карточкам на первых партах.

Решите уравнения:

sin x /2 = 1 ;
cos 2x + 2 = 0;
cos ( 3x - π/3 ) = - 1/2;

Найти: arcsin ( - ½ ).
Решите уравнения:

cos 2x + 2 = 0;
sin 1/5 x = 1 ;
2 sin ( x + π/6 ) - √3 = 0;

Найти: arccos(-1)

Задание: выбрать правильный ответ

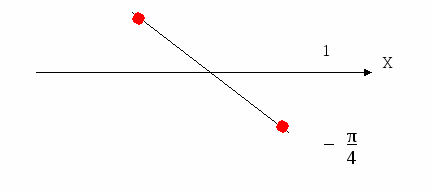
s
3
in x = -1 1. - π/2 +πn, nЄZ;

2. π + 2πn, nЄZ;

3. - π/2 + 2πn, nЄZ;

4. ( - 1 ) π/2 + πn, nЄZ.
ОТВЕТ: 3.

Решите уравнение:

а).cos x = √3;

Ответ: нет решений.

б). tg x = - √3;

Ответ: - arctg√3 + πn, nЄZ .

Найти: arccos ( -√2/2 )

Ответ: π - π/4 = 3π/4.

Найти область определения и область значений у = сtg x.

Ответ: область определения: х = πn;

область значений: R

1. Один учащийся решает у доски вместе с классом
Решите уравнение:

2cos ( x/2 - π/6 ) + √2 = 0.
РЕШЕНИЕ:
2cos ( x/2 - π/6 ) = -√2;

cos ( x/2 - π/6 ) = -√2/2;

x/2 - π/6 = ± arccos (-√2/2) + 2πn, nЄZ;

x/2 - π/6 = ± ( π - π/4 ) + 2πn, nЄZ;

x/2 - π/6 = ± 3π/4 + 2πn, nЄZ;

x/2 = ± 3π/4 + π/6 + 2πn, nЄZ;

x = ± 3π/2 + π/3 + 4πn, nЄZ.
ОТВЕТ: x = ± 3π/2 + π/3 + 4πn, nЄZ.
2. Двое учащихся решают уравнения на доске ( на скрытой). Класс решает эти задания по вариантам.

1 вариант	2 вариант
tg (3x + π/4 ) +1 = 0. РЕШЕНИЕ: tg (3x + π/4 ) = -1; 3x + π/4 = -π/4 + πn, nЄZ; 3x = -π/4 - π/4 + πn, nЄZ; 3x = -π/2 + πn, nЄZ; x = -π/6 + π/3n, nЄZ; ОТВЕТ:x = -π/6 + π/3n, nЄZ.	2cos ( 2x/3 + π/3 ) = √2; РЕШЕНИЕ: cos ( 2x/3 + π/3 ) = √2/2; 2x/3 + π/3 = ± arccos (√2/2) + 2πn, nЄZ; 2x/3 + π/3 = ± π/4 + 2πn, nЄZ; 2x/3 = ± π/4 - π/3 + 2πn, nЄZ; 2x = ± 3π/4 - π + 6πn, nЄZ; x = ± 3π/8 - π/2 + 3πn, nЄZ. ОТВЕТ: x = ± 3π/8 - π/2 + 3πn, nЄZ.

Класс сверяет свои решения с решением на доске.

3.Один учащийся у доски решает вместе с классом

Задание :выберите правильный ответ:

Решить уравнение

Ответы

( cos ( x + π/4 ) - 1 ) ( sin ( x - π/4 ) – 1 ) = 0;
РЕШЕНИЕ:
cos ( x + π/4 ) - 1 = 0 или sin ( x - π/4 ) – 1 = 0

cos ( x + π/4 ) = 1, sin ( x - π/4 ) = 1

x + π/4 = 2πn, nЄZ x - π/4 = π/2 + 2πn, nЄZ

x = - π/4 + 2πn, nЄZ x = π/2 + π/4 + 2πn, nЄZ

x = 3π/4 + 2πn, nЄZ

Объединяем решения : - π/4 + πn, nЄZ

У

3π

4

ОТВЕТ: 3.

π/4 + 2πn, nЄZ
3π/4 + 2πn, nЄZ
- π/4 + πn, nЄZ
- π/4 + 2πn, nЄZ

Это уравнение позволяет отработать навыки объединения двух серий корней и записывать в виде одной.
4. Решить уравнение: 2 cos ( π/6 - x/3 ) – 1 = 0;
РЕШЕНИЕ:

2 cos ( π/6 - x/3 ) = 1 ;

2 cos ( x/3 - π/6 ) = 1;

cos ( x/3 - π/6 ) = 1/2;

x/3 - π/6 = ± arccos 1/2 + 2πn, nЄZ;

x/3 - π/6 = ± π/3 + 2πn, nЄZ;

x/3 = ± π/3 + π/6 + 2πn, nЄZ;

x = ± π + π/2 + 6πn, nЄZ;
ОТВЕТ: x = ± π + π/2 + 6πn, nЄZ.
5. Решить уравнение: 4 cos ( x/4 + π/6 ) = √3;
РЕШЕНИЕ:
cos ( x/4 + π/6 ) = √3/4;

x/4 + π/6 = ± arccos (√3/4) + 2πn, nЄZ;

x/4 = ± arccos √3/4 - π/6 + 2πn, nЄZ;

x = ± 4 arccos √3/4 - 2π/3 + 8πn, nЄZ;
ОТВЕТ: x = ± 4 arccos √3/4 - 2π/3 + 8πn, nЄZ.

6. Решить уравнение: - 2cos ( - πх/4 ) = √2;
РЕШЕНИЕ:
- 2cos πх/4 = √2;

cos (πх/4) = -√2/2 ;

πх/4 = ± arccos (-√2/2 ) + 2πn, nЄZ;

πх/4 = ± ( π - arccos √2/2 ) + 2πn, nЄZ;

πх/4 = ± ( π - π/4) + 2πn, nЄZ;

πх/4 = ±3π/4 + 2πn, nЄZ;

πх = ±3π + 8πn, nЄZ;

х = ±π + 8n, nЄZ;
ОТВЕТ: х = ±π + 8n, nЄZ.

7. Решить уравнение: - 2 sin ( 3x/4 - π/3 ) + 1 = 0
РЕШЕНИЕ:

- 2 sin ( 3x/4 - π/3 ) = - 1;

2 sin ( 3x/4 - π/3 ) = 1;

sin ( 3x/4 - π/3 ) = 1/2;

3x/4 - π/3 = (-1) arcsin ( 1/2 ) + πn, nЄZ ;

3x/4 - π/3 = (-1) π/6 + πn, nЄZ ;

3x/4 = (-1) π/6 + π/3 + πn, nЄZ ;

3x = (-1) 2π/3 + 4π/3 + 4πn, nЄZ ;

x = (-1) 2π/9 + 4π/9 + 4/3πn, nЄZ ;
ОТВЕТ: x = (-1) 2π/9 + 4π/9 + 4/3πn, nЄZ.

Учитель комментирует выставленные на уроке оценки. Для домашнего задания учащимся были розданы карточки с дифференцируемым заданием.

Уравнения на « 3 »
	sin x = - √3/2
	cos x/2 = - √2/2
	2sin x - √3 = 0
	ctg(x –π/3 ) = √3
	tg 4x = - √3
Уравнения на « 4 »
	2cos x + √2 = 0
	sin ( 2x - π/3 ) + 1 = 0
	sin (2 π - x ) – cos ( 3 π/2 + x ) = -1
	3tg 4x = √3
	4sin π/6 cos (x + π/3 ) = - √3
Уравнения на « 5 »
	sin ( 2 π – x) – cos( 3π/2 + x ) = - 1
	-2 cos ( - πx/4 ) = √2
	sin( x - π/4 ) ( sin 2x +√2 ) = 0
	2sin ( π/6 – x/2 ) + 1 = 0
	( cos 3x + 1 ) cos x/2 = 0