Деятельность учителя
|
Деятельность обучающихся
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности.
|
1.Этап урока (орг.момент 2 мин.).
|
-приветствие ученика;
-перед уроком учитель загружает УМК «Живая математика»;
-включает демонстрацию экрана;
-сообщение темы урока: «Арккосинус и решение уравнения cos t = a».
Перед изучением новой темы необходимо повторить материал, изученный ранее.
|
-перед уроком ученик загружает УМК «Живая математика» и отправляет файлы с дом. работой.
|
|
Приветствие учителя.
Подготовка к совместной работе с учителем в программе «Живая математика».
|
|
Проверка готовности к уроку.
|
Настрой на добычу новых знаний. Ответственность за знания.
|
2.Этап урока (актуализация знаний 5 мин. ).
|
Деятельность учителя
|
Деятельность обучающихся
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности.
|
Проверка дом практической работы(граф. Планшет).
|
дом. практическую работу (графики тригонометрических функций). ( «ЖМ» ).
|
исправление ошибок в дом.работе с помощью граф.планшета.
|
Совместная работа с учителем в программе «Живая математика», исправление ошибок в дом.работе с помощью граф.планшета.
|
Самоконтроль и контроль действий партнёра.
|
Исправление ошибок.
|
Умение различать верный способ действия.
|
Определите координаты точек, значения
cos t и sin t :
Р п/3
Р п/2
Р п
Р п/4
Р- п/3
Р -п/2
Р -п
Р- п/4
|
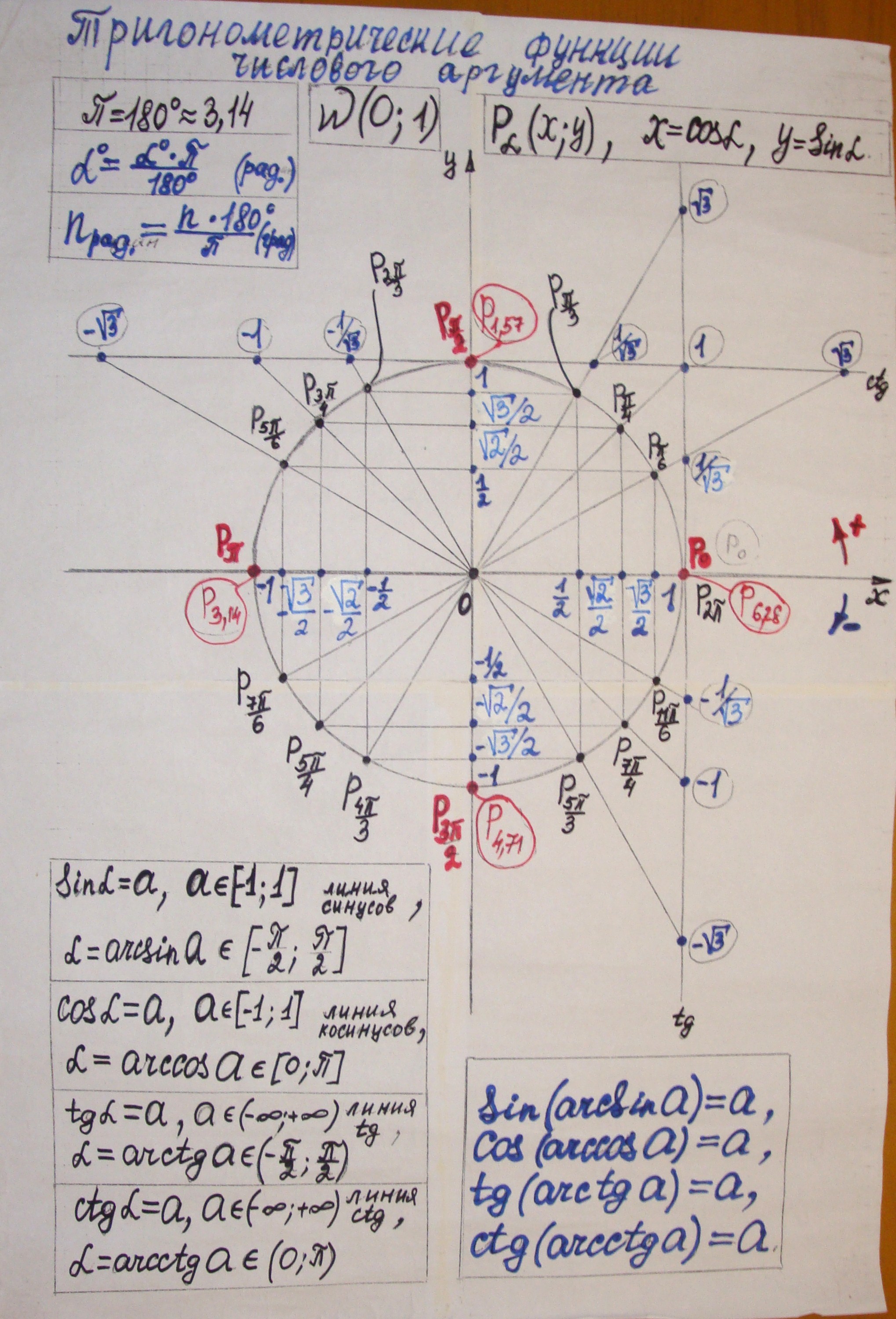
Отвечает на поставленный вопрос, если возникают трудности, то повторяем числовую окружность, где находятся значения тригонометрических функций на числовой окружности, их периодичность.
|
Использование числовой окружности при нахождении значений тригонометрических функций числового аргумента.
|
Отвечает на поставленный вопрос, если возникают трудности, то учитель может прийти на помощь (задав очередной вопрос).
|
Самоконтроль и контроль действий партнёра ( со стороны учителя всегда возможен подвох).
|
Внимательно следить за (дорогой) ходом урока
|
Умение различать верный способ действия.
|
Используя числовую окружность,найти значение t:
cos t = 0,
cos t = ½ ,
cos t = 3, t=
cos t = - ¾, t=
cos t = -1,
cos t = √3/2,
cos t = ¾, t=
cos t = -√3/2,
cos t = −½,
cos t = 2/5.
cos t = - √2/2,
cos t = 1,
cos t = −5, t=
cos t = √2/2,
cos t = - 2/5.
|
Ответ ученика:
cos t = 0,
t= +п/2; - п/2
cos t = ½ t= +п/3; - п/3
cos t = 3, t=
cos t = - ¾, t=
cos t = -1,
t=+ п ; - п
cos t = √3/2, t=+п/6; - п/6
cos t = ¾, t=
cos t = -√3/2, t=+5п/6; - 5п/6
cos t = −½, t=+2п/3; - 2п/3
cos t = 2/5.
cos t = - √2/2,
t= +3 п/4: -3 п/4
cos t = 1, t=0
cos t = −5, t=
cos t = √2/2, t=+п/4; - п/4
cos t = - 2/5, t =
|
Не забываем + 2Пк, где к-целое .
Найти ошибки в записи.
Использование числовой окружности при нахождении значений тригонометрических функций числового аргумента и обратно нахождение числового аргумента для заданных значений тригонометрических функций.
Умение решать и формулировать прямую и обратную задачи.
|
Отвечает на поставленный вопрос, если возникают трудности, то учитель может прийти на помощь (задав очередной вопрос).
|
Самоконтроль и контроль действий партнёра ( со стороны учителя всегда возможен подвох).
|
Внимательно следить за (дорогой) ходом урока
|
Умение различать верный способ действия. Умение доказывать свою точку зрения.
|
3. Этап урока (создание проблемной ситуации 5 мин.).
|
1) Что это за число t,
при котором
cos t = 2/5,
cos t = -2/5,
cos t = ¾ ,
cos t = - ¾ ?
2) Как же решается уравнение вида
cos t = а?
|
Имеющиеся знания не позволяют дать ответ , а новых пока не добыл.???????
|
Ученик сам формулирует проблему, или вопросы на которые должен найти ответ.
|
Учитель приходит на помощь ученику, если возникают трудности.
|
Совместная работа позволяет сформулировать проблему.
|
Внимательно следить за (дорогой) ходом урока
|
Умение различать верный способ действия. Умение доказывать свою точку зрения.
|
4. Этап урока ( физ. минутка 2 мин.).
|
5. Этап урока (выдвижение гипотезы 5 мин.).
|
Деятельность учителя
|
Деятельность обучающихся
|
Познавательная
|
Коммуникативная
|
Регулятивная
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности
|
Осуществляемые действия
|
Формируемые способы деятельности.
|
Разрешимо ли это уравнение?
|
Ведь на линии косинусов есть значение 2/5, значит и решение уравнения существует, как записать его?
|
Выдвижение гипотезы.Умение обобщать, анализировать, высказывать своё мнение. Формулировка определения.
|
Умение повести за собой при решении возникшей проблемы, умение слушать другого. Формулировка определения с помощью учителя.
|
Убедить участников в верности выбранного пути, умение слушать другого. Уточнения в определении.
|
Внимательно следить за (дорогой) ходом урока
|
Умение различать верный способ действия.
|
Ввожу новое понятие.
Арккосинус
двух пятых (arcus в переводе с латинского значит дуга-арка)
|
Длина дуги числовой окружности равна arccos 2/5 .
|
arccos 2/5
(arc)-математический знак,
cos t - исходная функция,
2/5 напоминание о правой части уравнения
cos t = 2/5.
|
+ arccos 2/5 ,
- arccos 2/5 .
|
Определение:
если│а│≤ 1, то
arccos a = t ↔
{ cos t = a, 0 ≤ t ≤ П.
arccos a - это такое число из отрезка [0;П], косинус которого равен а.
|

|
6. Этап урока (поиск решения проблемы 15мин.).
|
Решить уравнение:
cos t = 2/5,
cos t = - 2/5,
cos t = 3,
cos t = −5,
cos t = 1,
cos t = -1,
cos t =0.
cos t = a,
Все ли корни уравнения указаны?
Будет ли корнем уравнения корень
arccos( 0,5) + 2п;
arccos( 0,5) + 22п;
arccos( 0,5) — 12п;
|
cos t = 2/5.
t =+-arccos 2/5 + 2Пк, где к-целое.
cos t = - 2/5.
t =+-arccos( -2/5) + 2Пк, где к-целое.
Решений нет.
Решений нет.
t = 2Пк, где к-целое.
t = П + 2Пк, где к-целое .
t = П/2 + 2Пк, где к-целое .
t =+-arccos a + 2Пк, где к-целое.
|
Умение объяснить , как решаются уравнения и почему так?
Как работает определение
arccos a = t
при решении уравнений вида
cos t = a ?
|
Учитель приходит на помощь ученику, если возникают трудности или специально создаёт их.
|
Умение сказать нет и доказать свою правоту.
|
Внимательно следить за (дорогой) ходом урока
|
Умение различать верный способ действия.
|
Проблема решена!!!!
|
7. Этап урока. (проверка найденного решения (6 мин.).
|
Решить уравнения:
cos t = - ¾,
cos t = ¾.
Найти значение выражения:
arccos 0,5,
arccos 5/2,
arccos 0
cos t = ¾,
arccos (-1)
|
Самостоятельная работа (презентация).
|
Имеет представление об арккосинусе и умеет решать уравнение cos t = a, используя презентацию.
|
Использование презентации учителя при решении уравнений.
|
Создание в будущем своей презентации по данной теме.
|
Умение воспользоваться определением
arccos a = t при решении уравнений вида
cos t = a .(презентация).
|
Оценивать правильность выполненных действий.
|
8. Этап урока (итоги урока 5 мин.).
|
Домашнее задание: глава3,§15,
№15.1-№15.7(в,г); оценка за урок; постановка проблемы на следующий урок.
|
|
|
|
|
|
|
Проблема, поставленная в перспективу: Как же решается уравнение вида
sin t = а?
|
Ученик подводит итог урока, отвечая на вопросы;
1) решены ли проблемы, поставленные в начале урока;
2) какие новые знания открыл для себя на уроке;
3) применение новых знаний при решении задач.
|
В результате ответственного и самостоятельного принятия решений и самоанализа научились решать уравнения вида
cos t = a.
Скованность и неуверенность ребёнка исчезли.
Ребёнок сам добыл знания.
|
|
|
|
|
Рефлексия: ученик заинтересовался поставленной перед ним проблемой – всё прекрасно, знания будут; не заинтересовался – заинтересуем на следующем уроке.
|
 Скачать 167.44 Kb.
Скачать 167.44 Kb.
