|
воздуховод квадратный Мы занимаемся изготовлением как типовых пластиковых баков, так и резервуаров произвольной формы по желанию заказчика. Конечная цена на полипропиленовые емкости и резервуары из полиэтилена зависит от сложности заказа. Мы всегда выбираем самый оптимальный и взаимовыгодный вариант как для нас, так и непосредственно для заказчика. Контрольная работа №1 «Выражения и тождества» вариант 1 а-7 Контрольная работа №1 «Выражения и тождества»
«Математика», 29/02, 12, 15, 16, 18/03
А–7
|
Контрольная работа №1 «Выражения и тождества»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №1 «Выражения и тождества»
ВАРИАНТ 2
|
1. Найдите значение выражения: 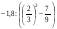 . .
2. Упростите выражение:
а) 5a – 3b – 8a + 12b;
б) 16с + (3с – 2) – (5с + 7);
в) 7 – 3(6у – 4).
3. Сравните значения выражений 0,5х – 4 и 0,6х – 3
при х = 5.
4. Упростите выражение 6,3х – 4 – 3(7,2х + 0,3) и найдите его значение при 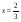 . .
5. В прямоугольном листе жести со сторонами х см и у см вырезали квадратное отверстие со стороной 5 см.
а) Найдите площадь оставшейся части.
б) Решите задачу при х = 13, у = 22.
|
1. Найдите значение выражения: 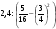 . .
2. Упростите выражение:
а) 3х + 7у – 6х – 4у;
б) 8а + (5 – а) – (7 + 11а);
в) 4 – 5(3с + 8).
3. Сравните значения выражений 3 – 0,2а и 5 – 0,3а
при а = 16.
4. Упростите выражение 3,2а – 7 – 7(2,1а – 0,3) и найдите его значение при 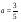 . .
5. В кинотеатре п рядов по т мест в каждом. На дневной сеанс были проданы билеты на первые 7 рядов.
а) Сколько незаполненных мест было во время сеанса?
б) Решите задачу при п = 21, т = 35.
|
А–7
|
Контрольная работа №1 «Выражения и тождества»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №1 «Выражения и тождества»
ВАРИАНТ 4
|
1. Найдите значение выражения: 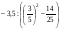 . .
2. Упростите выражение:
а) 8c – 2d – 11c + 7d;
б) 12b + (7b – 3) – (8b + 6);
в) 3 – 4(5a – 6).
3. Сравните значения выражений –3 + 0,4х и –4 + 0,5х
при х = 7.
4. Упростите выражение 3,1у – 3 – 4(6,2у + 0,2) и найдите его значение при 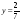 . .
5. Катя купила а ручек по 3 руб. и 15 карандашей по b руб.
а) Сколько стоит Катина покупка?
б) Решите задачу при а = 4, b = 2,5.
|
1. Найдите значение выражения: 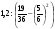 . .
2. Упростите выражение:
а) 6p + 8q – 9p – 3q;
б) 7у + (4 – 2у) – (12 + 9у);
в) 2 – 6(7х + 3).
3. Сравните значения выражений 7 – 0,6с и 8 – 0,7с
при с = 12.
4. Упростите выражение 5,3b – 6 – 5(3,7b – 0,7) и найдите его значение при 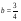 . .
5. Мама купила х кг картофеля по 6 руб. за кг и 3 кг капусты по у руб. за кг.
а) На сколько больше заплатила мама за картофель, чем за капусту?
б) Решите задачу при х = 7, у = 8,5.
|
А–7
|
Контрольная работа №2 «Уравнение с одной переменной»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №2 «Уравнение с одной переменной»
ВАРИАНТ 2
|
1. Решите уравнение:
а) 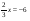 ; ;
б) 11,2 – 4х = 0;
в) 1,6(5х – 1) = 1,8х – 4,7.
2. При каком значении переменной значение выражения 3 – 2с на 4 меньше значения выражения 5с + 1?
3. Турист проехал в 7 раз большее расстояние, чем прошёл пешком. Весь путь туриста составил 24 км. Какое расстояние турист проехал?
4. Длина прямоугольника на 6 см больше ширины. Найдите площадь прямоугольника, если его периметр равен 48 см.
|
1. Решите уравнение:
а) 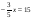 ; ;
б) 9х + 72,9 = 0;
в) 2(0,6х + 1,85) – 0,7 = 1,3х.
2. При каком значении переменной значение выражения 4а + 8 на 3 больше значения выражения 3 – 2а?
3. На одной полке на 15 книг больше, чем на другой. Всего на полках 53 книги. Сколько книг на каждой полке?
4. Ширина прямоугольника в 2 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 120 м.
|
А–7
|
Контрольная работа №2 «Уравнение с одной переменной»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №2 «Уравнение с одной переменной»
ВАРИАНТ 4
|
1. Решите уравнение:
а) 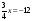 ; ;
б) 15,6 – 6х = 0;
в) 2,3(4х – 3) = 6х – 8,5.
2. При каком значении переменной b значение выражения 7 – 5b на 3 меньше значения выражения 6b + 4?
3. Мастер изготовил в 6 раз больше деталей, чем его ученик. Сколько деталей изготовил каждый из них, если вместе они изготовили 42 детали?
4. Длина прямоугольника на 3 м больше ширины. Найдите площадь прямоугольника, если его периметр равен 54 м.
|
1. Решите уравнение:
а) 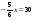 ; ;
б) 7х + 43,4 = 0;
в) 3(0,8х + 1,7) – 3,1 = 2,6х.
2. При каком значении переменной у значение выражения 3у + 9 на 8 больше значения выражения 7 – 4у?
3. В одном бидоне на 8 л больше молока, чем в другом. Всего в двух бидонах 22 л. Сколько литров молока в каждом бидоне?
4. Ширина прямоугольника в 3 раза меньше длины. Найдите площадь прямоугольника, если его периметр равен 56 м.
|
А–7
|
Контрольная работа №3 «Линейная функция»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №3 «Линейная функция»
ВАРИАНТ 2
|
1. Функция задана формулой у = х – 7. Найдите:
а) значение функции, соответствующее значению аргумента, равному 4;
б) значение аргумента, при котором значение функции равно –8.
2. а) Постройте график функции у = 3х – 4.
б) С помощью графика найдите значение функции, соответствующее значению аргумента 2,5.
3. В одной системе координат постройте графики функций:
а) у = –0,5х; б) у = 2.
4. Проходит ли график функции у = –5х + 11 через точку:
а) М(6; –41); б) N(–5; 36) ?
5. Каково взаимное расположение графиков функций
у = 15х – 51 и у = –15х + 39? В случае пересечения графиков найдите координаты точки их пересечения.
|
1. Функция задана формулой у = 5 – х. Найдите:
а) значение функции, соответствующее значению аргумента, равному 6;
б) значение аргумента, при котором значение функции равно –1.
2. а) Постройте график функции у = –2х + 5.
б) С помощью графика найдите значение функции, соответствующее значению аргумента –0,5.
3. В одной системе координат постройте графики функций:
а) у = 3х; б) у = –5.
4. Проходит ли график функции у = –7х – 3 через точку:
а) С(–8; –53); б) D(4; –25) ?
5. Каково взаимное расположение графиков функций
у = –21х – 15 и у = 21х + 69? В случае пересечения графиков найдите координаты точки их пересечения.
|
А–7
|
Контрольная работа №3 «Линейная функция»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №3 «Линейная функция»
ВАРИАНТ 4
|
1. Функция задана формулой у = х – 3. Найдите:
а) значение функции, соответствующее значению аргумента, равному 8;
б) значение аргумента, при котором значение функции равно –3.
2. а) Постройте график функции у = 5х – 3.
б) С помощью графика найдите значение функции, соответствующее значению аргумента 1,5.
3. В одной системе координат постройте графики функций:
а) у = – 1/2 х; б) у = 3.
4. Проходит ли график функции у = 6х + 13 через точку:
а) А(–8; 61); б) D (7; –55) ?
5. Каково взаимное расположение графиков функций
у = 17х – 22 и у = –17х + 46? В случае пересечения графиков найдите координаты точки их пересечения.
|
1. Функция задана формулой у = 9 – х. Найдите:
а) значение функции, соответствующее значению аргумента, равному 10;
б) значение аргумента, при котором значение функции равно –2.
2. а) Постройте график функции у = –4х + 5.
б) С помощью графика найдите значение функции, соответствующее значению аргумента –1,5.
3. В одной системе координат постройте графики функций:
а) у = 1/4 х; б) у = –2.
4. Проходит ли график функции у = –8х – 5 через точку:
а) В(6; 43); б) Р(–9; 67) ?
5. Каково взаимное расположение графиков функций
у = –27х – 33 и у = 27х + 75? В случае пересечения графиков найдите координаты точки их пересечения.
|
А–7
|
Контрольная работа №4 «Степень с натуральным показателем»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №4 «Степень с натуральным показателем»
ВАРИАНТ 2
|
1. Выполните действия:
а) х5 × х11; б) х15 : х3; в) (х4)7; г) (3х6)3.
2. Упростите выражение:
а) 4b2с × (–2,5bс4); б) (–2x10у6)4.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному –1,5;
б) значения аргумента, при которых значение функции равно 3.
4. Найдите значение выражения:
а) ; б) 3х3 – 1 при х = – .
5. Упростите выражение 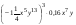 . .
|
1. Выполните действия:
а) а9 × а13; б) а18 : а6; в) (а7)4; г) (2а3)5.
2. Упростите выражение:
а) –7х5у3 × 1,5ху; б) (–3т4п13)3.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному 2,5;
б) значения аргумента, при которых значение функции равно 5.
4. Найдите значение выражения:
а) ; б) 2 – 7х2 при х = – .
5. Упростите выражение 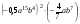 . .
|
А–7
|
Контрольная работа №4 «Степень с натуральным показателем»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №4 «Степень с натуральным показателем»
ВАРИАНТ 4
|
1. Выполните действия:
а) b8 × b15; б) b12 : b4; в) (b6)5; г) (3b8)2.
2. Упростите выражение:
а) 3x3y2 × (–3,5xy6); б) (–2a7b11)5.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному 1,5;
б) значения аргумента, при которых значение функции равно 2.
4. Найдите значение выражения:
а) ; б) 4х3 – 2 при х = – .
5. Упростите выражение 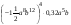 . .
|
1. Выполните действия:
а) с6 × с17; б) с20 : с5; в) (с6)3; г) (2с7)4.
2. Упростите выражение:
а) –9a7b4 × 0,5ab2; б) (–3c8d 12)4.
3. Постройте график функции у = х2. С его помощью определите:
а) значение функции, при значении аргумента, равному –2,5;
б) значения аргумента, при которых значение функции равно 6.
4. Найдите значение выражения:
а) ; б) 5 – 6х2 при х = – .
5. Упростите выражение 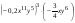 . .
|
А–7
|
Контрольная работа №5 «Сложение и вычитание многочленов»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №5 «Сложение и вычитание многочленов»
ВАРИАНТ 2
|
1. Упростите выражение:
а) (7х2 – 5х + 3) – (5х2 – 4); б) 5а2 (2а – а4).
2. Решите уравнение 30 + 5(3х – 1) = 35х – 15.
3. Вынесите общий множитель за скобки:
а) 7ха – 7хb; б) 16ху2 + 12х2у.
4. По плану тракторная бригада должна была вспахать поле за 14 дней. Бригада вспахивала ежедневно на 5 га больше, чем намечалось по плану, и потому закончила пахоту за 12 дней. Сколько гектаров было вспахано?
5. Решите уравнение:
а) 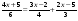 ; б) х2 + х = 0. ; б) х2 + х = 0.
|
1. Упростите выражение:
а) (3у2 – 3у + 1) – (4у – 2); б) 4b3(3b2 + b).
2. Решите уравнение 10х – 5 = 2(8х + 3) – 5х.
3. Вынесите общий множитель за скобки:
а) 8аb + 4а; б) 18ab3 – 9a2b.
4. Заказ по выпуску машин должен быть выполнен по плану за 20 дней. Но завод выпускал ежедневно по 2 машины сверх плана и поэтому выполнил заказ за 18 дней. Сколько машин должен был выпускать завод ежедневно по плану?
5. Решите уравнение:
а) 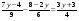 ; б) 2х2 – х = 0. ; б) 2х2 – х = 0.
|
А–7
|
Контрольная работа №5 «Сложение и вычитание многочленов»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №5 «Сложение и вычитание многочленов»
ВАРИАНТ 4
|
1. Упростите выражение:
а) (6a2 – 3a + 8) – (2a2 – 5); б) 3x4 (7x – x5).
2. Решите уравнение 14 + 4(5х – 2) = 44х – 30.
3. Вынесите общий множитель за скобки:
а) 5хy – 15y; б) 21a3b2 – 14ab3.
4. Рабочий должен был изготавливать 3 детали в час, чтобы выполнить задание вовремя. Однако он изготавливал на 1 деталь в час больше и уже за 4 ч до срока выполнил работу. Сколько деталей должен был сделать рабочий?
5. Решите уравнение:
а) 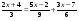 ; б) у2 + у = 0. ; б) у2 + у = 0.
|
1. Упростите выражение:
а) (4b2 – 2b + 3) – (6b – 7); б) 6y5(4y3 + y).
2. Решите уравнение 7х – 12 = 3(9х + 8) – 2х.
3. Вынесите общий множитель за скобки:
а) 6cb – 4с; б) 24x2y – 32x3y2.
4. Рабочий должен был выполнить заказ по изготовлению деталей за 12 ч. Но он выпускал на 3 детали в час больше, чем намечалось, и поэтому выполнил заказ за 10 ч. Сколько деталей должен был изготовить рабочий?
5. Решите уравнение:
а) 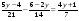 ; б) 3у2 – у = 0. ; б) 3у2 – у = 0.
|
А–7
|
Контрольная работа №6 «Умножение многочленов»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №6 «Умножение многочленов»
ВАРИАНТ 2
|
1. Представьте в виде многочлена:
а) (у – 4)(у + 5); в) (х – 3)(х2 + 2х – 6).
б) (3а + 2b)(5а – b);
2. Разложите на множители:
а) b(b + 1) – 3(b + 1); б) ca – cb + 2a – 2b.
3. Упростите выражение (а2 – b2)(2a + b) – аb(а + b).
4. Докажите тождество (х – 3)(х + 4) = х(х + 1) – 12.
5. Ширина прямоугольника вдвое меньше его длины. Если ширину увеличить на 3 см, а длину на 2 см, то площадь его увеличится на 78 см2. Найдите длину и ширину прямоугольника.
|
1. Представьте в виде многочлена:
а) (х + 7)(х – 2); в) (y + 5)(y2 – 3у + 8).
б) (4с – d)(6c + 3d);
2. Разложите на множители:
а) у(а – b) + 2(а – b); б) 3х – 3у + ах – ау.
3. Упростите выражение ху(х + у) – (х2 + у2)(х – 2у).
4. Докажите тождество а(а – 2) – 8 = (а + 2)(а – 4).
5. Длина прямоугольника на 12 дм больше его ширины. Если длину увеличить на 3 дм, а ширину – на 2 дм, то площадь его увеличится на 80 дм2. Найдите длину и ширину прямоугольника.
|
А–7
|
Контрольная работа №6 «Умножение многочленов»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №6 «Умножение многочленов»
ВАРИАНТ 4
|
1. Представьте в виде многочлена:
а) (а – 3)(а + 6); в) (b – 2)(b2 + 3b – 8).
б) (5х – у)(6х + 4у);
2. Разложите на множители:
а) c(d – 5) + 6(d – 5); б) bx – by + 4x – 4y.
3. Упростите выражение (c2 + d 2)(c + 3d) – cd(3c – d).
4. Докажите тождество (y – 5)(y + 7) = y(y + 2) – 35.
5. Ширина прямоугольника на 6 см меньше его длины. Если ширину увеличить на 5 см, а длину на 2 см, то площадь его увеличится на 110 см2. Найдите длину и ширину прямоугольника.
|
1. Представьте в виде многочлена:
а) (b + 8)(b – 3); в) (a + 4)(a2 – 6a + 2).
б) (6p – q)(3p + 5q);
2. Разложите на множители:
а) a(x + y) – 5(x + y); б) 5a – 5b + da – db.
3. Упростите выражение mn(m – n) – (m2 – n2)(2m + n).
4. Докажите тождество b(b – 3) – 18 = (b + 3)(b – 6).
5. Длина прямоугольника в 3 раза больше его ширины. Если длину увеличить на 2 м, а ширину – на 3 м, то площадь его увеличится на 72 м2. Найдите длину и ширину прямоугольника.
|
А–7
|
Контрольная работа №7 «Формулы сокращенного умножения»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №7 «Формулы сокращенного умножения»
ВАРИАНТ 2
|
1. Преобразуйте в многочлен:
а) (а – 3)2; в) (4а – b)(4а + b);
б) (2у + 5)2; г) (х2 + 1)(х2 – 1).
2. Разложите на множители:
а) с2 – 0,25; б) х2 – 8х + 16.
3. Найдите значение выражения (х + 4)2 – (х – 2)(х + 2)
при х = 0,125.
4. Выполните действия:
а) 2(3х – 2у)(3х + 2у); в) (а – 5)2 – (а + 5)2.
б) (а 3 + b 2) 2;
5. Решите уравнение:
а) (2х – 5)2 – (2х – 3)(2х + 3) = 0; б) 9у2 – 25 = 0.
|
1. Преобразуйте в многочлен:
а) (х + 4)2; в) (2у + 5)(2у – 5);
б) (3b – с)2; г) (у 2 – х)(у 2 + х).
2. Разложите на множители:
а) – а2; б) b2 + 10b + 25.
3. Найдите значение выражения (а – 2b)2 + 4b(а – b) при а = – .
4. Выполните действия:
а) 3(1 + 2ху)(1 – 2ху); в) (а + b)2 – (а – b)2.
б) (х 2 – у 3) 2;
5. Решите уравнение:
а) (4х – 3)(4х + 3) – (4x – 1)2 = 3x; б) 16с2 – 49 = 0.
|
А–7
|
Контрольная работа №7 «Формулы сокращенного умножения»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №7 «Формулы сокращенного умножения»
ВАРИАНТ 4
|
1. Преобразуйте в многочлен:
а) (b – 5)2; в) (6x – y)(6x + y);
б) (4a + c)2; г) (p 2 + q)(p 2 – q).
2. Разложите на множители:
а) x2 – 0,81; б) a 2 – 6a + 9.
3. Найдите значение выражения (y + 5)2 – (y – 5)(y + 5)
при y = –4,7.
4. Выполните действия:
а) 4(5a – b)(5a + b); в) (x + 6)2 – (x – 6)2.
б) (c 4 + d 3) 2;
5. Решите уравнение:
а) (3х – 2)2 – (3х – 1)(3х + 1) = –2x; б) 25a2 – 81 = 0.
|
1. Преобразуйте в многочлен:
а) (c + 7)2; в) (3x – 4)(3x + 4);
б) (5c – 2)2; г) (a 2 + 2)(a 2 – 2).
2. Разложите на множители:
а) – b 2; б) y 2 + 12y + 36.
3. Найдите значение выражения (3x – y)2 – 3x(3x – 2y) при y = – .
4. Выполните действия:
а) 5(3mn + 1)(3mn – 1); в) (c – d)2 – (c + d)2.
б) (a 3 – b 4) 2;
5. Решите уравнение:
а) (5х – 1)(5х + 1) – (5x + 2)2 = 0; б) 36b2 – 121 = 0.
|
А–7
|
Контрольная работа «Преобразования целых выражений»
ВАРИАНТ 1
|
А–7
|
Контрольная работа «Преобразования целых выражений»
ВАРИАНТ 2
|
1. Преобразуйте в многочлен:
а) (а – 2)(а + 2) – 2а(5 – а); в) 3(х – 4)2 – 3х2.
б) (у – 9)2 – 3у(у + 1);
2. Разложите на множители:
а) 25х – х3; б) 2х2 – 20х + 50.
3. Упростите выражение (с2 – b)2 – (с2 – 1)(с2 + 1) + 2bс2 и найдите его значение при b = – 3.
4. Представьте в виде произведения:
а) (х – 4)2 – 25х2; б) а2 – b2 – 4b – 4а.
5. Докажите тождество (а + b)2 – (а – b)2 = 4аb.
|
1. Преобразуйте в многочлен:
а) 4х(2х – 1) – (х – 3)(х + 3); в) 7(а + b)2 – 14аb.
б) (р + 3)(р – 11) + (р + 6)2;
2. Разложите на множители:
а) у3 – 49у; б) –3а2 – 6ab – 3b2.
3. Упростите выражение (а – l)2(a + 1) + (а + 1)(а – 1) и найдите его значение при а = – 3.
4. Представьте в виде произведения:
а) (у – 6)2 – 9у2; б) с2 – d 2 – с + d.
5. Докажите тождество (х – у)2 + (х + у)2 = 2(х 2 + у 2).
|
А–7
|
Контрольная работа «Преобразования целых выражений»
ВАРИАНТ 3
|
А–7
|
Контрольная работа «Преобразования целых выражений»
ВАРИАНТ 4
|
1. Преобразуйте в многочлен:
а) (b – 3)(b + 3) – 3b(4 – b); в) 5(y – 3)2 – 5y 2.
б) (c – 6)2 – 4c(2c + 5);
2. Разложите на множители:
а) 81a – a3; б) 6b2 – 36b + 54.
3. Упростите выражение (x + y2)2 – (y2 – 2)(y2 + 2) – 2xy2 и найдите его значение при x = – 5.
4. Представьте в виде произведения:
а) (х – 2)2 – 36х2; б) c2 – d 2 – 7d – 7c.
5. Докажите тождество b4 – 1 = (b – 1)(b3 + b2 + b + 1).
|
1. Преобразуйте в многочлен:
а) 5y(3y – 2) – (y – 1)(y + 1); в) 6(c + d)2 – 12cd.
б) (d – 8)(d + 4) + (d – 5)2;
2. Разложите на множители:
а) b3 – 36b; б) –2а2 + 8ab – 8b2.
3. Упростите выражение (b + 3)2(b – 3) + 3(b + 3)(b – 3) и найдите его значение при b = – 2.
4. Представьте в виде произведения:
а) (у – 3)2 – 16у2; б) x2 – y2 – y – x.
5. Докажите тождество a4 – 1 = (a – 1)(a3 + a2 + a + 1).
|
А–7
|
Контрольная работа №9 «Системы линейных уравнений»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №9 «Системы линейных уравнений»
ВАРИАНТ 2
|
1. Решите систему уравнений 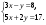
2. Студент получил стипендию 100 рублей монетами достоинством 5 рублей и 2 рубля, всего 32 монеты. Сколько было выдано монет каждого номинала?
3. Решите систему уравнений 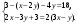
4. Постройте график уравнения 4х – 3у = 12.
5. Имеет ли решения система 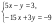 и сколько? и сколько?
|
1. Решите систему уравнений 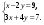
2. Кассир разменял 500-рублевую купюру на 50-рублевые и 10-рублевые, всего 22 купюры. Сколько было выдано кассиром 50-рублевых и 10-рублевых купюр?
3. Решите систему уравнений 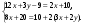
4. Постройте график уравнения 6у – 7х = 42.
5. Имеет ли решения система 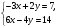 и сколько? и сколько?
|
А–7
|
Контрольная работа №9 «Системы линейных уравнений»
ВАРИАНТ 3
|
А–7
|
Контрольная работа №9 «Системы линейных уравнений»
ВАРИАНТ 4
|
1. Решите систему уравнений 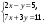
2. Купили 27 тетрадей по 2 рубля и по 5 рублей, заплатив за всю покупку 93 рубля. Сколько тетрадей каждого вида купили?
3. Решите систему уравнений 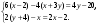
4. Постройте график уравнения 3х – 5у = 15.
5. Имеет ли решения система 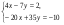 и сколько? и сколько?
|
1. Решите систему уравнений 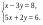
2. Купили 15 гвоздик по 3 рубля и по 4 рубля, заплатив за всю покупку 54 рубля. Сколько купили гвоздик каждого вида?
3. Решите систему уравнений 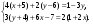
4. Постройте график уравнения 2у – 9х = 18.
5. Имеет ли решения система 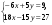 и сколько? и сколько?
|
А–7
|
Контрольная работа №10 «Итоговая»
ВАРИАНТ 1
|
А–7
|
Контрольная работа №10 «Итоговая»
ВАРИАНТ 2
|
1. Упростите выражение:
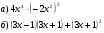
2. Разложите на множители:
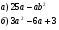
3. Решите равнение 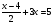 . .
4. Одно полотно разрезали на 5 равных частей, а другое, длина которого на 10 м больше, на 7 таких же частей. Какова длина каждого полотна?
5. Постройте график функции 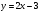 и найдите координаты точки пересечения этого графика с прямой и найдите координаты точки пересечения этого графика с прямой 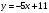 . .
|
1. Упростите выражение:
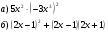
2. Разложите на множители:
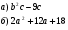
3. Решите равнение 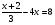 . .
Муку рассыпали в 8 одинаковых по весу пакетов, а сахар – в 6 таких же пакетов. Сколько весит мука и сколько весит сахар, если сахара было на 10 кг меньше?
5. Постройте график функции 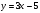 и найдите координаты точки пересечения этого графика с прямой и найдите координаты точки пересечения этого графика с прямой 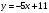 . .
| |
|
|
 Скачать 189.24 Kb.
Скачать 189.24 Kb. .
. .
.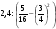 .
.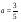 .
.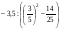 .
.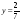 .
.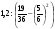 .
.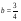 .
.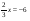 ;
;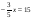 ;
;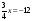 ;
;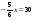 ;
;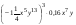 .
.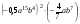 .
.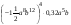 .
.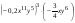 .
.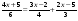 ; б) х2 + х = 0.
; б) х2 + х = 0.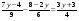 ; б) 2х2 – х = 0.
; б) 2х2 – х = 0.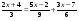 ; б) у2 + у = 0.
; б) у2 + у = 0.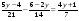 ; б) 3у2 – у = 0.
; б) 3у2 – у = 0.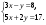
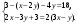
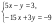 и сколько?
и сколько?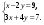
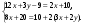
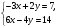 и сколько?
и сколько?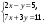
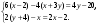
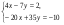 и сколько?
и сколько?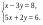
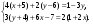
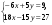 и сколько?
и сколько?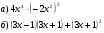
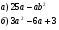
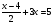 .
.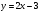 и найдите координаты точки пересечения этого графика с прямой
и найдите координаты точки пересечения этого графика с прямой 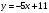 .
.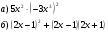
 .
.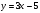 и найдите координаты точки пересечения этого графика с прямой
и найдите координаты точки пересечения этого графика с прямой