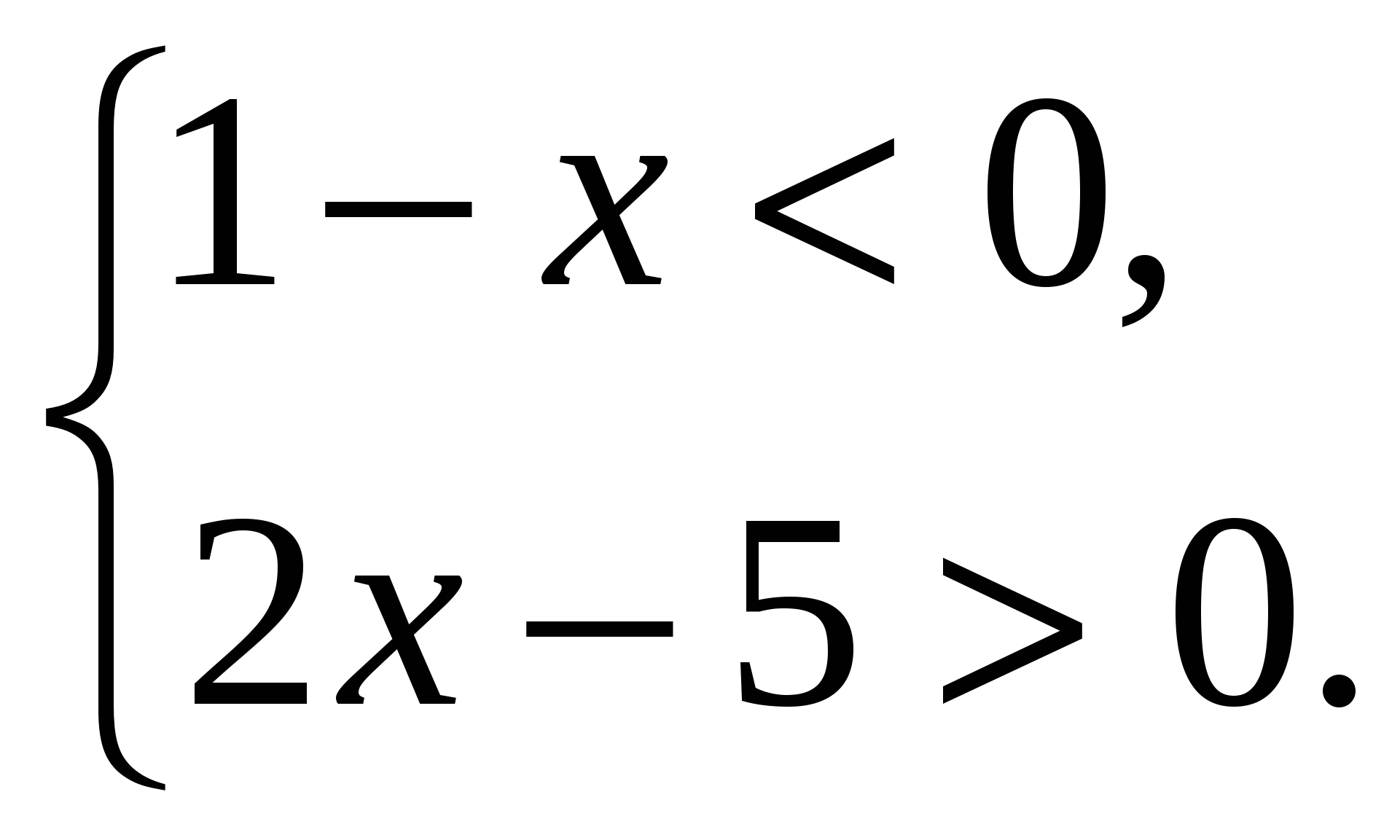|
Рабочая программа по предмету алгебра 8 класс кол-во часов 119 за год, в неделю 4ч в 1-м полугодии, 3ч во 2-м
Муниципальное бюджетное общеобразовательное учреждение
Чалтырская средняя общеобразовательная школа №1
Рассмотрено Согласовано Утверждаю
на заседании зам. дир. по УВР директор СОШ №1
ШМО учителей __________________ _________________ __________________ ___________________ Хаспекян А. Г.
Протокол № 1 « » ______________ приказ № ____от_____
от ________________
РАБОЧАЯ ПРОГРАММА
по предмету
АЛГЕБРА
8 класс
кол-во часов – 119 за год,
в неделю – 4ч. в 1-м полугодии, 3ч. – во 2-м
Килафян Аракси Хевондовна
ФИО учителя
2012/13 уч.г.
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
Нормативные документы, обеспечивающие реализацию программы.
«Об утверждении федерального компонента государственных образовательных стандартов начального общего, основного общего и среднего (полного) общего образования». Приказ Министерства образования Российской федерации от 5.03.2004г. №1089
Федеральный компонент государственного стандарта среднего (полного) общего образования по математике.// Вестник образования России, 2004, №13, стр.72-77.
«Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования». Приказ Министерства образования Российской федерации от 5.03.2004г. №1089
«Об утверждении федерального государственного образовательного стандарта основного общего образования». Приказ Министерства образования Российской федерации от 17.12.2010 года № 1897.
«Об утверждении федеральных перечней учебников, рекомендованных (допущенных) к использованию в образовательном процессе в образовательных учреждениях, реализующих образовательные программы общего образования и имеющих государственную аккредитацию, на 2012\2013 учебный год». Приказ Министерства образования Российской федерации от 27.12.2011 года № 2885.
Программы общеобразовательных учреждений. Алгебра. 7-9 классы. Составитель – Бурмистрова Т.А. – М.: Просвещение, 2009 г.
Закон «Об образовании» РФ.
Рабочая программа составлена на основе Фундаментального ядра содержания общего образования и Требований к результатам освоения основной общеобразовательной программы основного общего образования, представленных в Федеральном государственном образовательном стандарте общего образования. В ней также учитываются основные идеи и положения Программы развития и формирования универсальных учебных действий для основного общего образования.
Алгебра является одним из опорных предметов основной школы: она обеспечивает изучение других дисциплин. В первую очередь это относится к предметам естественно-научного цикла, в частности к физике. Развитие логического мышления учащихся при обучении алгебре способствует усвоению предметов гуманитарного цикла. Практические умения и навыки алгебраического характера необходимы для трудовой и профессиональной подготовки школьников.
Развитие у учащихся правильных представлений о сущности и происхождении алгебраических абстракций, соотношении реального и идеального, характере отражения математической наукой явлений и процессов реального мира, месте алгебры в системе наук и роли математического моделирования в научном познании и в практике способствует формированию научного мировоззрения учащихся и качеств мышления, необходимых для адаптации в современном информационном обществе.
Требуя от учащихся умственных и волевых усилий, концентрации внимания, активности развитого воображения, алгебра развивает нравственные черты личности (настойчивость, целеустремленность, творческую активность, самостоятельность, ответственность, трудолюбие, дисциплину и критичность мышления) и умение аргументированно отстаивать свои взгляды и убеждения, а также способность принимать самостоятельные решения.
Изучение алгебры, функций, вероятности и статистики существенно расширяет кругозор учащихся, знакомя их с индукцией и дедукцией, обобщением и конкретизацией, анализом и синтезом, классификацией и систематизацией, абстрагированием, аналогией. Активное использование задач на всех этапах учебного процесса развивает творческие способности школьников.
Изучение алгебры позволяет формировать умения и навыки умственного труда — планирование своей работы, поиск рациональных путей её выполнения, критическая оценка результатов. В процессе изучения алгебры школьники должны научиться излагать свои мысли ясно и исчерпывающе, лаконично и ёмко, приобрести навыки чёткого, аккуратного и грамотного выполнения математических записей.
Цели изучения курса.
Общеучебные:
Развить умения количественного сопоставления величин в реальной практической деятельности (грамотное использование для изучения окружающего мира таких методов, как наблюдение, моделирование измерение; оценка точности измерения и вычисления; использование МК для выполнения практических расчетов).
Развить умения определять структуру предмета или явления, распознавать связи между элементами предмета или явления, строить для них простейшие функциональные зависимости на выявленных причинно-следственных связей.
Добиться осознания необходимости использования элементов алгоритмической культуры.
Добиться осознания необходимости приобретения навыков моделирования реальных ситуаций с помощью изучаемых математических объектов, навыков исследования полученных моделей.
Продолжить формирование базы для успешного изучения других разделов математики, смежных дисциплин.
Предменто-ориентированные:
Довести умение решать неравенства первой степени и их системы до автоматизма.
Довести умение осуществлять оценку точности измерения и вычисления, использовать МК для выполнения практических расчетов до автоматизма.
Развить представления о числе. Добиться усвоения понятий иррацонального и действительного числа, расширения круга решаемых практических задач.
Добиться усвоения геометрической интерпретации действительного числа, совершенной заполненности числовой прямой, как пропедевтики понимания элементов анализа.
Научить выполнять преобразования выражений, содержащих квадратные корни.
Научить находить приближенное значение квадратного корня.
Довести умение решать квадратные уравнения и к ним сводящиеся до автоматизма.
Развить умение решать текстовые задачи с помощью квадратных уравнений.
Научить анализировать процессы, моделируемые с помощью квадратных уравнений.
Развить технику построения и чтения графиков функций.
Усвоить необходимую сумму знаний для успешного изучения других разделов математики.
Важнейшей задачей школьного курса алгебры является развитие логического мышления учащихся. Сами объекты математических умозаключений и принятые в алгебре правила их конструирования способствуют формированию умений обосновывать и доказывать суждения, приводить чёткие определения, развивают логическую интуицию, кратко и наглядно раскрывают механизм логических построений и учат их применению.
Тем самым алгебра занимает одно из ведущих мест в формировании научно-теоретического мышления школьников. Раскрывая внутреннюю гармонию математики, формируя понимание красоты и изящества математических рассуждений, алгебра вносит значительный вклад в эстетическое воспитание учащихся.
Место предмета в Базисном учебном плане
Базисный учебный (образовательный) план на изучение алгебры в 7 – 9 классах основной школы отводит 3 часа в неделю в течение каждого года обучения, всего 315 уроков. В первом полугодии 8 класса отводится 4 урока в неделю за счёт вариативной части Базисного плана, т.е. 119 уроков на весь учебный год.
Структура курса.
|
Тема + содержание
|
Примерное количество часов
|
1
|
Рациональные дроби и их свойства. Свойства рациональных дробей. Сумма и разность дробей. Произведение и частное дробей.
|
22
|
2
|
Квадратные корни. Действительные числа. Арифметический квадратный корень и его свойства. Применение свойств арифметического квадратного корня.
|
23
|
3
|
Квадратные уравнения. Квадратное уравнение и его корни. Дробные рациональные уравнения. Решение текстовых задач с помощью рациональных уравнений.
|
24
|
4
|
Неравенства. Числовые неравенства и их свойства. Неравенства с одной переменной и их системы.
|
19
|
5
|
Степень с целым показателем. Степень с целым показателем и её свойства. Стандартный вид числа.
|
9
|
6
|
Элементы статистики. Сбор и группировка статистических данных. Наглядное представление ста-тистической информации.
|
7
|
|
Итого по модулям
|
104
|
|
Вводное и итоговое повторение
|
15
|
|
Общее количество часов
|
119
|
ТРЕБОВАНИЯ К РЕЗУЛЬТАТАМ ОБУЧЕНИЯ
И ОСВОЕНИЮ СОДЕРЖАНИЯ КУРСА
Программа обеспечивает достижение следующих результатов освоения образовательной программы основного общего образования:
личностные:
сформированность ответственного отношения к учению, готовность и способности обучающихся к саморазвитию и самообразованию на основе мотивации к обучению и познанию, выбору дальнейшего образования на базе ориентировки в мире профессий и профессиональных предпочтений, осознанному построению индивидуальной образовательной траектории с учётом устойчивых познавательных интересов;
сформированность целостного мировоззрения, соответствующего современному уровню развития науки и общественной практики;
сформированность коммуникативной компетентности в общении и сотрудничестве со сверстниками, старшими и младшими, в образовательной, общественно полезной, учебно-исследовательской, творческой и других видах деятельности;
умение ясно, точно, грамотно излагать свои мысли в устной и письменной речи, понимать смысл поставленной задачи, выстраивать аргументацию, приводить примеры и контрпримеры;
представление о математической науке как сфере человеческой деятельности, об этапах её развития, о её значимости для развития цивилизации;
критичность мышления, умение распознавать логически некорректные высказывания, отличать гипотезу от факта;
креативность мышления, инициатива, находчивость, активность при решении алгебраических задач;
умение контролировать процесс и результат учебной математической деятельности;
способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений.
метапредметные:
умение самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных и познавательных задач;
умение осуществлять контроль по результату и по способу действия на уровне произвольного внимания и вносить необходимые коррективы;
умение адекватно оценивать правильность или ошибочность выполнения учебной задачи, её объективную трудность и собственные возможности её решения;
осознанное владение логическими действиями определения понятий, обобщения, установления аналогий, классификации на основе самостоятельного выбора оснований и критериев, установления родовидовых связей;
умение устанавливать причинно-следственные связи; строить логическое рассуждение, умозаключение (индуктивное, дедуктивное и по аналогии) и выводы;
умение создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных и познавательных задач;
умение организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками: определять цели, распределение функций и ролей участников, взаимодействие и общие способы работы; умение работать в
группе: находить общее решение и разрешать конфликты на основе согласования позиций и учёта интересов; слушать партнёра; формулировать, аргументировать и отстаивать своё мнение;
сформированность учебной и общепользовательской компетентности в области использования информационно-коммуникационных технологий (ИКТ-компетентности);
первоначальные представления об идеях и о методах математики как об универсальном языке науки и техники, о средстве моделирования явлений и процессов;
умение видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни;
умение находить в различных источниках информацию, необходимую для решения математических проблем, и представлять её в понятной форме; принимать решение в условиях неполной и избыточной, точной и вероятностной информации;
умение понимать и использовать математические средства наглядности (рисунки, чертежи, схемы и др.) для иллюстрации, интерпретации, аргументации;
умение выдвигать гипотезы при решении учебных задач и понимать необходимость их проверки;
умение применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач;
понимание сущности алгоритмических предписаний и умение действовать в соответствии с предложенным алгоритмом;
умение самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических проблем;
умение планировать и осуществлять деятельность, направленную на решение задач исследовательского характера.
предметные:
умение работать с математическим текстом (структурирование, извлечение необходимой информации), точно и грамотно выражать свои мысли в устной и письменной речи, применяя математическую терминологию и символику, использовать различные языки математики (словесный, символический, графический), обосновывать суждения, проводить классификацию, доказывать математические утверждения;
владение базовым понятийным аппаратом: иметь представление о числе, владение символьным языком алгебры, знание элементарных функциональных зависимостей, формирование представлений о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
умение выполнять алгебраические преобразования рациональных выражений, применять их для решения учебных математических задач и задач, возникающих в смежных учебных предметах;
умение пользоваться математическими формулами и самостоятельно составлять формулы зависимостей между величинами на основе обобщения частных случаев и эксперимента;
умение решать линейные и квадратные уравнения и неравенства, а также приводимые к ним уравнения, неравенства, системы; применять графические представления для решения и исследования уравнений, неравенств, систем;
применять полученные умения для решения задач из математики, смежных предметов, практики;
овладение системой функциональных понятий, функциональным языком и символикой, умение строить графики функций, описывать их свойства, использовать функционально-графические представления для описания и анализа математических задач и реальных зависимостей;
овладение основными способами представления и анализа статистических данных; умение решать задачи на нахождение частоты и вероятности случайных событий;
умение применять изученные понятия, результаты и методы при решении задач из различных разделов курса, в том числе задач, не сводящихся к непосредственному применению известных алгоритмов.
В результате изучения алгебры в 8 классе ученик должен
существо понятия математического доказательства; примеры доказательств;
существо понятия алгоритма; примеры алгоритмов;
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
как потребности практики привели математическую науку к необходимости расширения понятия числа;
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации;
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
решать линейные неравенства с одной переменной и их системы;
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
описывать свойства изученных функций, строить их графики;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами; нахождения нужной формулы в справочных материалах;
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
описания зависимостей между физическими величинами соответствующими формулами при исследовании несложных практических ситуаций;
интерпретации графиков реальных зависимостей между величинами.
Контроль реализации программы.
Стартовый контроль.
Вариант 1
Как записать на языке математики предложение: «Утроенная разность кубов чисел k и v» ?
а) (3k)3 – (3v)3 ; б) 3(k – v)3 ; в) 3(k3 – v3); г) (3k – 3v)3.
Составить математическую модель ситуации: «Карандаш стоит х рублей. Ручка стоит у рублей. Пять карандашей стоят столько же, сколько три ручки»
а) 5х+3у=0; б) х+у=3+5; в) 5х=3у; г) 3х=5у.
3. Вычислить (-1)6-16.
а) 0; б) 2; в) -1; г) -2.
4. Упростить: с12: с4.
а) с3; б) с16; в) с8; г) с48.
5. Упростить: р8· р2.
а) р10; б) р16; в) р4; г) р6.
6. Упростить: (3 р3с)3.
а) 3р9с3; б) 9р9с3; в) 9р6с3; г) 27р9с3.
7. Привести подобные члены 7а – 5х + 3а + 4х – х + 2у.
а) 10а – 2х + 2у; б) 10аху; в) 10а – 10х + 2у; г) 10а + 10х +2у.
8. Упростить выражение: 3а – (2а – 3х) + (4а – 2х) – (х + 5а).
а) 0; б) 10а – 6х; в) 10а; г) – 6х.
9. Решить уравнение 3(2х – 1) – 2(3 – 7х) = 2(5х – 2).
а) 2; б) 0,5; в) 
10. Привести многочлен к стандартному виду (2а – 3)(а + 5).
11. Раскрыть скобки (3а – 2)2.
12. Разложить на множители х2 – 16.
13. Разложить на множители а2 + 16а + 64.
14. Разложить на множители 18а3р + 24ар2 – 6ар.
15. Разложить на множители 3а + 3с + ха + сх.
16. Определить, проходит ли график функции у = - 2х + 3 через точку
Р( -1; 5).
Построить график функции у = 1 – х.
Решить систему уравнений 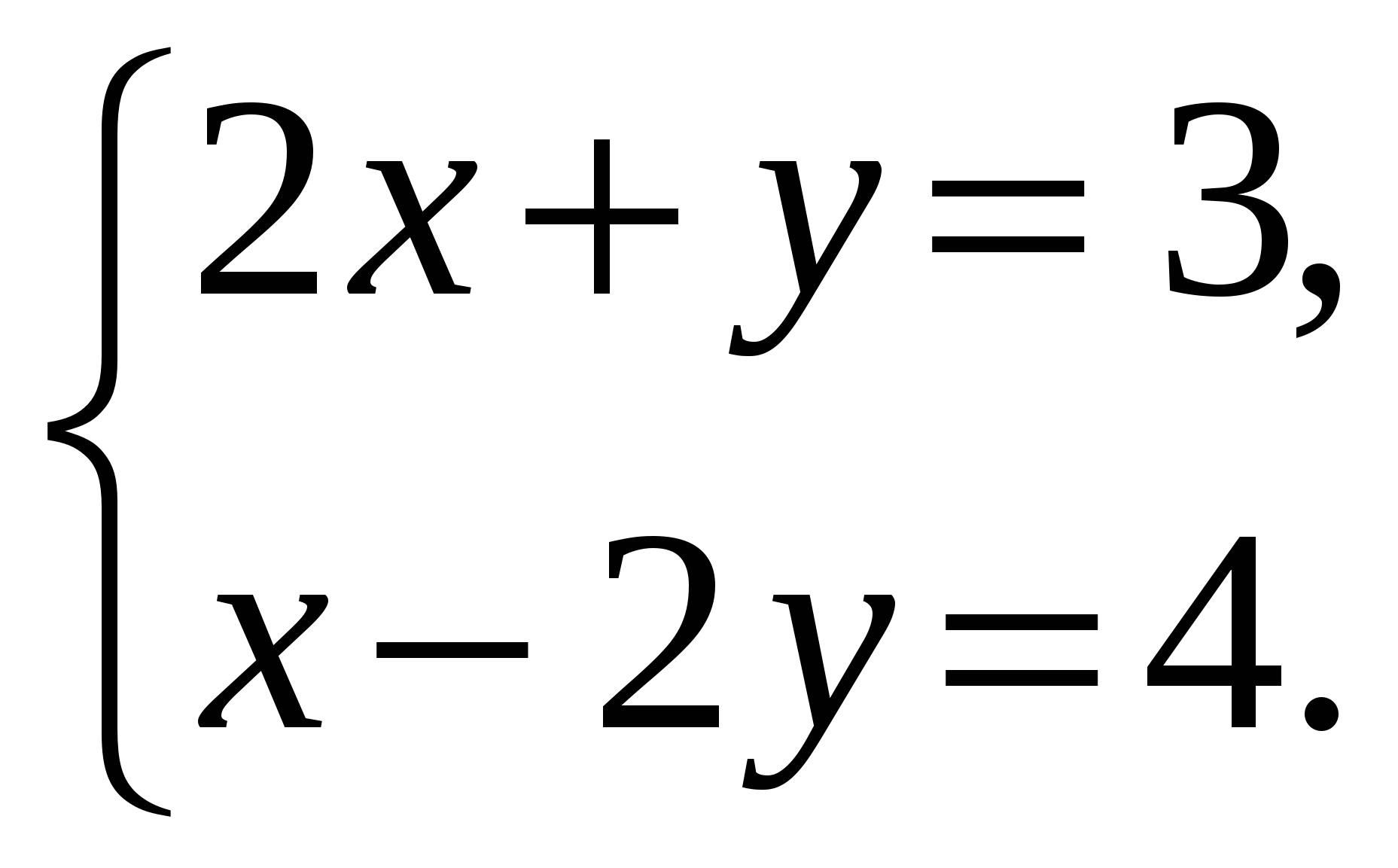
Вариант 2
Как записать на языке математики предложение: «Удвоенная сумма кубов чисел k и v» ?
а) (2k)3 – (2v)3 ; б) 2(k + v)3 ; в) 2(k3 + v3); г) (2k + 2v)3.
Составить математическую модель ситуации: «Купили х кг яблок по у рублей за 1 кг и 5 кг груш по а рублей за кг. Стоимость купленных яблок равна стоимости купленных груш»
а) ху + 5а=0; б) х+у=а+5; в) 5х=ау; г) ху=5а.
Вычислить (-1)16-116.
а) 0; б) 2; в) -1; г) -2.
Упростить: с18: с6.
а) с3; б) с12; в) с24; г) с108.
Упростить: р12· р2.
а) р14; б) р10; в) р24; г) р6.
Упростить: (4 р3с)3.
а) 4р9с3; б) 16р9с3; в) 16р6с3; г) 64р9с3.
Привести подобные члены 17а – 5х + 3а + 4х – х + 5у.
а) 20а – 2х + 5у; б) 23аху; в) 20а – 10х + 5у; г) 20а + 10х +5у.
Упростить выражение: 3у – (2у – 3х) + (4у – 2х) – (х + 5у).
а) 0; б) 10у – 6х; в) 10у; г) – 6х.
Решить уравнение 3(2х – 1) – 2(5х - 2) = 2(3 – 7х).
а) 2; б) 0,5; в) 
Привести многочлен к стандартному виду (3а – 2)(а + 5).
11. Раскрыть скобки (5а – 2)2.
12. Разложить на множители х2 – 9.
13. Разложить на множители а2 + 10а + 25.
14. Разложить на множители 36а3р + 42ар2 – 6ар.
15. Разложить на множители 7а + 7с + ха + сх.
16. Определить, проходит ли график функции у = - 2х + 3 через точку
С( 1; 1).
Построить график функции у = 1+ х.
Решить систему уравнений 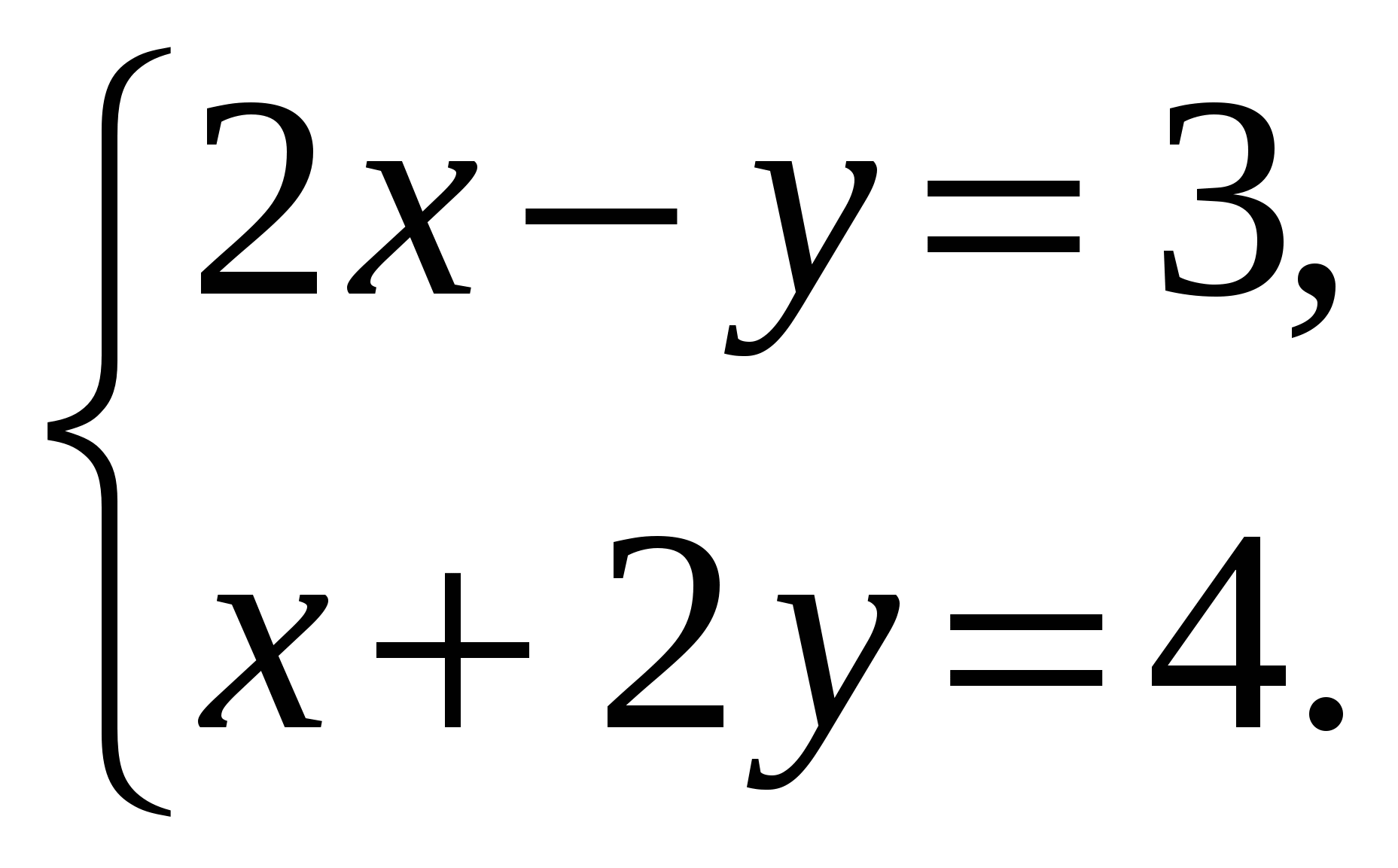
Комплект теоретических вопросов на конец года
Приведите примеры целых и дробных выражений.
Какую дробь называют рациональной? Приведите пример.
Дайте определение тождества. Приведите пример.
Сформулируйте основное свойство дроби.
Сформулируйте правило об изменении знака перед дробью.
Сформулируйте правило сложения (вычитания) дробей с одинаковыми знаменателями.
Как выполняют сложение (вычитание дробей с разными знаменателями)?
Сформулируйте правило умножения дробей.
Сформулируйте правило возведения дроби в степень.
Сформулируйте правило деления дробей.
Какая функция называется обратной пропорциональностью?
В каких координатных четвертях расположен график функции 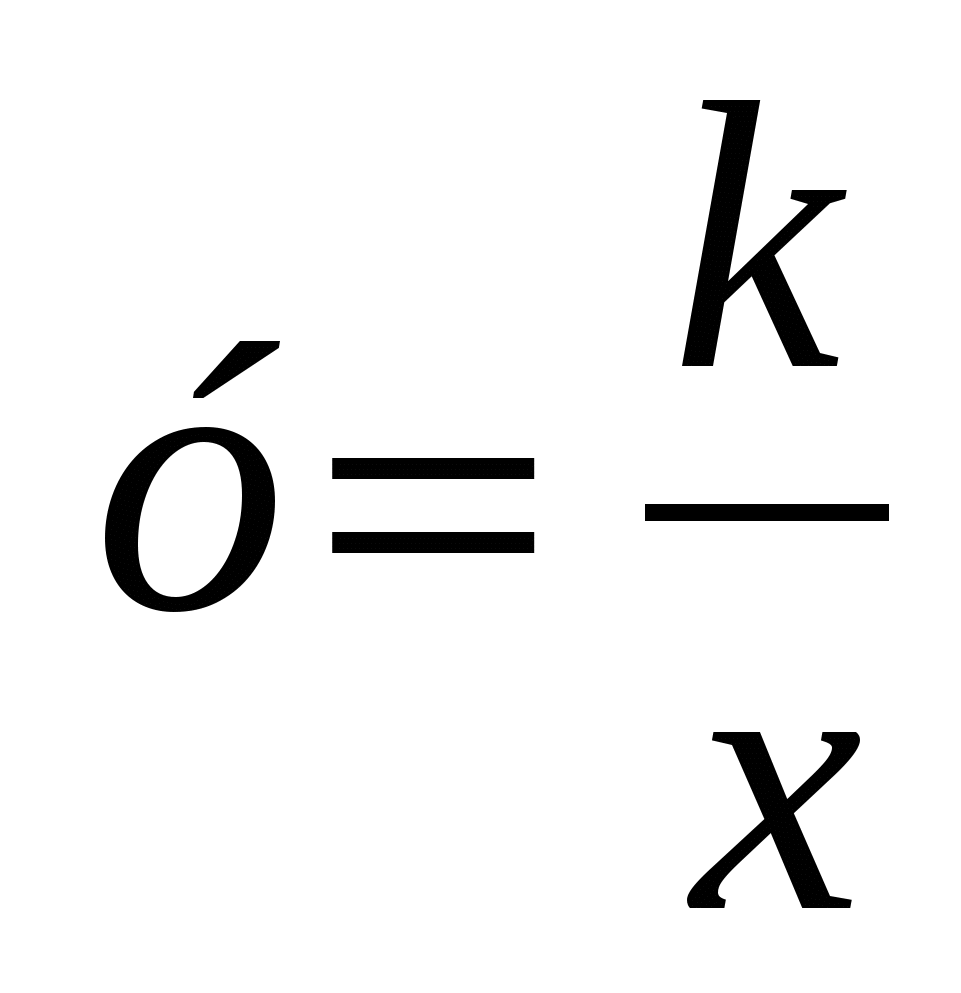 при при 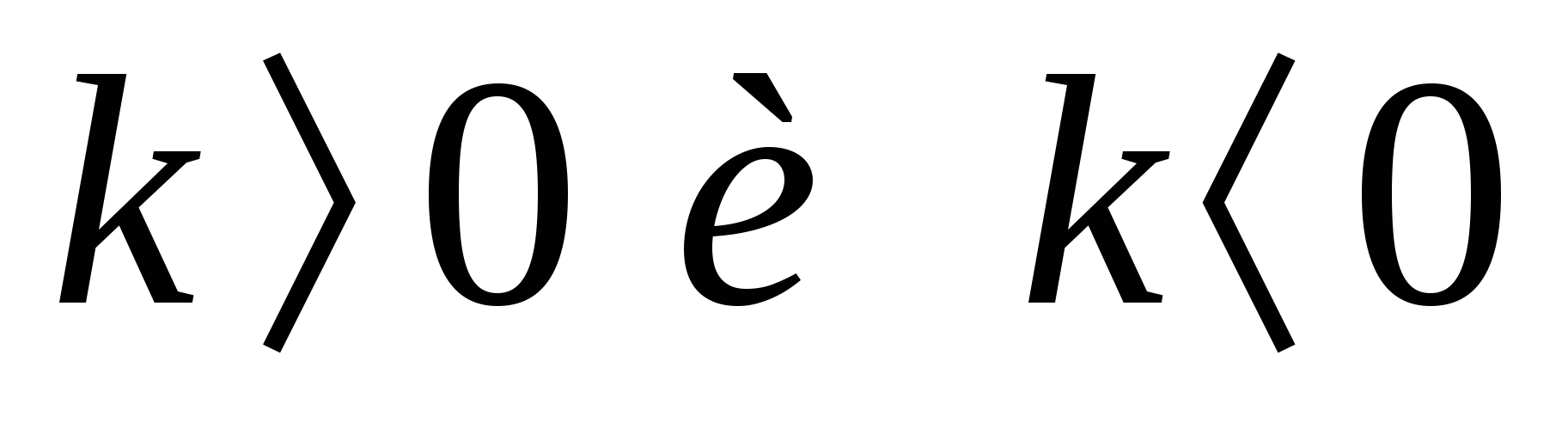 ? ?
Какие числа образуют множество действительных чисел?
Какие действительные числа можно и какие нельзя представить в виде отношения целого числа к натуральному?
Приведите пример бесконечной десятичной дроби, которая является: а) рациональным числом; б) иррациональным числом.
Сформулируйте определение арифметического квадратного корня. При каких значениях а выражение 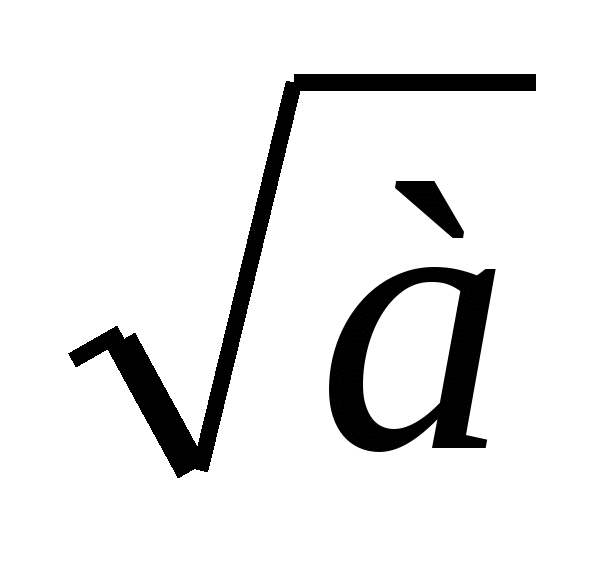 имеет смысл? имеет смысл?
Имеет ли уравнение х2 = а корни при 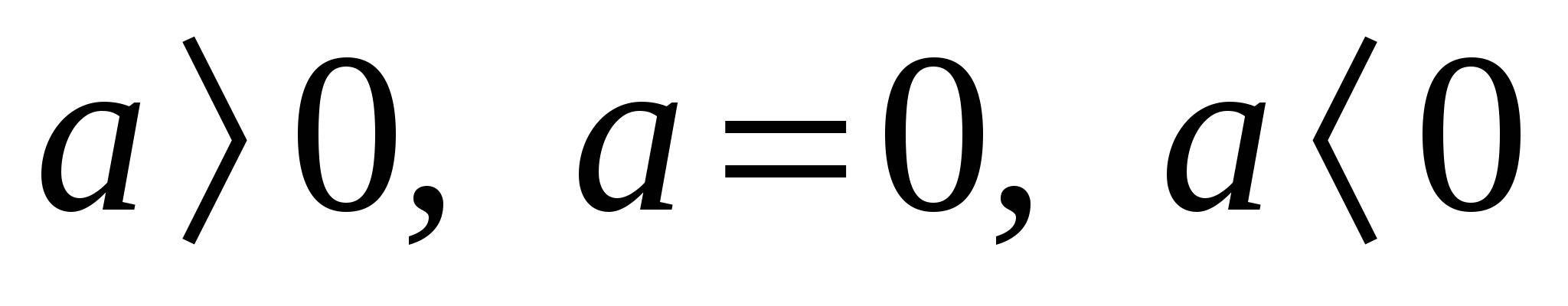 и если имеет, то сколько? и если имеет, то сколько?
Какова область определения функции 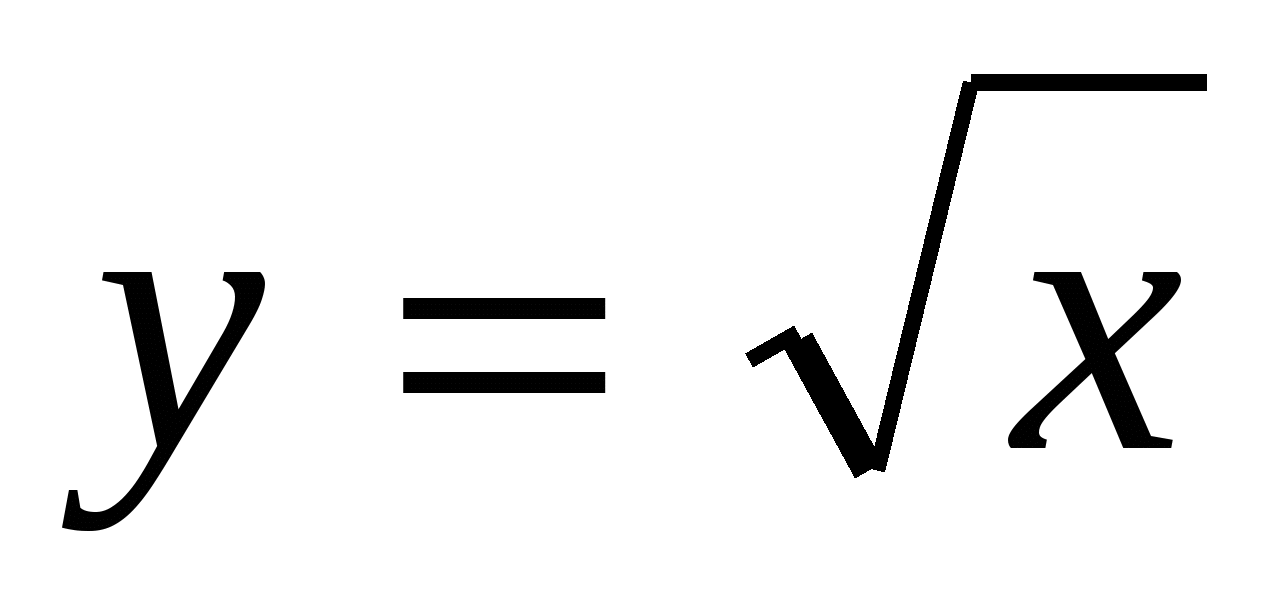 ? Как расположен график этой функции в координатной плоскости? ? Как расположен график этой функции в координатной плоскости?
Сформулируйте теорему о квадратном корне из произведения (дроби).
Продолжите тождество 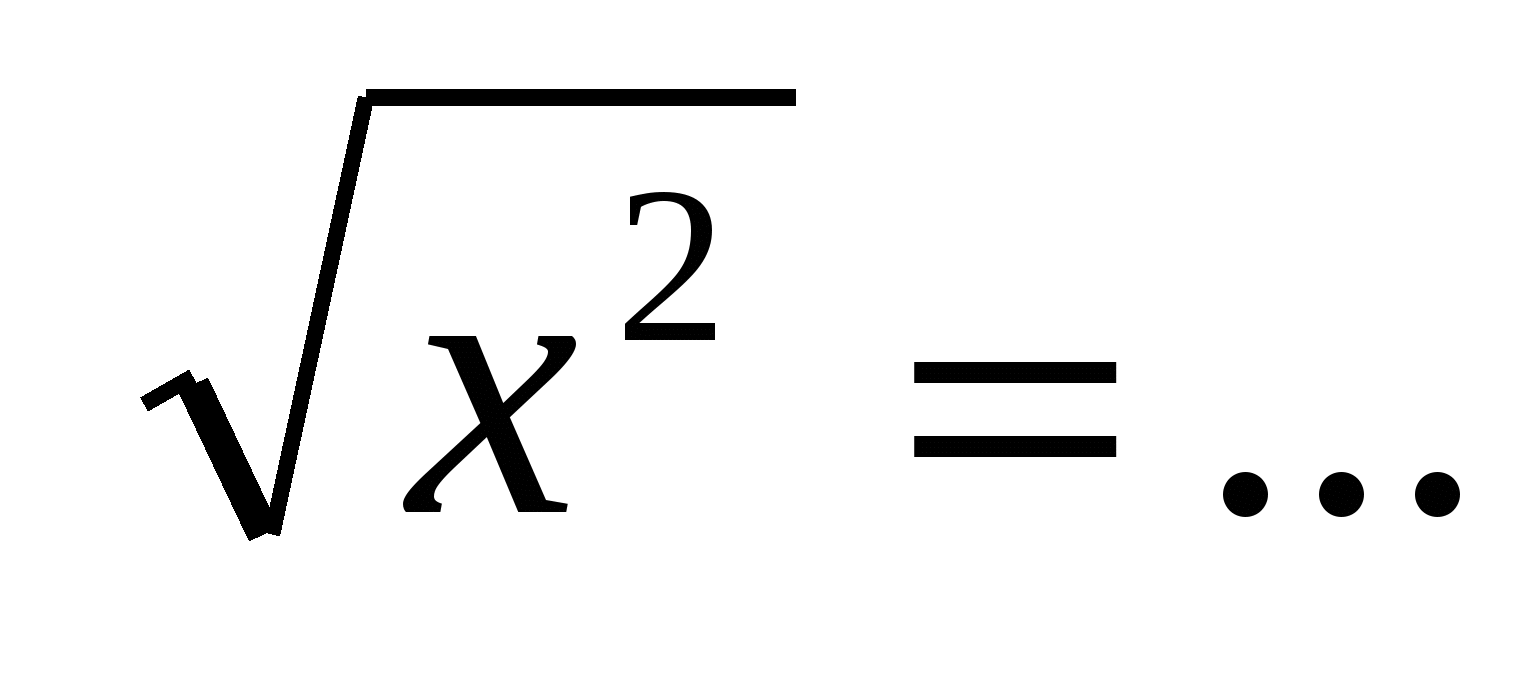
На примере выражения 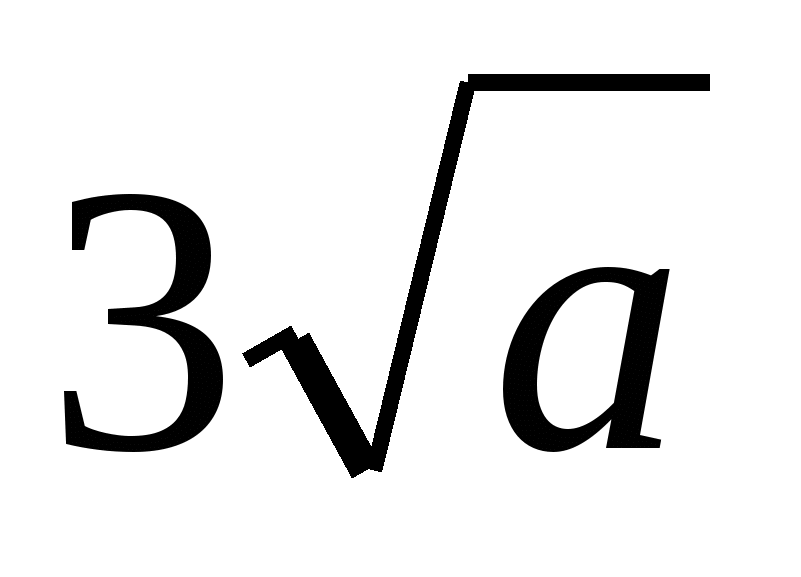 покажите, как можно внести множитель под знак корня. покажите, как можно внести множитель под знак корня.
На примере выражения 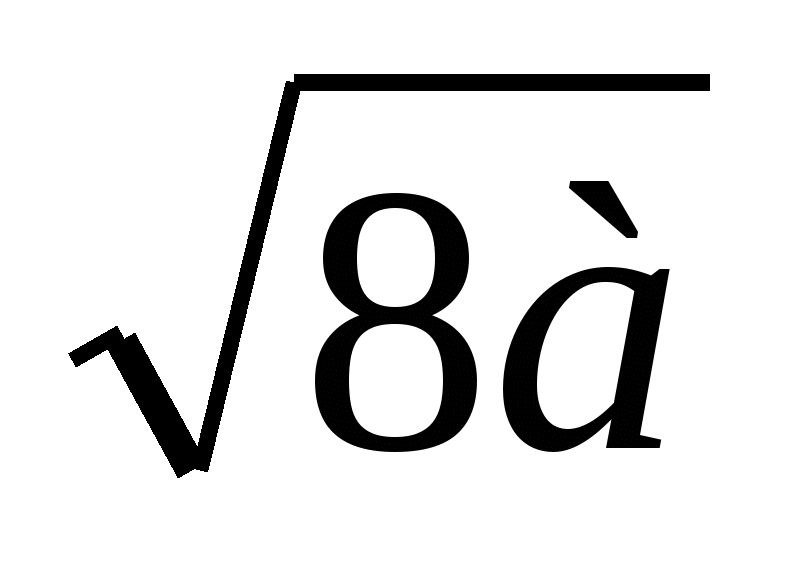 покажите, как можно вынести множитель за знак корня. покажите, как можно вынести множитель за знак корня.
На примере выражений 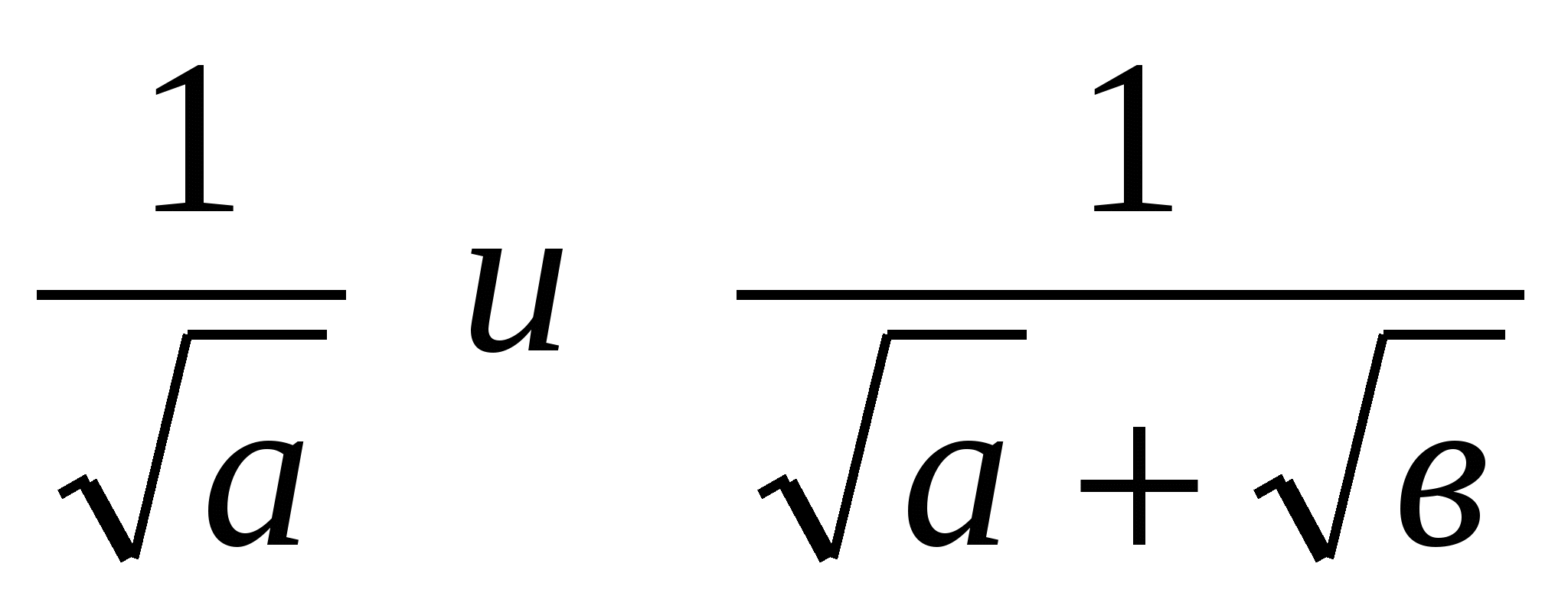 покажите, как можно освободиться от иррациональности в знаменателе дроби. покажите, как можно освободиться от иррациональности в знаменателе дроби.
Что называют дискриминантом квадратного уравнения? Сколько корней может иметь квадратное уравнение?
Напишите формулу корней квадратного уравнения.
Напишите формулу корней квадратного уравнения, в котором второй коэффициент является чётным числом.
Сформулируйте теорему Виета. Чему равны сумма и произведение корней квадратного уравнения ах2 + вх + с = 0 ?
Сформулируйте теорему, обратную теореме Виета.
Приведите пример целого уравнения и пример дробного уравнения.
Сформулируйте теоремы, выражающие основные свойства числовых неравенств.
Сформулируйте теоремы о почленном сложении и умножении неравенств.
Что называется абсолютной погрешностью приближенного значения? Объясните смысл записи х = а + h.
Что называется относительной погрешностью приближенного значения?
Что называется пересечением двух множеств? объединением двух множеств?
Изобразите на координатной прямой числовые промежутки различного вида, назовите и обозначьте их.
Что называется решением неравенства? Что значит решить неравенство?
Что называется решением системы неравенств? Что значит решить систему неравенств?
Сформулируйте определение степени с целым отрицательным показателем.
Сформулируйте свойства произведения и частного степеней с с одинаковыми основаниями и целым показателем.
Как возвести степень в степень?
Как возвести произведение и частное в степень?
Какую запись числа называют его стандартным видом?
Объясните на примере, как по таблице частот находят среднее арифметическое, размах и моду.
Какие способы наглядного представления информации вам известны? Объясните, в чём состоит каждый из этих способов.
Что называется гистограммой? Как изображается на гистограмме общий объём исследуемой совокупности?
Перечень контрольных работ по модулям.
Рациональные дроби и их свойства – 2.
Квадратные корни – 2.
Квадратные уравнения – 2.
Неравенства – 2.
Степень с целым показателем – 1.
Перечень практических работ.
Пересечение и объединение множеств.
Составление и решение приведенных квадратных уравнений с помощью теоремы Виета и обратной теоремы.
Сбор, группировка и наглядное представление статистической информации на местном материале.
Итоговый контроль.
Вариант 1
Часть 1. Указать номер правильного ответа.
1
|
Найти абсолютную погрешность числа 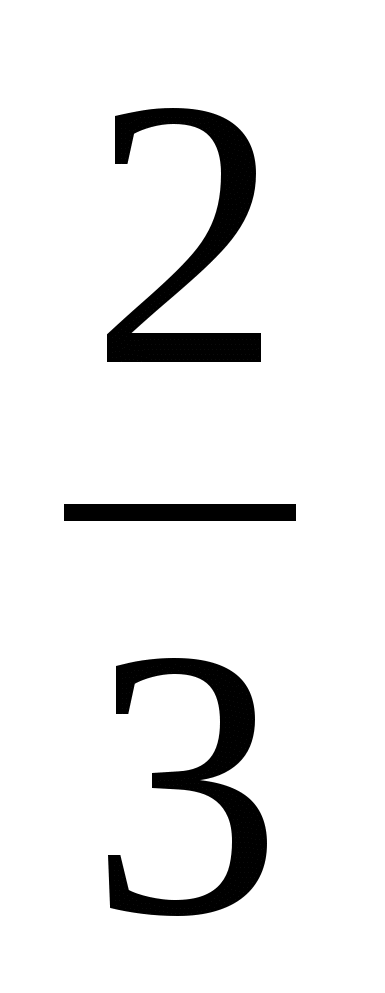 числом 0,7. числом 0,7.
|
1) -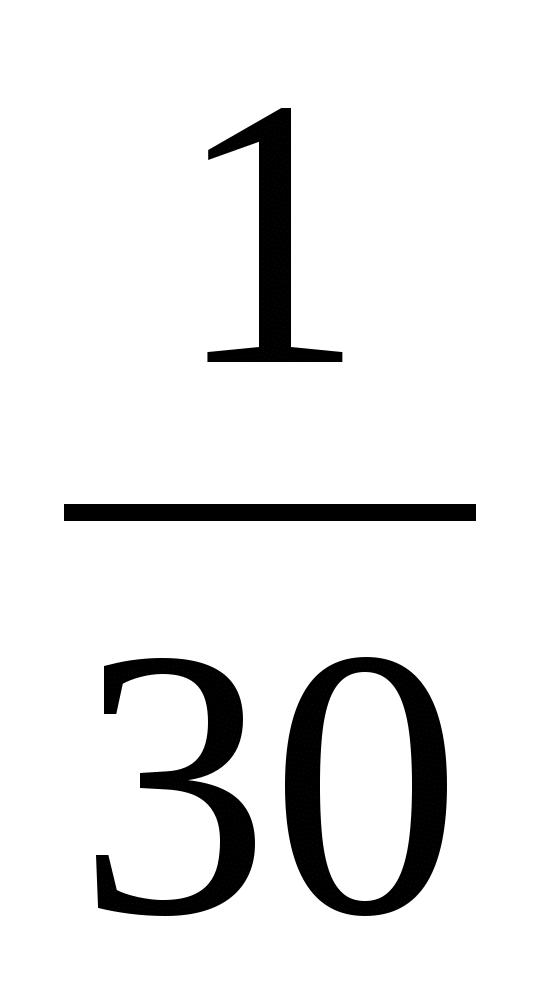
|
2) 0,033
|
3) 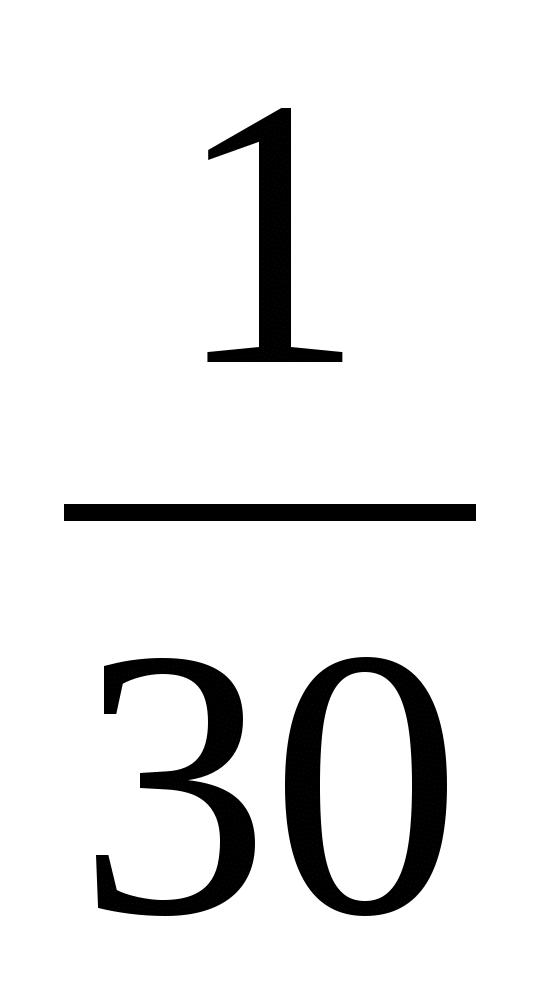
|
4)0,03
|
2
|
Записать число 420,01 в стандартном виде.
|
1) 4,2001*102
|
1) 0,42001*103
|
1) 42001*10-2
|
1) 4 20
|
3
|
Сравнить x с нулем, если - a2x > 0.
|
1) x < 0
|
2) x > 0
|
3) x = 0
|
4) нельзя сравнить
|
4
|
Решить уравнение (x –1)(x + 3) = 0.
|
1) x1=-1, x2=3
|
2) x1= 1, x2=3
|
3) x1=-1, x2=-3
|
4) x1= 1, x2=-3
|
5
|
Решить уравнение 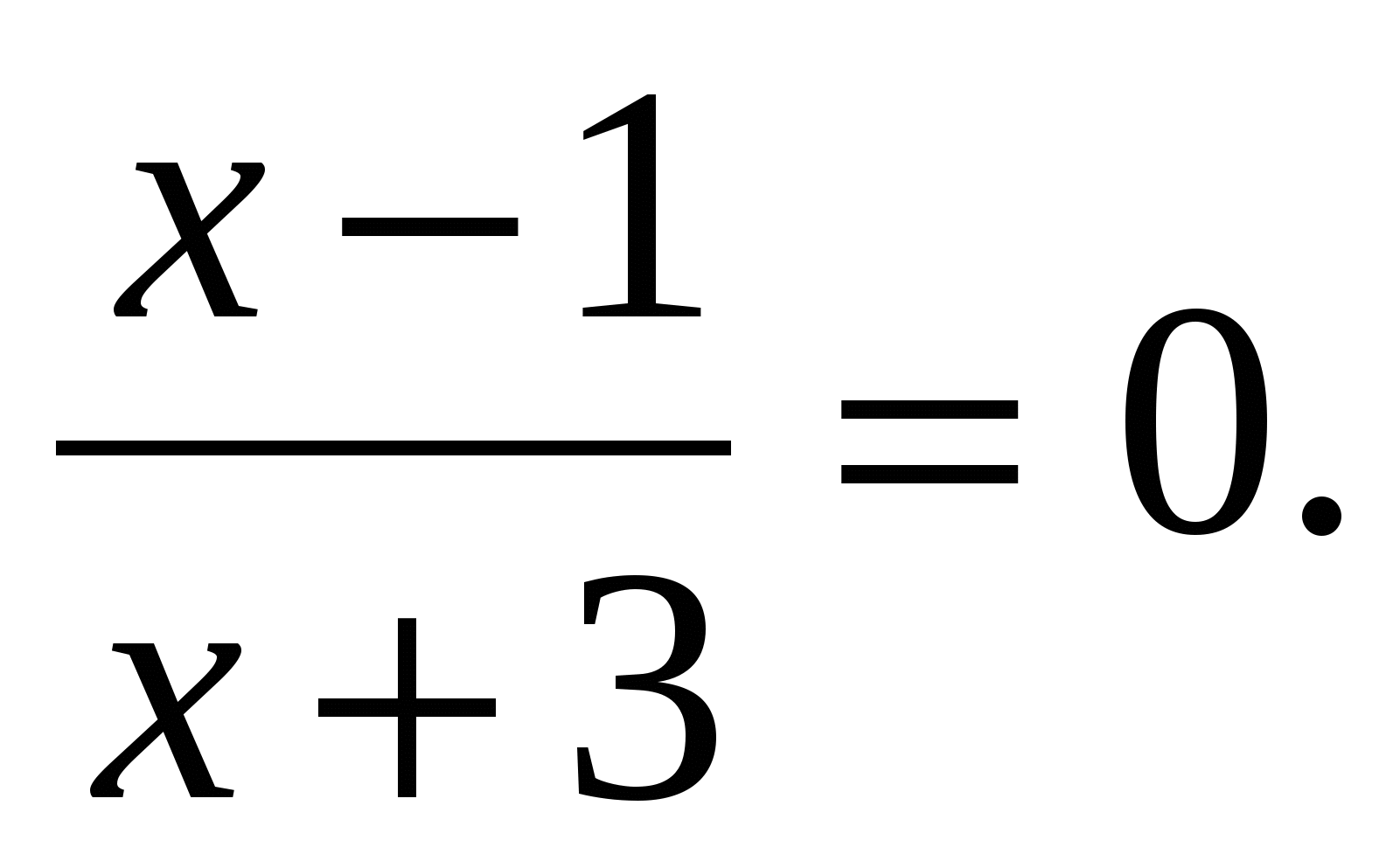
|
1) x =1
|
2) x1= 1, x2=-3
|
3) x =-3
|
4) нет корней
|
6
|
Решить неравенство 2x –3 > -5.
|
1) x < -1
|
2) x > -8
|
3) x > -4
|
4) x > -1
|
7
|
Решить неравенство 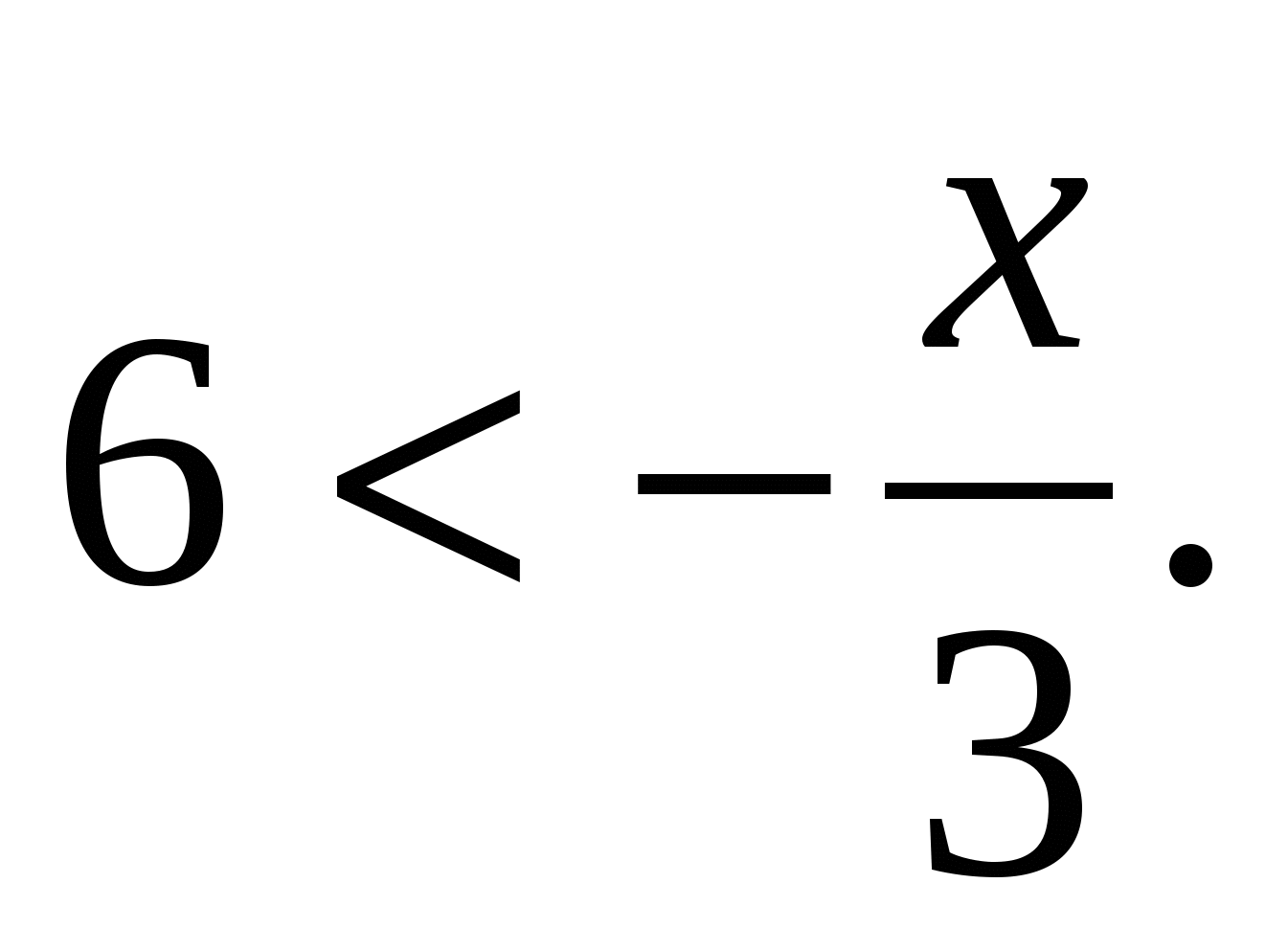
|
1) x < -2
|
2) x > -2
|
3) x < -18
|
4) x > -18
|
8
|
Указать наибольшее целое число, являющееся решением неравенства 2x + 7 < 1.
|
1) -3
|
2) -4
|
3) -2
|
4) 0
|
9
|
Решить систему неравенств 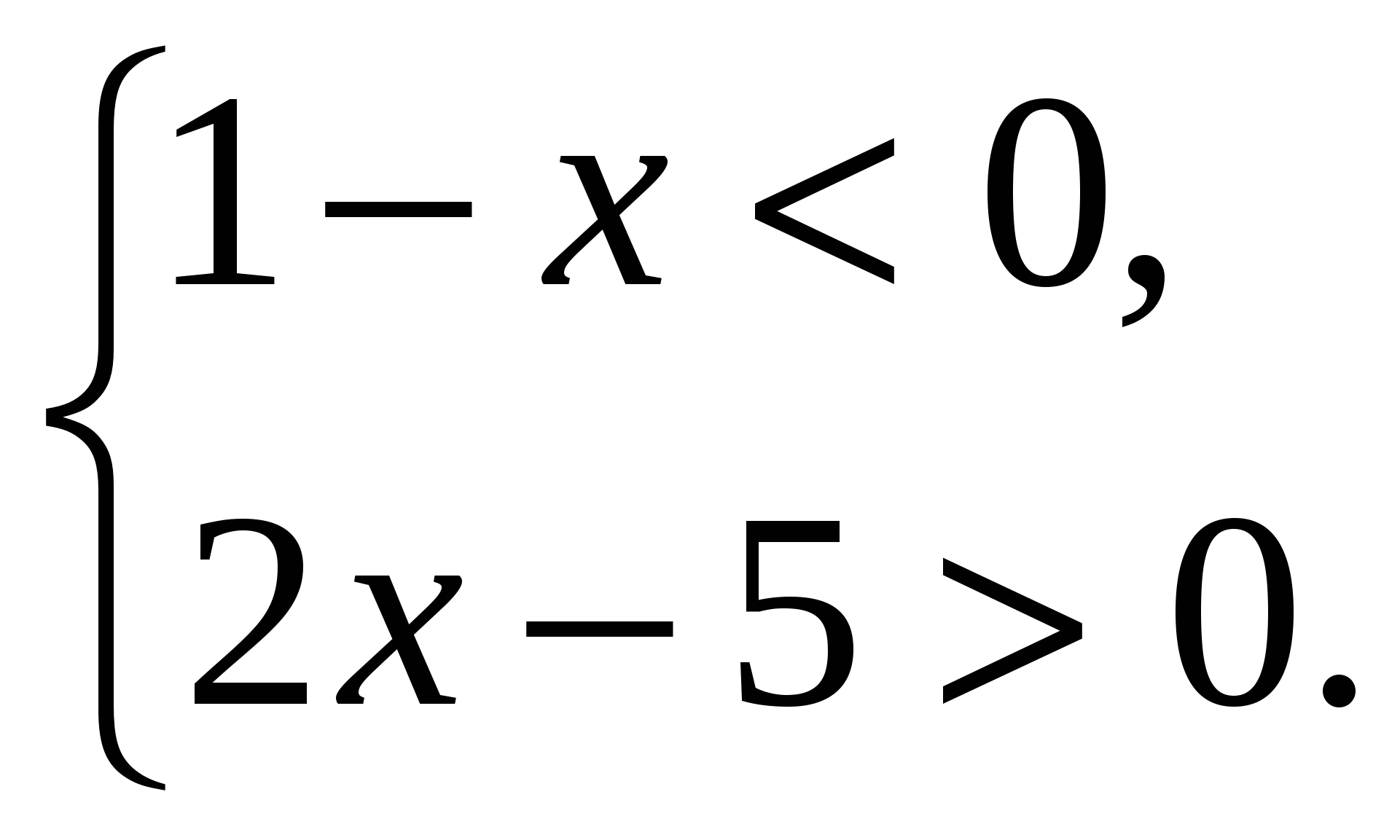
|
1) (2,5; 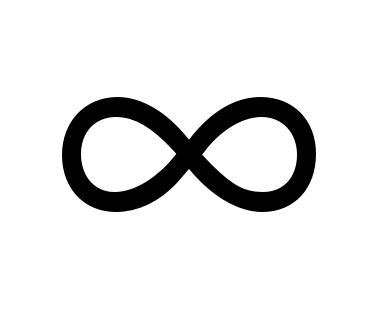 ) )
|
2) (1; 2,5)
|
3) (1; 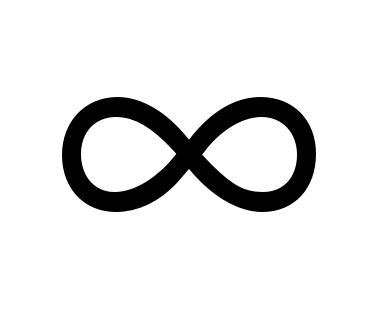 ) )
|
4) решений нет
|
10
|
Сколько целых решений имеет неравенство -2 < x 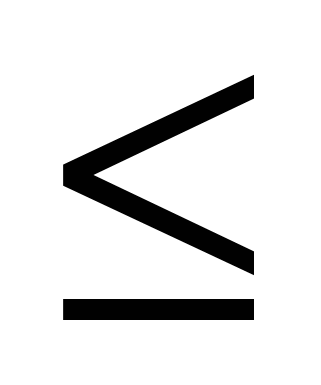 1. 1.
|
1) 1
|
2) 2
|
3) 3
|
4) 4
|
11
|
Решить уравнение 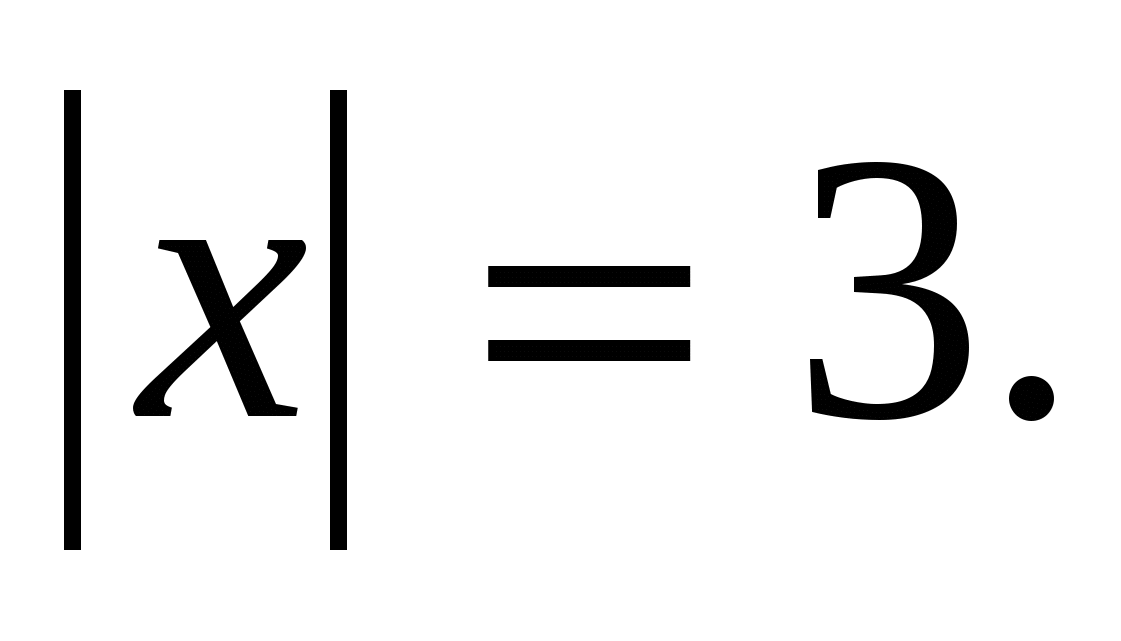
|
1) 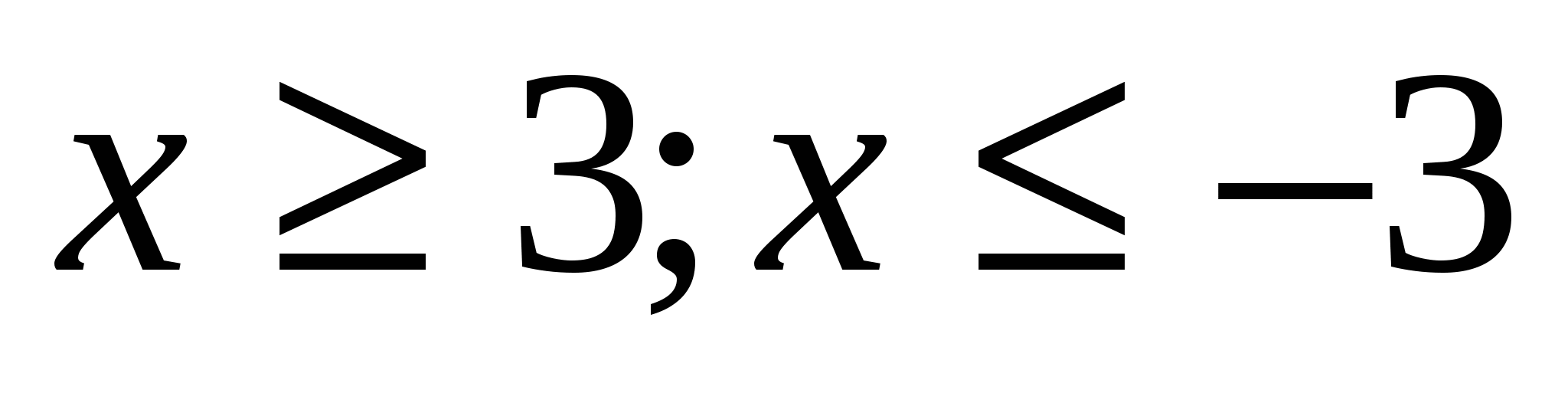
|
2) 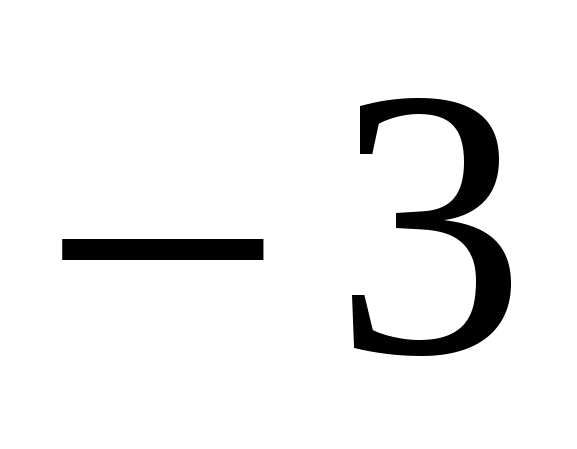 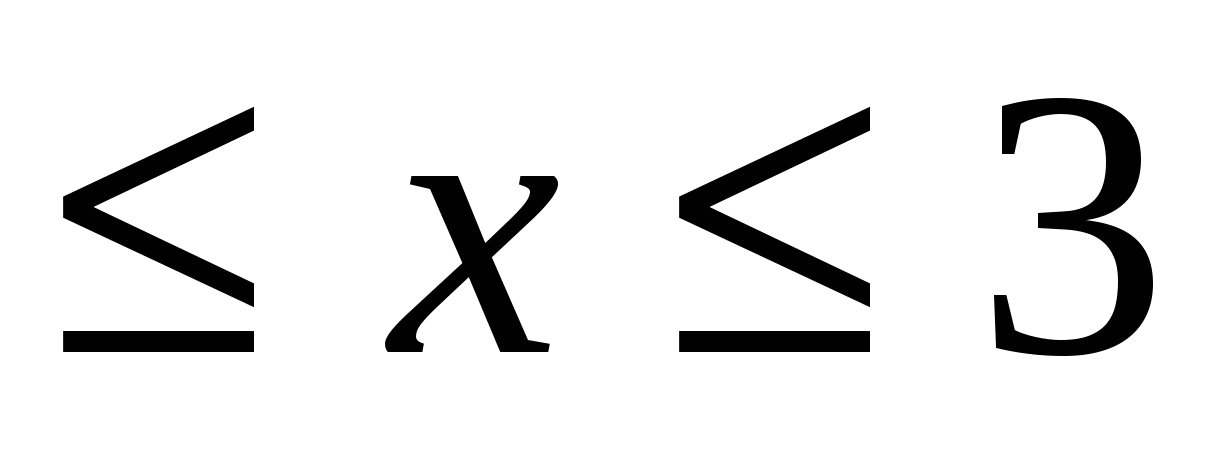
|
3) x =3
|
4) x  = = 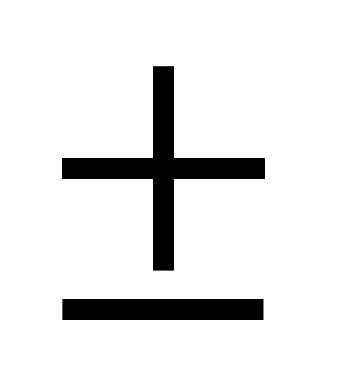 3 3
|
12
|
Решить уравнение 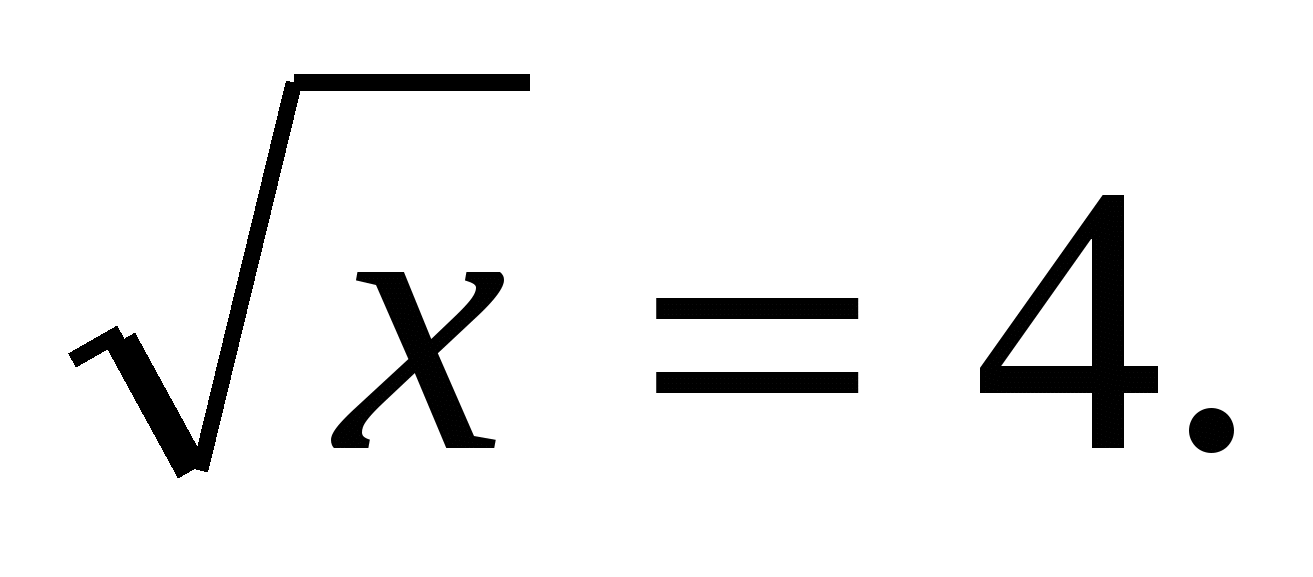
|
1) x = 2
|
2) x = 16
|
3) x = 8
|
4) x = 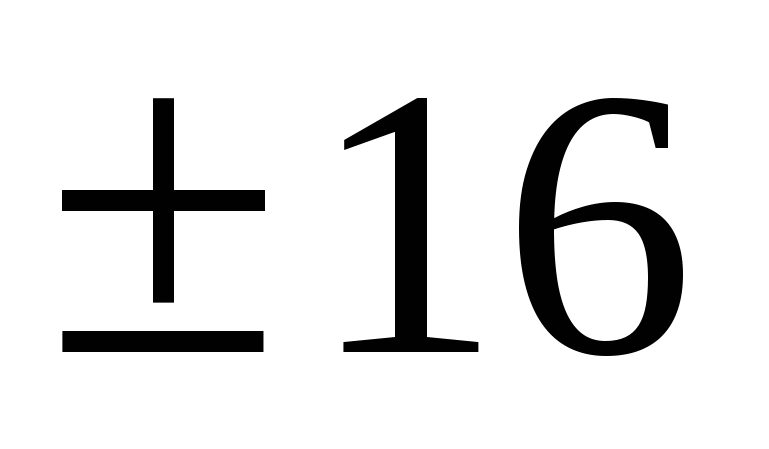
|
13
|
Вычислить 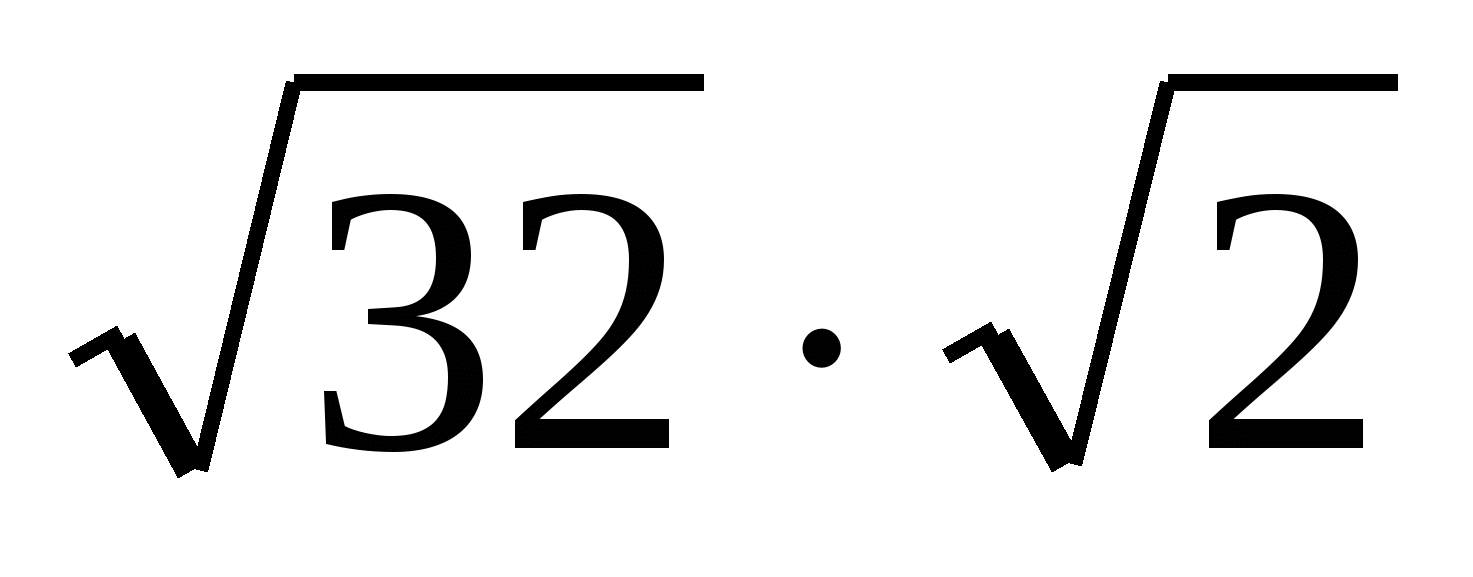 . .
|
1) 4
|
2) 16
|
3) 16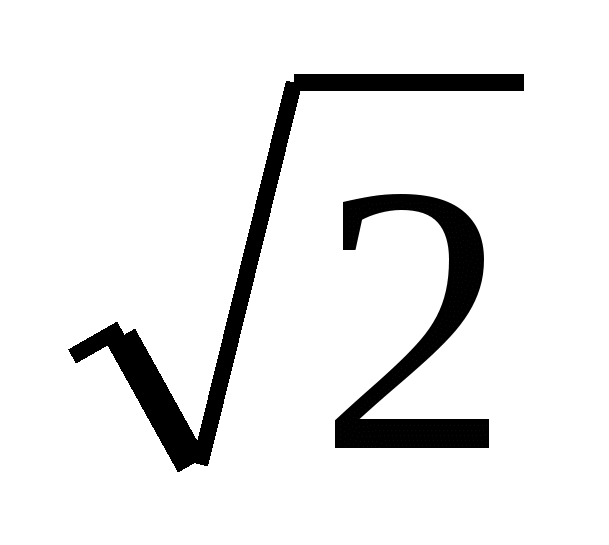
|
4) 8
|
14
|
Вычислить 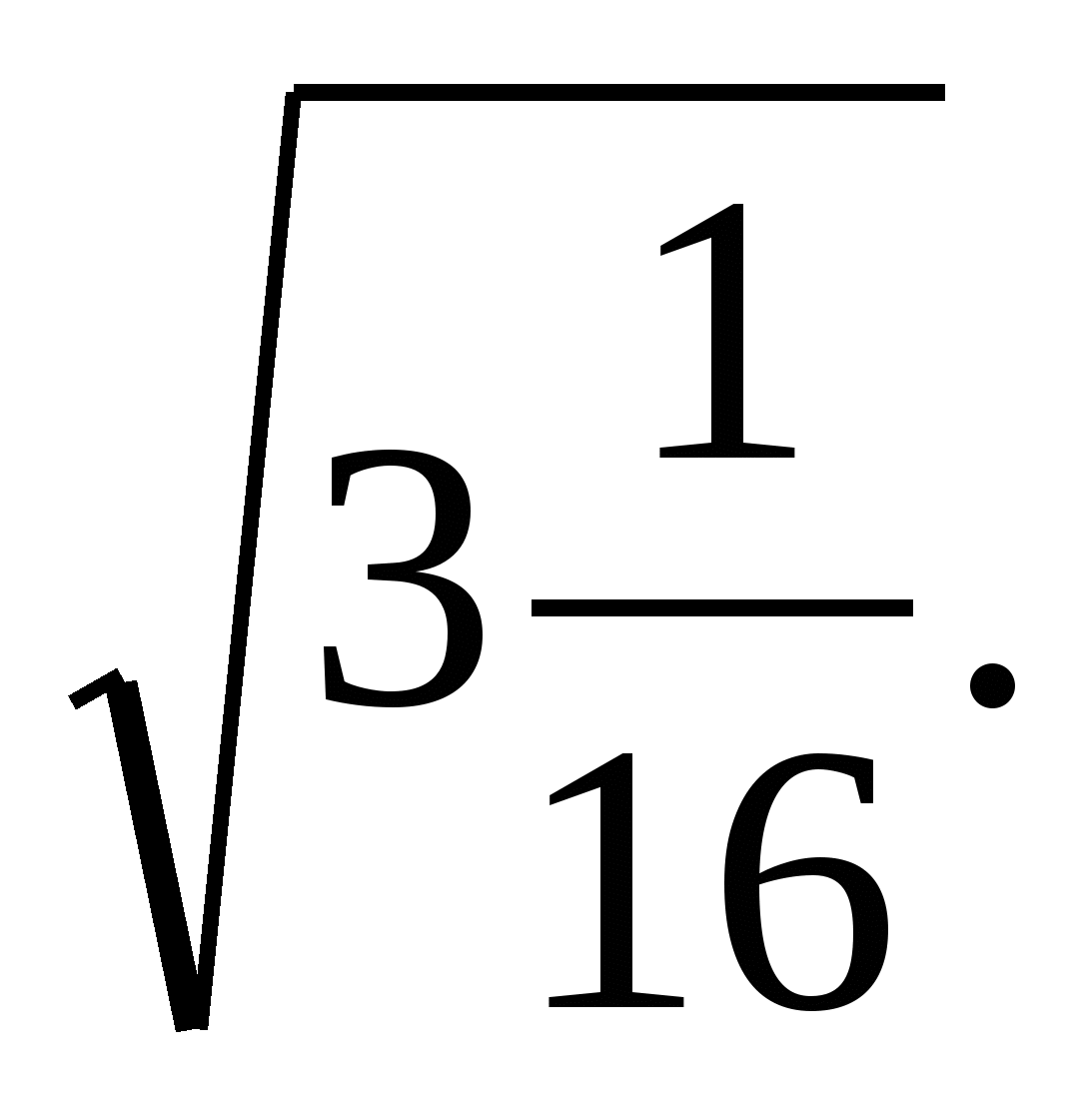
|
1) 1,75
|
2) 3,25
|
3) 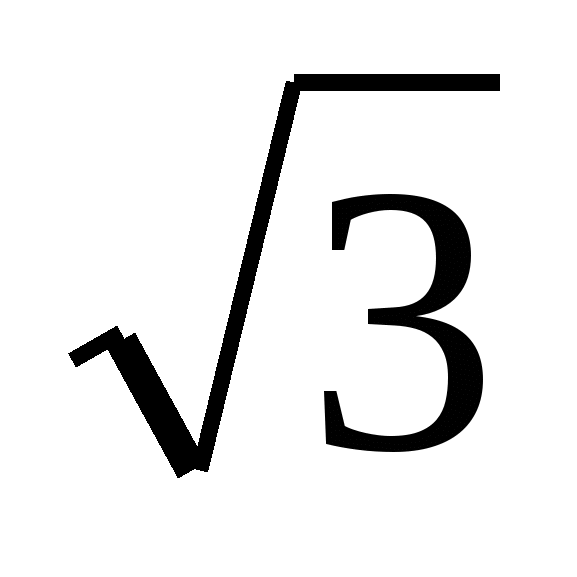 + 0,25 + 0,25
|
4) 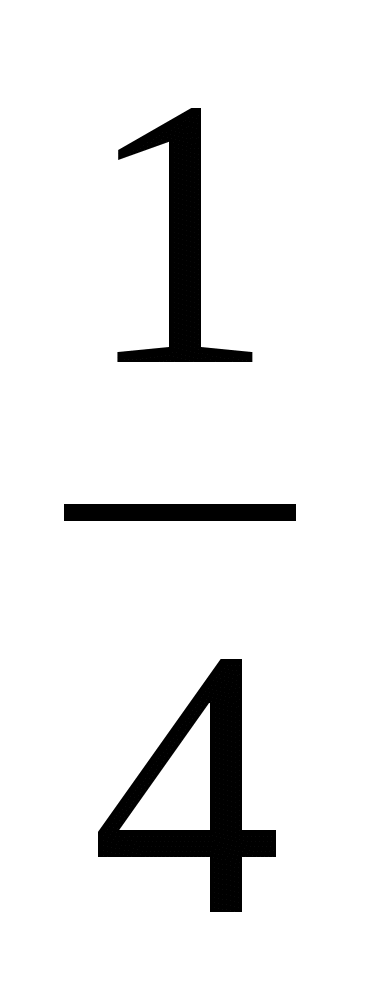 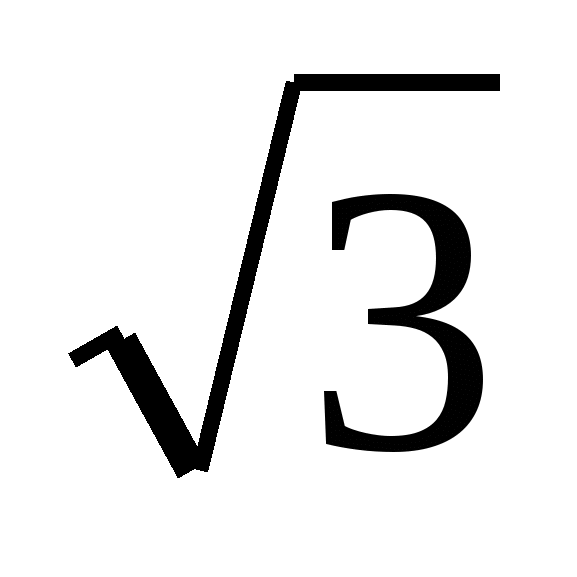
|
15
|
Вынести множитель из-под знака корня 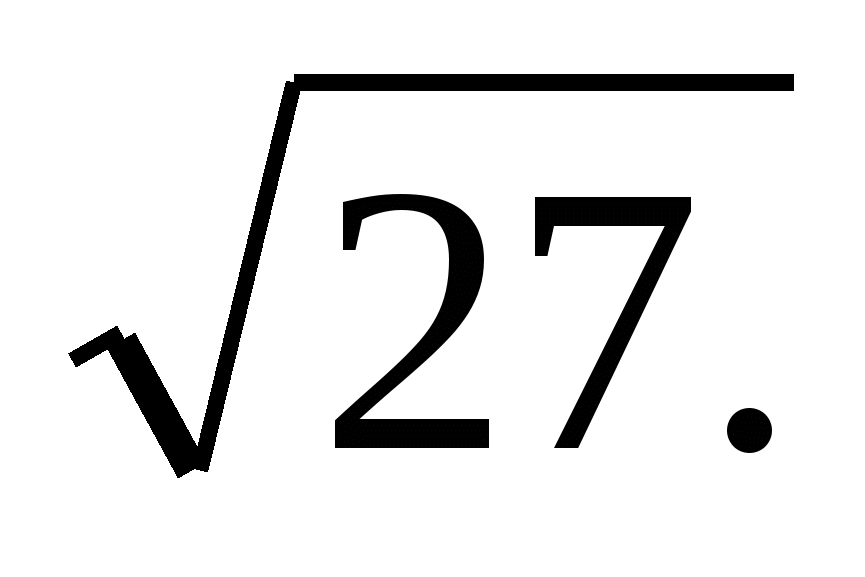
|
1) 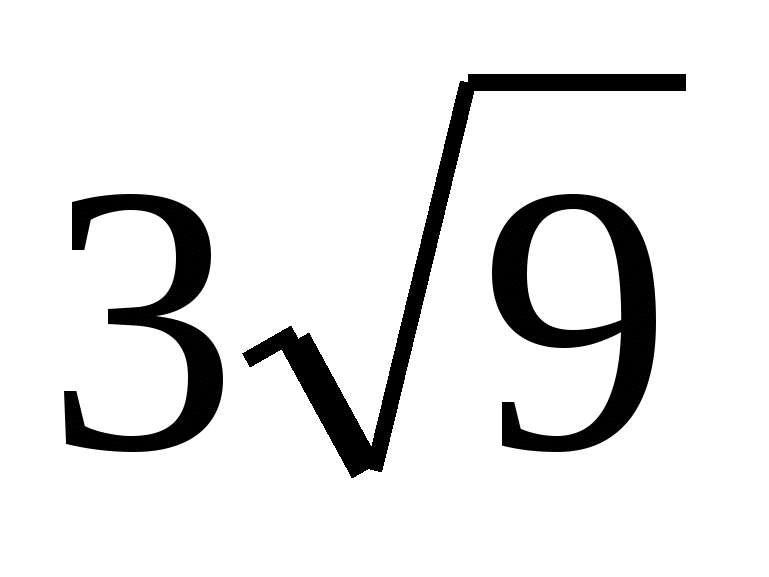
|
2) 9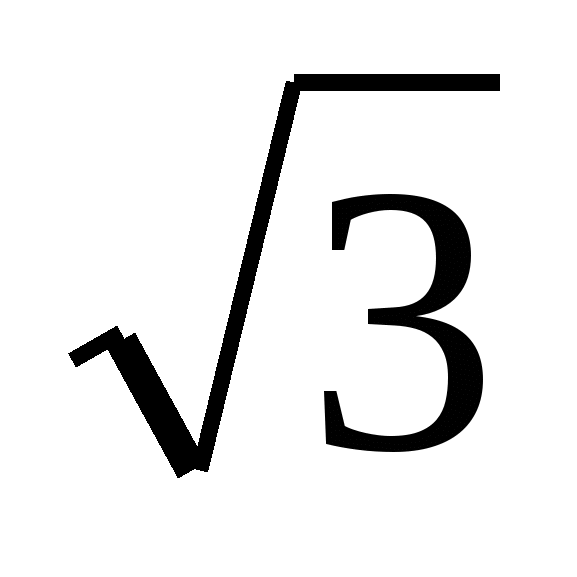
|
3) 3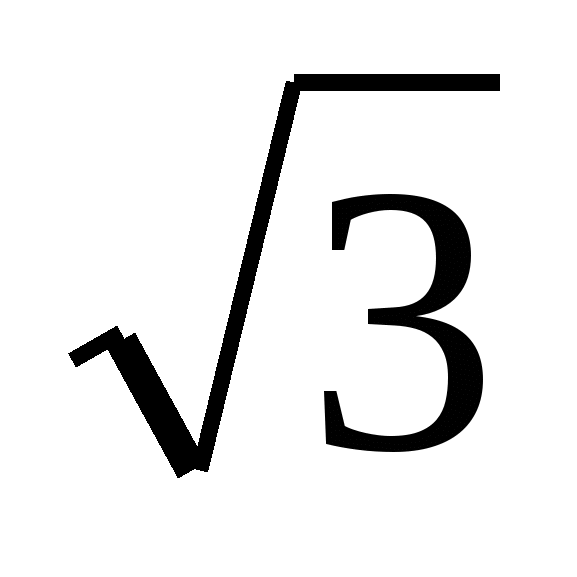
|
4) 3
|
16
|
Внести множитель под знак корня -3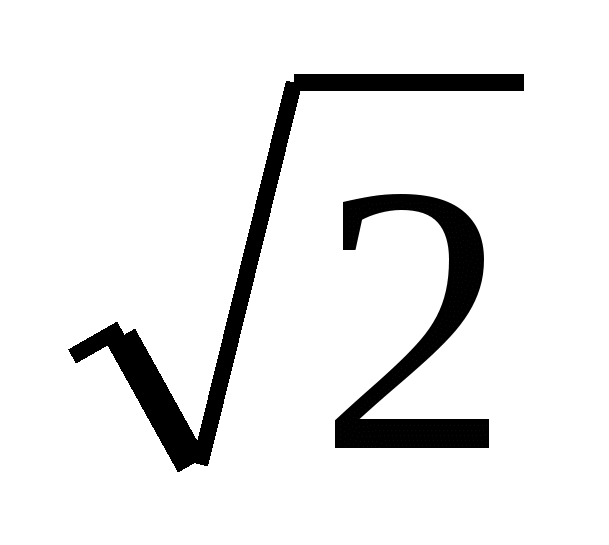 . .
|
1) 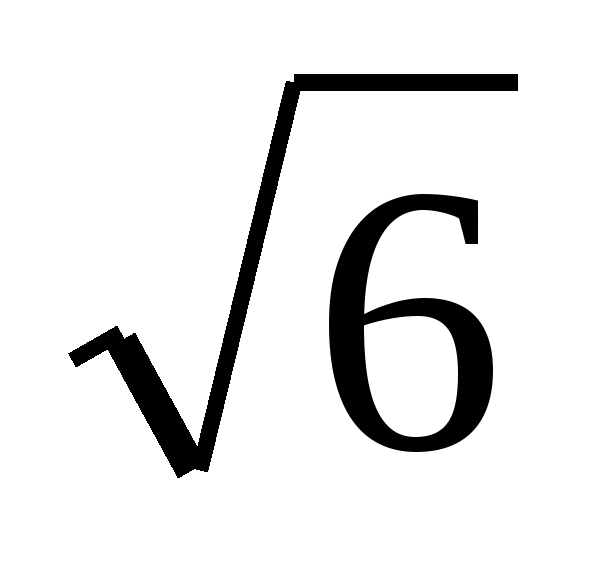
|
2) -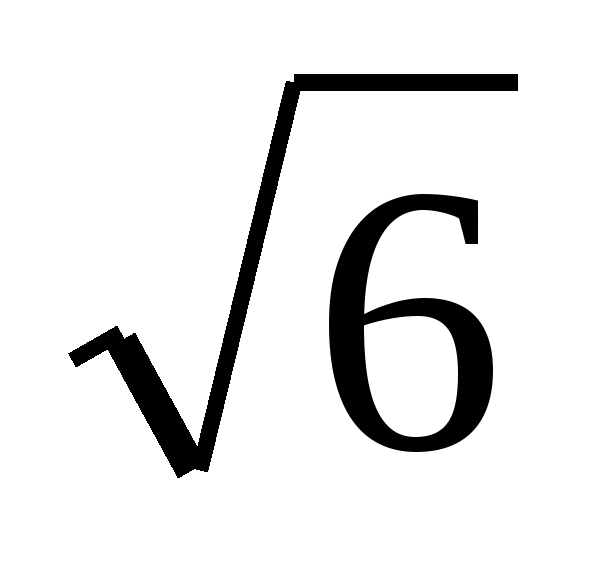
|
3) 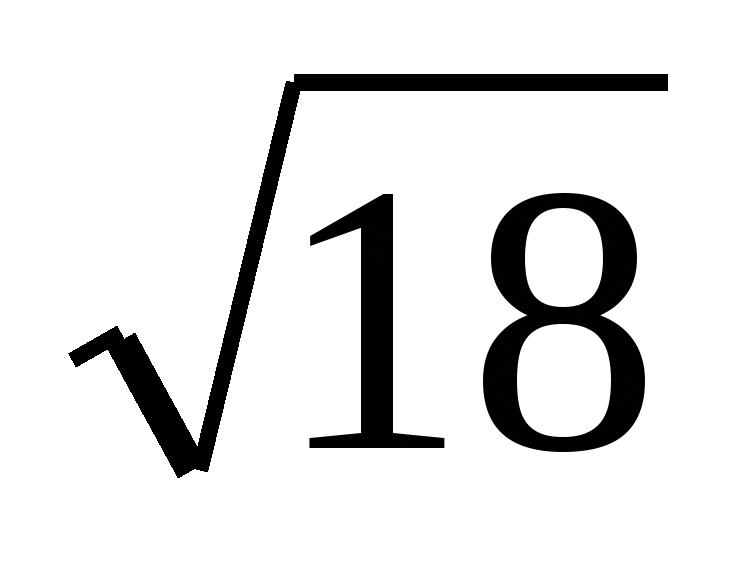
|
4) -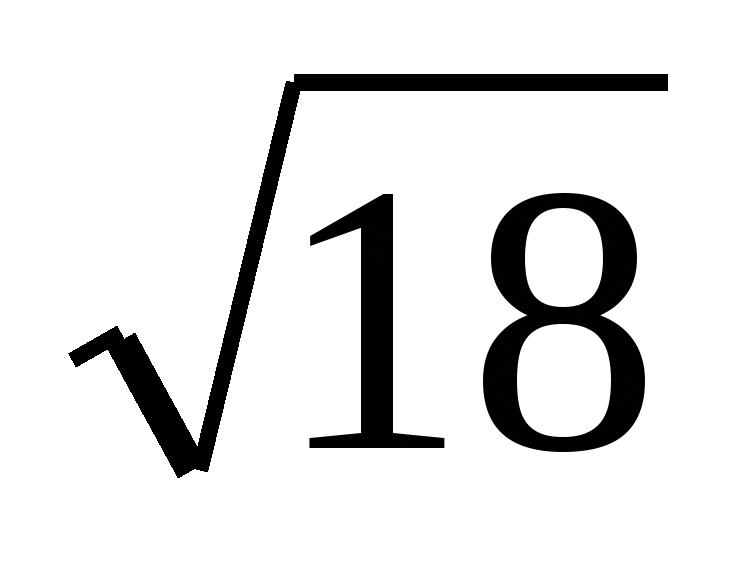
|
17
|
Решить уравнение x2 =36
|
1) 6
|
2) 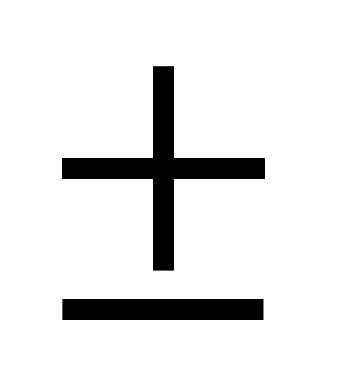 6 6
|
3) 18
|
4) 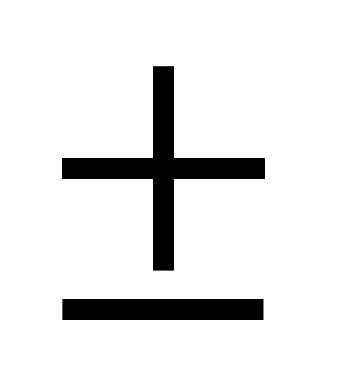 18 18
|
18
|
Найти корни уравнения x2 – x = 0.
|
1) 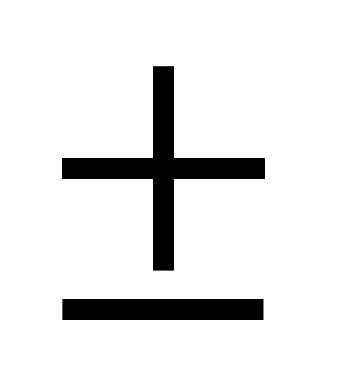 1; 0 1; 0
|
2) 1; 0
|
3) –1; 0
|
4) 0
|
19
|
Решить уравнение 3x2 – 8x – 3 = 0
|
1) 3; 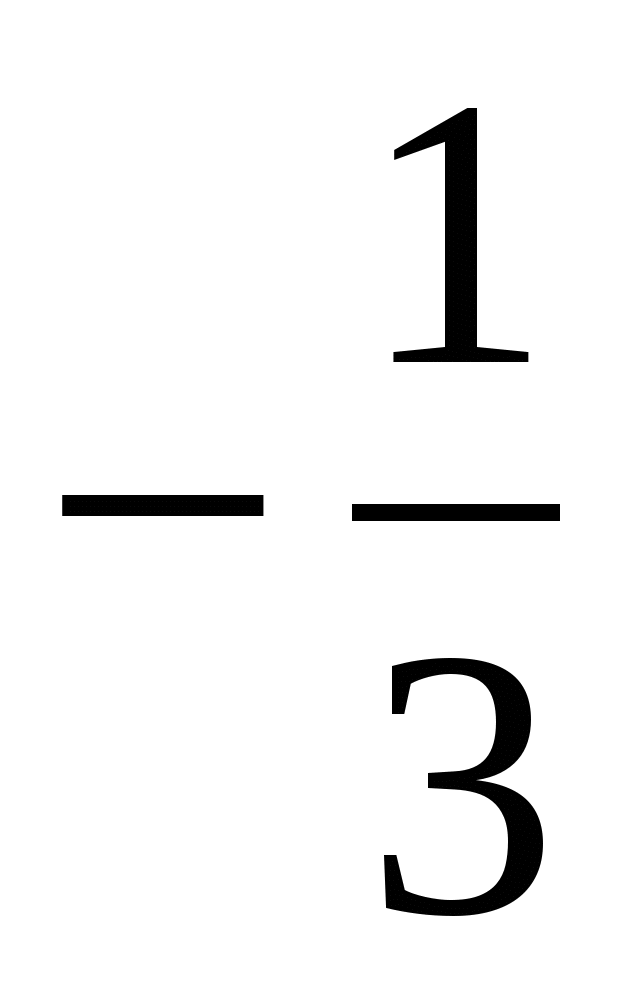
|
1) -3; 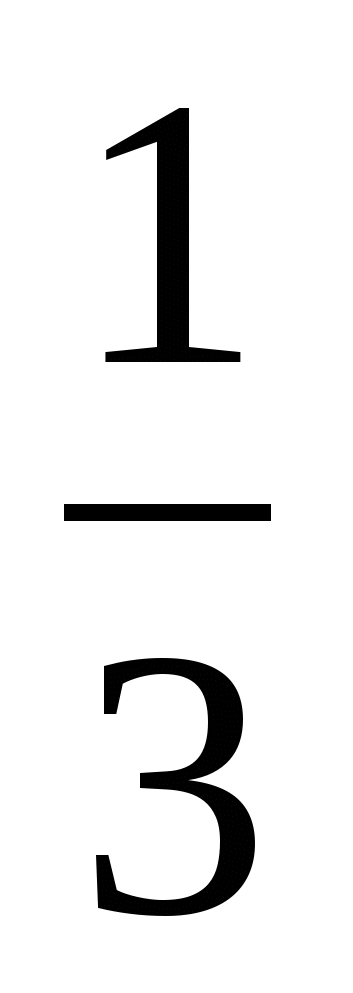
|
3) 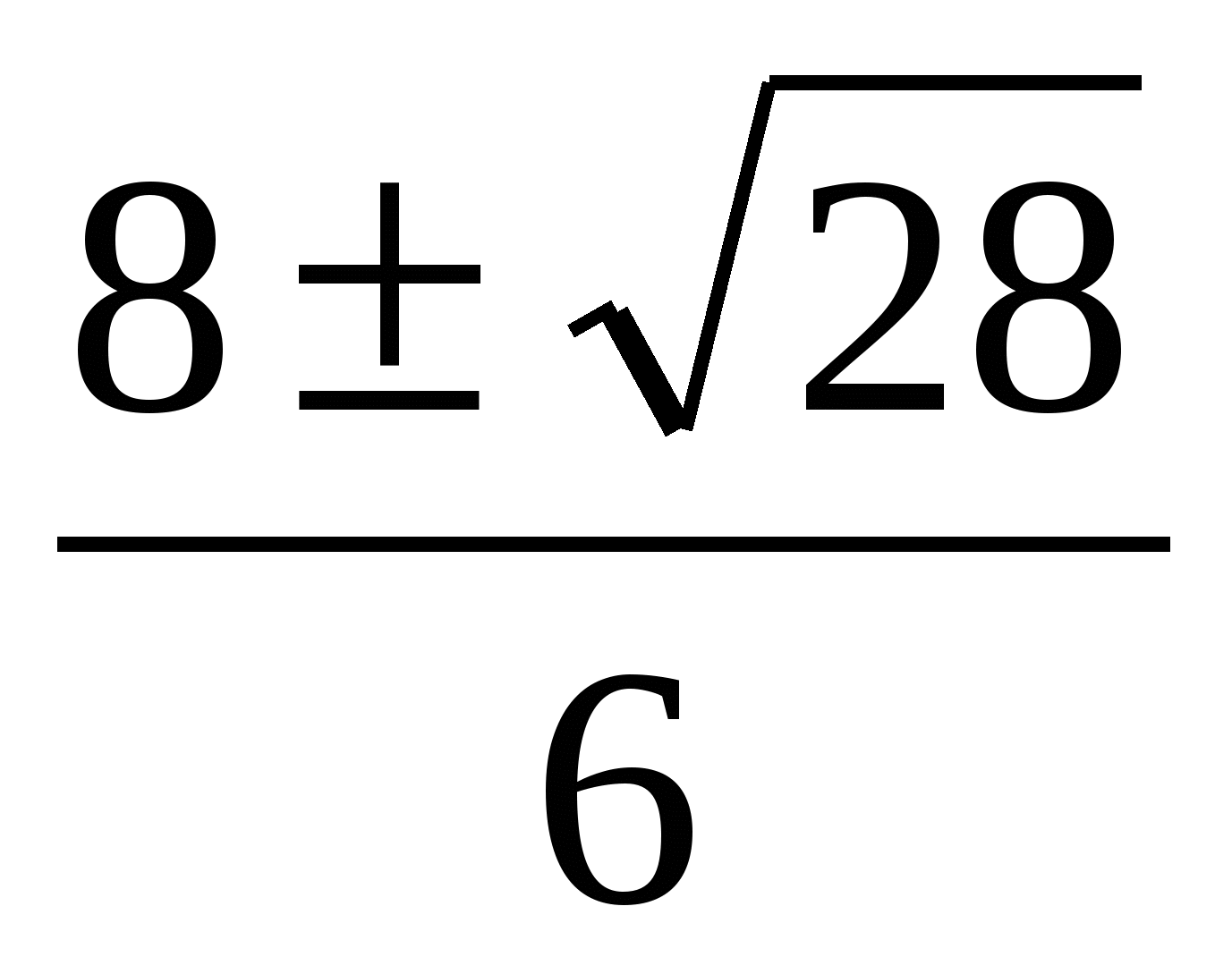
|
4) нет корней
|
20
|
По теореме Виета найти сумму корней приведенного квадратного уравнения
x2 – 5x + 3 = 0.
|
1) -3
|
2) 5
|
3) -5
|
4) 3
|
Часть 2. Записать решение.
Доказать, что для любых неотрицательных x справедливо неравенство 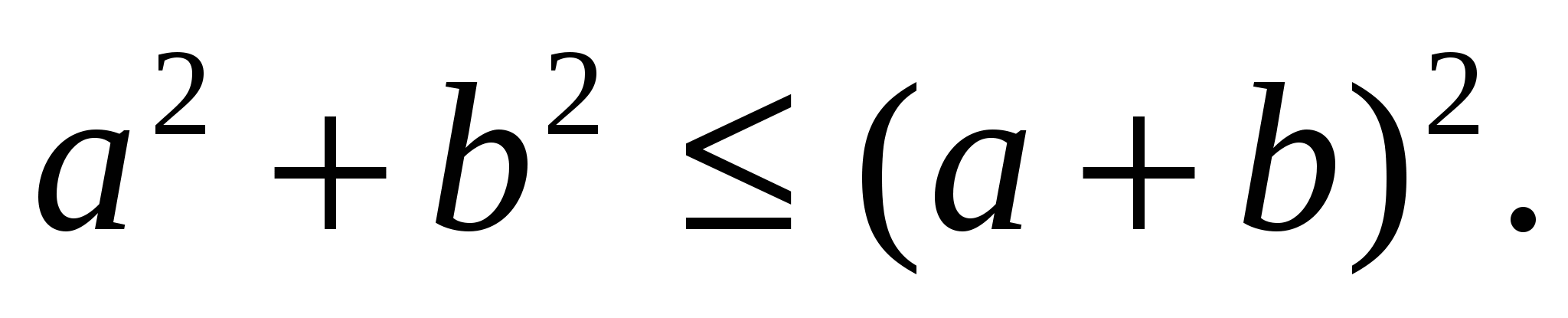
Вычислить 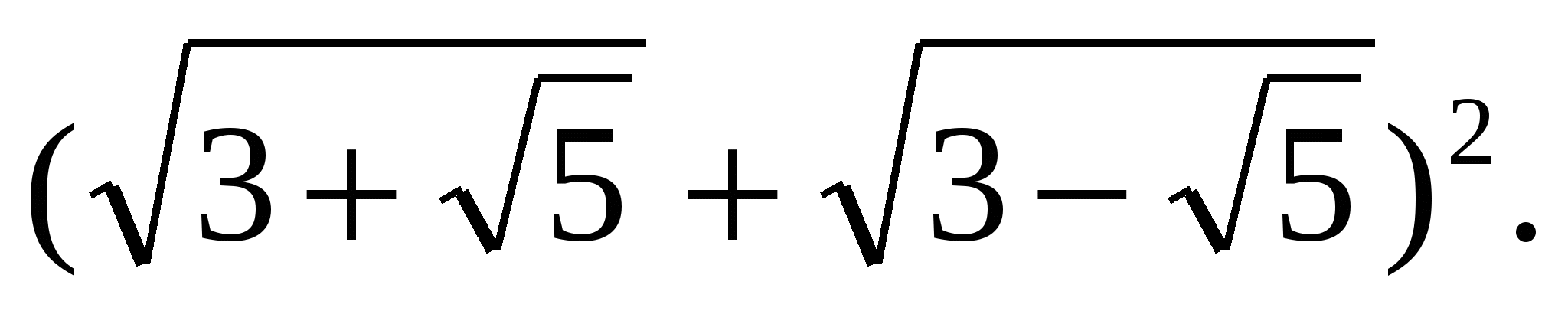
Решить уравнение 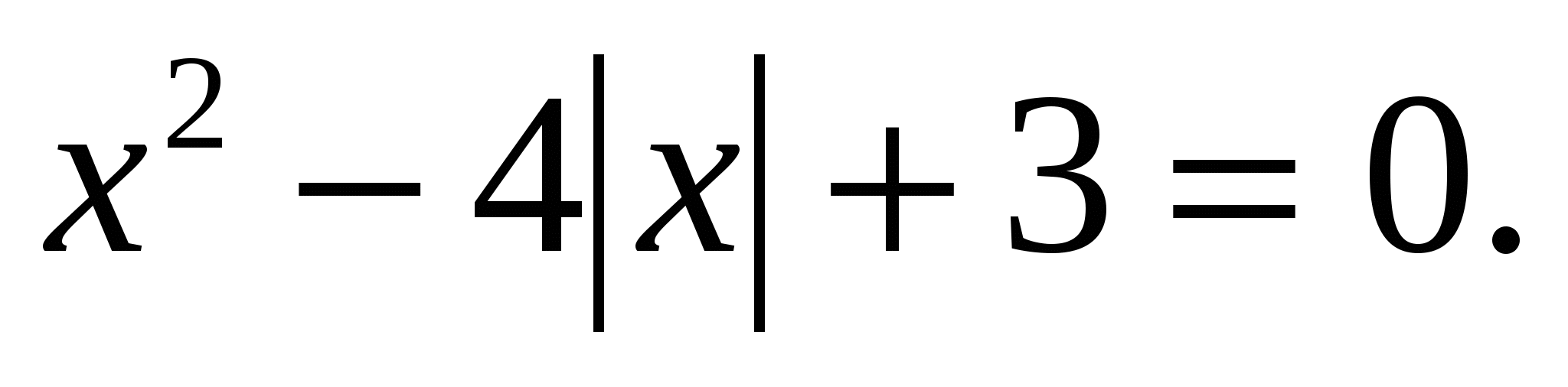
Вариант 2
Часть 1. Указать номер правильного ответа.
1
|
Найти абсолютную погрешность числа 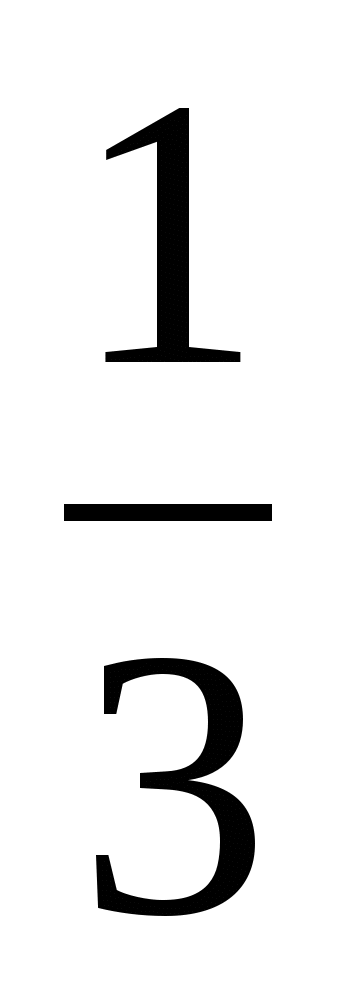 числом 0,3. числом 0,3.
|
1) -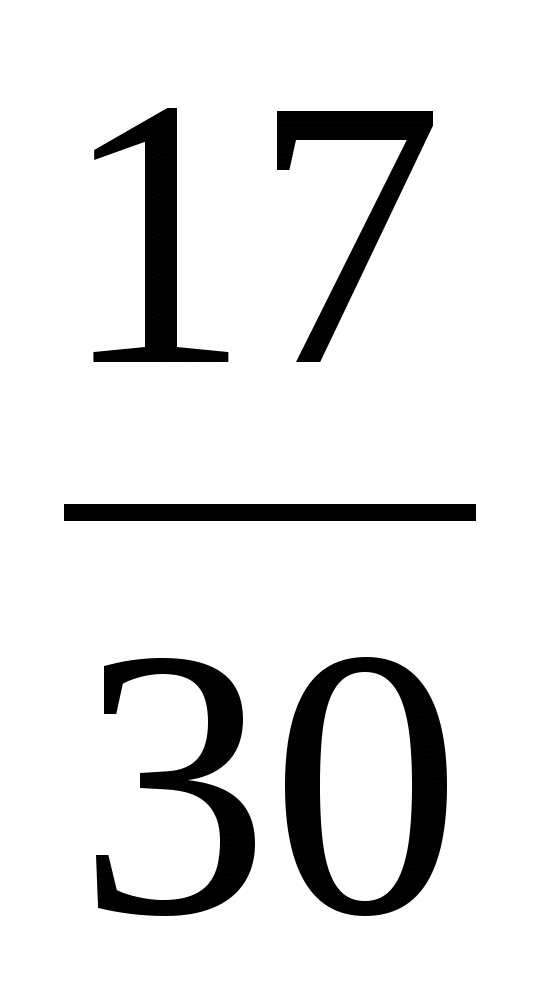
|
2) 0,033
|
3) 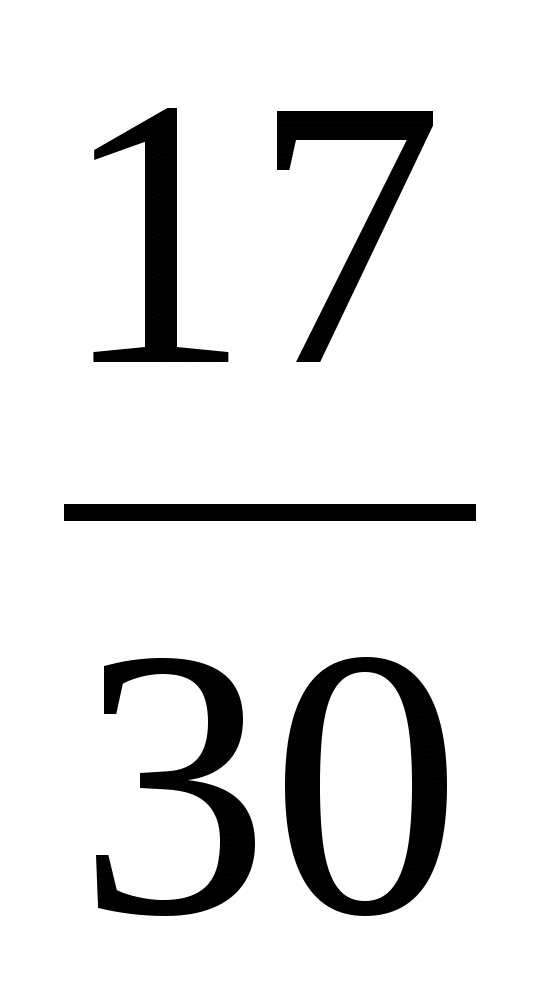
|
4)0,03
|
2
|
Записать число 564,01 в стандартном виде.
|
1) 5,6401*102
|
1) 0,56401*103
|
1) 56401*10-2
|
1) 564
|
3
|
Сравнить x с нулем, если a2x > 0.
|
1) x < 0
|
2) x > 0
|
3) x = 0
|
4) нельзя сравнить
|
4
|
Решить уравнение (x –5)(x +13) = 0.
|
1) x1=-5, x2=13
|
2) x1= 5, x2=13
|
3) x1=-5, x2=-13
|
4) x1= 5, x2=-13
|
5
|
Решить уравнение 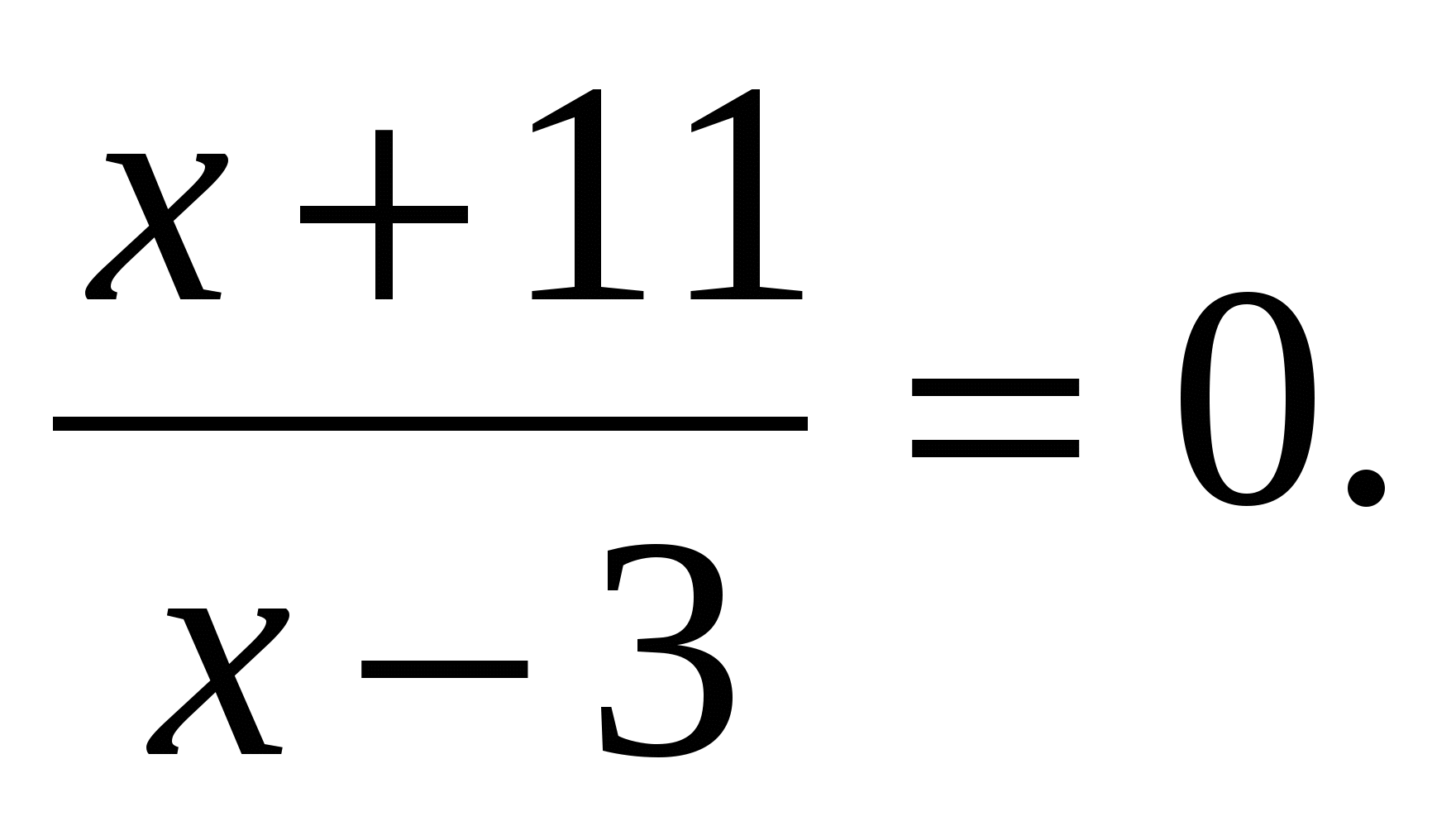
|
1) x =-11
|
2) x1= 11, x2=-3
|
3) x = 3
|
4) нет корней
|
6
|
Решить неравенство 2x –23 > -5.
|
1) x < 14
|
2) x > 9
|
3) x > -9
|
4) x > -14
|
7
|
Решить неравенство 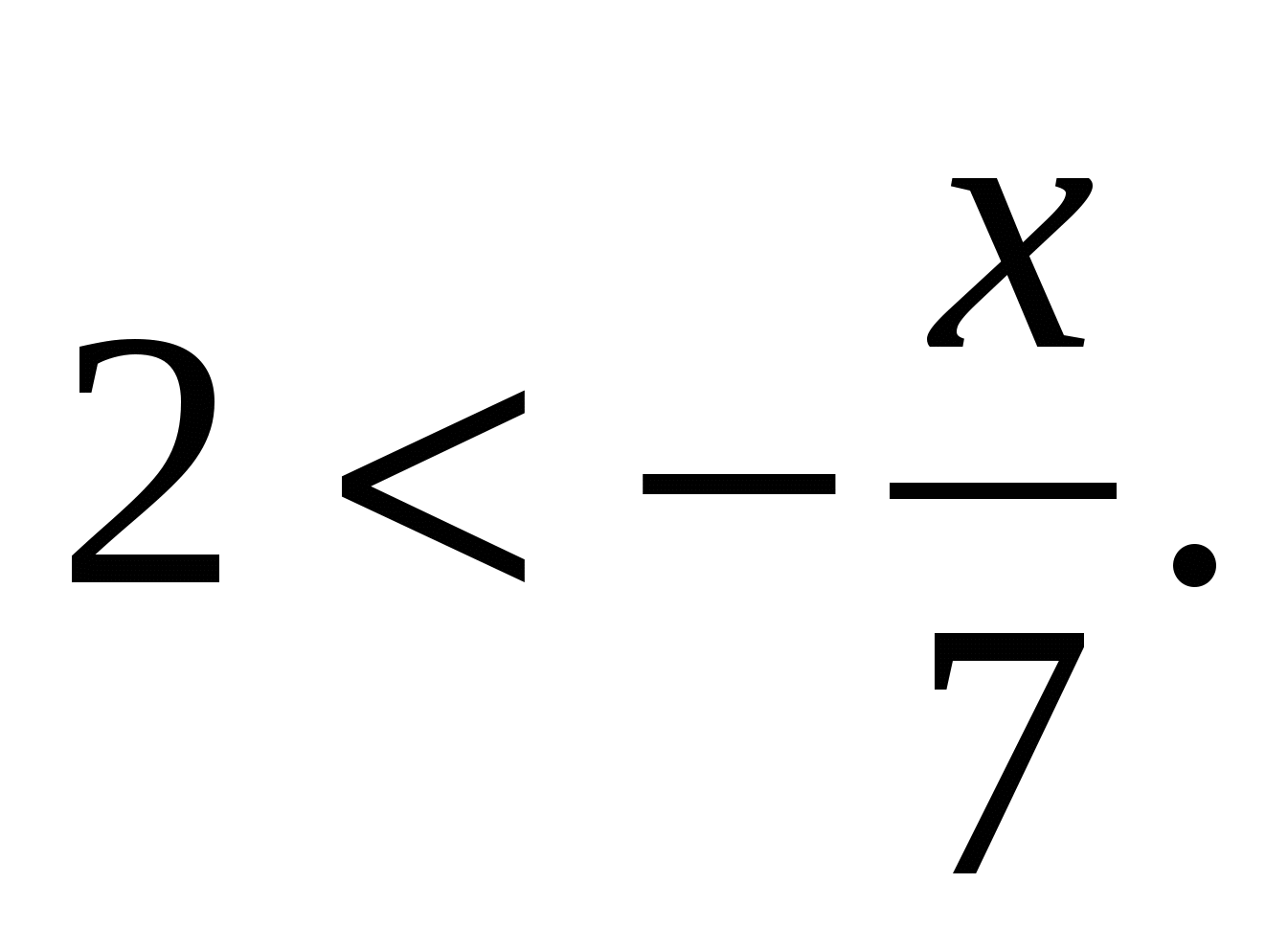
|
1) x < -2
|
2) x > -2
|
3) x < -14
|
4) x > -14
|
8
|
Указать наибольшее целое число, являющееся решением неравенства 2x - 7 < 1.
|
1) 3
|
2) 4
|
3) 2
|
4) 0
|
9
|
Решить систему неравенств 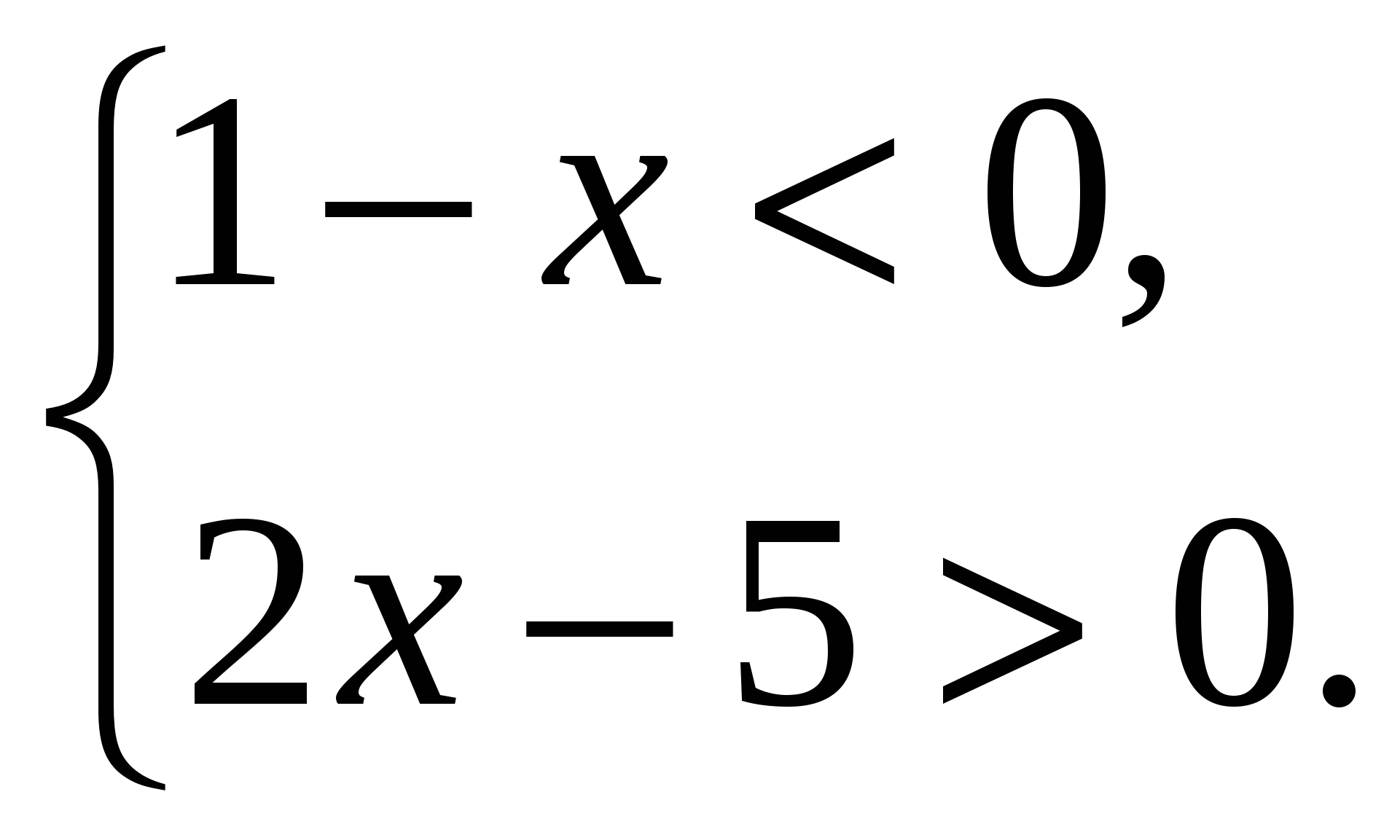
|
1) (2,5; 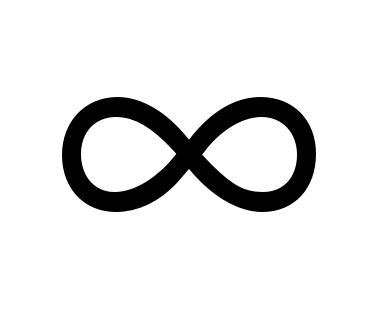 ) )
|
2) (1; 2,5)
|
3) (1; 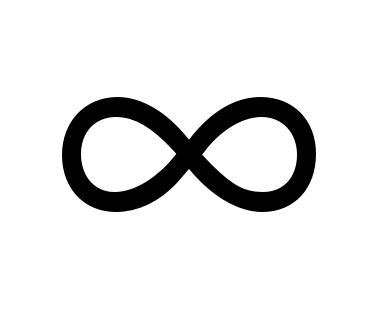 ) )
|
4) решений нет
|
10
|
Сколько целых решений имеет неравенство -1 < x 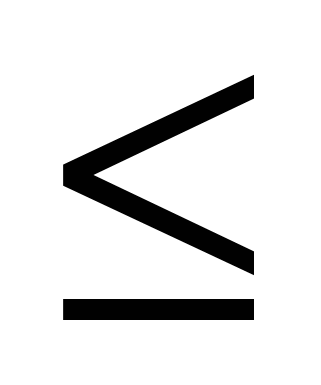 2. 2.
|
1) 1
|
2) 2
|
3) 3
|
4) 4
|
11
|
Решить уравнение 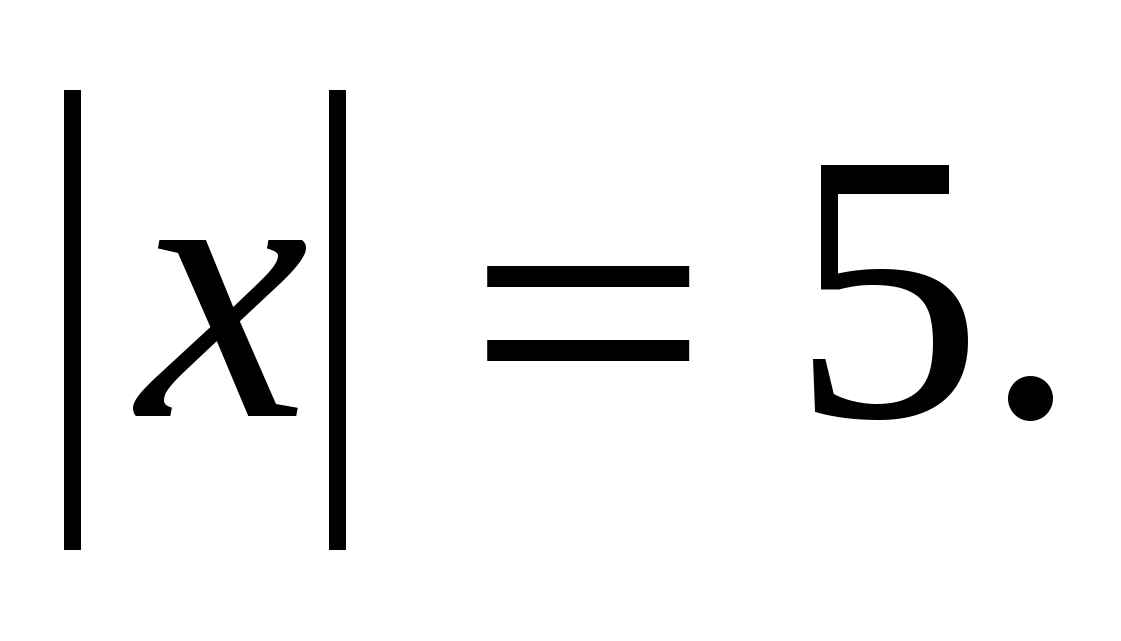
|
1) 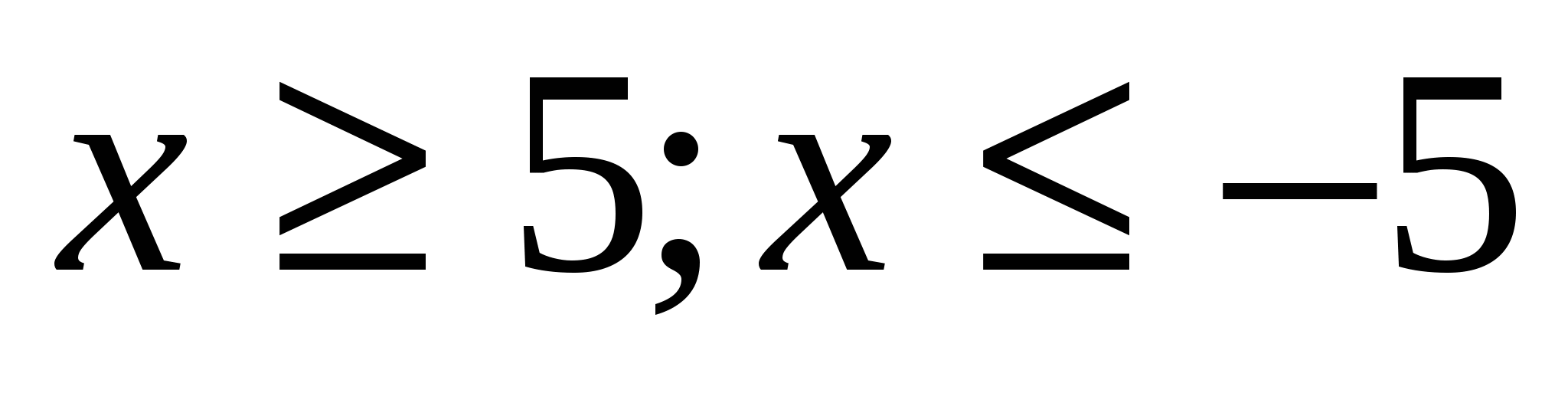
|
2)  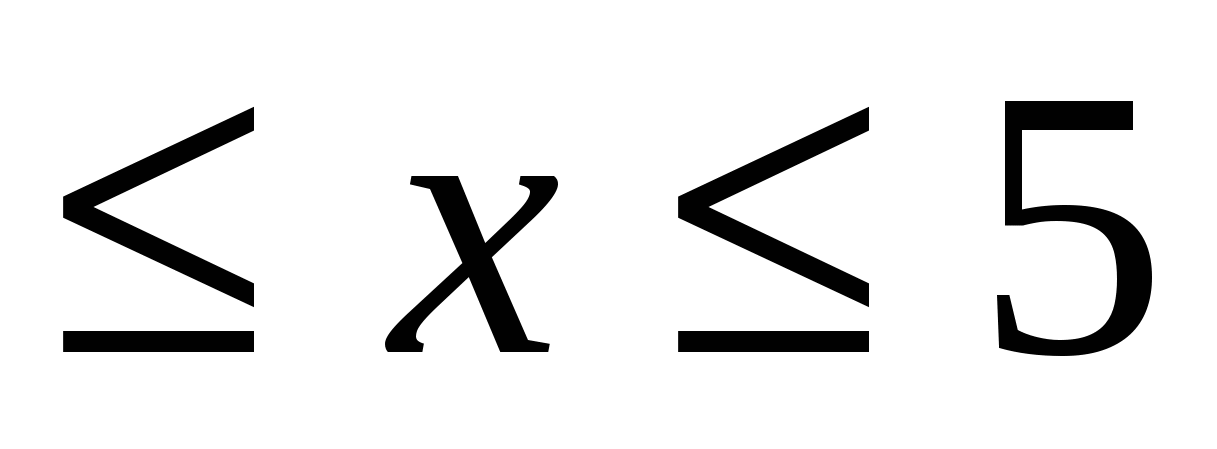
|
3) x =5
|
4) x  = = 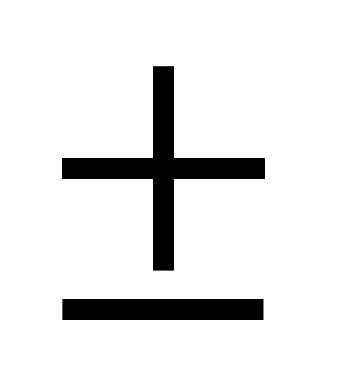 5 5
|
12
|
Решить уравнение 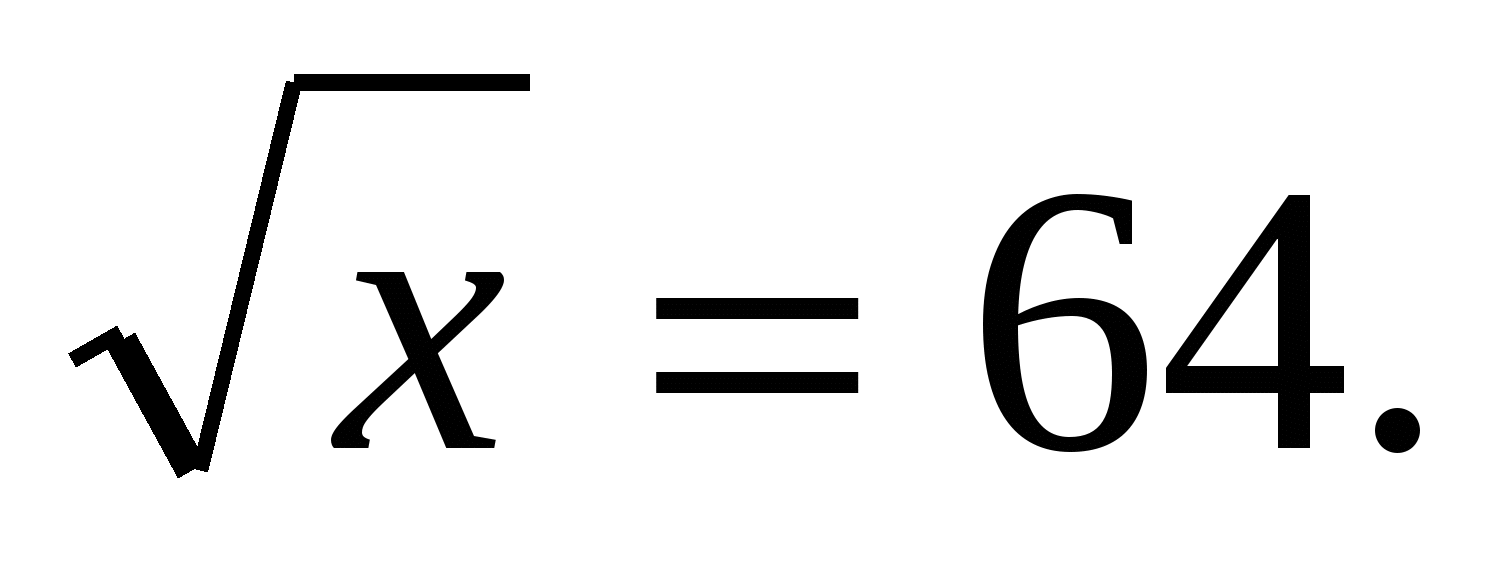
|
1) x = 32
|
2) x = 16
|
3) x = 8
|
4) x = 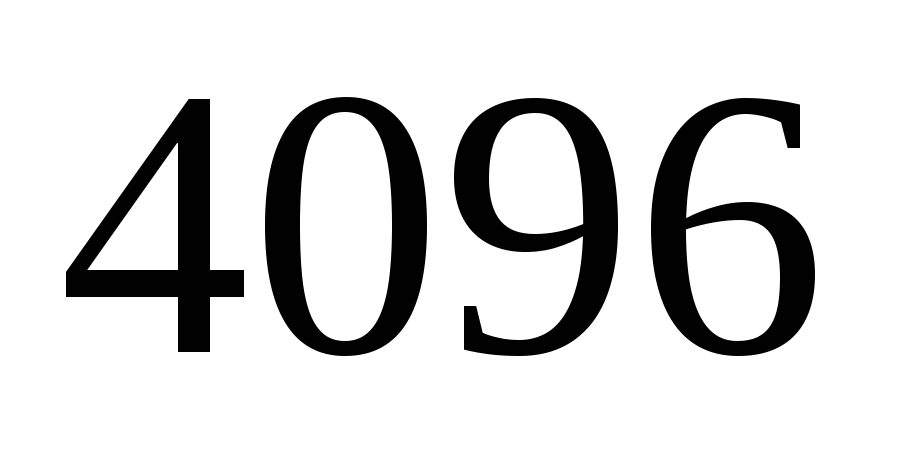
|
13
|
Вычислить 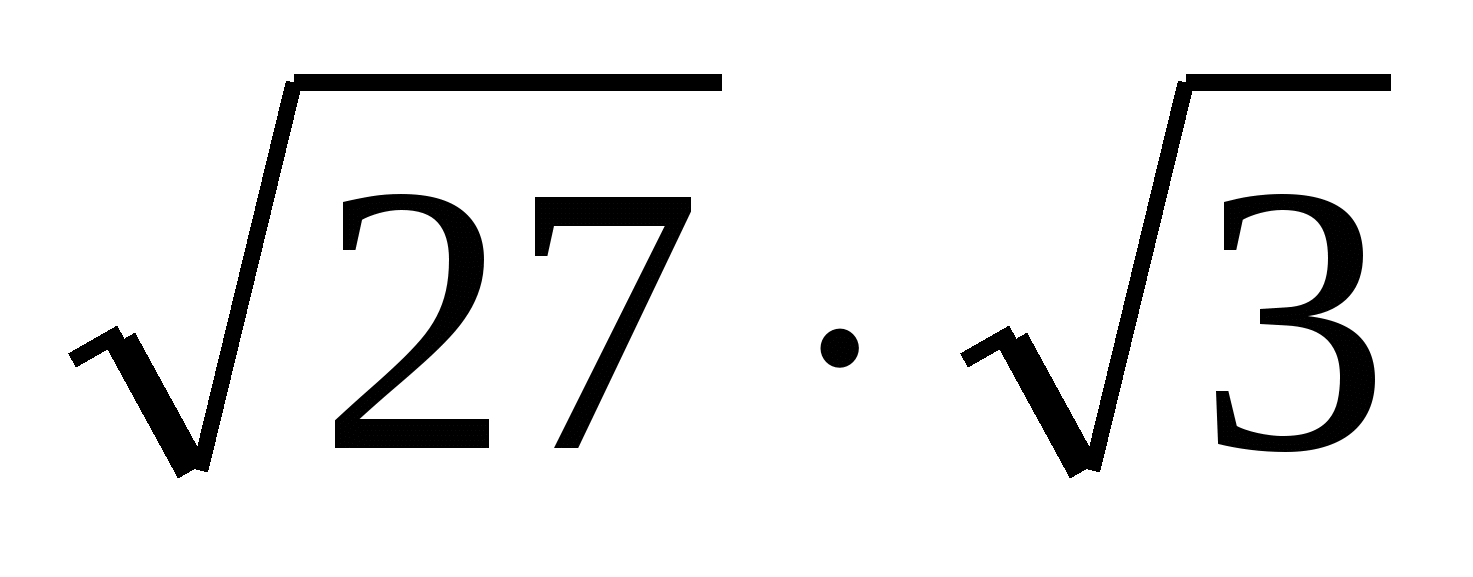 . .
|
1) 3
|
2) 27
|
3) 9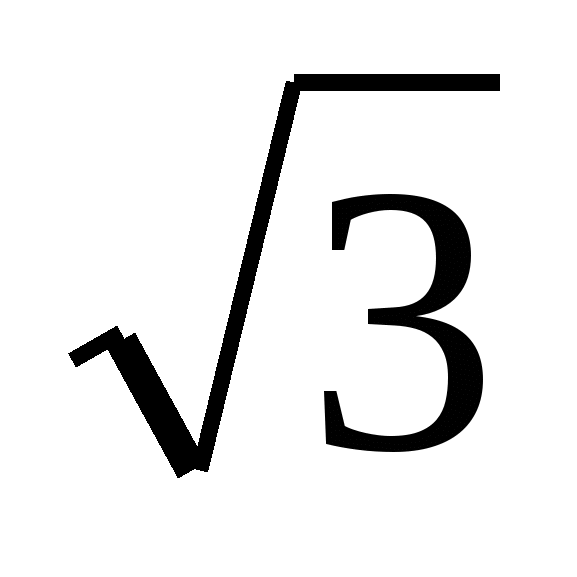
|
4) 9
|
14
|
Вычислить 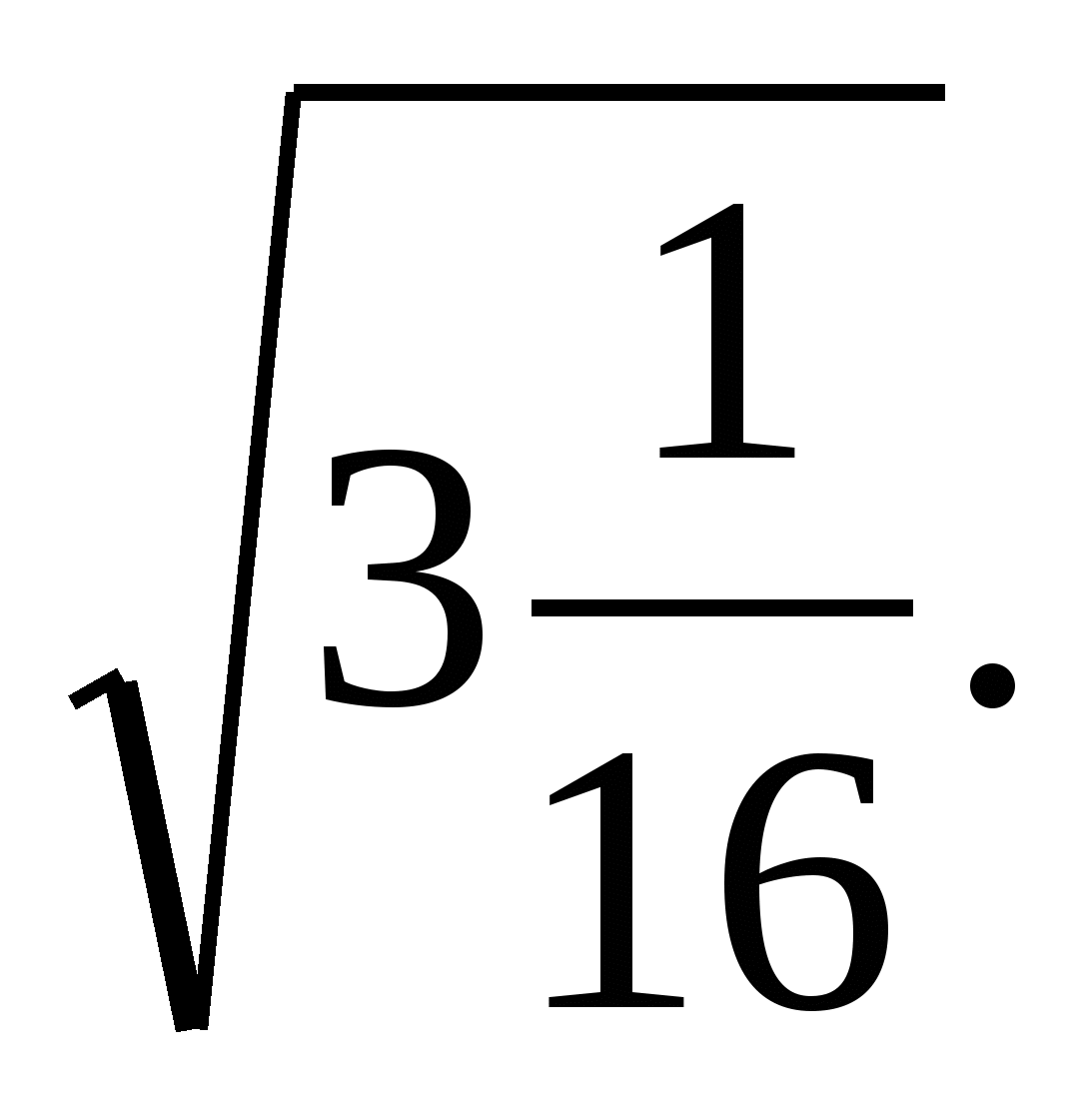
|
1) 1,75
|
2) 3,25
|
3) 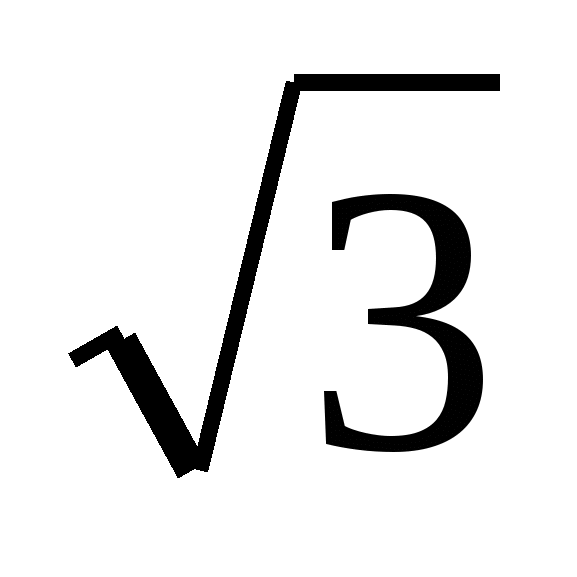 + 0,25 + 0,25
|
4) 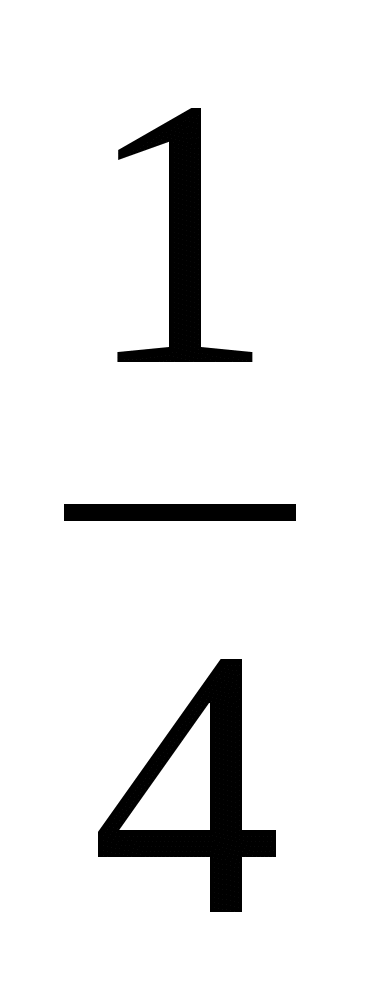 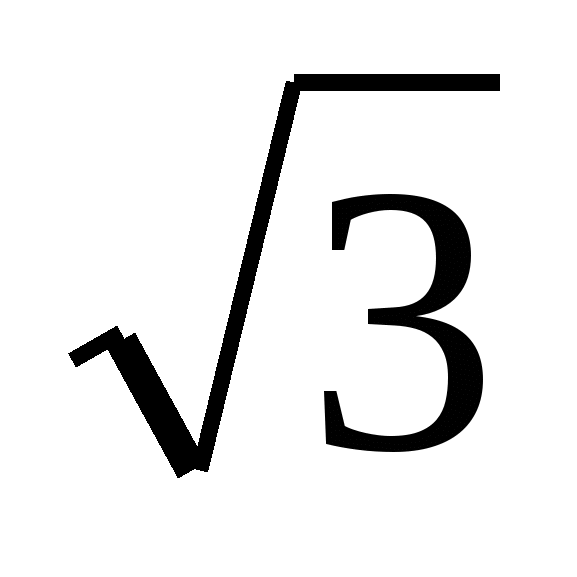
|
15
|
Вынести множитель из-под знака корня 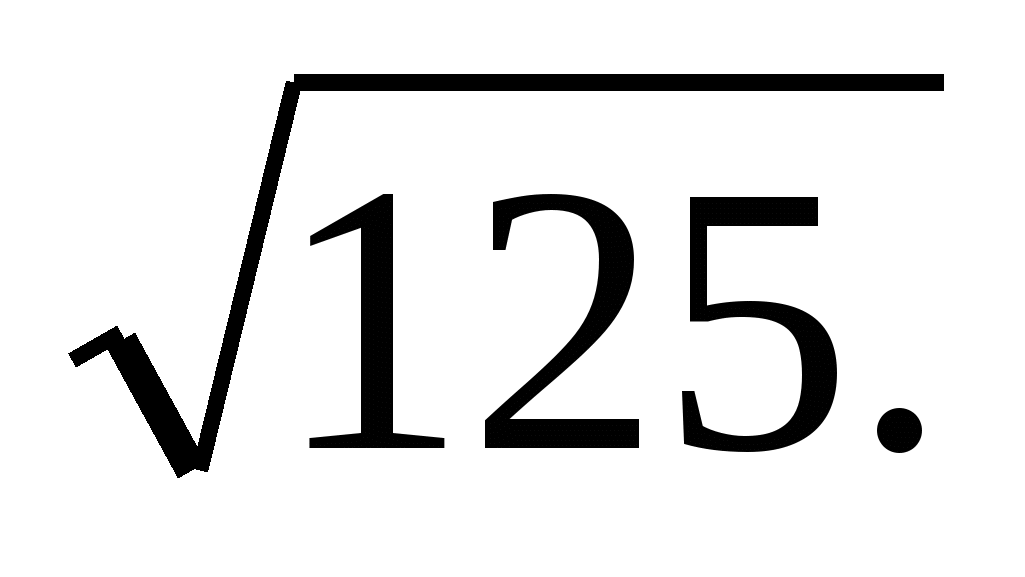
|
1) 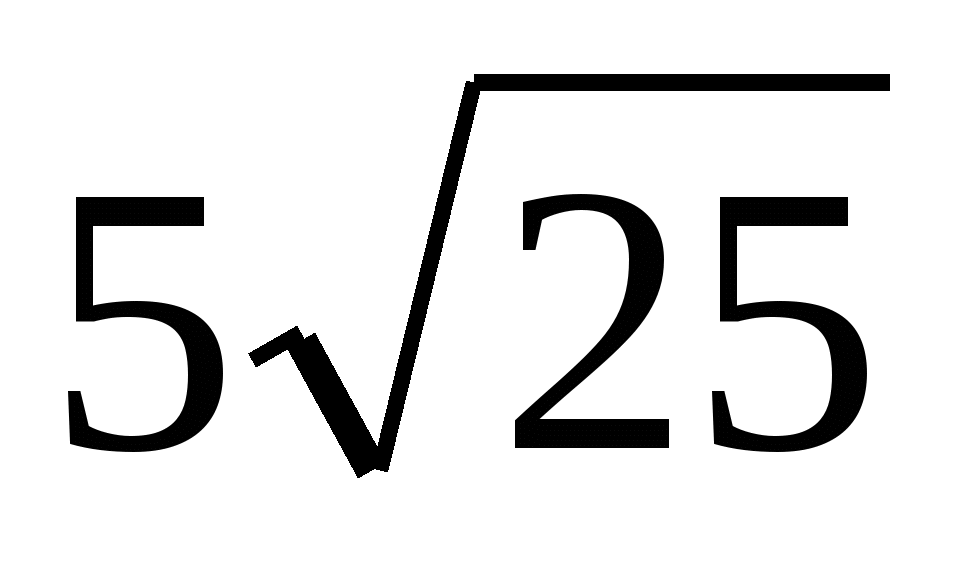
|
2) 25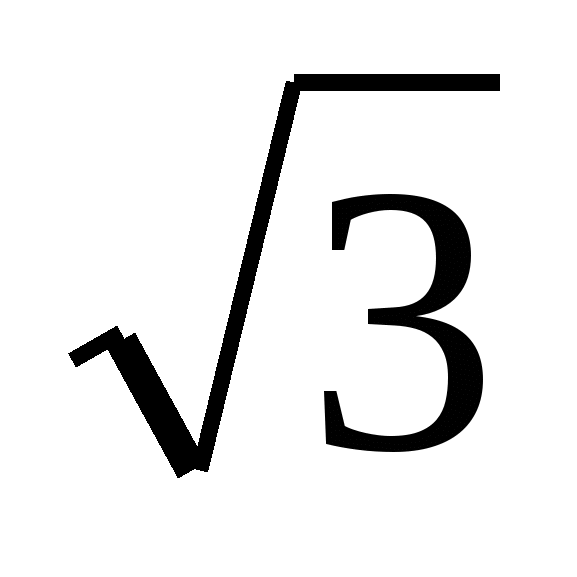
|
3) 5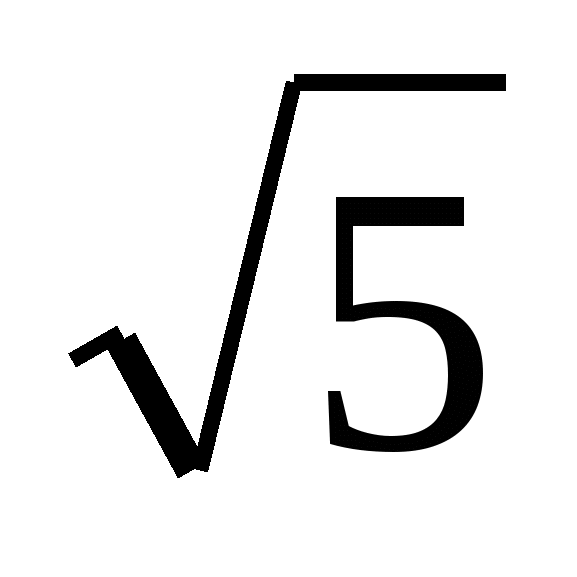
|
4) 5
|
16
|
Внести множитель под знак корня -2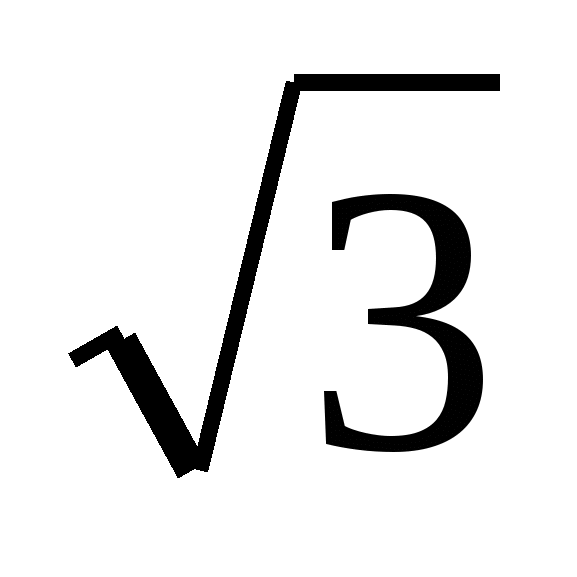 . .
|
1) 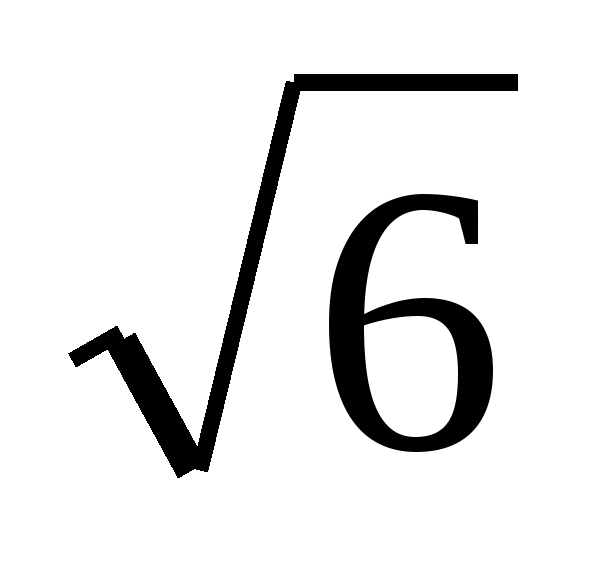
|
2) -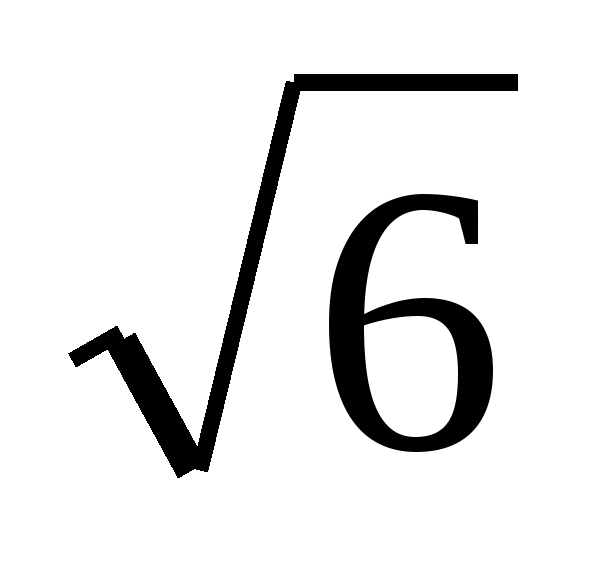
|
3) 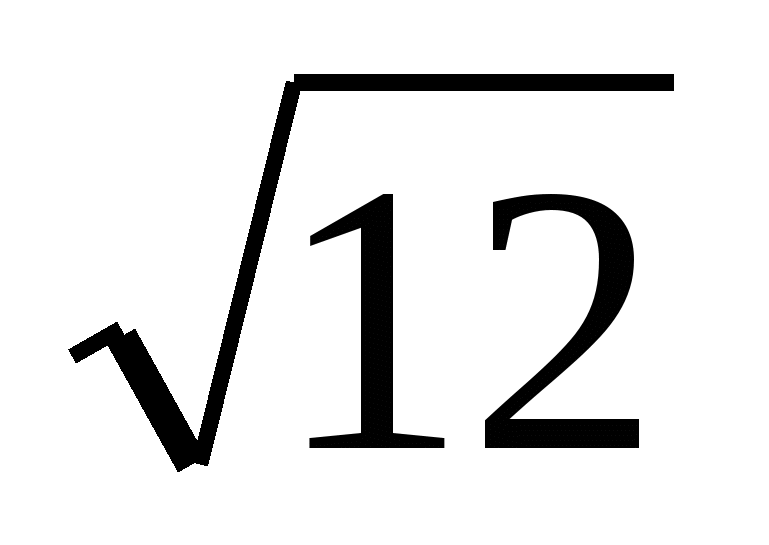
|
4) -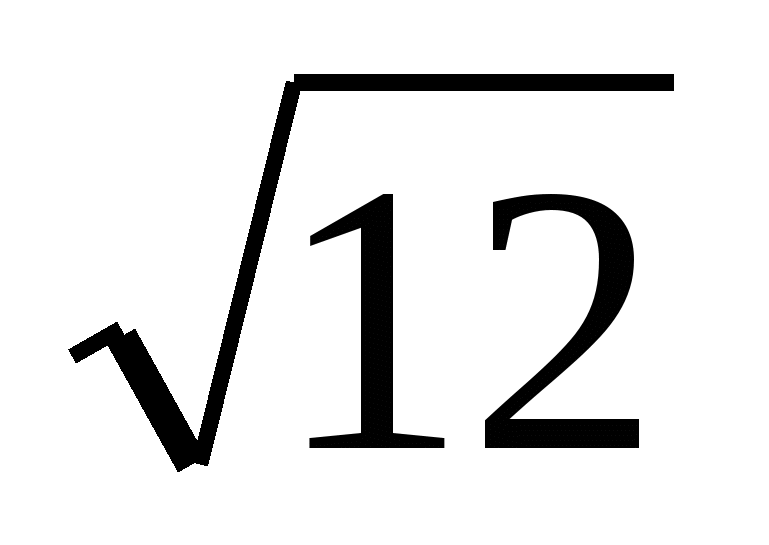
|
17
|
Решить уравнение x2 = 64
|
1) 8
|
2) 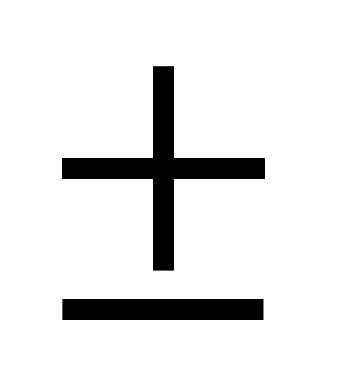 8 8
|
3) 32
|
4) 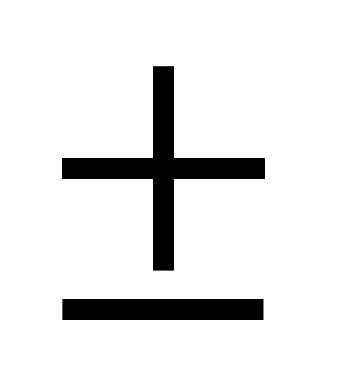 32 32
|
18
|
Найти корни уравнения x2 + x = 0.
|
1) 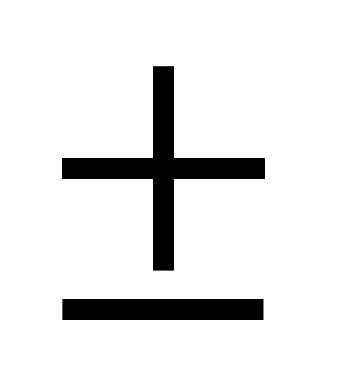 1; 0 1; 0
|
2) 1; 0
|
3) –1; 0
|
4) 0
|
19
|
Решить уравнение 3x2 + 8x – 3 = 0
|
1) 3; 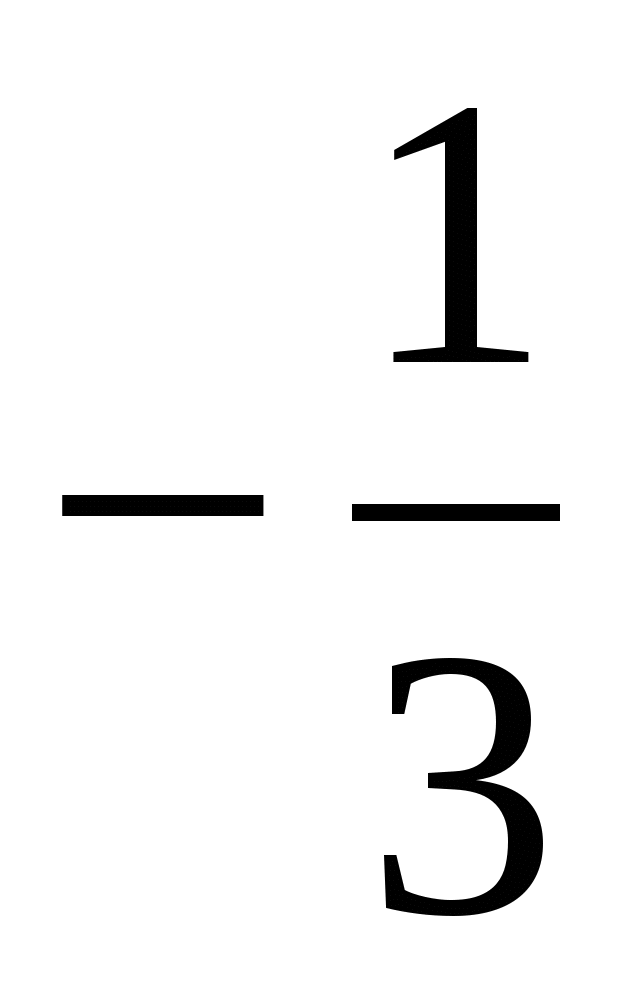
|
1) -3; 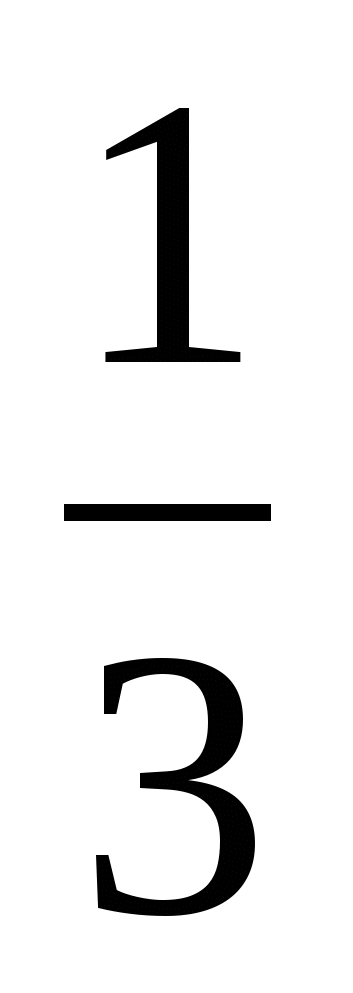
|
3) 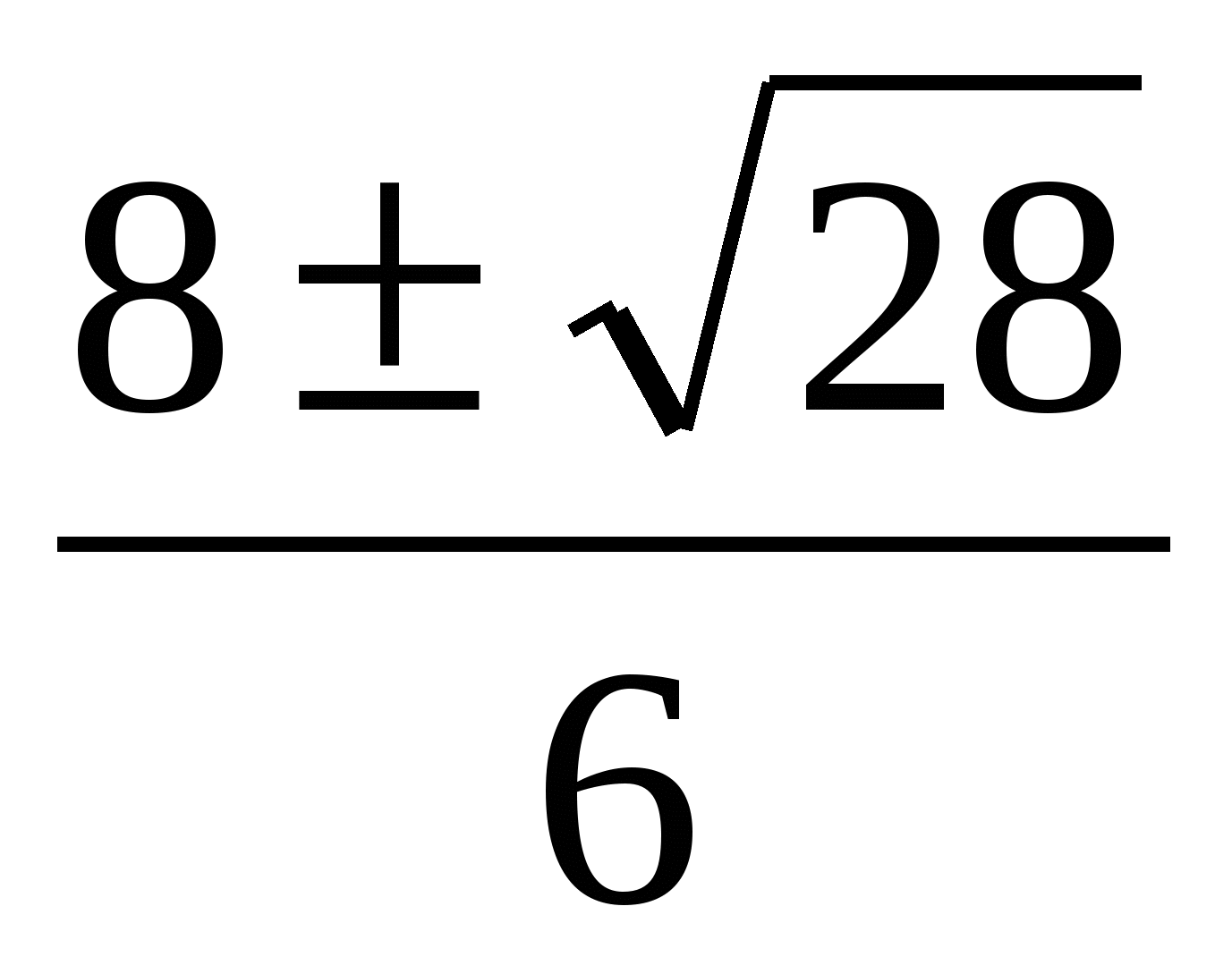
|
4) нет корней
|
20
|
По теореме Виета найти произведение корней приведенного квадратного уравнения
x2 – 5x + 3 = 0.
|
1) -3
|
2) 5
|
3) -5
|
4) 3
|
Часть 2. Записать решение.
Доказать, что для любых неотрицательных x справедливо неравенство 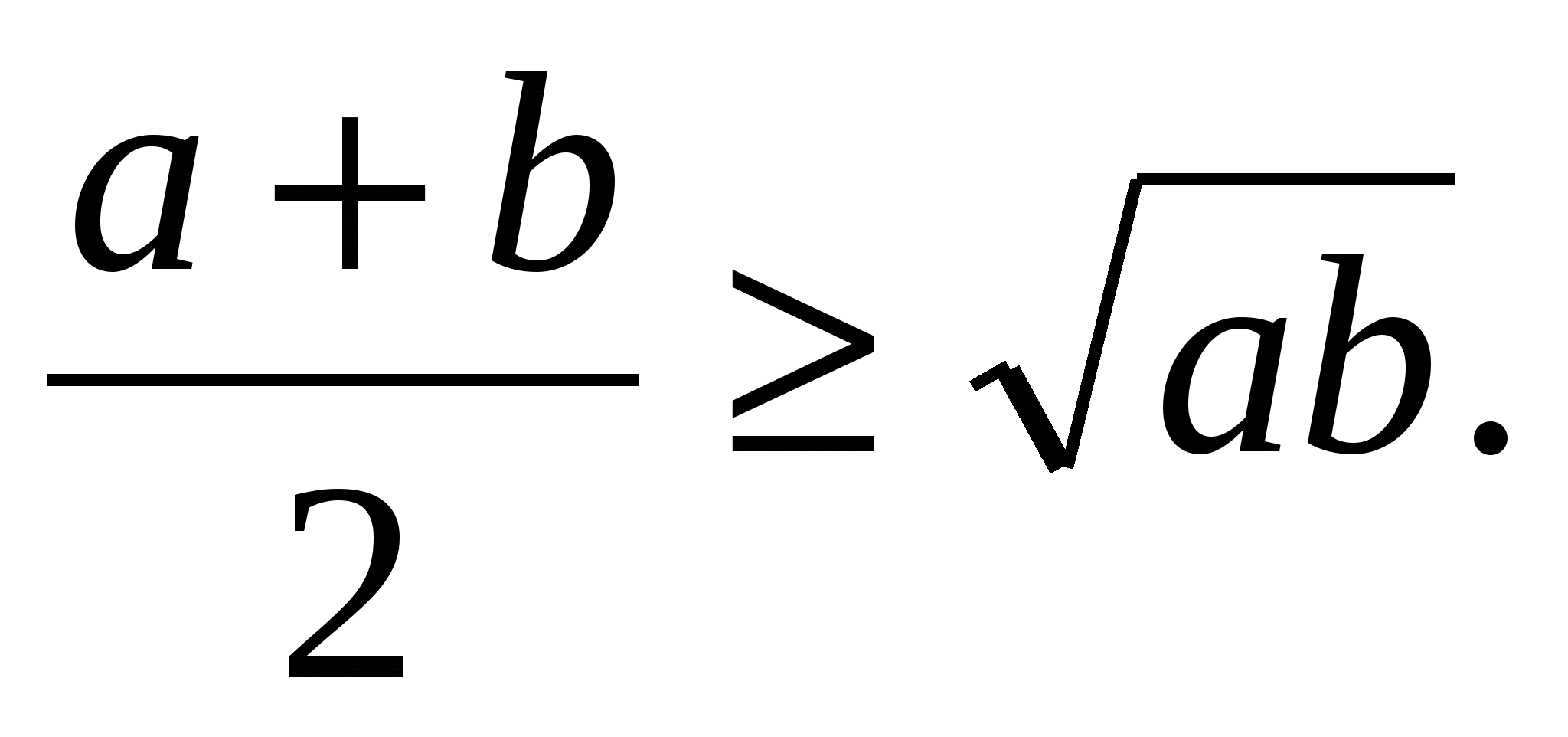
Вычислить 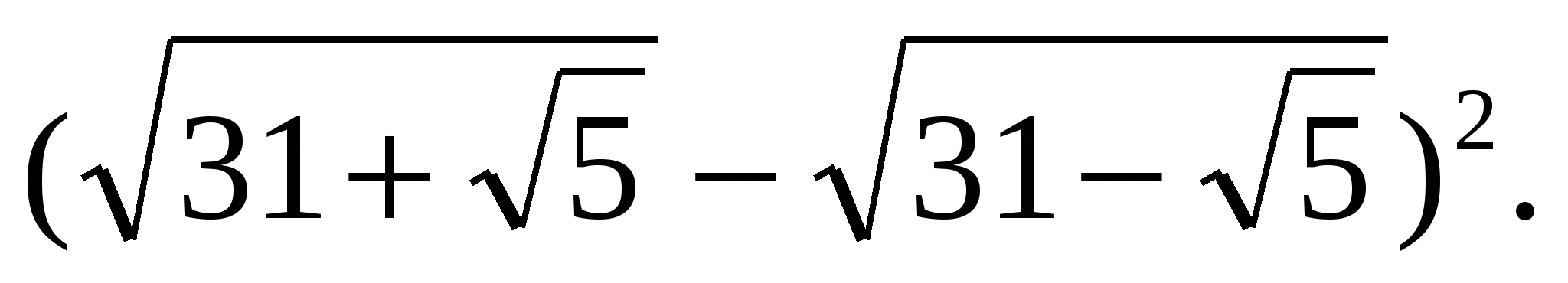
Решить уравнение 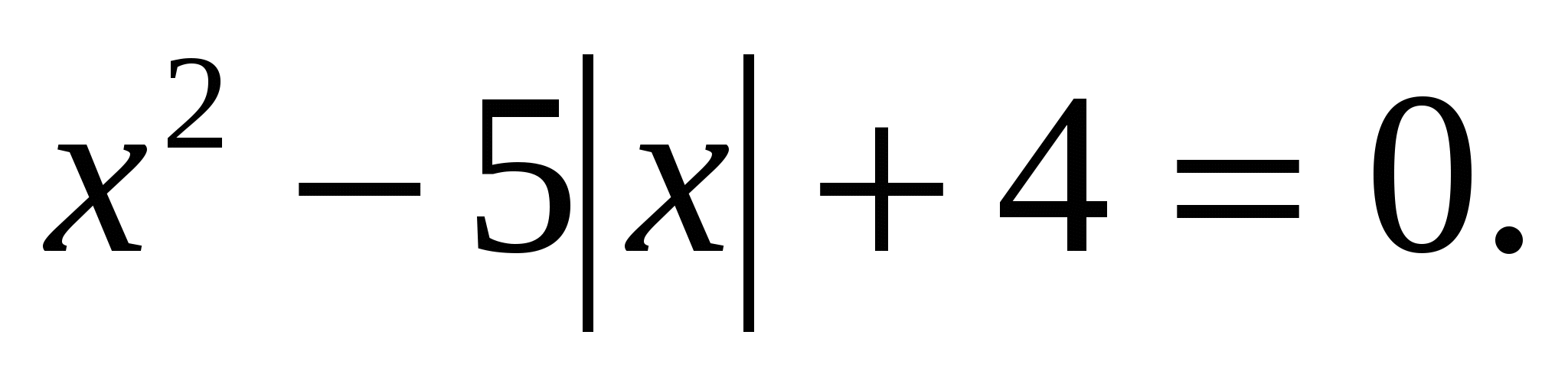
Планирование содержания обучения по темам
Рациональные дроби и их свойства
Компетенции:
Формирование умения производить действия с алгебраическими дробями.
Усвоение способов решения текстовых задач с помощью дробно –рациональных уравнений.
| |
|
|
 Скачать 465.77 Kb.
Скачать 465.77 Kb.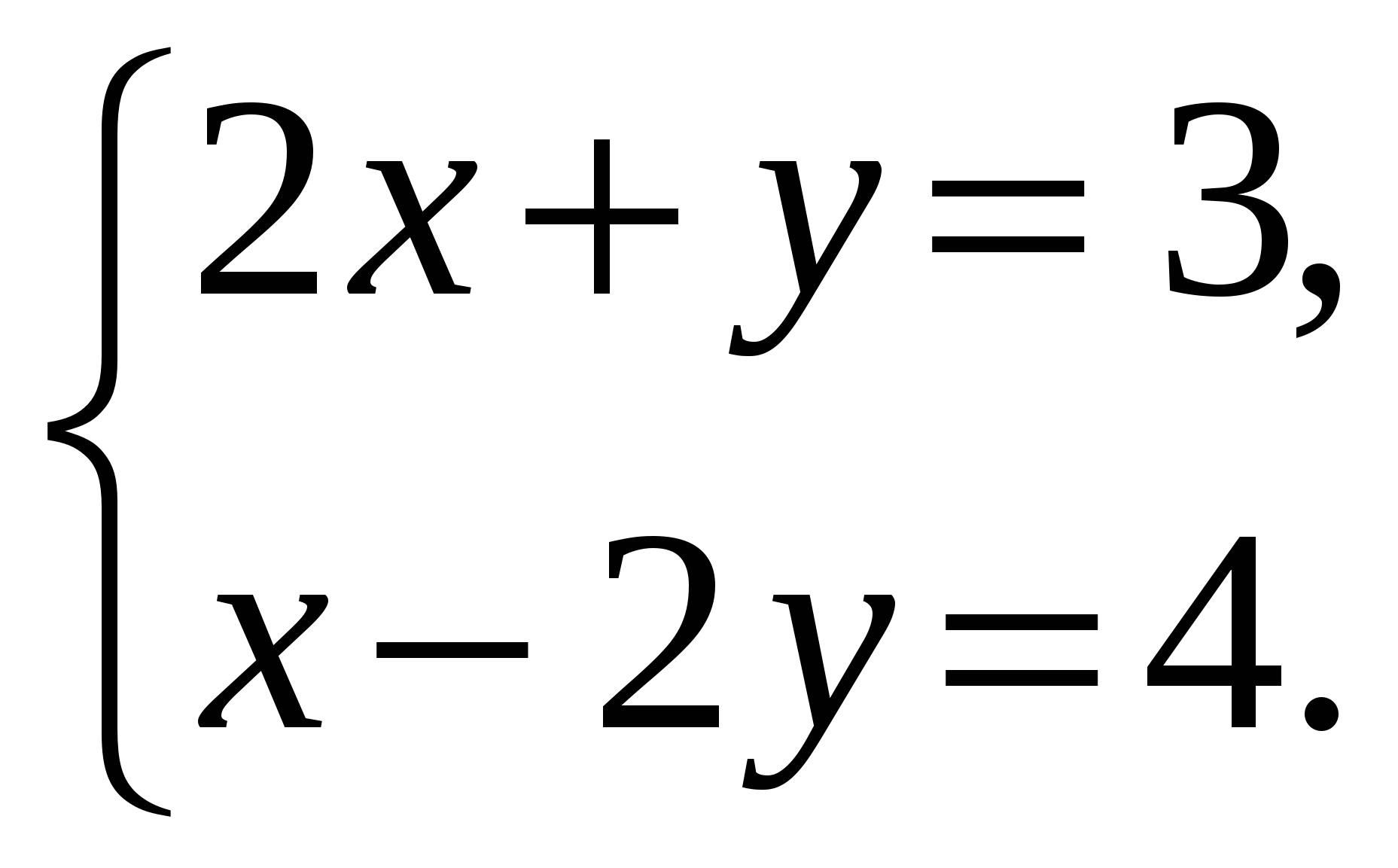
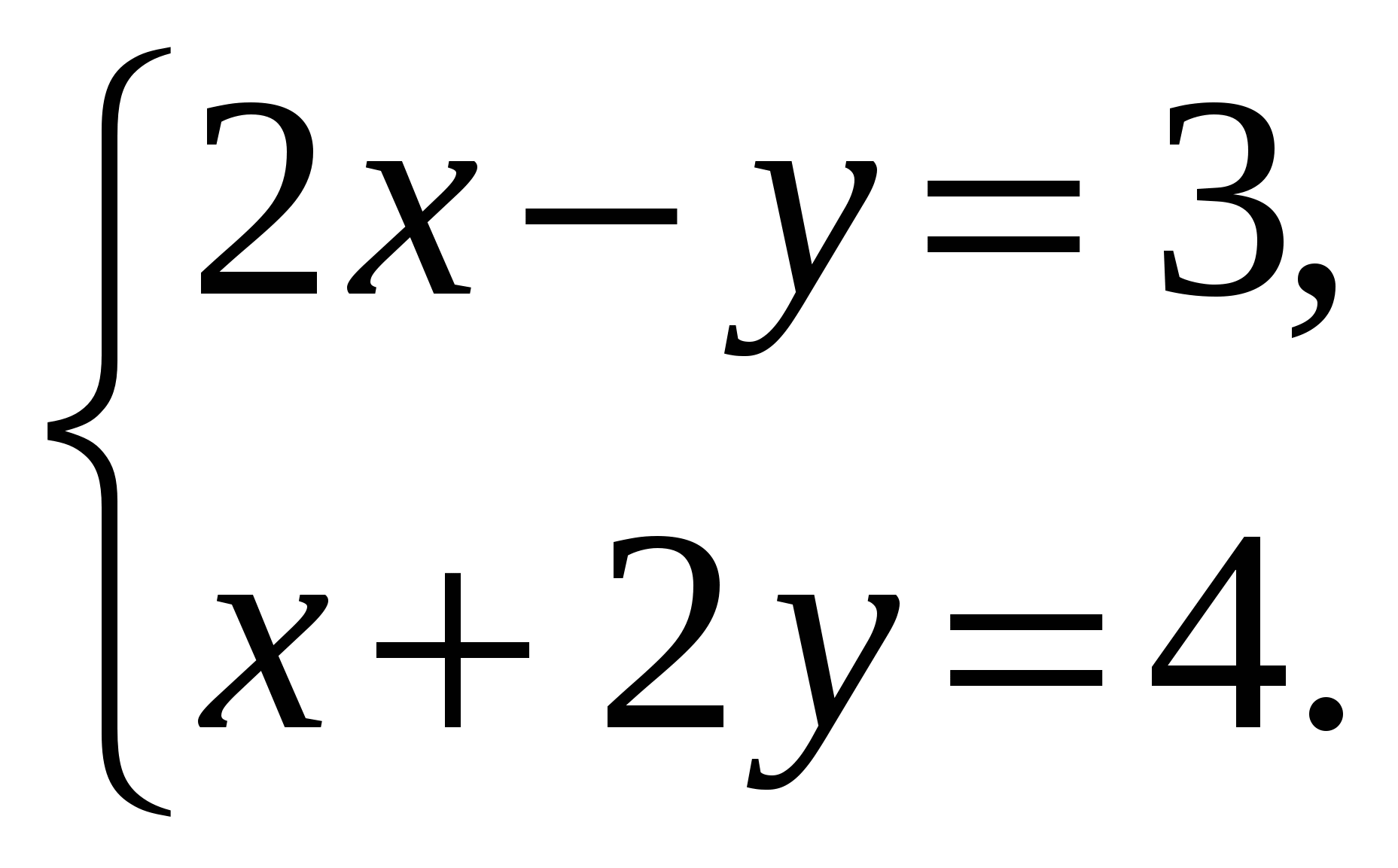
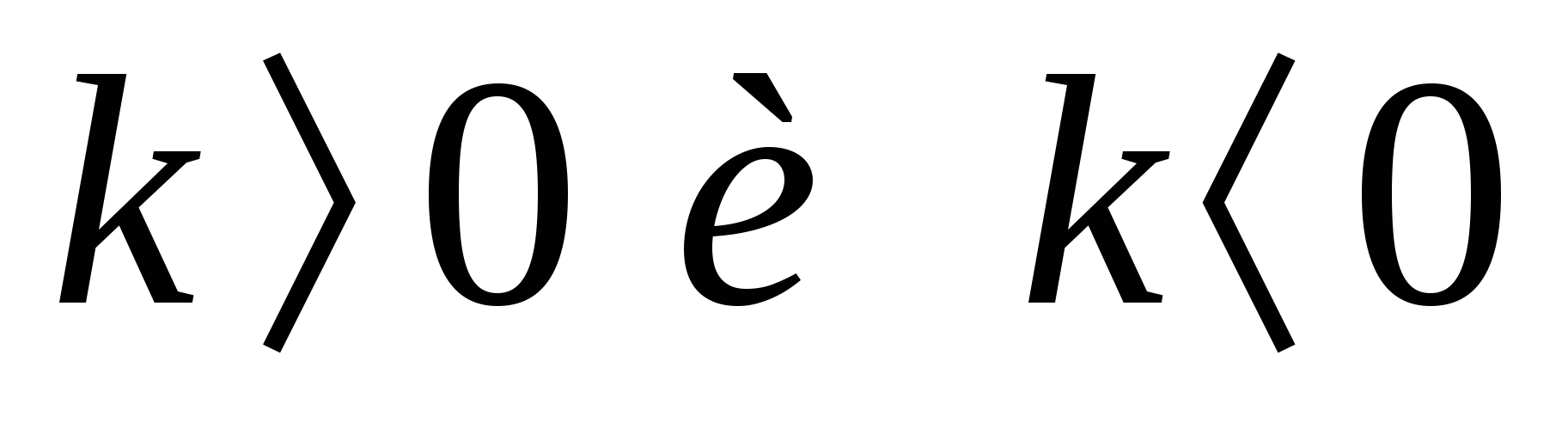 ?
?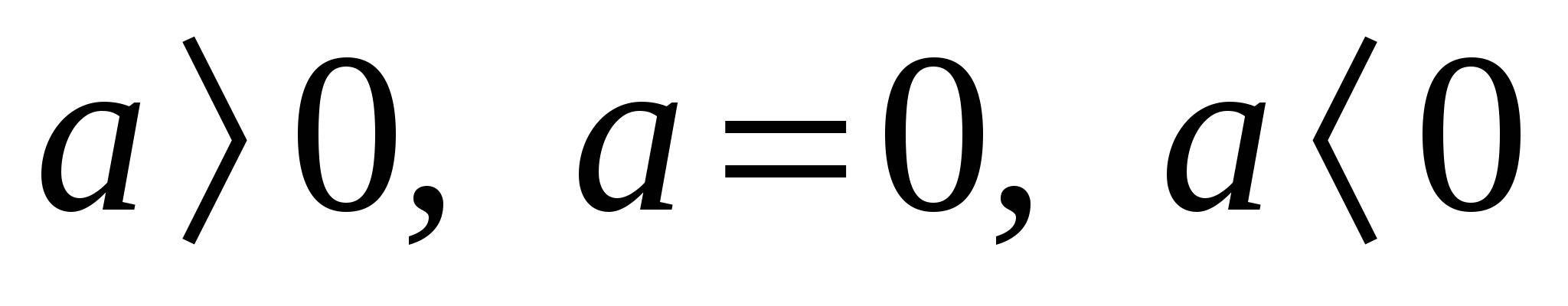 и если имеет, то сколько?
и если имеет, то сколько?