Урок лекция. Класс: 8 класс. Продолжительность урока: 45 минут. Учебник: А. Г. Мордкович и др. Алгебра 8
 Скачать 41.09 Kb.
|
| Тема: Теорема Виета. Тип урока: урок лекция. Класс: 8 класс. Продолжительность урока: 45 минут. Учебник: А.Г. Мордкович и др. Алгебра 8. Цели урока:
Ход урока: Все дома решили уравнения вида  . Получили корни:
Надо установить связь между  и  ;  ,и  .  .Прекрасно! Мы установили это из данных уравнений. Проверим гипотезу! а)  , ,  ,   .Гипотеза верна! б)      Уравнение имеет два равных корня. Гипотеза верна! в)   – 4 < 0, действительных корней нет.Значит, гипотеза неверна? Гипотезу надо уточнить! Если уравнение  имеет корни, то   Теперь эту гипотезу надо доказать! Открыл и доказал эту теорему французский ученый математик Франсуа Виет. Домашним заданием вам будет законспектировать доказательство этой теоремы одним из способов из учебника и поискать материал о жизни и деятельности Ф. Виета. В классе докажем ее другим способом. Пусть  и  – корни квадратного уравнения . Надо получить: Что значит и корни уравнения? (1) (2)Вычтем из (1) уравнения (2), получим:      или  докажем этот случай на консультации  Подставим найденной значение для в (1) уравнение:    Получили: Мы открыли, потом доказали теорему Виета. Верна и обратная теорема. Дано:  – числа,  Доказать: – корни уравнения .Доказательство:      0 = 0 (верно) 0 = 0 (верно)  – корень  – корень.ч.т.д. Где использовать теорему Виета? 1). Можно, не находя корни, найти сумму и произведение корней квадратного уравнения вида 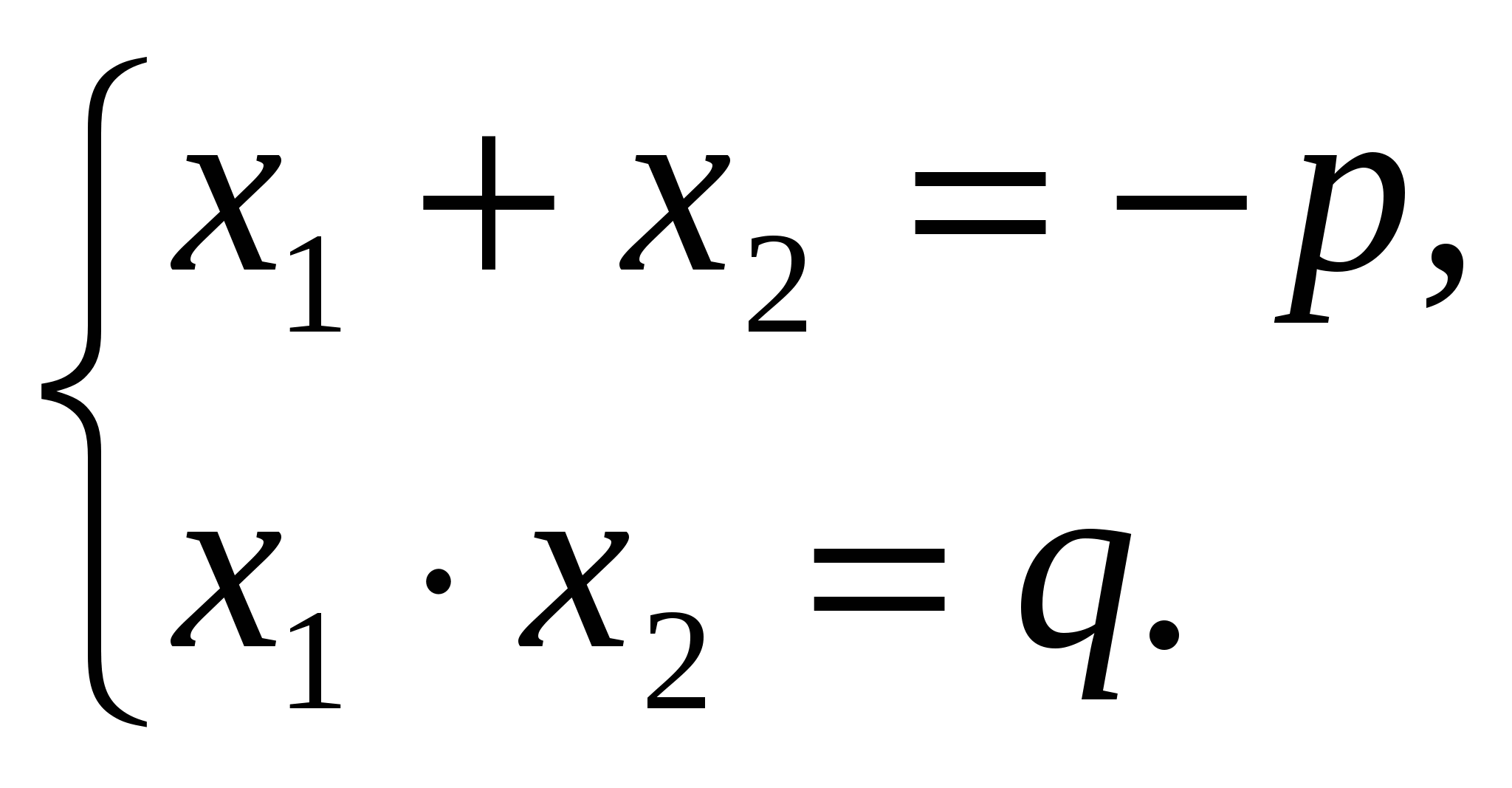:  2). Не решая уравнение  , найти   Итак,  Где использовать теорему, обратную теореме Виета? а). Можно проверить правильность решения квадратного уравнения.     Покажем, что корни уравнения найдены правильно:   – 8 + 5 = – 3. – 8 5 = – 40. Значит, по теореме, обратной теореме Виета, числа – 8 и 5 являются корнями уравнения  б). Найти подбором корни квадратного уравнения (устно):     Как быть, если уравнение имеет вид  где  Стихотворение «Теорема Виета», поэт Александр Гуревич: По праву достойна в стихах быть воспета О свойствах корней теорема Виета. Что лучше, скажи, постоянства такого: Умножишь ты корни – и дробь уж готова: В числителе  , в знаменателе  А сумма корней тоже дроби равна. Хоть с минусом дробь эта, что за беда – В числителе  , в знаменателе     Итак,     Итак, мы научились применять теорему Виета и обратную ей для уравнений вида и  Угадайте корни уравнений:   Что трудно? Тогда решите сначала три таких уравнения, найдя корни подбором.        Что вы заметили? (Один из корней равен 1). Установите связь между  и корнями. Если  , тогда один из корней 1, а другой  .Теорему Виета применяют для решения квадратных уравнений, где или  . Это дает значительное преимущество для быстрого получения ответа.Если в уравнении  , то один из его корней 1, а другой .Если в уравнении , то один из его корней – 1, а другой  Теперь вернитесь к решению уравнений Придумайте дома по 3 красивых уравнения и предложите решить их товарищу. |
