Пояснительная записка
 Скачать 69.98 Kb. Скачать 69.98 Kb.
|
                                        Пояснительная записка. Пояснительная записка.Материал, связанный с неравенствами, составляет значительную часть школьного курса математики. Это объясняется тем, что неравенства широко используются в различных разделах математики, в решении важных прикладных задач. Неравенства сами по себе представляют интерес для изучения, так как именно с их помощью на символическом языке записываются важнейшие задачи познания реальной действительности. Как в самой математики, так и в ее приложениях с неравенствами приходится сталкиваться не менее часто, чем с уравнениями. Неравенства являются наиболее компактным, легко обозреваемым и доступным для учащихся материалом, на котором отрабатываются сложнейшие математические методы. Изучение программного материала дает возможность учащимся:
Система заданий ЕГЭ всегда содержит неравенства в прямом или косвенном виде. Тема. Решение логарифмических и показательных неравенств. Цель: добиться более глубокого усвоения знаний, высокого уровня обобщения и систематизации. Задачи. Образовательная: -выявить качество и уровень усвоения ЗУ, полученными на предыдущих уроках по данной теме; обобщить материал как систему знаний. Воспитательная: воспитывать общую культуру, создать условия для реальной самооценки учащихся. Развивающая: развивать умение классифицировать, выявлять связи, формулировать выводы, развивать коммуникативные навыки при работе в группах, развивать познавательный интерес. Тип. Урок повторения, систематизации и обобщения знаний, закрепления умений. Учебник: С. М. Никольский. Алгебра и начало математического анализа. Базовый. Форма: повторительно-обобщающий урок. Методы: словесный, исследовательский. Средства: доска, ИД, проектор. Приемы: классификация. Формы деятельности: групповая. Ход урока.
- Сегодня на уроке мы продолжим отрабатывать навыки решения неравенств показательных, логарифмических и комбинированных. III. Проверка домашнего задания. - Дома вам было предложено решить неравенства, применяя наиболее рациональные методы, в том числе: метод интервалов, использование областей определения функции, использование неотрицательности функций, использование ограниченности функций. Кроме этого вы должны были подготовить по группам теоретическую справку о методах решения неравенств и привести примеры решения неравенств. 1 группа. Метод равносильных преобразований (презентация) 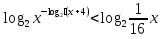 Решение. Пролагорифмируем обе части по основанию 2. (4 – log2x)( log2x)<- 4 + log2x Пусть log2x=t, где х >0, тогда (4 – t)t<-4+t (t – 4)(t + 1) >0 4 Cделав обратную замену получим (0;0,5) 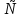 (16; (16;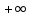 ) )Ответ: (0;0,5) 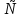 (16; (16;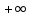 ) )2 группа. Метод интервалов (презентация) 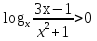 Решение. Ограничения 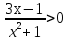 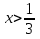 x>0, x 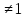 x>0, x x>0, x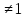 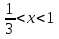 х > 1 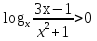 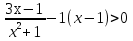 (х – 1)2(х – 2)< 0 (х – 1)2(х – 2)< 0 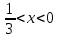 x > 1 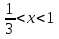 x < 1 1< x < 2 1< x < 2 Ответ: ( 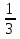 ; 1) ; 1)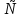 (1;2). (1;2).3 группа. Использование ограниченности функций (презентация) lg (х2 +2х + 2) +5 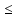 4 – 2х – х2 4 – 2х – х2Решение. Обе части неравенства определены для х 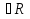 . Преобразуем обе части неравенства lg (х2 +2х + 2) = lg ((х2 +2х + 1) + 1) = lg((х + 1)2 + 1) . Преобразуем обе части неравенства lg (х2 +2х + 2) = lg ((х2 +2х + 1) + 1) = lg((х + 1)2 + 1)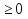 , тогда lg((х + 1)2 + 1) , тогда lg((х + 1)2 + 1)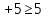 4 – 2х – х2 = - (х2 + 2х + 1) +5 = 5 – (х + 1)2 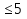 Следовательно, lg (х2 +2х + 2) +5=5 4 – 2х – х2 = 5 lg (х2 +2х + 2) = 1 (х + 1)2 = 0 х2 +2х + 2 = 1 х = - 1 (х + 1)2 = 0 х = - 1 х = - 1 Ответ: – 1. 4 группа. Использование неотрицательности функций (презентация)  Решение. (3х)2 – 2 · 3х ·2х + 2(2х)2 – 2 · 2х +1> 0 (3х – 2х)2 + (2х – 1) > 0 Каждая из функций f1(х) = (3х – 2х)2 и f2(х) = (2х – 1) неотрицательна для любого х 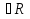 ? Поэтому это неравенство равносильно системе ? Поэтому это неравенство равносильно системе3х – 2х =0 3х = 2х 2х – 1 = 0 2х = 1 х=0 Ответ: 0.
- Сейчас вам будет предложено четыре неравенства, вы в группах должны будете обсудить методы их решения, решить и защитить свое решение. 1. 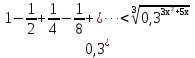 Решение. Данное неравенство можно назвать комбинированным. Преобразуем показатели степеней. Рассмотрим (bn): 1; - 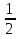 ; ; 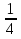 ; ; 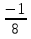 ; …. q = ; …. q =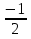 (бесконечно убывающая геометрическая прогрессия) (бесконечно убывающая геометрическая прогрессия)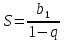 ; ; 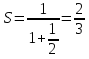 Получим: 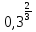 = = 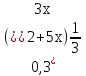 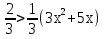 2 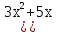 ) 3х2 +5х – 2 < 0 - 2< x < ) 3х2 +5х – 2 < 0 - 2< x < 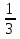 Ответ: (-2; 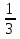 ) )2. 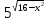 + 3 + 3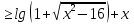 Решение. Найдем область существования функций. По определению арифметического квадратного корня 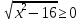 , поэтому достаточно найти решение системы: , поэтому достаточно найти решение системы:16 – х2 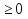 х2 – 16 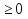 х2 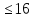 х2 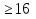  х 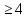 х 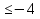 х= - 4 х = 4 Проверка: х = - 4, 50 + 3 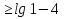 4 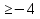 – верно – верно х = 4, 50 + 3 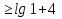 4 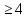 - верно - верноОтвет: - 4; 4. 3. 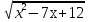 + lg2(х2 – 4х +1) + lg2(х2 – 4х +1)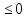 Решение: f1(х) = 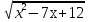 , f1(х) , f1(х)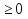 на D (f1) на D (f1)f2(x) = lg2(х2 – 4х +1), f2(x) 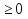 на D (f2) на D (f2)Поэтому 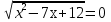 lg2(х2 – 4х +1) = 0 х2 – 7х + 12 = 0 х2 – 4х +1 = 1 х = 3 х = 4 х = 0 х = 4 х = 4 Ответ: 4.
Решение. Обе части уравнения определены для всех х 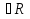 . .2х + 2-х 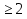 2  2х + 2-х = 2 2 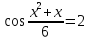 Единственное решение первого уравнения х = 0 удовлетворяет и второму уравнению системы. Значит, неравенство имеет единственное решение при х = 0. Ответ: 0.
- Какие существуют методы решения логарифмических и показательных неравенств? VI. Домашнее задание. Решить неравенства: а) 25х – 5 · 10х + 29 · 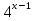 - 4 · - 4 ·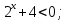 б) log4х +1 7+ log9х7 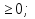 в) 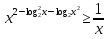 ; ;г) (4х2 + 2х +1 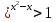 . . |
 .
.