Конспект урока по алгебре и началам анализа в 11 классе по теме «Решение трансцендентных уравнений»

Скачать 39.73 Kb. Название Конспект урока по алгебре и началам анализа в 11 классе по теме «Решение трансцендентных уравнений» Медвеженкова М.В Дата 05.03.2016 Размер 39.73 Kb. Тип Конспект

Государственное бюджетное нетиповое общеобразовательное учреждение Республики Мордовия «РЕСПУБЛИКАНСКИЙ ЛИЦЕЙ — ЦЕНТР ДЛЯ ОДАРЁННЫХ ДЕТЕЙ» Конспект урока по алгебре и началам анализа в 11 классе по теме «Решение трансцендентных уравнений» Разработала: преподаватель математики Медвеженкова М.В. Саранск 2013 Решение трансцендентных уравнений Не знаешь, с чего начать? Начни сначала. Льюис Керрол Тип урока: повторительно – обобщающий. Цели и задачи урока: Образовательные ­­- обобщение и углубление знаний учащихся об уравнениях и способах их решения. Подготовка к выпускным и вступительным экзаменам. Последовательный переход от одного уровня деятельности к следующему, более высокому, к новым знаниям, открытиям по этой теме. Развивающие – развитие умения работать с нетиповыми заданиями, формирование навыков самостоятельной работы с большим объемом информации; Воспитательные – воспитание самооценки, коммуникативных способностей. Формирование у учащихся понятий о научной организации труда, умений рецензирования ответов товарищей и корректированию собственных ответов. Оборудование: компьютер, мультимедийный проектор, доска. Ход урока. Организационный момент. Вступительное слово учителя Сообщение темы урока. Постановка целей и задач. Определение: Уравнения, содержащие логарифмическую, показательную или тригонометрическую функции, называются трансцендентными. Устный счет. Для актуализации опорных знаний проводится устная работа: 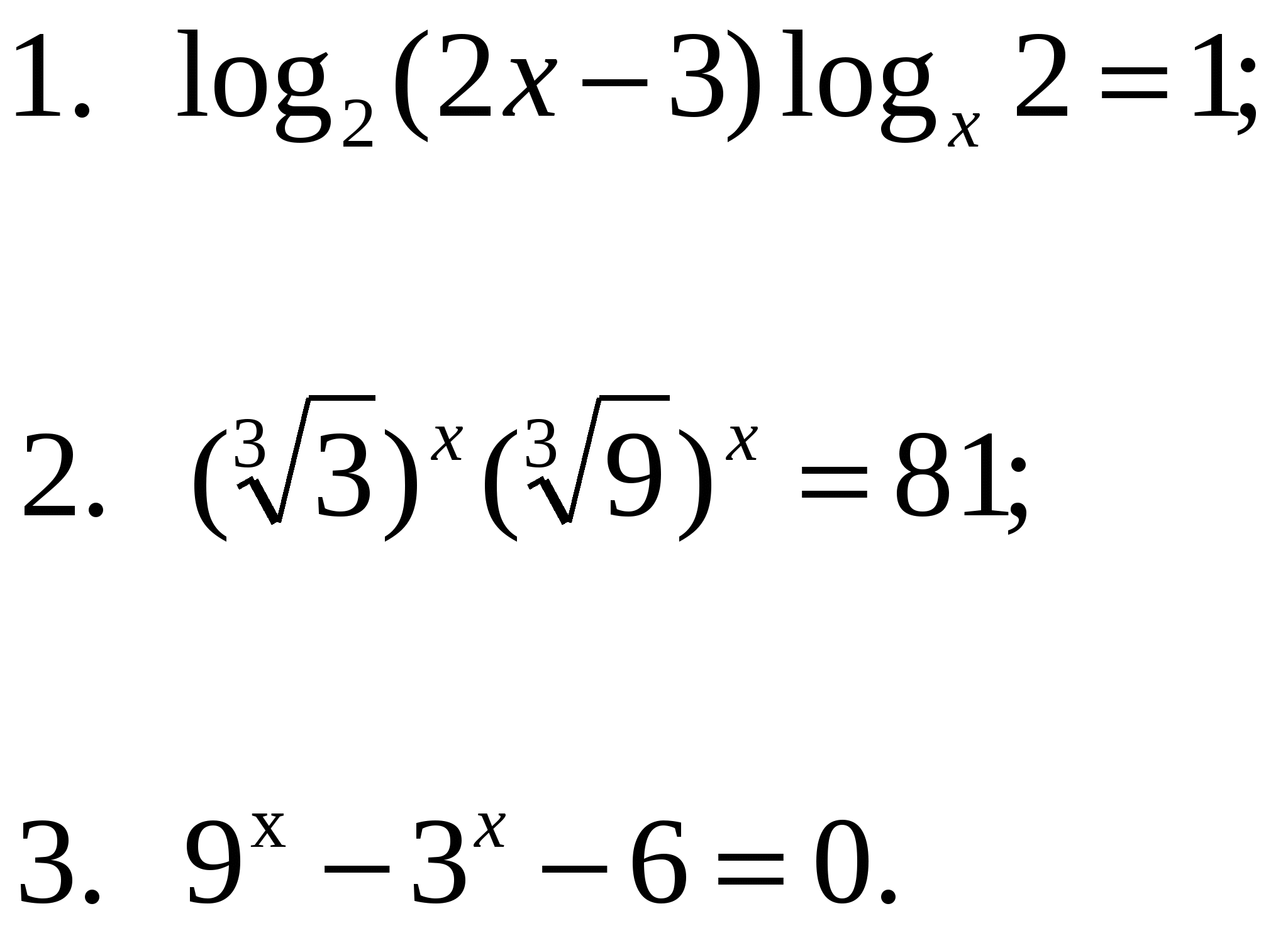Ответы: 1. х = 3; 2. х = 4; 3. х =1. 3. Решение уравнений. 3.1 Решение уравнений с применением монотонности функций. Если функция, стоящая в одной части уравнения, строго убывает, а функция, стоящая в другой части уравнения строго возрастает или константа, то уравнение имеет не более одного корня, который можно найти графически или подбором из ОДЗ Функция – возрастает, а функция – убывает. Значит, существует не более одного корня. Подстановкой убеждаемся, что х=1 – корень уравнения, и он единственный. Решить уравнение: Ответ: х= -1. 3.2. Уравнения с дополнительными условиями 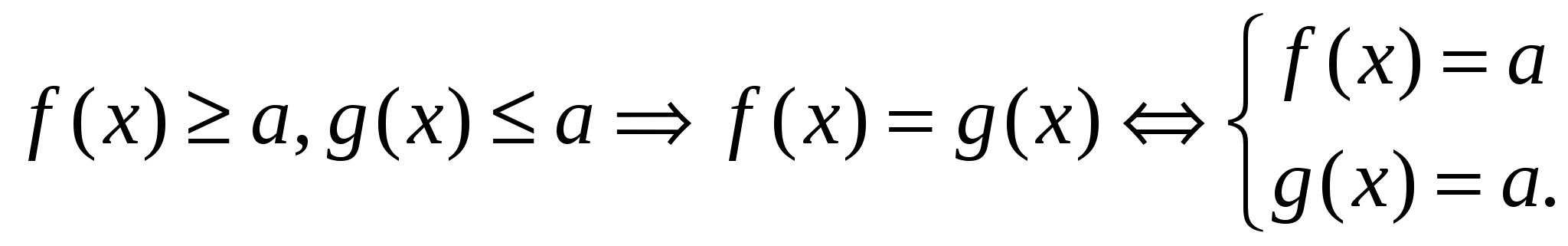Решение уравнений с применением оценки х = 0. х=0. 4. Самостоятельная работа. Самостоятельная работа проводится в виде теста. Всего 2 варианта, в каждом варианте 6 заданий. Вариант 1. а) Укажите, какому промежутку принадлежит корень уравнения 253-х = 0,2 1) (0, 1), 2) (1,2) 3) (2,3) 4) (3,4) б) Найдите произведение корней уравнения 3х -1 = 243 1) 6 2) -4 3)4 4) -6 в) Найдите сумму корней уравнения lg(4x-3) = 2lgx 1) -2 2) 4 3) -4 4)5 г) Сколько корней имеет уравнение = х2 – 3 1) 4 2) 2 3) 1 4) ни одного д) Решите уравнение = 1) 2) - 3) - 4) е) Решите уравнение 7+ х = 14 1) 21 2) 7 3) -7 4) 1 Вариант 2. а) Укажите, какому промежутку принадлежит корень уравнения log3(1-x) = 4 1) (62, 64), 2) (-81,-79) 3) (79,81) 4) (-12,-10) б) Сколько корней имеет уравнение = 1 – x2 1) 0 2) 1 3)2 4) 4 в) Найдите сумму корней уравнения log√3 x2 = log√3(9x-20) 1) 2 2) 4 3) -9 4)9 г) Укажите, какому промежутку принадлежит корень уравнения 4х-2 =0,51-х 1) (-4, -2) 2) (1,2) 3) (2,4) 4) (4,6) д) Решите уравнение х – 4 = 1) 5 2) - 1 3) 5 и -1 4) -5 е) Найдите наименьший корень уравнения 3∙9х - 5∙ 6х + 2∙ 4х = 0 1) -1 2) 0 3) 1 4) 2 Код правильных ответов: Задание а б в г д е 1 вариант 4 1 2 2 3 2 2 вариант 2 1 4 3 1 1 6. Подведение итогов урока. Домашнее задание.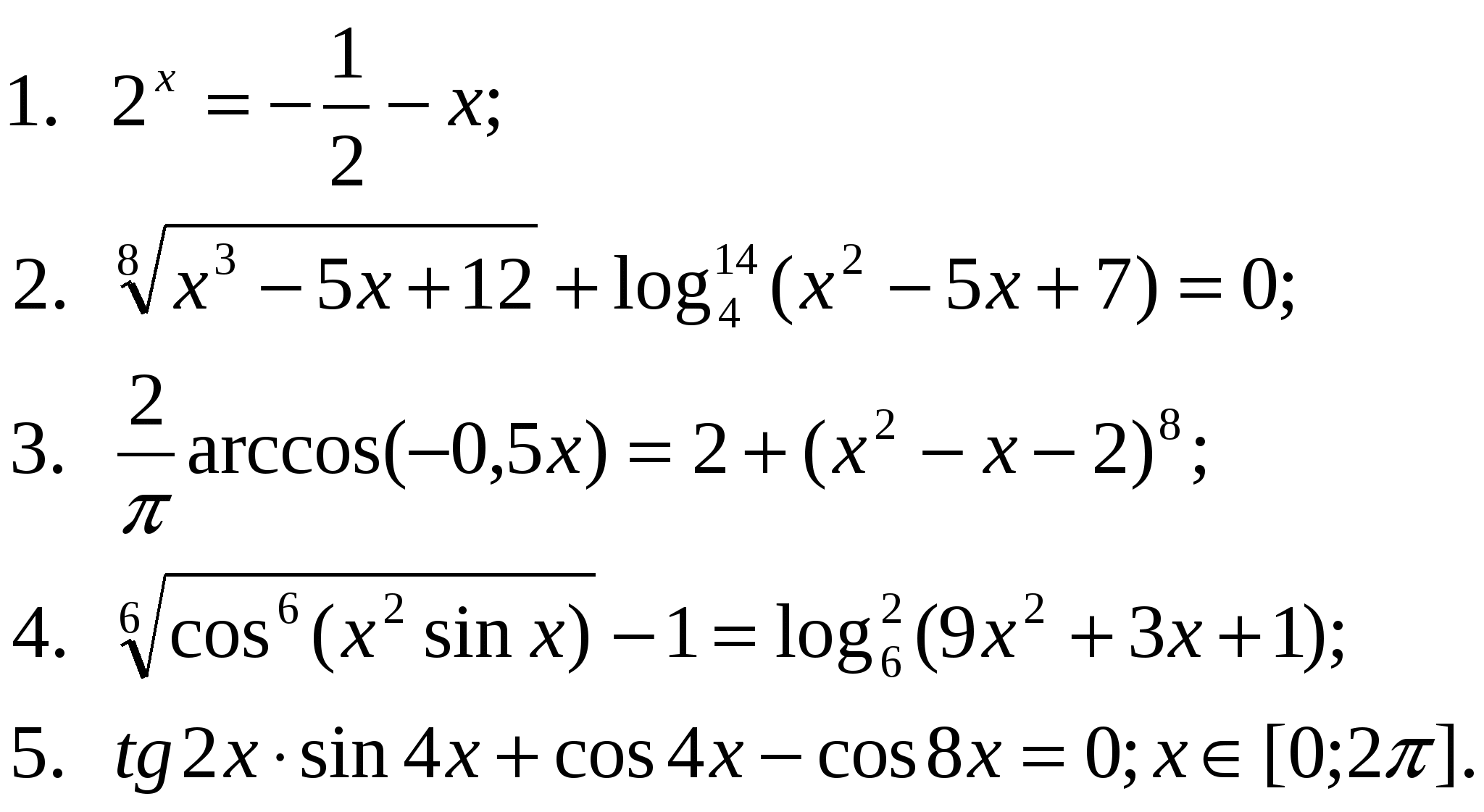