Рабочая программа по математике (указать учебный предмет, курс) Уровень общего образования (класс)
 Скачать 2.7 Mb. Скачать 2.7 Mb.
|
Результаты изучения учебного предмета В ходе преподавания математики в 5 классе, работы над формированием у обучающихся перечисленных в программе знаний и умений следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:
Программа обеспечивает достижение обучающимися следующих личностных, метапредметных и предметных результатов. Личностные результаты
Метапредметные результаты
Предметные результаты
Содержание и объем материала, подлежащего проверке, определяется программой. При проверке усвоения материала нужно выявлять полноту, прочность усвоения учащимися теории и умения применять ее на практике в знакомых и незнакомых ситуациях. Используемые формы, способы и средства проверки и оценки результатов обучения.
Ответ оценивается отметкой «5», если:
Отметка «4» ставится в следующих случаях:
Отметка «3» ставится, если:
Отметка «2» ставится, если:
Ответ оценивается отметкой «5», если ученик:
Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:
Отметка «3» ставится в следующих случаях:
Отметка «2» ставится в следующих случаях:
При оценке знаний, умений и навыков учащихся следует учитывать все ошибки (грубые и негрубые) и недочёты. 3.1. Грубыми считаются ошибки:
3.2. К негрубым ошибкам следует отнести:
3.3. Недочетами являются:
- небрежное выполнение записей, чертежей, схем, графиков.
Таблица показывает, сколько баллов минимум надо набрать при выполнении заданий обязательной и дополнительной частей для получения оценки «Зачет», «4», «5».
В рабочей программе предусмотрено 15 контрольных работ по темам:
Приложение 1 Вводная диагностическая контрольная работа по математике 5 класс 1 вариант № 1. Выполнить вычисления: а) 9087 – 5628 + 3435; б) 4964 : 73. № 2. Решить уравнение: а) х – 824 = 1013; б) 3591 : х = 63. № 3. Вычислите площадь и периметр прямоугольника со сторонами 6 см и 1 дм. Постройте его. № 4. В 5 класс ходят 14 учеников, а в 6 класс на 3 ученика больше. Сколько учеников ходит в оба класса? Вводная диагностическая контрольная работа по математике 5 класс 2 вариант № 1. Выполнить вычисления: а) 9283 – 4699 + 3424; б) 5992 : 56. № 2. Решить уравнение: а) х + 248 = 446; б) х : 12 = 348. № 3. Вычислите площадь и периметр прямоугольника со сторонами 40 мм и 5 см. Постройте его. № 4. В первой корзине лежат 15 яблок, а во второй на 3 яблока меньше. Сколько яблок лежит в обеих корзинах? Вводная диагностическая контрольная работа по математике 5 класс 3 вариант № 1. Выполнить вычисления: а) 9064 – 3298 + 2243; б) 7236 : 67. № 2. Решить уравнение: а) х – 247 = 465; б) 741 : х = 39. № 3. Вычислите площадь и периметр прямоугольника со сторонами 4 см и 1 дм. Постройте его. № 4. В первом ящике сидят 17 утят, а во втором на 2 утёнка больше. Сколько утят сидит в обоих ящиках? Вводная диагностическая контрольная работа по математике 5 класс 4 вариант № 1. Выполнить вычисления: а) 9158 – 5369 + 1714; б) 6634 : 62. № 2. Решить уравнение: а) х – 170 = 350; б) х : 7 = 560. № 3. Вычислите площадь и периметр прямоугольника со сторонами 30 мм и 4 см. Постройте его. № 4. В первой машине везли 25 досок, а во второй на 7 досок больше. Сколько досок перевозили на обеих машинах? Контрольная работа №1 по теме «Натуральные числа и шкалы».
Контрольная работа №2 по теме «Сложение и вычитание натуральных чисел». Контрольная работа №2 по теме «Сложение и вычитание натуральных чисел». Вариант 1 1. Выполните действие: а) 249 638 + 83 554; б) 665 247 – 8296. 2. а) Какое число на 28 763 больше числа 9338? б) На сколько число 59 345 больше числа 53 568? в) На сколько число 59 345 меньше числа 69 965? 3. В одном ящике 62 кг яблок, что на 18 кг больше, чем во втором. Сколько килограммов яблок во втором ящике? 4. В треугольнике MFK сторона FK равна 62 см, сторона КМ на 1 дм больше стороны FK, а сторона MF – на 16 см меньше стороны FK. Найдите периметр треугольника MFK и выразите его в дециметрах. 5. Вдоль аллеи (по прямой) высадили 15 кустов. Расстояние между любыми двумя соседними кустами одинаковое. Найдите это расстояние, если между крайними кустами 210 дм. Вариант 2 1. Выполните действие: а) 692 545 + 39 647; б) 776 348 – 9397. 2. а) Какое число на 37 874 больше числа 8137? б) На сколько число 38 954 больше числа 22 359? в) На сколько число 38 954 меньше числа 48 234? 3. В синей коробке 56 игрушек, что на 16 игрушек меньше, чем в красной коробке. Сколько игрушек в красной коробке? 4. В треугольнике BNP сторона NP равна 73 см, сторона BP на 1 дм меньше стороны NP, а сторона BN – на 11 см больше стороны NP. Найдите периметр треугольника BNP и выразите его в дециметрах. 5. Вдоль шоссе (по прямой) высадили 20 деревьев. Расстояние между любыми двумя соседними деревьями одинаковое. Найдите это расстояние, если между крайними деревьями 380 м Контрольная работа №3 по теме «Уравнение». Вариант 1 1. Найдите значение выражения 375 + а – 175 при а=89. 2. Решите уравнение: а) 87 – х = 39 ; б) z + 24 = 43 ; в) 108 – (90+х)=15. 3. Запишите выражение: На отрезке АВ отмечена точка М . Найти длину отрезка АВ , если отрезок АМ равен 35 см , а отрезок МВ короче отрезка АМ на m см. Упростите получившееся выражение и найдите его значение при m = 24 и при m = 37 . 4. Вычислите наиболее рациональным способом: а) 9037+(2001 – 1037); б) 8568 – 250 – 4568. 5. Решите задачу с помощью уравнения: «В автобусе было 48 пассажиров, после того, как из него несколько человек вышли, а 8 – вошли, в автобусе стало 29 пассажиров. Сколько человек вышли на остановке? Контрольная работа №3 по теме «Уравнение». Вариант 2 1. Найдите значение выражения 289 – b +111 при b=98. 2. Решите уравнение: а) у – 27 = 45 ; б) 37 + х = 64 ; в) 409 – (b+109)=202. 3. Запишите выражение: На отрезке АВ отмечены точки С и D так, что точка D лежит между точками С и В. Найти длину отрезка DB , если АВ = 56 см , АС = 16 см и CD = n см. Упростите получившееся выражение и найдите его значение при n = 18 и при n = 29. 4. Вычислите наиболее рациональным способом: а) 9047+(1999 – 1047); б) 6882 – 350 – 2882. 5. Решите задачу с помощью уравнения: «На складе было 197 станков. После того, как часть продали, а еще 86 привезли, на складе осталось еще 115 станков. Сколько всего станков продали?» Контрольная работа №4 по теме «Умножение и деление натуральных чисел». Вариант 1 №1 Найдите значение выражения: а) 58∙196 б) 405∙208 в) 36490:178 №2 Решите уравнение а) х∙14=112 б) 133:у=19 в) m:15=90 №3 Вычислите, выбирая удобный порядок действий. а) 4∙289∙25 б) 50∙97∙20 №4 Задача. Коля задумал число, умножил его на 3 и от произведения отнял 7. Он получил 50. Какое число задумал Коля? №5 Угадайте корень уравнения и сделайте проверку: х+х – 20=х+5 Контрольная работа №4 по теме «Умножение и деление натуральных чисел». Вариант 2 №1 Найдите значение выражения: а) 67∙189 б) 306∙805 в) 38130:186 №2 Решите уравнение а) х∙13=182 б) 187:у=17 в) n:14=98 №3 Вычислите, выбирая удобный порядок действий. а) 25∙197∙4 б) 50∙23∙40 №4 Задача. Света задумала число, умножила его на 4 и к произведению прибавила 8. Получила 60. Какое число задумала Света? №5 Угадайте корень уравнения и сделайте проверку: у+у – 25=у+10 Контрольная работа №5 по теме «Упрощение выражений. Квадрат и куб числа» Вариант 1 1) Найдите значение выражения: а) 684 397 – 584 397; б) 39 58 – 9720 : 27 + 33; в) 23 + 32. 2) Решите уравнение: а) 9у – 3у = 666; б) 3х + 5х = 1632. 3) Задача: В двух зрительных залах кинотеатра 624 места. В одном зале в 3 раза больше мест, чем в другом. Сколько мест в меньшем зрительном зале? 4) Упростите выражение 36х + 124 + 16х и найдите его значение при х = 5 и при х = 10. 5) Задача : У Лены столько же двухкопеечных монет, сколько и трёхкопеечных. Все монеты составляют сумму 40 коп. Сколько двухкопеечных монет у Лены ? Контрольная работа №5 по теме «Упрощение выражений. Квадрат и куб числа» Вариант 2 1) Найдите значение выражения: а) 798 349 – 798 249; б) 57 38 – 8640 : 24 + 66; в) 52 + 33. 2) Решите уравнение: а) 4а + 8а = 204 ; б) 12у – 7у = 315 . 3) Задача: В двух пачках 168 тетрадей. В одной пачке в 3 раза меньше тетрадей, чем в другой. Сколько тетрадей в меньшей пачке ? 4) Упростите выражение 147 + 23х + 39х и найдите его значение при х = 3 и при х = 10 . 5) Задача : У Коли несколько трёхкопеечных и несколько пятикопеечных монет. Всего 80 коп. Трёхкопеечных монет у него столько же, сколько и пятикопеечных. Сколько трёхкопеечных монет у Коли ? Контрольная работа №6 по теме «Площади и объёмы» Вариант 1 1). Найдите по формуле s = vt : а). путь s, если v = 105 км/ч , t = 12 ч ; б). скорость v, если s = 168 м , t = 14 мин . 2). Задача : Ширина прямоугольного участка земли 500 м, и она меньше длины на 140 м. Найдите площадь участка и выразите её в гектарах. 3). Задача : Ширина прямоугольного параллелепипеда 12 см, длина в 3 раза больше, а высота на 3 см больше ширины. Найдите объём прямоугольного параллелепипеда. 4). Найдите значение выражения 15600 : 65 + 240 ∙ 86 – 20550 . 5). Задача : Ширина прямоугольника 23 см . На сколько увеличится площадь этого прямоугольника, если его длину увеличить на 3 см ? Контрольная работа №6 по теме «Площади и объёмы» Вариант 2 1). Найдите по формуле s = vt : а). путь s , если t = 13 ч , v = 408 км/ч ; б). время t , если s = 7200 м , v = 800 м/мин . 2). Задача : Длина прямоугольного участка земли 650 м , а ширина на 50 м меньше. Найдите площадь участка и выразите её в гектарах. 3). Задача : Длина прямоугольного параллелепипеда 45 см, ширина в 3 раза меньше длины, а высота на 2 см больше ширины.. Найдите объём параллелепипеда . 4). Найдите значение выражения 17040 – 69 · 238 – 43776 : 72 . 5). Задача : Длина прямоугольника 84 см. На сколько уменьшится площадь прямоугольника, если его ширину уменьшить на 5 см ? Контрольная работа №7 по теме «Обыкновенные дроби» Вариант 1 1). Задача : В драматическом кружке занимаются 28 человек. Девочки составляют 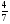 всех участников кружка. Сколько девочек занимаются в драматическом кружке ? всех участников кружка. Сколько девочек занимаются в драматическом кружке ? 2). Задача : Возле школы растут только берёзы и сосны. Берёзы составляют 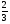 всех деревьев. Сколько деревьев возле школы, если берёз 42 ? всех деревьев. Сколько деревьев возле школы, если берёз 42 ?3). Сравните: а). 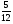 и и 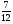 ; ;б). 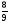 и и 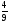 . .4). Какую часть составляют : а). 7 дм 3 от кубического метра ; б). 17 мин от суток ; в). 5 коп. от 12 руб. ? 5). При каких натуральных значениях m дробь 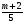 будет правильной ? будет правильной ?Контрольная работа №7 по теме «Обыкновенные дроби» Вариант 2 1). Задача : Длина прямоугольника 56 см. ширина составляет 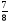 длины. Найдите ширину прямоугольника. длины. Найдите ширину прямоугольника.2). Задача : На районной олимпиаде 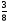 числа участников получили грамоты. Сколько участников было на олимпиаде, если грамоты получили 48 человек. числа участников получили грамоты. Сколько участников было на олимпиаде, если грамоты получили 48 человек.3). Сравните: а). 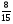 и и 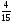 ; ;б). 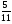 и и 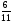 . .4). Какую часть составляют : а). 19 га от квадратного километра ; б). 39 ч от недели ; в). 37 г от 5 кг ? 5). При каких натуральных значениях k дробь 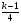 будет правильной ? будет правильной ?Контрольная работа №8 по теме «Сложение и вычитаний дробей с одинаковыми знаменателями» Вариант 1 1. Выполните действия: а) – + ; в) 6 – 2 ; б) 4 + 3 ; г) 5 – 1 . 2. Задача : За два дня пропололи 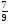 огорода, причём в первый день пропололи огорода, причём в первый день пропололи 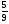 огорода. Какую часть огорода пропололи за второй день ? огорода. Какую часть огорода пропололи за второй день ?3. Задача : На первой автомашине было 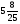 т груза. Когда с неё сняли т груза. Когда с неё сняли 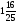 т груза, то на первой машине груза стало на т груза, то на первой машине груза стало на 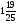 т меньше, чем на второй. Сколько всего тонн груза было на двух автомашинах первоначально ? т меньше, чем на второй. Сколько всего тонн груза было на двух автомашинах первоначально ?4. Решите уравнение: а) 5 – х = 3 ; б) у + 4 = 10 . 5. Какое число надо разделить на 8, чтобы частное равнялось 5 ? Контрольная работа №8 по теме «Сложение и вычитаний дробей с одинаковыми знаменателями» Вариант 2 1. Выполните действия: а) – + ; в) 7 – 3 ; б) 5 + 1 ; г) 6 – 4 . 2. Задача : За день удалось от снега расчистить 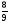 аэродрома. До обеда расчистили аэродрома. До обеда расчистили 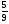 аэродрома. Какую часть аэродрома очистили от снега после обеда ? аэродрома. Какую часть аэродрома очистили от снега после обеда ?3. Задача : На приготовление домашних заданий ученица рассчитывала потратить 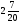 ч , но потратила на ч , но потратила на 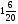 ч больше. На просмотр кинофильма по телевизору она потратила на ч больше. На просмотр кинофильма по телевизору она потратила на 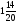 ч меньше, чем на приготовление домашних заданий. Сколько всего времени потратила ученица на приготовление домашних заданий и на просмотр кинофильма? ч меньше, чем на приготовление домашних заданий. Сколько всего времени потратила ученица на приготовление домашних заданий и на просмотр кинофильма?4. Решите уравнение: а) х + 2 = 4 ; б) 6 – у = 3 . 5. Какое число надо разделить на 6, чтобы частное равнялось 8 Контрольная работа №9 по теме «Десятичные дроби. Сложение и вычитание десятичных дробей» Вариант 1 1). Сравните: а). 2,1 и 2,099 ; б). 0,4486 и 0,45 . 2). Выполните действия: а). 56,31 – 24,246 – ( 3,87 + 1,03 ) ; б). 100 – ( 75 + 0,86 + 19,34 ). 3). Задача : Скорость катера против течения 11,3 км/ч. Скорость течения 3,9 км/ч. Найдите собственную скорость катера и его скорость по течению. 4). Округлите: а). 6,235 ; 23,1681 ; 7,25 до десятых ; б). 0,3864 ; 7,6231 до сотых ; в). 135,24 и 227,72 до единиц. 5). Запишите четыре значения т, при которых верно неравенство 0,71 < т < 0,74. Контрольная работа №9 по теме «Десятичные дроби. Сложение и вычитание десятичных дробей» Вариант 2 1). Сравните: а). 7,189 и 7,2 ; б). 0,34 и 0,3377 . 2). Выполните действия: а). 61,35 – 49,561 – ( 2,69 + 4,01 ) ; б). 1000 – ( 0,72 + 81 – 3,968 ). 3). Задача : Скорость теплохода по течению реки 42,8 км/ч. Скорость течения 2,8 км/ч. Найдите собственную скорость теплохода и его скорость против течения. 4). Округлите: а). 3,062 ; 4,137 ; 6,455 до сотых ; б). 5,86 ; 14,25 и 30,22 до десятых ; в). 247,54 и 376,37 до единиц. 5). Запишите четыре значения п, при которых верно неравенство 0,65 < п < 0,68. Контрольная работа №10 по теме «Умножение и деление десятичных дробей на натуральные числа» Вариант 1 1). Выполните действие: а). 0,308 · 12 ; г). 4 : 32 ; б). 3,84 · 45 ; д). 126,385 10; в). 3,074 : 53 ; е). 126,385 : 100. 2). Найдите значение выражения 50 – 27 · ( 27,2 : 17 ) 3). Задача: 5 упаковок пряников и 3 торта вместе весят 5,1 кг. Сколько весит 1 упаковка пряников, если один торт весит 0,9 кг ? 4). Решите уравнение: а). 8у + 5,7 = 24,1; б). ( 9,2 – х ): 6 = 0,9. 5). Если в некоторой десятичной дроби перенести запятую вправо через один знак, то она увеличится на 23,49. Найдите эту дробь. Контрольная работа №10 по теме «Умножение и деление десятичных дробей на натуральные числа» Вариант 2 1). Выполните действие: а). 0,507 · 39; г). 5 : 16 ; б). 3,84 · 45; д). 234,166 100; в). 3,216 : 67 ; е). 234,166 : 10. 2). Найдите значение выражения 40 – 26 · ( 26,6 : 19 ). 3). Задача: 6 коробок печенья и 5 коробок шоколадных конфет весят 6,2 кг. Сколько весит 1 коробка конфет, если 1 коробка печенья весит 0,6 кг ? 4). Решите уравнение: а). 9х + 3,9 = 31,8 ; б). ( у + 4,5 ) : 7 = 1,2 . 5). Если в некоторой десятичной дроби перенести запятую через один знак влево, то она уменьшится на 2,25. Найдите эту дробь. Контрольная работа №11 по теме «Умножение и деление десятичных дробей» Вариант 1 1). Выполните действие: а). 4,125 ∙ 1,6; б). 0,042 ∙ 7,3; в). 29,64 : 7,6; г). 7,2 : 0,045. 2). Найдите значение выражения ( 18 – 16,9 ) ∙ 3,3 – 3 : 7,5 3). С кондитерской фабрики отгрузили 20 коробок мармелада по 1,3 кг в коробке и 30 коробок по 1,1 кг мармелада. Сколько весит в среднем одна коробка ? 4). Поезд 3 ч шел со скоростью 63,2 км/ч и 4 ч со скоростью 76,5 км/ч. Найдите среднюю скорость поезда на всем пути. 5). Сумма трех чисел 10,23, а среднее арифметическое шести других чисел 2,9. Найдите среднее арифметическое всех этих девяти чисел. Контрольная работа №11 по теме «Умножение и деление десятичных дробей» Вариант 2 1). Выполните действие: а). 3,2 ∙ 5,125; б). 0,084 ∙ 6,9; в). 60,03 : 8,7; г). 36,4 : 0,065 2). Найдите значение выражения ( 21 – 18,3 ) ∙ 6,6 + 3 : 0,6 3). В магазин привезли 10 ящиков яблок по 3,6 кг в одном ящике и 40 ящиков яблок по 3,2 кг в ящике. Сколько в среднем килограммов яблок в одном ящике ? 4). Легковой автомобиль шел 2 ч со скоростью 55,4 км/ч и еще 4 ч со скоростью 63,5 км/ч. Найдите среднюю скорость автомобиля на всем пути. 5). Среднее арифметическое пяти чисел 4,7, а сумма других трех чисел 25,14. Найдите среднее арифметическое всех этих восьми чисел. Контрольная работа №12 по теме «Проценты» Вариант 1 1). Выполните действия: 0,81 : 2,7 + 4,5 ∙ 0,12 – 0,69 2). Задача: В понедельник привезли 31,5 т моркови, во вторник – в 1,4 раза больше, чем в понедельник, в среду – на 5,4 т меньше, чем во вторник. Сколько тонн моркови привезли на склад за эти три дня ? 3). Задача: В школьном саду 40 фруктовых деревьев. 30 % этих деревьев – яблони. Сколько яблонь в школьном саду ? 4). Задача: В библиотеке 12 % всех книг – словари. Сколько книг в библиотеке, если словарей в ней 900? 5). Решить уравнение: а). 8у + 5,7 = 24,1 ; б). ( 9,2 – х ) : 6 = 0,9 6). От мотка провода отрезали сначала 30 %, а затем еще 60 % остатка. После этого в мотке осталось 42 м провода. Сколько метров провода было в мотке первоначально? Контрольная работа №12 по теме «Проценты» Вариант 2 1). Выполните действия: 3,8 ∙ 0,15 – 1,04 : 2,6 + 0,83 2). Задача: Имелось три куска материи. В первом куске было 19,4 м, во втором – на 5,8 м больше, чем в первом, а в третьем куске было в 1,2 раза меньше, чем во втором. Сколько метров материи было в трёх кусках вместе ? 3). Задача: В книге 120 страниц. Рисунки занимают 35 % книги. Сколько страниц занимают рисунки ? 4). Задача: За день вспахали 18 % поля. Какова площадь всего поля, если вспахали 1170 га? 5). Решить уравнение: а). 9х + 3,9 = 31,8 б). ( у + 4,5 ) : 7 = 1,2 6). Израсходовали сначала 40 % имевшихся денег, а затем еще 30 % оставшихся. После этого осталось 105 р. Сколько денег было первоначально? 1. Постройте углы, если: а) ВМЕ = 68; б) СКР = 115. 2. Начертите AKN такой, чтобы А = 120. Измерьте и запишите градусные меры остальных углов треугольника. 3. Луч ОК делит прямой угол DOS на два угла так, что угол DOK составляет 0,7 угла DOS. Найдите градусную меру угла KOS. 4. Развернутый угол AMF разделен лучом МС на два угла АМС и CMF. Найдите градусные меры этих углов, если угол АМС вдвое больше угла CMF. 5. Из вершины развернутого угла DKP проведены его биссектриса КВ и луч КМ так, что ВКМ = 38. Какой может быть градусная мера угла DKM ? Контрольная работа №13 по теме «Измерение углов. Транспортир» Вариант 1 Контрольная работа №13 по теме «Измерение углов. Транспортир» Вариант 2 1. Постройте углы, если: а) ADF = 110; б) HON = 73. 2. Начертите BCF такой, чтобы В = 105. Измерьте и запишите градусные меры остальных углов треугольника. 3. Луч АР делит прямой угол CAN на два угла так, что угол NAP составляет 0,3 угла CAN. Найдите градусную меру угла PAC. 4. Развернутый угол BOE разделен лучом OT на два угла BOT и TOE. Найдите градусные меры этих углов, если угол BOT втрое меньше угла TOE. 5. Из вершины развернутого угла MNR проведены его биссектриса NB и луч NP так, что ВNP = 26. Какой может быть градусная мера угла MNP ? Итоговая контрольная работа №14 Вариант 1 1. Вычислите: 2,66 : 3,8 – 0,81 0,12 + 0,0372. 2. В магазине 240 кг фруктов. За день продали 65 % фруктов. Сколько килограммов фруктов осталось? 3. Найдите высоту прямоугольного параллелепипеда, объем которого равен 25,2 дм3, длина 3,5 дм и ширина 16 см. 4. Решите уравнение: 2,3у + 31+ 2,5у = 67. 5. Постройте углы МОК и КОС, если МОК = 110, КОС = 46. Какой может быть градусная мера угла СОМ ? Итоговая контрольная работа №14 Вариант 2 1. Вычислите: 7,8 0,26 – 2,32 : 2,9 + 0,672. 2. В цистерне 850 л молока. 48 % молока разлили в бидоны. Сколько молока осталось в цистерне? 3. Объем прямоугольного параллелепипеда 1,35 м3, высота 2,25 м и длина 8 дм. Найдите его ширину. 4. Решите уравнение: 13 + 3,2х + 0,4х = 40. 5. Постройте углы ADN и NDB, если ADN = 34, NDB = 120. Какой может быть градусная мера угла ADB ? Перечень тестов Тест 1по теме «Натуральные числа» Тест 2 по теме «Сложение и вычитание натуральных чисел» Тест 3 по теме «Числовые и буквенные выражения» Тест 4 по теме «Уравнение» Тест 5 по теме «Умножение натуральных чисел» Тест 6 по теме «Деление натуральных чисел» Тест 7 по теме «Обыкновенные дроби» Тест 8 по теме «Действия с обыкновенными дробями» Тест 9 по теме «Десятичные дроби» Тест 10 по теме «Сложение десятичных дробей» Тест 11 по теме «Вычитание десятичных дробей» Тест 12 по теме «Умножение десятичных дробей» Тест 13 по теме «Деление десятичных дробей» Тест 14 по теме «Проценты» Приложение 2 ТЕСТ 1 НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ Вариант 1 Выполните задания, ответьте на вопросы (верный ответ подчеркните).
а) 320 003; 6)3 023 000; в) 3 002 003; г) 3 020 003.
а) 310 001, 31 109,31 099; б) 310 001,31 099,31 109; в) 31 109,31 099,310 001; г) 31 099,31 109,310 001.
а) 888; б) 8008; в) 800 008; г) 80 088.
а) 56 000+200+70; б) 50 000+6000+270; в) 50 000+6000+200+70; г) 56 000+270.
а) 553 533; 6) 533 553; в) 555 333; г) 535 353.
а) 18 999; б) 1899; в) 189 999; г) 180 999.
а) один миллион десять тысяч сто; б) сто одна тысяча сто; в) десять миллионов сто одна тысяча; г) сто одиннадцать тысяч сто. 8*. На сколько отличается число 50000 + 4000 + 200 + 30 + 5 от числа 40000 + 3000 + 100 + 20 + 4? а) на 1111; б)на 1; в) на 11; г) на 11111 ТЕСТ 1 НАТУРАЛЬНЫЕ ЧИСЛА И ШКАЛЫ Вариант 2
а) 50 400 009; б) 50 004 009; в) 54 000 009; г) 50 040 090.
а) 73 204, 73 199, 732 001; б) 73 199, 73 204, 732 001; в) 732 001,73 204, 73 199; г) 732 001,73 199, 73 204.
а) 555; 6) 5550; в) 50 005; г) 500 500.
а) 83 000 + 610; б) 80 000 + 3000 + 600+ 10; в) 80 000 + 3600+ 10; г) 83 000 + 600 + 10.
а) 949 494; б) 994 944; в) 999 444; г) 949 944.
а) 190 000; б) 199 099; в) 199 999; г) 19 999.
а) один миллион десять тысяч сто; б) сто одна тысяча сто; в) десять миллионов сто одна тысяча; г) сто одиннадцать тысяч сто. 8*. На сколько отличается число 50000 + 8000 + 800 + 80 + 8 от числа 50000 + 7000 + 700 + 70 + 7? а) на 1111; б) на1; в) на 11; г) на 11111. ТЕСТ 2 СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 1 Подчеркните верный ответ или предложите свой.
а) да; в) не знаю; б) нет; г) свой ответ
а) да; в) не знаю; б) нет; г) свой ответ
а) да; в) не знаю; б) нет; г) свой ответ
а) 2; в) 6; б) 1; г) свой ответ
а) разностью; в) суммой; б) произведением; г) свой ответ 6. Если уменьшаемое 12 784, вычитаемое 9 386, то разность равна: а) 22 170; в) 3398; б) 3 389; г) свой ответ 7. При выполнении вычитания чисел 5 837 и 45 в столбик правильной является запись: 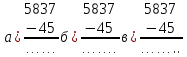 г) свой ответ г) свой ответ
а) 11 ООО; в) 4 098; б) 10 990; г) свой ответ
а) 105 087; в) 165 167; б) 104 087; г) свой ответ.
а) 15+ 18 =15- 18; б) 15+ 18= 18-15; в) 15 + 18= 18+ 15; г) свой ответ . 11. Свойство вычитания суммы из числа для числа 10 и суммы 3 и 1 записывается так: а) 10-(3 + 1) = (10-3)-1; в) 10-(3 + 1)= 10-3 + 1; б) (10 + 3) - 1 = 10 - (3 + 1); г) свой ответ 12*. Чему равна разность самого большого и самого маленького из чисел, составленных из цифр 1, 3 и 5? (В любом числе каждая цифра используется только один раз.) а) 396; в) 777; б)216; г) свой ответ ТЕСТ 2 СЛОЖЕНИЕ И ВЫЧИТАНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 2 Подчеркните верный ответ или предложите свой.
а) да; в) не знаю; б) нет; г) свой ответ
а) да; в) не знаю; б) нет; г) свой ответ
а) да; в) не знаю; б) нет; г) свой ответ
а) 1; в) 5; б) 6; г) свой ответ
а) разностью; в) частным; б) суммой; г) свой ответ
а) 22 170; в) 3398; б) 22 160; г) свой ответ
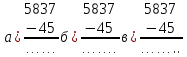 г)свой ответ г)свой ответ
а) 4098; в) 4 198; б) 11 ООО; г) свой ответ .
а) 105 185; в) 138 265; б) 104 185; г) свой ответ
а) (3 + 6) + 7 = 3 + (6 + 7); в) (7 - 3) - 6 = (7 - 6) - 3; б) (7 - 3) + 6 = 7 + (6 - 3); г) свой ответ .
а) (2 + 5)-3 = (5-3) + 2 в)(2 + 3) - 5 = (5 - 3) + 2 б) 5 - (3 + 2) = (5 - 2) – 3 г)свой ответ.
а) 672; в) 396; б) 888; г) свой ответ. Тест 3 ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Вариант 1 Ответьте на вопросы, выполните задания (подчеркните верный ответ или предложите свой).
а) (18-7) +а; в)х + 10 = 28; б) 36 : 6 + 7; г) свой ответ.
а) 471; в) 437; б) 447; г) свой ответ.
а) 26; в) 42; б) 25; г) свой ответ.
а) а + (в + с) = (а + в) + с; в) а + в=в+ а; б) а-в = в-а г) свой ответ.
а) а - (в+ с) = а - в + с; в)a-(b +c) =a-b-c; б)(а + в)- с= a-в– с; г) свой ответ.
а) 18; в) 20; б) 13; г) свой ответ.
а) 30 км/ч; в) 40 км/ч; б) 1440 км; г) свой ответ. 8*. Чему равна сумма наибольшего трехзначного числа и трех последу ющих чисел? а) 3606; в) 4002; б) 3990; г) свой ответ. Тест 3 ЧИСЛОВЫЕ И БУКВЕННЫЕ ВЫРАЖЕНИЯ Вариант 2 Ответьте на вопросы, выполните задания (подчеркните верный ответ или предложите свой).
а) (18 - 7) + а; в)х+ 10 = 28; б) 36 : 6 + 7; г) свой ответ.
а) 461; в) 457; б) 447; г) свой ответ.
а) 31; в) 18; б) 21; г) свой ответ.
а) а + (в + с) = (а + в) + с; в) а + в =в + а; б) a- в =в-а; г) свой ответ.
а) (а + в) - с = а + (в - с); в) (а + в) - с = а - в+ с; б)a-(b + с)-с = а-в-с; г) свой ответ.
а) 18; в) 13; б) 20; г) свой ответ.
а) 3 ч; в) 19 200 км; б) 4 ч; г) свой ответ. 8*. Чему равна сумма наименьшего трехзначного числа и трех предшествующих чисел? а) 406; в) 394; б)390; г) свой ответ . Тест 4. УРАВНЕНИЕ Вариант 1 Выберите и подчеркните верное утверждение или предложите свое.
а) числовое выражение, значение которого нужно найти; б) буквенное выражение, значение которого нужно найти; в) равенство, содержащее букву, значение которой нужно найти; г) свой ответ.
а) корни или убедиться, что их нет; б) сумму; в)корни; г) свой ответ
а) к разности прибавить вычитаемое; б) из разности вычесть вычитаемое; в) разность умножить на вычитаемое; г) свой ответ.
а) 50; б) 16; в) 40; г) свой ответ.
а) вычитаемое; в) разность; б) уменьшаемое; г) свой ответ.
а) 144; б) х в) 25; г) свой ответ.
а) 133; б) 77; в) 67; г) свой ответ. 8*. Сумма трех слагаемых равна 77 777. Одно слагаемое равно 3 333, вто рое 444, тогда третье слагаемое равно: а) 74 000; б) 81 554; в) 100 444; г) свой ответ. Тест 4. УРАВНЕНИЕ Вариант 2 Выберите и подчеркните верное утверждение или предложите свое.
а) буквенным выражением; б) числовым выражением; в) уравнением; г) свой ответ.
а) верное буквенное равенство; б) верное числовое равенство; в) верное выражение; г) свой ответ.
а) к разности прибавить уменьшаемое; б) из уменьшаемого вычесть разность; в) уменьшаемое умножить на разность; г) свой ответ
а) 43; б) 53; в) 21; г) свой ответ.
а) вычитаемое; в) разность; б) уменьшаемое; г) свой ответ.
а) 25; б) 169; в) 119; г) свой ответ.
а) 144; б) 56; в) 66; г) свой ответ. 8*. Сумма трех слагаемых равна 99 999. Одно слагаемое равно 1111, а второе 888, тогда третье слагаемое равно: а) 101 998; б) 98 000; в) 100 888; г) свой ответ. Тест 5 УМНОЖЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 1 Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
а) 19; в) 722; б) 2; г) свой ответ.
а) 0; в) а; б) 1; г) свой ответ.
а) 54 652; в) 54 651; б) 1; г) свой ответ.
а) 17214; в) 809; б)153114; г) свой ответ.
а) 5130; в) 51300; б)613; г) свой ответ.
а) 18 +с; в) 18 • с • с; б) 18 • с; г) свой ответ.
а) 4 • а+ 11; в) а+ 44; б) 4 • а + 44; г) свой ответ.
а) 12 км/ч; в) 108 км/ч; б) 108 км; г) свой ответ. 9*. Чему равно наибольшее произведение двух различных двузначных чи сел, составленных из цифр 1, 2, 3 и 4 (должна использоваться каждая цифра и только один раз)? а) 903; в) 1462; б) 1312; г) свой ответ. Тест 5 УМНОЖЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 2 Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
а) 4; в) 60; б) 576; г) свой ответ.
а) а; в) 1; б) 0; г) свой ответ.
а)765095; в)7650950; б) 0 г) свой ответ.
а) 416; в) 33463; б) 44363; г) свой ответ.
а) 56; в) 56 000; б) 15 000; г) свой ответ.
а) 8 - х; в) 8 • х •х; б) 8 • х; г) свой ответ.
а) 3 • a + 36; в) а + 36; б) 3 • а + 12; г) свой ответ.
а) 11; в) 48; б) 176; г) свой ответ. 9*. Чему равно наибольшее произведение двух различных двузначных чи сел, составленных из цифр 1, 2, 3 и 5 (должна использоваться каждая цифра и только один раз)? а) 2916; в) 1632; б) 2142; г) свой ответ. Тест 6 ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 1 Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
а) 1; в) 7855; б) 7856; г) свой ответ .
а) 150; в) 9; б) 2025; г) свой ответ .
а) 304; в) 32940; б) 34; г) свой ответ .
а) 14; в) 104; б) 1365; г) свой ответ .
а) 125; в) 1250; б) 3780; г) свой ответ .
а) в 100 раз; в) в 4 раза; б) в 15 раз; г) свой ответ
а) 12; в) 1920; б) 120; г) свой ответ . 8*. Найдите два числа, если известно, что одно из них в 18 раз больше дру гого, а их сумма равна 1083. а) 85 и 998; в) 57 и 1026; б) 58 и 1102; г) свой ответ Тест 6 ДЕЛЕНИЕ НАТУРАЛЬНЫХ ЧИСЕЛ Вариант 2 Выполните задания, ответьте на вопросы (подчеркните верный ответ или предложите свой).
а) 1; в) 4583; б) 4584; г) свой ответ.
а) 5325718; в) 52; б) 502; г) свой ответ.
а) 18225; в) 450; б) 9; г) свой ответ
а) 13; в) 103; б) 29 767; г) свой ответ.
а) 506; в) 13 365; б) 132; г) свой ответ.
а) в 3 раза; в) в 2 раза; б) в 30 раз; г) свой ответ
а) 120 ч; в) 12 ч; б) 14700 км/ч; г) свой ответ 8*. Найдите два числа, если известно, что одно из них в 16 раз больше дру гого, а их разность равна 435. а) 464 и 29; в) 496 и 31; б) 458 и 23; г) свой ответ Тест 7 Обыкновенные дроби Вариант 1 Выберите и подчеркните верный или предложите свой.
а) натуральными числами; в) десятичными дробями; б) обыкновенными дробями; г) свой ответ. |
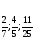 называются:
называются: