|
Рабочая программа по математике 11 класс (алгебра и начала анализа, геометрия) Пояснительная записка
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА с.Лутна
«Согласовано»: «Утверждаю»:
Зам. Директора по УВР Директор МБОУ СОШ с. Лутна
______________/____________/ ________________/____________/
«_____» сентября 201__г. «_____» сентября 201__г.
Рабочая программа учебного курса
Математика
Профильный уровень
11 класс
Количество часов: 238
Разработал учитель первой
квалификационной категории:
Бибикова О.А.
Рабочая программа по математике
11 класс
(алгебра и начала анализа, геометрия)
Пояснительная записка
Школьное образование в современных условиях призвано обеспечить функциональную грамотность и социальную адаптацию обучающихся на основе приобретения ими компетентностного опыта в сфере учения, познания, профессионально – трудового выбора, личностного развития, ценностных ориентаций и смыслотворчества. Это предопределяет направленность целей и задач обучения на формирование компетентной личности, способной к жизнедеятельности и самоопределению в информационном обществе, ясно представляющей свои потенциальные возможности, ресурсы и способы реализации выбранного жизненного пути.
Главной целью школьного образования является развитие ребёнка как компетентной личности путём включения его в различные виды ценностной человеческой деятельности: учеба, познание, коммуникация, профессионально – трудовой выбор, личностное саморазвитие, ценностные ориентации, поиск смыслов жизнедеятельности. С этих позиций обучение рассматривается как процесс овладения не только определенной суммой знаний и системой соответствующих умений и навыков, но и как процесс овладения компетенциями.
Это определило цели обучения математике:
формирование представлений об идеях и методах математики; о математике как универсальном языке науки, средстве моделирования явлений и процессов;
овладение устным и письменным математическим языком, математическими знаниями и умениями, необходимыми для изучения школьных естественно-научных дисциплин, для продолжения образования и освоения избранной специальности на современном уровне;
развитие логического мышления, алгоритмической культуры, пространственного воображения, развитие математического мышления и интуиции, творческих способностей на уровне, необходимом для продолжения образования и для самостоятельной деятельности в области математики и ее приложений в будущей профессиональной деятельности;
воспитание средствами математики культуры личности: знакомство с историей развития математики, эволюцией математических идей, понимание значимости математики для общественного прогресса.
На основании требований Государственного образовательного стандарта 2004 г. в содержании предполагается реализовывать актуальные в настоящее время компетентностный, деятельностный подходы, которые определяют задачи обучения:
приобретение математических знаний и умений;
овладение обобщенными способами мыслительной, творческой деятельностей;
освоение компетенций: учебно–познавательной, коммуникативной, рефлексивной, личностного развития, ценностно-ориентационной и профессионально-трудового выбора.
Рабочая программа по математике для 11 классов составлена к УМК С.М. Никольского и др. «Алгебра и начала анализа», 11 класс, М. «Просвещение», 2010 год и «Геометрия,10-11: Учебное пособие для общеобразовательных учреждений» Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- М.: Просвещение, 2010 на основе федерального компонента государственного стандарта общего образования
Рабочая программа составлена из расчёта 7 часов изучения математики в неделю:
5 часов по программам к УМК С.М. Никольского и др. «Алгебра и начала анализа», 11 класс, М. «Просвещение», 2010 год и и 2 часа «Геометрия,10 -11: Учебное пособие для общеобразовательных учреждений» и Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др.- М.: Просвещение, 2010 на основе федерального компонента государственного стандарта общего образования с учетом авторского тематического планирования учебного материала;
Таким образом: 5 часов – алгебра и начала анализа и 2 часа – геометрия.
Содержание программы по математике
I Блок Алгебра и начала анализа
2 Модуль. Функции и графики (23 часа).
Функции. Область определения и множество значений. График функции. График функции, аналитический способ задания, которой содержит переменную под знаком модуля. Построение графиков функций, заданных различными способами. Свойства функций: монотонность, четность и нечетность, периодичность, ограниченность. Промежутки возрастания и убывания, наибольшее и наименьшее значения, точки экстремума (локального максимума и минимума). Графическая интерпретация. Примеры функциональных зависимостей в реальных процессах и явлениях. Преобразования графиков: параллельный перенос, симметрия относительно осей координат и симметрия относительно начала координат, симметрия относительно прямой 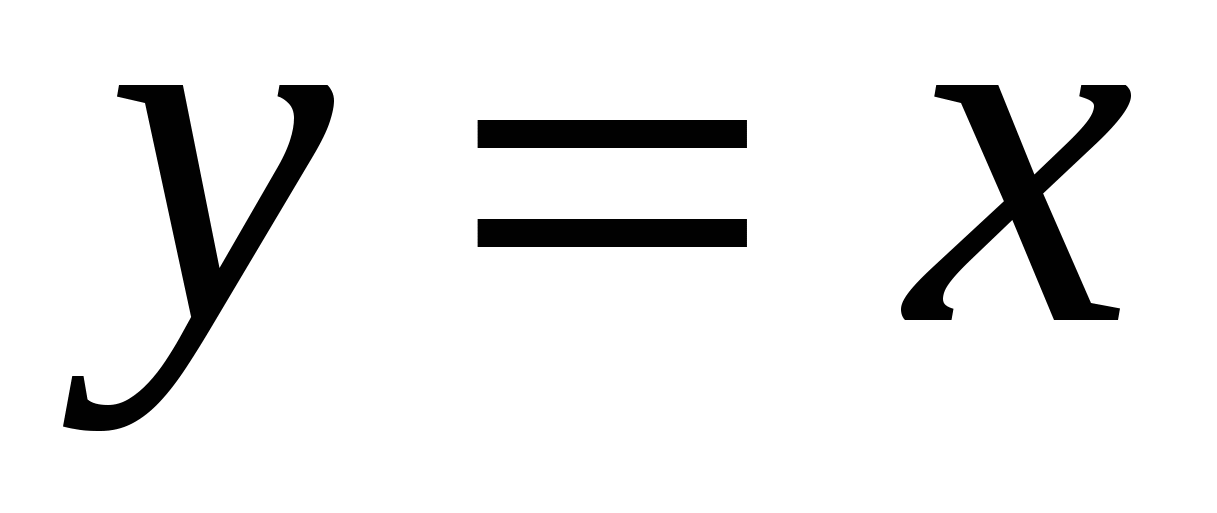 , растяжение и сжатие вдоль осей координат. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций. Обратная функция. Область определения и область значений обратной функции. График обратной функции. Понятие о непрерывности функции. , растяжение и сжатие вдоль осей координат. Вертикальные и горизонтальные асимптоты графиков. Графики дробно-линейных функций. Обратная функция. Область определения и область значений обратной функции. График обратной функции. Понятие о непрерывности функции.
3 Модуль. Производная функции и ее применение (30 часов).
Понятие о производной функции, физический и геометрический смысл производной. Уравнение касательной к графику функции. Производные суммы, разности, произведения, частного. Производные основных элементарных функций. Применение производной к исследованию функций и построению графиков. Производные обратной функции и композиции данной функции с линейной. Примеры использования производной для нахождения наилучшего решения в прикладных, в том числе социально-экономических, задачах. Нахождение скорости для процесса, заданного формулой или графиком. Вторая производная и ее физический смысл.
4 Модуль. Первообразная и интеграл (15 часов).
Понятие об определенном интеграле как площади криволинейной трапеции. Первообразная. Формула Ньютона-Лейбница. Примеры применения интеграла в физике и геометрии.
7 Модуль. Уравнения и неравенства (72 часа).
Основные приемы решения систем уравнений: подстановка, алгебраическое сложение, введение новых переменных. Равносильность уравнений, неравенств, систем. Решение уравнений, содержащих переменную под знаком модуля. Решение простейших систем уравнений с двумя неизвестными. Решение систем уравнений, содержащих переменную под знаком модуля. Решение систем неравенств с одной переменной. Использование свойств и графиков функций при решении уравнений и неравенств. Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем. Применение математических методов для решения содержательных задач из различных областей науки и практики. Интерпретация результата, учет реальных ограничений.
8 Модуль. Комплексные числа (10 часов).
Понятие комплексного числа. Алгебраическая форма, тригонометрическая форма, показательная форма комплексного числа. Сопряжённые комплексные числа. Геометрическая интерпретация комплексного числа. Корни комплексных чисел. Корни многочленов.
10 Модуль. Повторение курса алгебры и математического анализа (21 час).
II Блок Геометрия
1 Модуль. Метод координат в пространстве (21 часов).
Координаты и векторы. Декартовы координаты в пространстве. Формула расстояния между двумя точками. Уравнения сферы и плоскости. Формула расстояния от точки до плоскости. Векторы. Угол между векторами. Координаты вектора. Скалярное произведение векторов. Длина вектора в координатах, угол между векторами в координатах. Коллинеарные векторы, условие коллинеарности векторов в координатах.
5 Модуль. Цилиндр, конус, шар. (16 часов).
Цилиндр и конус. Усеченный конус. Основание, высота, боковая поверхность, образующая, развертка. Осевые сечения и сечения параллельные основанию. Шар и сфера, их сечения, касательная плоскость к сфере. Вписанные и описанные многогранники. Комбинации круглых тел. Геометрия окружности.
6 Модуль. Объемы тел (17 часов).
Понятие об объеме тела. Отношение объемов подобных тел. Формулы объема куба, прямоугольного параллелепипеда, призмы, цилиндра. Формулы объема пирамиды и конуса. Формулы площади поверхностей цилиндра и конуса. Формулы объема шара и площади сферы.
9 Модуль. Заключительное повторение (14 часов).
Личностные, метапредметные и предметные результаты освоения конкретного учебного предмета, курса
В результате изучения математики на базовом уровне ученик должен
знать (понимать)
значение математической науки для решения задач, возникающих в теории и практике; широту и в то же время ограниченность применения математических методов к анализу и исследованию процессов и явлений в природе и обществе;
значение практики и вопросов, возникающих в самой математике для формирования и развития математической науки; историю развития понятия числа, создания математического анализа, возникновения и развития геометрии;
универсальный характер законов логики математических рассуждений, их применимость во всех областях человеческой деятельности;
вероятностный характер различных процессов окружающего мира.
Алгебра
уметь
выполнять арифметические действия, сочетая устные и письменные приемы, применение вычислительных устройств; находить значения корня натуральной степени, степени с рациональным показателем, логарифма, используя при необходимости вычислительные устройства; пользоваться оценкой и прикидкой при практических расчетах;
проводить по известным формулам и правилам преобразования буквенных выражений, включающих степени, радикалы, логарифмы и тригонометрические функции;
вычислять значения числовых и буквенных выражений, осуществляя необходимые подстановки и преобразования;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
практических расчетов по формулам, включая формулы, содержащие степени, радикалы, логарифмы и тригонометрические функции, используя при необходимости справочные материалы и простейшие вычислительные устройства.
Функции и графики
уметь
определять значение функции по значению аргумента при различных способах задания функции;
строить графики изученных функций;
описывать по графику и в простейших случаях по формуле поведение и свойства функций, находить по графику функции наибольшие и наименьшие значения;
решать уравнения, простейшие системы уравнений, используя свойства функций и их графиков;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
описания с помощью функций различных зависимостей, представления их графически, интерпретации графиков.
Начала математического анализа
уметь
вычислять производные и первообразные элементарных функций, используя справочные материалы;
исследовать в простейших случаях функции на монотонность, находить наибольшие и наименьшие значения функций, строить графики многочленов и простейших рациональных функций с использованием аппарата математического анализа;
вычислять в простейших случаях площади с использованием первообразной;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
решения прикладных задач, в том числе социально-экономических и физических, на наибольшие и наименьшие значения, на нахождение скорости и ускорения.
Уравнения и неравенства
уметь
решать рациональные, показательные и логарифмические уравнения и неравенства, простейшие иррациональные и тригонометрические уравнения, их системы;
составлять уравнения и неравенства по условию задачи;
использовать для приближенного решения уравнений и неравенств графический метод;
изображать на координатной плоскости множества решений простейших уравнений и их систем;
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
построения и исследования простейших математических моделей.
Геометрия
уметь
распознавать на чертежах и моделях пространственные формы; соотносить трехмерные объекты с их описаниями, изображениями;
описывать взаимное расположение прямых и плоскостей в пространстве, аргументировать свои суждения об этом расположении;
анализировать в простейших случаях взаимное расположение объектов в пространстве;
изображать основные многогранники и круглые тела; выполнять чертежи по условиям задач;
строить простейшие сечения куба, призмы, пирамиды;
решать планиметрические и простейшие стереометрические задачи на нахождение геометрических величин (длин, углов, площадей, объемов);
использовать при решении стереометрических задач планиметрические факты и методы;
проводить доказательные рассуждения в ходе решения задач.
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
исследования (моделирования) несложных практических ситуаций на основе изученных формул и свойств фигур;
вычисления объемов и площадей поверхностей пространственных тел при решении практических задач, используя при необходимости справочники и вычислительные устройства.
Диагностика результатов обучения проводится в виде теоретических зачётов, многовариантных самостоятельных, контрольных работ, материалы для которых взяты из заданий открытого банка заданий ЕГЭ.
Учебно-методический комплект
1. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин – М.: Просвещение, 2010г «Алгебра и начала анализа 10».
2. С.М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин – М.: Просвещение, 2010г «Алгебра и начала анализа 11».
3. Атанасян Л. С. «Геометрия 10-11».
4. Симонов А. Я. «Система тренировочных задач и упражнений по математике».
5. Дорофеев Г. В. «Сборник заданий для проведения письменного экзамена по математике за курс средней школы».
6. Сканави М.И. «Сборник задач по математике для поступающих во Втузы».
7.М.К.Потапов А.В.Шевкин«Дидактические материалы по алгебре»(10,11классы).
8. Тесты ЕГЭ различных лет.
Календарно-тематическое (поурочное) планирование
по геометрии (профильный уровень)
на 2012-2013 учебный год
Класс: 11
Всего часов: 238 (7 часа в неделю)
№ урока
|
к-во часов
|
Дата
План
|
Тема урока
|
Тип урока
|
Элементы содержания Деятельность учащихся
|
Повторение
|
Форма
контроля
|
Дидактические
материалы,
наглядные пособия,
средства ИКТ
|
|
6 ч
|
Векторы в пространстве
|
1
|
1
|
|
Понятие вектора в пространстве
|
Комбинированный
|
Знать основные понятия и определения темы; уметь решать задачи на пространственных чертежах
|
Основные понятия темы «Векторы на плоскости»
|
Фронтальный опрос
Взаимопроверка
Индивид. контроль
|
|
2
|
1
|
|
Сложение и вычитание векторов. Умножение вектора на число
|
Комбинированный
|
Знать правила и свойства сложения и вычитания векторов, умножения вектора на число; уметь выполнять действия над векторами
|
Правила сложения, вычитания и умножения на число векторов на плоскости
|
Фронтальный опрос
Взаимопроверка (работа в парах)
Индивид. контроль
|
Проектор (демонстрационный материал для решения задач по готовым чертежам)
|
3
|
1
|
|
Сложение и вычитание векторов. Умножение вектора на число
|
Урок формирования ЗУН
|
Уметь решать задачи на применение правил и свойства сложения и вычитания векторов, умножения вектора на число
|
Сумма нескольких векторов на плоскости
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Проектор (демонстрационный материал для решения задач по готовым чертежам)
|
|
4
|
1
|
|
Компланарные векторы. Правило параллелепипеда
|
Комбинированный
|
Знать определение компланарных векторов; правило параллелепипеда; формировать умение решать задачи с помощью чертежей пространственных фигур
|
Правила действий над векторами
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
Матем. диктант
|
Дидактический материал (карточки для индивид. и групповой работы)
|
|
5
|
1
|
|
Разложение вектора по трем некомпланарным векторам
|
Комбинированный
|
Уметь решать задачи на применение теоремы о разложении вектора по трем некомпланарным векторам
|
|
Фронтальный опрос
Взаимопроверка (работа в парах)
Индивид. контроль
|
Дидактический материал (карточки для индивид. и групповой работы)
|
|
6
|
1
|
|
Векторы в пространстве: зачет №1
|
Урок проверки знаний
|
Знать основные определения, правила и свойства действий над векторами; уметь решать задачи базового и повышенного уровней
|
Основные определения и теоремы темы «Векторы в пространстве»
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
Дидактический материал (карточки для индивид. работы)
|
|
Итого: 6 уроков
|
15 ч
|
Метод координат в пространстве
|
7
|
1
|
|
Прямоугольная система координат в пространстве. Координаты точки
|
Комбинированный
|
Уметь выполнять построение точек с заданными координатами в пространстве; решать задачи на нахождение координат точек в системе координат в пространстве
|
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Проектор (демонстрационный материал для решения задач по готовым чертежам)
|
|
8
|
1
|
|
Координаты вектора
|
Комбинированный
|
Знать правила сложения, вычитания и умножения на число векторов в координатной форме; уметь решать задачи на вычисление координат суммы и разности векторов, произведения вектора на число
|
Координаты вектора, действия с векторами в координатной форме на плоскости
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
|
|
9
|
1
|
|
Связь между координатами векторов и координатами точек
|
Комбинированный
|
Формировать умение решать задачи на действия с векторами в координатной форме
|
Понятие радиус-вектора и его координат на плоскости
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
Дидактический материал (карточки для инд. работы)
|
|
10
|
1
|
|
Простейшие задачи в координатах
|
Комбинированный
|
Знать формулы координат середины отрезка, длины вектора и расстояния между двумя точками и уметь применять их при решении задач
|
Основные задачи в координатах на плоскости
|
|
|
|
11
|
1
|
|
Простейшие задачи в координатах
|
Урок формирования ЗУН
|
Формировать умение решать задачи повышенного уровня на применение основных формул в координатной форме
|
Алгоритмы простейших задач в координатах
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Дидактический материал (карточки для инд. работы)
|
|
12
|
1
|
|
Простейшие задачи в координатах
|
Комбинированный
|
Формировать умение решать задачи повышенного уровня на применение основных формул в координатной форме
|
|
Фронтальный опрос
Индивид. контроль
Матем. диктант
|
Дидактический материал
|
|
13
|
1
|
|
Угол между векторами. Скалярное произведение векторов
|
Урок изучения нового материала
|
Формировать понятие угла между векторами и скалярного произведения векторов в пространстве; умение решать задачи на базовом уровне
|
Угол между векторами и скалярное произведение векторов на плоскости; условие перпендикулярности двух векторов
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
|
|
14
|
1
|
|
Скалярное произведение векторов
|
Комбинированный
|
Формировать умение решать задачи повышенного уровня на применение определения и свойств скалярного произведения векторов
|
Свойства скалярного произведения векторов
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
Проектор (демонстрационный материал для решения задач по готовым чертежам)
|
|
15
|
1
|
|
Вычисление углов между прямыми и плоскостями
|
Комбинированный
|
Формировать понятие направляющего вектора прямой, угла между прямыми и плоскостями; умение решать задачи на вычисление углов между прямыми и плоскостями
|
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
|
|
16
|
1
|
|
Уравнение плоскости
|
Комбинированный
|
Формировать умение решать задачи на применение уравнения плоскости для вычисления расстояния от данной точки до плоскости
|
Уравнение прямой на плоскости
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
|
|
17
|
1
|
|
Движения. Симметрия
|
Комбинированный
|
Формировать понятие движения пространства; центральной, осевой и зеркальной симметрии в пространстве; формировать умение решать задачи на доказательство по теме «Движения»
|
Понятие отображения плоскости на себя, преобразования движения, его виды и свойства
|
Взаиморецензирование домашних работ
Фронтальный опрос
Индивид. контроль
|
|
|
18
|
1
|
|
Параллельный перенос. Подобие
|
Комбинированный
|
Формировать понятие параллельного переноса и подобия в пространстве; умение решать задачи на доказательство по теме «Движения»
|
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Проектор (демонстрация электронного плаката «Движения»)
|
|
19
|
1
|
|
Задачи в координатах
|
Урок закрепления и коррекции ЗУН
|
Формировать умение решать задачи вычислительные и на доказательство на базовом и повышенном уровнях
|
Основные понятия и формулы темы «Метод координат в пространстве»
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Дидактический материал (карточки для инд. работы)
|
|
20
|
1
|
|
Метод координат в пространстве:
зачет №2
|
Урок проверки знаний
|
Знать основные понятия, теоремы и формулы темы.
Применять ЗУН при решении задач
|
Основные определения и теоремы темы «Метод координат в пространстве»
|
Индивид. контроль
Взаимопроверка
|
Дидактический материал (карточки для индивид. и групповой работы)
|
|
21
|
1
|
|
Контрольная работа № 1
|
Урок проверки знаний и умений
|
Применять ЗУН при самостоятельном решении задач
|
|
Письменный обобщающий контроль
|
Дидактический материал
|
|
11 ч Функции и их графики.
|
22
|
1
|
|
Элементарные функции
|
Урок обобщения и систематизации изученного
|
Элементарные функции
|
Функции изученные в 7-10 кл
|
Индивид. контроль
Взаимопроверка
|
Дидактический материал
|
|
23
|
1
|
|
Область определения и область изменения функции. Ограниченность функции.
|
Урок обобщения и систематизации изученного
|
Вспомнить область определения и область значения функции. Дать понятие ограниченности функции.
|
Область определения , область значения
|
Индивид. контроль
Взаимопроверка
|
Дидактический материал
|
|
24-25
|
2
|
|
Чётность, нечётность, периодичность функции
|
Урок обобщения и систематизации изученного
|
Рассмотреть чётность и нечётность и периодичность функции
|
Чётность и нечётность и периодичность функции
|
Письменный обобщающий контроль
|
Дидактический материал (карточки для инд. работы)
|
|
26-27
|
2
|
|
Промежутки возрастания, убывания, знакопостоянства и нули функции.
|
Комбинированный
|
Находить промежутки возрастания, убывания, знакопостянства функции.
|
Промежутки возрастания, убывания, знакопостянства функции.
|
Фронтальный опрос
Индивид. контроль
Взаимопроверка
|
Дидактический материал
|
|
28
|
1
|
|
Исследование функций и построение графиков элементарными методами.
|
Комбинированный
|
Исследование функции по схеме.
|
Свойства функций
|
Письменный обобщающий контроль
|
Дидактический материал (карточки для инд. работы)
|
|
29-30
|
2
|
|
Основные способы преобразования графиков.
|
Комбинированный
|
Уметь преобразовывать графики функций
|
Преобразование графиков.
|
Индивид. контроль
Взаимопроверка
|
Дидактический материал
|
|
31
|
1
|
|
Графики функций, содержащих модули.
|
Урок формирования ЗУН
|
Уметь строить графики содержащие модуль
|
|
Письменный обобщающий контроль
|
Дидактический материал
|
| |
|
|
 Скачать 0.93 Mb.
Скачать 0.93 Mb.