Разработка урока конференции по геометрии и информатике «Известная и неизвестная прямоугольная система координат» (городской семинар учителей математики) Разработали: Хабибулина Л. В
 Скачать 145.32 Kb. Скачать 145.32 Kb.
|
| Отдел образования акимата города Тараз Коммунальное государственное учреждение «Средняя школа № 2» Разработка урока – конференции по геометрии и информатике «Известная и неизвестная прямоугольная система координат» (городской семинар учителей математики) Разработали: Хабибулина Л.В., учитель математики высшей категории, Бекбасарова Ж.А., учитель информатики первой категории г. Тараз -2013 год Урок научно-практическая конференция Тема: «Известная и неизвестная прямоугольная система координат» (Слайд № 1) Цель: 1) обучающая: формирование понятий о декартовой системе координат в пространстве и об использовании метода координат при решении задач; 2) развивающая: развитие умений анализировать, сравнивать, делать выводы; развитие; развитие исследовательских умений и навыков; 3) воспитательная: воспитание творческого отношения к учебной деятельности, ответственного отношения к обучению. Тип урока: урок изучения нового материала Вид урока: урок-конференция Формы урока: групповая работа; коллективная Методы урока: информационно-поисковые; наглядно-образные; метод проектов Оборудование: презентация к уроку «Известная и неизвестная прямоугольная система координат», творческие проекты учащихся, сопроводительные карты по информатике; ПК, ИАД. Межпредметные связи: география, алгебра, информатика, история, литература Прогнозируемый результат: 1) уметь оперировать понятиями: прямоугольная система координат в пространстве, метод координат; 2) уметь использовать формулы расстояния между двумя точкам в пространстве и координат середины отрезка при решении базовых задач и тестовых заданий; 3) уметь использовать алгоритм построения точек по заданным координатам при построении поверхностей, биоритмов человека. План урока: I. Организация начала урока – 3 минуты Сообщение темы, целей урока. Эпиграф урока II. Мотивация учебной деятельности – 5 минут Вводная беседа; представление «участников» конференции, тем проектов. III. Изучение нового материала – 45 минут Защита творческих проектов секций лингвистики, истории, математики, прикладной математики; построение поверхностей в декартовой системе координат; комментарий к проектам учащихся учителей математики и информатики. IV. Формирование первичных умений и навыков – 17 минут Решение задач VI. Историческая справка – 15 минут Защита творческих проектов секции искусствоведения, отдела практики; построение биоритмов человека; комментарий к проектам учащихся учителей математики и информатики. VII. Подведение итогов урока – 3 минуты Выводы по уроку; составление буклета «Известная и неизвестная прямоугольная система координат». VIII. Домашнее задание – 2 минуты Комментарий к выполнению домашнего задания. Ход урока: I. Организация начала урока (Слайд № 2) Учитель математики Тем, кто любит математику, Тем, кто знает математику, Тем, кто ещё не знает, Что он любит математику И тем, кто других учит математике Предназначена эта научно-практическая конференция «Известная и неизвестная прямоугольная система координат». Эпиграфом сегодняшнего урока могут стать слова П. Лапласа, который сказал: «То, что мы знаем – ограничено, а то, что мы не знаем – бесконечно…» (Слайд № 3) II. Мотивация учебной деятельности (вводная беседа) Учитель математики У каждого человека бывают ситуации, когда необходимо определить свое или чьё-то местонахождение, к примеру найти по билету место в зрительном зале или в вагоне поезда, определить местонахождение того или иного здания, дома, квартиры. Мы нередко можем слышать такую фразу «Оставьте мне ваши координаты» Что означает это выражение для простого человека и для математика? Догадались?! На первый взгляд ваш собеседник просит у вас либо адрес, либо номер телефона. А с точки зрения математики вас просят указать координаты некоторой точки. Суть координат, или системы координат состоит в том, что они позволяют без особого труда определить положение точки в плоскости, в пространстве. И не только. Где же мы можем ещё встретить координаты помимо математики?
Об этом и многом другом интересном сегодня мы и будем говорить. Заявку на участие в работе научно-практической конференции подали следующие секции, подготовившие такие темы: (Слайд № 4) Учитель математики
Ну что же, цель поставлена, и наша задача сегодня, достигнуть поставленную цель. III. Изучение нового материала. (Слайд № 5) Учитель математики Первое определение IX книги «Начала» Евклида гласит: «Тело есть то, что имеет длину, ширину и глубину». Тем не менее, есть основание полагать, что в древности такого современного понятия о трехмерном пространстве как оно есть сейчас, не существовало. Уже у Декарта имелись лишь далекие намеки на возможность распространения метода координат с двумерного пространства (плоскости) на трехмерное пространство. Однако потребовалось ещё почти 100 лет, чтобы идея пространственных координат была сформирована, постоянно и широко использовалась. 1) У каждого исследователя бывает такое желание, прежде чем приступить к изучению темы, хочется узнать толкование и происхождение тех слов, которые используются в изучаемой теории. Поэтому первыми свою работу представят ребята из секции лингвистов, которые нам расскажут о происхождении слов, связанными с декартовыми координатами. (выступление секции лингвистики) (Слайд № 6) 2) Учитель математики История возникновения координат и системы координат начинается давно, первоначально идея метода координат возникла ещё в древнем мире в связи с потребностями астрономии, географии, живописи. Изображать числа в виде точек, а точкам давать числовые обозначения было желанием ещё античной геометрии, связанное с потребностью сопоставлять положение светил на небе и определенных пунктов на поверхности Земли. О том, какова же история появления теории системы координат, расскажут нам представители секции истории. (выступление секции истории) 3) Учитель математики Что собой представляет система координат в пространстве? И почему их такое неимоверное множество? Неужели нельзя придумать одну универсальную систему и везде ее использовать? Оказывается нельзя. И сегодня мы разберемся почему. Что такое система координат? Система координат – это способ задания положения точек в пространстве, а образуют систему координат три взаимно перпендикулярные прямые, пересекающиеся в одной точке. ( 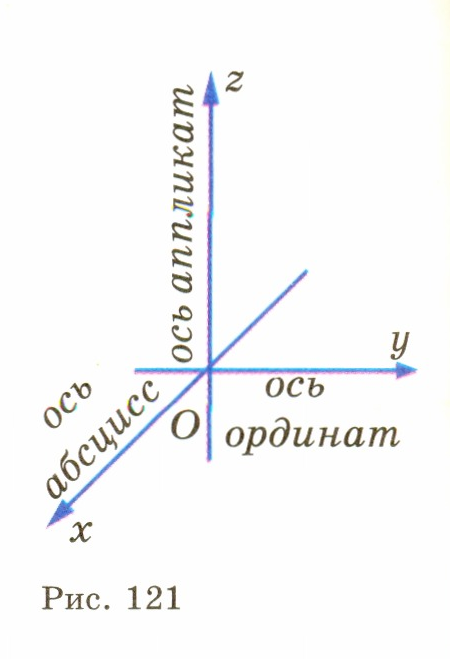 Слайд № 7) Слайд № 7)Высь, ширь, глубь. Лишь три координаты. Мимо них, где путь? Засов закрыт. С Пифагором слушай сфер сонаты, Атомам дли счёт, как Демокрит. В. Брюсов.   Главное свойство всех систем координат то, что положение любой точки однозначно определяется ее координатами. Так же как по адресу можно найти лишь одно здание в пределах города. Кроме прямоугольных систем координат существует целый ряд других систем. Иногда на плоскости и в пространстве используют и другие системы координат. О многообразии систем координат и о том, что с ними связано, расскажут ребята из секции математики. (выступление секции математики) Учитель информатики Пояснения: 1) построение точки в пространстве по заданным координатам; 2) определение координат данной точки в пространстве; (использование презентации) 3) построение поверхностей в декартовой системе координат (использование слайдов, сопроводительных карт) (Слайд № 8) Учитель математики Говоря о математике как науке нельзя ещё раз не вспомнить слова великого Рене Декарта «Математика – мощный и универсальный метод познания природы, образец для других наук». 4) Идеей применить к решению многих алгебраических задач теорию координат интересовались многие математики, однако впервые её смогли применить Рене Декарт и Пьер Ферма. (Слайд № 9) Учитель математики В 1637 г. во Франции вышла книга, которая принесла её автору невероятную известность. По обычаям того времени она имела довольно длинное название: «Рассуждение о методе, позволяющем направлять разум и отыскивать истину в науках. Кроме того, Диоптрика, Метеоры и Геометрия, которые являются приложениями этого метода». Автор книги был Рене Декарт. В ней он не только ввел прямоугольную систему координат, поставил каждой точке в соответствие пару чисел – её координаты, но и продемонстрировал возможность решения геометрических задач иным, алгебраическим способом. Этот прогрессивный метод оказалось очень удобным, т.к. метод координат, позволил переходить от точки к паре чисел, от линии к уравнению, от геометрии к алгебре. (Слайд №9 «А») Учитель математики Первые строки книги «Рассуждение о методе…» были такие слова Декарта: «Я мыслю, следовательно, я существую». Так Рене Декарт попытался заявить миру о своей новой теории. Подробно о методе координат и его применении к решению задач нам расскажут представители секции прикладной математики в своей творческой работе «Метод координат и его применение к решению задач» (выступление секции прикладной математики) (Слайд № 10) Учитель математики Вклад в развитие координатного метода внес также Пьер Ферма, однако его работы были впервые опубликованы уже после его смерти. И Декарт, и Ферма применяли координатный метод только на плоскости. Координатный метод для трёхмерного пространства впервые применил Леонард Эйлер уже в XVIII веке. IV. Формирование первичных умений и навыков. Учитель математики 1) Рассмотрим частные случаи расположения точек в пространстве. Как определить положение точки в пространстве? (Слайд № 11) - Назовите координаты точек, лежащих на координатных осях. Какие из данных точек лежат на координатных осях и на какой: А(5;0;0), В(-7;5;0), С(0;0;-9), М(0;8;0), Р(0;1;0)? - Назовите координаты точек, лежащих в координатных плоскостях. Какие из данных точек лежат в координатных плоскостях и в какой из плоскостей: А(3;0;5), В(-1; 4; 6), С(0;5;-9), М(5;5;0), Х(9;7;0)? - Назовите координаты точки, совпадающей с началом координат; лежащих в пространстве. Выбрать среди заданных точек те, которые лежат в пространстве или в начале координат: А(0;7;-2), О (0;0;0), В(2;4;-4), М(8;-5;2), Р(0;0;0). 2) Секция прикладной математики в своем проекте нас уже познакомила с основными принципами решением задач координатным методом. Рассмотрим решение ещё нескольких задач методом координат. (Слайд № 12) Задача. Письменно Дано: А (1;-1;2), В (3;1;-2) Найдите координаты середины отрезка АВ и его длину. Решение: 1). Пусть С – середина отрезка АВ, тогда С ( 2). АВ = Ответ: С (2;0;0), АВ = 2 3) Подготовка к ЕНТ (сб. тестов НЦТ 2009 год, В 3 № 24) Найти координаты центра тяжести треугольника с вершинами в точках А(3; -4; 7), В(-5; 3; -2) и С(8; 7; -8). А. (-2; -2; 1), В. (-5; 3; 9), С. (2; 2; 1), D. (2; 2; -1), Е. (2; -2; -1). Решение. (Слайд № 13) Из планиметрии мы знаем, что центр тяжести треугольника, указанного в условии задачи, находится в точке пересечения его медиан. Из элементарной геометрии известно, что три медианы треугольника пересекаются в одной точке, причем эта точка делит медианы в отношении 2:1, считая от вершины треугольника. Рассмотрим в координатной плоскости ∆АВС. Обозначим точку пересечения медиан (центр тяжести треугольника) буквой E, ее координаты - xE и yE . 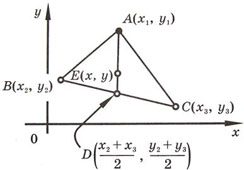 Координаты центра тяжести однородной треугольной пластинки, если не учитывать ее толщину, равны среднему арифметическому однородных координат ее вершин. Координаты центра тяжести треугольника, расположенного в пространстве будут находиться по формулам: ; ZЕ = Z1 + Z2 + Z3 3  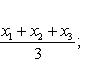 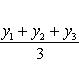 Возвращаясь к условию задачи, получим: Е (Хц; Уц; Zц) Хц = (3-5+8 ): 3 = 2 ; Уц = (-4+3+7) : 3 = 2 ; Zц = ( 7- 2 – 8) : 3 = -1 Е(2; 2; -1) – D. Задача . Самостоятельно (Слайд № 14) (сб. апробационных тестов НЦТ 2013 год, В 0173 № 24) Найти координаты центра тяжести треугольника с вершинами в точках А(7; -4), В(-1; 8) и С(-12; -1). А. (2; 1), В. (-2; 1), С. (3; -2), D. (-1; 2), Е. (2,5; 3). (Ответ: В(-2; 1) ). 4) Работа с учебником: решение задач № 4 стр. 68; дополнительно № 9 стр. 68 – комментирование у доски. VI. Историческая справка: Интересные факты. (Слайд № 15) Учитель математики Трудно переоценить значение декартовой системы координат в развитии математики и её приложений. Огромное количество задач, требовавших для решения геометрической интуиции, специфических методов получило решение, состоящее в аккуратном проведении алгебраических выкладок. Немалой заслугой Декарта было введение удобных обозначений, сохранившихся до наших дней: латинских букв x, y, z - для неизвестных; a, b, c - для коэффициентов, x2, y5, a7- для степеней. Основное новшество Декарта - введение переменных величин как координатных отрезков переменной длины. Идея геометрии Декарта состоит в том, что геометрический объект задается уравнением, связывающим переменные величины. По свойствам уравнения судят о свойствах геометрического объекта. Декарт считается одним из основателей новой математики – аналитической геометрии. Его имя сохранили термины: «декартовы координаты», «декартов лист», «правило знаков Декарта», «метод неопределенных коэффициентов Декарта». (Слайд № 16) Учитель математики Историческая справка. 1618 год. Прохожих мало. Молодой солдат в форме армии Морица Оранского со скучным видом ходит по мостовой. Цель - найти развлечение. Около одной из деревянных тумб с наклеенными объявлениями - толпа. Солдат прислушивается; на его лице досада - говорят на чисто голландском языке. Ясно одно, предмет разговора – лист бумаги, приклеенный к тумбе. «Что здесь написано?» - по-французски спрашивает молодой человек. Его не понимают. Один из тех, к кому обращается солдат, смотрит на француза с интересом и говорит, что переведет, но с условием, что солдат принесет ему решение всех этих задач, или хотя бы одной из них. Голландец представился французу как - преподаватель физики, медицины и математики - Бекман, а на плакате, сказал он, конкурс на решение задач. Решивший получит титул лучшего математика города. На следующее утро солдат постучал в дверь Бекмана. Еще ни не случалось, чтобы кто-нибудь сразу решил все задачи, над которыми ломали головы общепризнанные авторитеты. Этот француз, родом из Турени, воспитывался в иезуитской коллегии, там же изучал математику. А в будущем как оказалось, этот молодой француз заложил основы аналитической геометрии, дал понятие переменной величины и функции. Его именем названа алгебраическая кривая третьего порядка, а также прямоугольная система координат на плоскости и в пространстве. Догадались? Конечно, это Рене Декарт. Интересен тот факт, что Рене Декарт увлекался не только математикой как наукой. Он увлекался науками от медицины до метеорологии. Его многочисленные труды были посвящены философии, астрономии, психологии, физиологии, физике и другим наукам. Декарт первый математически вывел закон преломления света (независимо от В. Снеллиуса) на границе двух различных сред. Точная формулировка этого закона позволила усовершенствовать оптические приборы, которые тогда стали играть огромную роль в астрономии и навигации. Великий физиолог И. П. Павлов поставил памятник-бюст Рене Декарту возле своей лаборатории (Колтуши), потому что считал его предтечей своих исследований.  Можно ещё много говорить о славе этого ученого, но вполне уместным является вопрос: А есть ли такие области, где не используется наследие Рене Декарта? И, конечно же, простой обыватель может с уверенностью сказать: конечно – это же элементарно, искусство – вот та область, для которой имя Декарта осталось неизвестным. Однако вы поторопились! (Слайд № 17) Учитель математики И подтверждение тому можно найти в словах А. Принсгейма «В чистой математике живет всегда художник: архитектор и даже поэт». И, наверное, не зря заявку на участие в научно-практической конференции подали участники секции искусствоведов, которые работали по теме «Декартовы координаты в искусстве». ( выступление секции искусствоведов) (Слайд № 18, 19) Учитель математики Системы координат пронизывают всю практическую жизнь человека и находит свое применение почти в каждой специальности.. Вы скажете что этого не может быть. Вот изучили систему координат на уроках геометрии и все на этом. Однако это не так. И именно с этим вопросом обратимся к отделу практики, который раскроет нам тайны тех профессий, использующих в своей работе теорию о системе координат. (выступление отдела практики) Учитель информатики: 1) объясняет последовательность построения биоритмов человека; 2) совместно с «отделом практики» выполняет построение эмоционального, интеллектуального и физического биоритмов аудитории. (использование слайдов, ПК) VII. Подведение итогов урока. Учитель математики - Что узнали нового на уроке? (ответы учащихся) Вопросы и задачи по теме: (Слайд № 20) - Объясните, как определяются координаты точки в пространстве. - У каждой ли точки пространства можно определить координаты? - Сколько для этого потребуется чисел? - Каким свойством обладают координаты точек, лежащих на координатных осях? - Каким свойством обладают координаты точек, лежащих в координатных плоскостях? - Даны точки: А(-3; 0; 0), В(5; 0; -1), С(0; 0; 8), D (-1;5;0), Е(0; 7;4), F(-6;-1; 0), К(0;0;0), М(0;-3;5), N(2;4;-1), Р(0;-6;0). Определите точки, принадлежащие: а) осям координат х, у, z; б) координатным плоскостям ху, хz, уz. Закончить сегодняшнюю научно-практическую конференцию «Известная и неизвестная прямоугольная система координат» словами Омара Хайяма «Изучив столько всего, лишь теперь, уразумел я, что на самом деле не знаю ничего…» (Слайд № 21) - Как выдумаете, почему именно эти строки завершают сегодняшний урок? (выступления учащихся, выводы по уроку) VIII. Домашнее задание: (Слайд № 22) §19, § 20, теория, составить кластер по теме (работа в группах), № 4, №5 стр. 66; № 1, № 3 стр. 68 |