Рабочая программа по алгебре 8 класс б 136 часов составитель: учитель математики Вахрушева Е. В. Ижевск 2010г. Пояснительная записка
 Скачать 306.75 Kb. Скачать 306.75 Kb.
|
| Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 89 с углубленным изучением отдельных предметов» Обсуждена на заседании методического объединения «___»___________2010г. Рассмотрена на заседании НМС «___»___________2010г. Утверждена директором школы «___»___________2010г. РАБОЧАЯ ПРОГРАММА ПО АЛГЕБРЕ 8 КЛАСС Б 136 ЧАСОВ Составитель: учитель математики Вахрушева Е.В. Ижевск 2010г. Пояснительная записка Материалы для рабочей программы составлены на основе:
Данная рабочая программа рассчитана на учащихся 8 физико-математического класса и предполагает базовый (продвинутый) уровень изучения предмета. Преподавание ведется по учебнику Учебник «Алгебра, 8» Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова. На изучение курса отводится 4 часа в неделю, всего 136 часов в год. Федеральный компонент государственного образовательного стандарта основного общего образования по математике Изучение математики в основной школе направлено на достижения следующих целей: – овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования; – развитие таких качеств личности, как ясность и точность мысли, логическое мышление, пространственное воображение, алгоритмическая культура, интуиция, критичность и самокритичность; – формирование представлений об идеях и методах математики как универсального языка науки и техники, средстве моделирования процессов и явлений; – формирование средствами математики культуры личности, знакомство с жизнью и деятельностью видных отечественных и зарубежных ученых-математиков, понимание значимости математики для общественного прогресса. Алгебра Алгебраические выражения. Буквенные выражения (выражения с переменными). Допустимые значения переменных, входящих в алгебраические выражения. Числовое значение буквенного выражения. Свойства степеней с целым показателем и их применение в преобразовании выражений. Многочлены. Сложение, вычитание, умножение многочленов. Формулы сокращенного умножения: квадрат суммы и квадрат разности, куб суммы и куб разности. Формула разности квадратов, формула суммы кубов и разности кубов. Разложение многочлена на множители. Вычисления значений арифметических и алгебраических выражений. Уравнения и неравенства. Уравнение с одним неизвестным. Корень уравнения. Линейное уравнение. Система уравнений. Решение системы. Система двух линейных уравнений с двумя неизвестными. Методы подстановки и алгебраического сложения. Составление уравнений и их систем по условиям задач. Решение текстовых задач алгебраическим методом. Числовые Функции. Понятие функции. Область определения функции. Способы задания функции. График функции, возрастание и убывание функции, наибольшее и наименьшее значения функции. Прямая пропорциональность, линейная функция и ее график, геометрический смысл коэффициентов. Использование графиков функций для решения уравнений и систем. Использование преобразований графиков (параллельный перенос вдоль осей координат и симметрия относительно осей). Требования к уровню подготовки выпускников (для учащихся 8-го класса) В результате изучения математики ученик должен знать/понимать*
АРИФМЕТИКА уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
АЛГЕБРА уметь
использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
ЭЛЕМЕНТЫ ЛОГИКИ, КОМБИНАТОРИКИ, СТАТИСТИКИ И ТЕОРИИ ВЕРОЯТНОСТЕЙ уметь
• находить частоту события, используя собственные наблюдения и готовые статистические данные; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
Общеучебные умения и навыки
– ставить цели самообразовательной деятельности – самостоятельно оценивать деятельность посредством сравнения с существующими требованиями – планировать свою деятельность в соответствии с поставленными целями и задачами – вносить изменения в последовательность и содержание учебных задач
– владеть различными видами изложения текста – владеть навыком аналитического чтения текста – составлять доклады и рефераты – планировать и проводить наблюдение за объектом – составлять программы эксперимента – составлять модели изучаемого объекта
– определять аспект анализа (точку зрения) – определять соотношения компонентов объекта – выполнять полное комплексное сравнение – классифицировать по нескольким признакам – выбирать форму доказательства( прямое, косвенное) – опровергать выдвинутую гипотезу – определять проблему и предлагать способы ее решения
– придерживаться определенного стиля при выступлении – выступать перед аудиторией – владеть языком науки, лежащей в основе учебного предмета Умения и навыки
В результате изучения курса математики учащиеся должны: – Осознать, что развитие понятия числа, введение в математику новых чисел обусловлено потребностями практики, а также внутренними потребностями математики; ознакомиться с историческими сведениями о возникновении и развитии чисел; на примере десятичной системы счисления и римской нумерации получить представление о позиционной и непозиционной системах записи чисел; – научиться рационализировать вычисления; при нахождении значений выражений эффективно сочетать устные, письменные вычисления и применение калькулятора; приобрести привычку контролировать вычисления, выбирая подходящий по ситуации способ (прикидкой, выполнением обратных действий, проверкой на правдоподобие результата и пр.); – овладеть понятиями и умениями, связанными с приближенными вычислениями; овладеть приемами прикидки и оценки результатов вычислений. – правильно употреблять термины, связанные с различными видами чисел и способами их записи: целое, дробное, рациональное, десятичная дробь; – уметь сравнивать два числа, упорядочивать в несложных случаях наборы чисел, понимать связь отношений «больше», «меньше» с расположением точек на координатной прямой, изображать числа на координатной прямой; – выполнять арифметические действия с рациональными числами, находить значения степеней и квадратных корней; сочетать при вычислениях устные и письменные приемы; - составлять и решать пропорции, решать основные задачи на дроби, проценты.
В результате изучения курса математики учащиеся должны: - правильно употреблять термины «выражение», «тождественное преобразование», понимать их в тексте, в речи учителя, понимать формулировку заданий: «упростить выражение», «разложить на множители»; - составлять несложные буквенные выражения и формулы; осуществлять в выражениях и формулах числовые подстановки и выполнять соответствующие вычисления; выражать из формул одни переменные через другие; - выполнять действия со степенями с натуральным и целым показателями, многочленами, алгебраическими дробями; выполнять разложение многочленов на множители вынесением общего множителя за скобки, применением формул сокращенного умножения; - выполнять преобразования числовых выражений, содержащих квадратные корни.
В результате изучения курса математики учащиеся должны: – получить представления об уравнениях как математическом аппарате решения разнообразных задач из математики, смежных областей знаний, практики; – правильно употреблять термины «уравнение», «неравенство», «система», «корень уравнения», «решение системы», понимать их в тексте, в речи учителя, понимать формулировку задачи «решить уравнение, неравенство, систему»; - решать линейные, квадратные уравнения и простейшие рациональные уравнения, сводящиеся к ним, системы уравнений с двумя переменными (линейные и системы, в которых одно урввнение второй степени); - решать линейные уравнения с одной переменной и их системы, неравенства второй степени; - решать текстовые задачи с помощью составления уравнений.
В результате изучения курса математики учащиеся должны: - понимать, что функция – это математическая модель, позволяющая описывать и изучать разнообразные зависимости между реальными величинами, что конкретные типы функций (прямая и обратная пропорциональности, линейная, квадратичная функции) описывают большое разнообразие реальных зависимостей; - правильно употреблять функциональную терминологию (значение функции, аргумент, график функции, область определения, возрастание и т.д.), понимать ее в тексте, в речи учителя, в формулировке задач; - находить значения функций, заданных формулой, таблицей, графиком; решать обратную задачу; - находить по графику функции промежутки возрастания и убывания функции, промежутки знакопостоянства, наибольшее и наименьшее значения; - строить графики линейной функции, прямой и обратной пропорциональности, квадратичной функции. УЧЕБНО-МЕТОДИЧЕСКИЙ КОМПЛЕКТ
Предлагаемый сборник предназначается для проверки в тесто вой форме уровня усвоения учащимися 8-го класса знаний и уме ний по математике в объеме, установленном обязательным мини мумом содержания образования. Пособие ориентировано на учеб ник «Алгебра, 8» (авторы: Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова). Оно также может быть полезно учителям и учащимся, занимающимся по другим учебникам. В сборник вклю чены тестовые задания различных типов, которые по форме соот ветствуют заданиям, использующимся в настоящее время как при итоговой аттестации за основную школу, так и в едином государ ственном экзамене. Сборник содержит 19 тематических тестов (по два равноценных варианта на каждую тему) и 2 варианта итоговых тестов. Тематические тесты предназначены для экспресс-анализа уров ня усвоения учащимися определенного раздела (темы). Они могут использоваться как средство обучения или контроля. Вариант тематического теста содержит 6 заданий. В сборник включены тематические тесты нескольких типов. Ва риант теста первого типа состоит из двух частей: - часть А содержит пять заданий с выбором одного верного ответа из четырех; - часть В содержит одно задание с кратким ответом. Выполнение теста первого типа рассчитано на 15-20 минут. Вариант тематического теста второго типа состоит из трех частей: -часть А содержит четыре (три) задания;
На выполнение теста второго типа отводится 25-30 или 30-40 минут, в зависимости от числа заданий с развернутым ответом. Особое положение в сборнике занимают тесты № 18, 19, на правленные на развитие графических представлений у восьмикласс ников. Они могут использоваться на факультативных занятиях по математике. Большинство заданий этих тестов повышенного (про фильного) уровня и предназначены учащимся, ориентированным на углубленное изучение предмета. Итоговое тестирование рекомендуется проводить в конце учеб ного года после итогового повторения всего курса алгебры 8-го класса. В итоговый тест не входит материал, который подлежит изу чению, но не включен в «Требования к уровню подготовки выпускни ков». Варианты итогового теста имеют следующую структуру: - часть А содержит тринадцать заданий; -часть В содержит три задания; -часть С содержит два задания. На выполнение итогового теста отводится 80 минут. Приложения 1 и 3 созданы в полном соответствии со «Стандар том основного общего образования по математике», утвержден ным приказом Минобразования России № 1089 от 5 марта 2004 г. В Приложении 1 представлен кодификатор, включающий те эле менты содержания из «Обязательного минимума содержания ос новных образовательных программ», которые изучаются в 8-ом классе. Ответы к заданиям и критерии оценивания части С приведены в приложении 5. Проверив решения учащихся, учитель проставляет суммарный балл за выполнение теста на бланке в соответствующей позиции. Рекомендации по использованию материалов сборника для учебного процесса В Приложении № 1 к данному сборнику дан кодификатор по курсу математики 8-го класса, соответствующий "Обязательному минимуму содержания основных образовательных программ", входящему в "Стандарт основного общего образования по математике", утвержденный приказом Минобразования России № 1089 от 5 марта 2004 г. В спецификации для итоговых тестов (Приложение № 2) указаны коды тем по этому кодификатору. Тематические тесты могут использоваться или как средство обучения или как средство контроля непосредственно после изучения соответствующей темы, а также при повторении пройденного материала. Итоговые тесты предназначены для установления уровня усвоения учащимися курса алгебры 8-го класса. Чтобы оценить результаты выполнения теста надо подсчитать суммарный тестовый балл. За каждое верно выполненное задание с выбором ответа (часть А) или задание с кратким ответом (часть В) выставляется по одному баллу. Количество баллов за каждое верно выполненное задание с развернутым ответом (часть С) в соответствии с предлагаемыми критериями оценивания ответа (Приложение № 5) составляет 1 -3 балла в зависимости от правильности метода решения, формы его записи и наличия или отсутствия ошибок в вычислениях. Успешность выполнения работы определяется в соответствии с нижеприведенными шкалами: для тематических тестов №: 1, 2, 3, 5, 6, 7, 8, 12, 13, 16 удовлетворительно - 4 (3-4) балла; хорошо - 5 баллов; отлично - 6 баллов; для тематических тестов (с заданием типа С) №: 4, 9, 10, 11,14,15,17 удовлетворительно - 4 балла; хорошо - 5-6 баллов; отлично - 7-8 баллов; для итоговых тестов: удовлетворительно -10-14 баллов; хорошо -15-18 баллов; отлично -19-22 баллов. Учитель может скорректировать предлагаемую шкалу оценок с учетом особенностей класса. Тесты № 18 и 19 представляют подборку заданий для тре нировки и не оцениваются по результатам выполнения. Комплект по математике обеспечивает усвоение обязательного минимума содержания и решает проблему преемственности математической подготовки между всеми ступенями обучения. Учебник оснащен методическими пособиями, дидактическими материалами. Самостоятельные работы являются обучающими и готовят учащихся к успешному выполнению контрольных работ. Задания контрольных работ соответствуют государственным стандартам по математике по программе 8 класса. Для каждой контрольной и самостоятельной работы учитель имеет возможность выработать свои критерии, по которым будет оцениваться работа, с учетом усвоения учащимися курса. Эти критерии должны соответствовать уровню усвоения знаний, умений и навыков, заложенному в государственной программе по математике. улы сокращенного умножения (23ители.ункции общего вида.учение математики на ступени основного общего образования отводится не Дополнительная литература:
Основные особенности предлагаемого сборника самостоятельных и контрольных работ: 1. Сборник содержит полный набор самостоятельных и конт рольных работ по всему курсу алгебры и геометрии 8 класса. Контрольные работы рассчитаны на один урок, самостоятель ные работы — на 20—35 минут, в зависимости от темы и уровня подготовки учащихся. 2. Сборник позволяет осуществить дифференцированный кон троль знаний, так как задания распределены по трем уровням сложности А, Б и В. Уровень А соответствует обязательным программным требованиям, Б — среднему уровню сложности, задания уровня В предназначены для учеников, проявляющих повышенный интерес к математике, а также для использования в классах, школах, гимназиях и лицеях с углубленным изучением математики. Учащиеся могут сравнить задания различных уровней и, с разрешения учителя, выбрать подходящий для себя уровень сложности. 3. В книгу включены домашние самостоятельные работы, содержащие творческие, нестандартные задачи по каждой изучае мой теме, а также задачи повышенной сложности. Эти задания могут в полном объеме или частично предлагаться учащимся в качестве зачетных, а также использоваться как дополнитель ные задания для проведения контрольных работ. По усмотре нию учителя выполнение нескольких или даже одного такого задания может оцениваться отличной оценкой. 4. Ответы к контрольным и домашним самостоятельным рабо там приводятся в конце книги. 5. Тематика и содержание работ охватывают требования дейст вующей программы по математике для 8 класса. Для удобства пользования книгой приводится таблица тематического распреде ления работ по учебникам Ю.Н.Макарычева и др., Ш. А. Али мова и др., А. В. Погорелова и Л. С. Атанасяна и др.
На выполнение работы отводится 80 мин. Работа состоит из двух частей и содержит 16 заданий. Часть1. На выполнение отводится 30 – 40 мин. Задания оцениваются в 1 балл. Часть2. На выполнение отводится 40 – 50 мин. Задания №1 - №5 оцениваются в 1 балла, задания №4 оценивается в 2 балла. Максимальное количество баллов за работу 23 балла. Перевод баллов в школьную оценку:
В данном пособии даны тесты трех типов: входной тест для 7 классов, промежуточные тесты, итоговые тесты для 7 классов. На выполнение теста отводится 60 мин, критерии оценивания для общего уровня До 11 баллов – «2» С 12 до 15 баллов – «3» С 16 до 18 баллов – «4» Свыше 19 баллов – «5».
Каждый тест является итоговой формой диагностики знаний учащихся при завершении изучения определенной темы курса. Содержат итоговый тест за курс 7 класса. Все работы представлены в 3 вариантах, каждый из которых содержит 10 задач, и отвечают как базовому минимуму, так и более высоким требованиям. Каждый тест требует выбора 1 правильного ответа из 5 предложенных. На выполнение теста отводится 40 мин, критерии оценивания для общего уровня До 4 баллов – «2» 5 баллов – «3» 6 до 7 баллов – «4» Свыше 8 баллов – «5».
Данное пособие представляет собой сборник тестов по алгебре для учащихся 8 класса. Книга ориентирована на учебник под редакцией С.А.Теляковского «Алгебра. 8 класс», но может быть использована и при обучении по другим учебным пособиям. По каждой теме, изучаемой в 8 классе, предлагается тест; некоторые темы разбиты на подтемы. Каждый тест представлен в 6 вариантах. Первые два из них достаточно просты и содержат задания на уровне обязательного минимума знаний, следующие два вари анта сложнее и предназначены для учащихся, хорошо усваивающих общеобразовательную программу. Вари анты 5—6 рассчитаны на сильных учащихся, учеников лицейских и математических классов. В каждом вари анте теста содержится 10 заданий, расположенных в по рядке увеличения сложности. Время выполнения теста может определить сам учитель; предполагается, что на 10 заданий будет отводиться один урок, но в, зависимости от уровня класса это время может быть увеличено. При необходимости учитель может разбить каждый вариант на 2 части по 5 заданий, в этом случае у него будет 12 различных вариантов теста по каждой теме. Задания из тестов можно использовать и для обычной контрольной, самостоятельной или проверочной работы.
Предлагаемое пособие предназначено для изучения и повто рения школьного курса математики за 7-10 классы, а также систематизации знаний учащихся и абитуриентов по данно му курсу. В пособии представлены следующие темы: «Рациональные дроби», «Степень числа с целым и дробным показателями», «Квадратные корни», «Квадратные уравнения», «Системы уравнений», «Неравенства», «Функции. Свойства и графики некоторых функций», «Уравнения и системы уравнений выс ших степеней», «Числовые последовательности», «Элементы тригонометрии». В соответствии с последовательностью изу чения предмета каждая тема разбита на подтемы, которые представлены тестами различных уровней. Задания тестов помогут усвоить или повторить все основ ные разделы темы, осуществить контроль и самоконтроль знаний. Начинать выполнение заданий лучше с теста первого уров ня, а заканчивать — тестом пятого уровня. При переходе от одного уровня к другому повышается сложность теста, уста навливаются связи с другими разделами курса математики. Задания пятого уровня соответствуют заданиям, предлагае мым на централизованном тестировании. Их краткие решения приведены в пособии. В конце каждой главы помещены тре нировочные задания для подготовки к централизованному тестированию и предлагаемые на вступительных экзаменах в вузы, а также их решения. Тесты будут полезны как абитуриентам при подготовке к конкурсным испытаниям, так и учителям и школьникам в процессе изучения соответствующего раздела школьного курса математики. интернет-ресурсы:
CD-диски
ТЕМАТИЧЕСКАОЕ ПЛАНИРОВАНИЕ УЧЕБНОГО МАТЕРИАЛА. «Алгебра, 8» Ю.Н. Макарычев (4ч в неделю, всего 136 ч) 1.Рациональные дроби (30ч)Рациональная дробь. Основное свойство дроби. Сложение, вычитание, умножение и деление алгебраических дробей. Преобразование алгебраических выражений. Функция вида у= 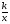 и ее график. и ее график.Основная цель – выработать умение выполнять тождественные преобразования рациональных выражений. 2.Квадратные корни (24ч)Понятие об иррациональном числе. Общие сведения о действительных числах. Квадратный корень, приближенное значение квадратного корня. Свойства квадратных корней. Преобразование выражений, содержащих квадратные корни. Функц ия 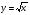 , ее свойства и график. , ее свойства и график.Основная цель – систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие числа; выработать умение выполнять простейшие преобразования выражений, содержащих квадратные корни. 3. Квадратные уравнения (28ч)Основные понятия, связанные с квадратными уравнениями. Формулы корней квадратного уравнения. Теорема Виета. Рациональные уравнения. Решение задач, приводящих к квадратным и рациональным уравнениям. Основная цель – выработать умения решать квадратные уравнения, простейшие рациональные уравнения и уравнения, сводящиеся к квадратным, и применять их при решении задач. 4. Неравенства (26ч)Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Применение свойств неравенств к оценке значения выражения. Линейное неравенство с одной переменной. Система линейных неравенств с одной переменной. Основная цель – ознакомить учащихсяс применениемнеравенств для оценки значений выражений; выработать умение решать линейные неравенства с одной переменной и их системы. 5. Степень с целым показателем (18ч)Степень с целым показателем и ее свойства. Стандартный вид числа. Запись приближенных значений. Действия над приближенными значениями. Основная цель – сформировать умение выполнять действия над степенями с целыми показателями, ввести понятие стандартного вида числа. 6. Повторение. Решение задач (10ч).Учебно-тематический план
ТЕМАТИКА КОНТРОЛЬНЫХ РАБОТ
ЛИТЕРАТУРА
15. Для преподавателей. Поурочные планы по учебнику А.Г. Мордковича 8 класс. Е.А. Ким. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
 и ее график
и ее график